第九章 图形的相似 4 探索三角形相似的条件 第3课时 利用边的关系判定两个三角形相似(含答案)
文档属性
| 名称 | 第九章 图形的相似 4 探索三角形相似的条件 第3课时 利用边的关系判定两个三角形相似(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 479.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 12:49:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第3课时 利用边的关系判定两个三角形相似
轻松过关
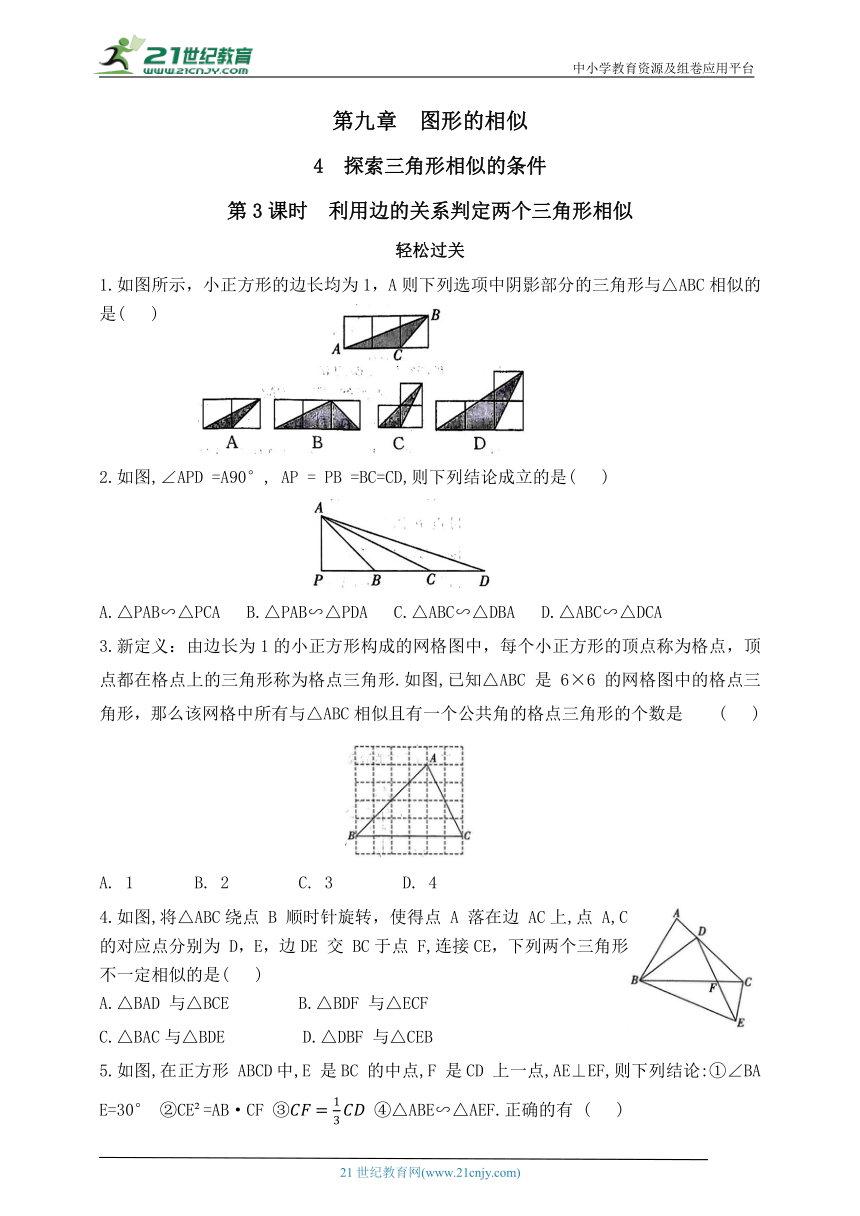
1.如图所示,小正方形的边长均为1,A则下列选项中阴影部分的三角形与△ABC相似的是( )
2.如图,∠APD =A90°, AP = PB =BC=CD,则下列结论成立的是( )
A.△PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D.△ABC∽△DCA
3.新定义:由边长为1的小正方形构成的网格图中,每个小正方形的顶点称为格点,顶点都在格点上的三角形称为格点三角形.如图,已知△ABC 是 6×6 的网格图中的格点三角形,那么该网格中所有与△ABC相似且有一个公共角的格点三角形的个数是 ( )
A. 1 B. 2 C. 3 D. 4
4.如图,将△ABC绕点 B 顺时针旋转,使得点 A 落在边 AC上,点 A,C的对应点分别为 D,E,边DE 交 BC于点 F,连接CE,下列两个三角形不一定相似的是( )
A.△BAD 与△BCE B.△BDF 与△ECF
C.△BAC与△BDE D.△DBF 与△CEB
5.如图,在正方形 ABCD中,E 是BC 的中点,F 是CD 上一点,AE⊥EF,则下列结论:①∠BAE=30° ②CE =AB·CF ④△ABE∽△AEF.正确的有 ( )
A. 1个 B.2 个 C.3个 D.4个
第5题图 第6题图
6.如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点 A,B,C,D,E中选取三个点所构成的三角形与△OPQ 相似,那么这个三角形是 .
7.下列论断:①顺次连接三角形各边的中点,所得的三角形与原三角形相似 ②两边长分别是3,4的Rt△ABC与两边长分别是6,8的Rt△DEF相似 ③若两个三角形的边长分别是4,6,8和6,8,10,则这两个三角形相似 ④一个三角形的三边长分别为6cm,9cm,7.5cm,另一个三角形的三边长分别为8cm,12cm,10cm,则这两个三角形相似.其中正确的有 .(填序号)
8.如图,在正方形网格上有6个斜三角形:①△ABC ②△CDB ③△DEB ④△FBG ⑤△HGF ⑥△EKF.在②~⑥中,所有与①相似的三角形的序号是 .
9.如图,已知一次函数 的图象与两坐标轴分别交于A,B,点C在x轴上,AC=4,第一象限内有一个点 P,且 PC⊥x轴于点 C,若以点 P,A,C为顶点的三角形与△OAB 相似,则点 P 的坐标为 .
第9题图 第10题图
10.如图,在边长为4 的正方形ABCD中,点 E,F分别是BC,CD的中点,DE,AF交于点G,AF的中点为H,连接BG,DH.给出下列结论:①AF⊥DE ③HD∥BG ④△ABG∽△DHF.其中正确的结论有 .(填序号)
11.如图, ,那么△ABD 与△BCE 相似吗 为什么
12.如图,点 B,D,E在一条直线上,BE与AC相交于点F,
(1)求证:∠BAD=∠CAE;
(2)若∠BAD=21°,求∠EBC的度数;
(3)连接EC,求证:△ABD∽△ACE.
快乐拓展
13.如图,在△ABC中,AB=3,AC=4,BC=6,D 是BC 上一点,CD=2,过点 D 的直线 将△ABC分成两部分,使其所分成的三角形与△ABC 相似,若直线与△ABC另一边的交点为点P,则 DP= .
14.如图,已知四边形 ABCD 是菱形,对角线AC,BD相交于点O,BD=2AC.过点 A作AE⊥CD,垂足为点 E,AE 与 BD 相交于点F.过点 C作CG⊥AC,与 AE 的延长线相交于点G.求证:
(1)△ACG≌△DOA;
(2)DF·BD=2DE·AG.
参考答案
1. A 2. C 3. D 4. D 5. B 6. △CDB
7.①④ 8.③④⑤ 9.(6,8)或(6,2) 10.①④
11.解:∵∴△ABC∽△DBE,∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE,
∴△ABD∽△CBE.
12.解:(1)证明: ∴△ABC∽△ADE;∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,即∠BAD=∠CAE;
(2)∵△ABC∽△ADE,∴∠ABC=∠ADE,
∵∠ABC =∠ABE+∠EBC,∠ADE =∠ABE+∠BAD,∴∠EBC=∠BAD=21°;
(3)证明:如图,
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
13.1或 或 解析:如图1,若DP∥AB,
∴△CDP∽△CBA,∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
14.证明:(1)∵四边形 ABCD 为菱形,∴AD=CD,AC⊥BD,OB=OD,
∴∠DAC=∠DCA,∠AOD=90°。
∵AE⊥CD,CG⊥AC,∴∠DCA+∠GCE=90°,∠G+∠GCE=90°,
∴∠G=∠DCA,∴∠G=∠DAC,
∵BD=2AC,BD=2OD,∴AC=OD,
在△ACG和△DOA中,∴△ACG≌△DOA(AAS);
(2)∵AE⊥CD,BD⊥AC,∴∠DOC=∠DEF=90°,
又∵∠CDO=∠FDE,∴△CDO∽△FDE,即OD·DF=DE·CD,
∵△ACG≌△DOA,∴AG=AD=CD,
又 ∴DF·BD=2DE·AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第3课时 利用边的关系判定两个三角形相似
轻松过关
1.如图所示,小正方形的边长均为1,A则下列选项中阴影部分的三角形与△ABC相似的是( )
2.如图,∠APD =A90°, AP = PB =BC=CD,则下列结论成立的是( )
A.△PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D.△ABC∽△DCA
3.新定义:由边长为1的小正方形构成的网格图中,每个小正方形的顶点称为格点,顶点都在格点上的三角形称为格点三角形.如图,已知△ABC 是 6×6 的网格图中的格点三角形,那么该网格中所有与△ABC相似且有一个公共角的格点三角形的个数是 ( )
A. 1 B. 2 C. 3 D. 4
4.如图,将△ABC绕点 B 顺时针旋转,使得点 A 落在边 AC上,点 A,C的对应点分别为 D,E,边DE 交 BC于点 F,连接CE,下列两个三角形不一定相似的是( )
A.△BAD 与△BCE B.△BDF 与△ECF
C.△BAC与△BDE D.△DBF 与△CEB
5.如图,在正方形 ABCD中,E 是BC 的中点,F 是CD 上一点,AE⊥EF,则下列结论:①∠BAE=30° ②CE =AB·CF ④△ABE∽△AEF.正确的有 ( )
A. 1个 B.2 个 C.3个 D.4个
第5题图 第6题图
6.如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点 A,B,C,D,E中选取三个点所构成的三角形与△OPQ 相似,那么这个三角形是 .
7.下列论断:①顺次连接三角形各边的中点,所得的三角形与原三角形相似 ②两边长分别是3,4的Rt△ABC与两边长分别是6,8的Rt△DEF相似 ③若两个三角形的边长分别是4,6,8和6,8,10,则这两个三角形相似 ④一个三角形的三边长分别为6cm,9cm,7.5cm,另一个三角形的三边长分别为8cm,12cm,10cm,则这两个三角形相似.其中正确的有 .(填序号)
8.如图,在正方形网格上有6个斜三角形:①△ABC ②△CDB ③△DEB ④△FBG ⑤△HGF ⑥△EKF.在②~⑥中,所有与①相似的三角形的序号是 .
9.如图,已知一次函数 的图象与两坐标轴分别交于A,B,点C在x轴上,AC=4,第一象限内有一个点 P,且 PC⊥x轴于点 C,若以点 P,A,C为顶点的三角形与△OAB 相似,则点 P 的坐标为 .
第9题图 第10题图
10.如图,在边长为4 的正方形ABCD中,点 E,F分别是BC,CD的中点,DE,AF交于点G,AF的中点为H,连接BG,DH.给出下列结论:①AF⊥DE ③HD∥BG ④△ABG∽△DHF.其中正确的结论有 .(填序号)
11.如图, ,那么△ABD 与△BCE 相似吗 为什么
12.如图,点 B,D,E在一条直线上,BE与AC相交于点F,
(1)求证:∠BAD=∠CAE;
(2)若∠BAD=21°,求∠EBC的度数;
(3)连接EC,求证:△ABD∽△ACE.
快乐拓展
13.如图,在△ABC中,AB=3,AC=4,BC=6,D 是BC 上一点,CD=2,过点 D 的直线 将△ABC分成两部分,使其所分成的三角形与△ABC 相似,若直线与△ABC另一边的交点为点P,则 DP= .
14.如图,已知四边形 ABCD 是菱形,对角线AC,BD相交于点O,BD=2AC.过点 A作AE⊥CD,垂足为点 E,AE 与 BD 相交于点F.过点 C作CG⊥AC,与 AE 的延长线相交于点G.求证:
(1)△ACG≌△DOA;
(2)DF·BD=2DE·AG.
参考答案
1. A 2. C 3. D 4. D 5. B 6. △CDB
7.①④ 8.③④⑤ 9.(6,8)或(6,2) 10.①④
11.解:∵∴△ABC∽△DBE,∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE,
∴△ABD∽△CBE.
12.解:(1)证明: ∴△ABC∽△ADE;∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,即∠BAD=∠CAE;
(2)∵△ABC∽△ADE,∴∠ABC=∠ADE,
∵∠ABC =∠ABE+∠EBC,∠ADE =∠ABE+∠BAD,∴∠EBC=∠BAD=21°;
(3)证明:如图,
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
13.1或 或 解析:如图1,若DP∥AB,
∴△CDP∽△CBA,∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
14.证明:(1)∵四边形 ABCD 为菱形,∴AD=CD,AC⊥BD,OB=OD,
∴∠DAC=∠DCA,∠AOD=90°。
∵AE⊥CD,CG⊥AC,∴∠DCA+∠GCE=90°,∠G+∠GCE=90°,
∴∠G=∠DCA,∴∠G=∠DAC,
∵BD=2AC,BD=2OD,∴AC=OD,
在△ACG和△DOA中,∴△ACG≌△DOA(AAS);
(2)∵AE⊥CD,BD⊥AC,∴∠DOC=∠DEF=90°,
又∵∠CDO=∠FDE,∴△CDO∽△FDE,即OD·DF=DE·CD,
∵△ACG≌△DOA,∴AG=AD=CD,
又 ∴DF·BD=2DE·AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
