第九章 图形的相似 5 相似三角形判定定理的证明
文档属性
| 名称 | 第九章 图形的相似 5 相似三角形判定定理的证明 |

|
|
| 格式 | docx | ||
| 文件大小 | 452.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 13:03:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
5 相似三角形判定定理的证明
轻松过关
1.如图,点 E 为矩形ABCD边CD 延长线上一点,BE 交 AD 于点 G,AF⊥BE 于点 F,则图中与△EDG 相似的三角形共有 ( )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图
2.如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE 的是 ( )
①∠C=∠E ②∠B=∠ADE
A.①②③ B.①②④ C.②③④ D.①②③④
3.如图,在 ABCD 中,F 是AD 上一点,CF 交 BD 于点 E,CF 的延长线交 BA 的延长线于点G,EF=1,EC=3,则 GF 的长为 ( )
A.4 B.6 C.8 D.10
第3题图 第4题图
4.如图,在钝角三角形 ABC中,AB=3c m,AC=6 cm,动点 D 从点 A 出发沿 AB以1 cm/s的速度向点 B 运动,同时动点 E 从点 C出发沿 CA 以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC 相似时,运动时间是 ( )
A.3s 或4.8s B. 3s C.4.5s D.1.5s 或2.4s
5.如图,在△ABC中,AB=5,AC=6,点 D 在边 AB 上,且AD=2,在AC上找一点E,使得B△ADE与原三角形相似,则AE的长是( )
A.2.4 B. C.2.4或 D.
6.如图,AB∥CD,AD,BC相交于点E,若AE:DE=1:2,AB=2.5,则CD的长为 .
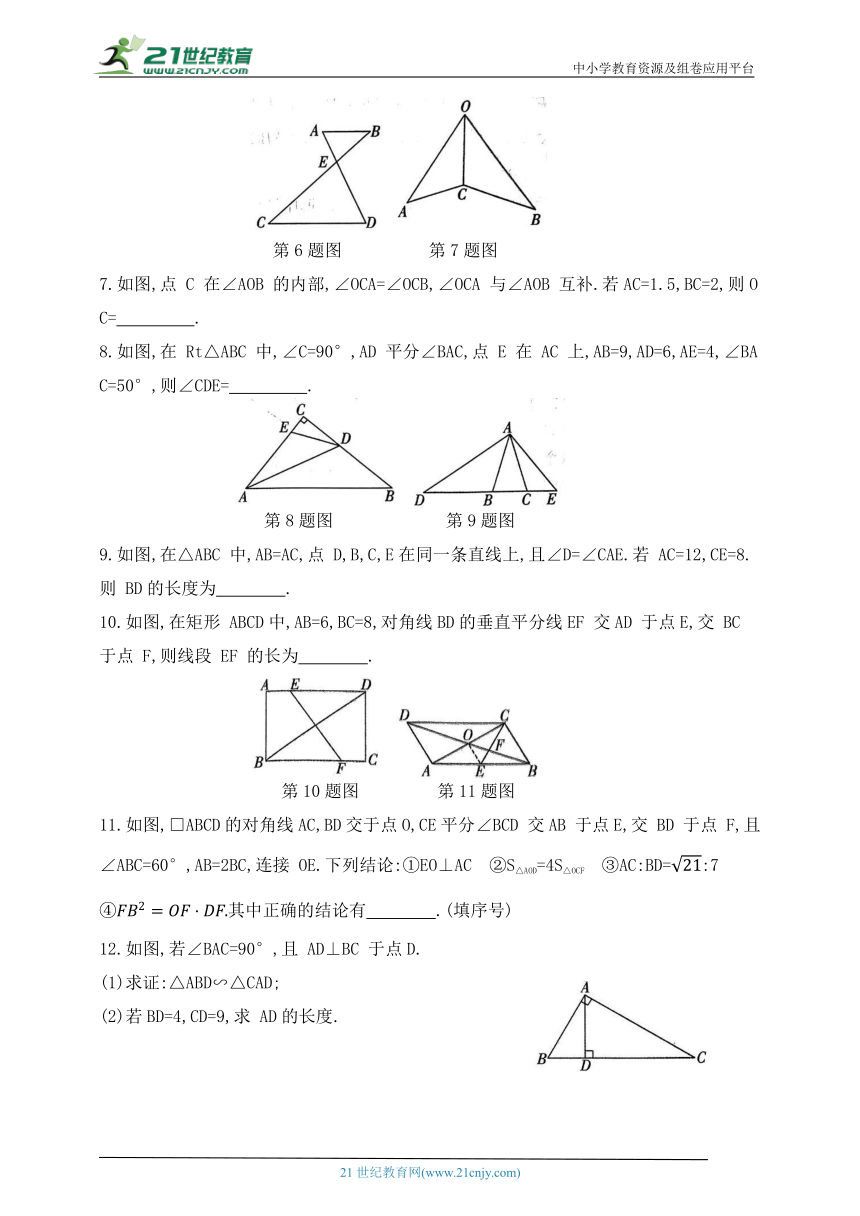
第6题图 第7题图
7.如图,点 C 在∠AOB 的内部,∠OCA=∠OCB,∠OCA 与∠AOB 互补.若AC=1.5,BC=2,则OC= .
8.如图,在 Rt△ABC 中,∠C=90°,AD 平分∠BAC,点 E 在 AC 上,AB=9,AD=6,AE=4,∠BAC=50°,则∠CDE= .
第8题图 第9题图
9.如图,在△ABC 中,AB=AC,点 D,B,C,E在同一条直线上,且∠D=∠CAE.若 AC=12,CE=8.则 BD的长度为 .
10.如图,在矩形 ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF 交AD 于点E,交 BC 于点 F,则线段 EF 的长为 .
第10题图 第11题图
11.如图,□ABCD的对角线AC,BD交于点O,CE平分∠BCD 交AB 于点E,交 BD 于点 F,且∠ABC=60°,AB=2BC,连接 OE.下列结论:①EO⊥AC ②S△AOD=4S△OCF ③AC:BD=:7 其中正确的结论有 .(填序号)
12.如图,若∠BAC=90°,且 AD⊥BC 于点D.
(1)求证:△ABD∽△CAD;
(2)若BD=4,CD=9,求 AD的长度.
13.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点 D,E,BE 交AD 于点 F,AB=AD.
(1)求证:△BFD∽△CAB;
(2)求证:AF=DF;
的值等于 .
14.如图,已知△ABC是边长为6 cm 的等边三角形,动点P,Q 同时从A,B两点出发,分别沿 AB,BC匀速运动,其中点 P 运动的速度是 1 cm/s,点 Q运动的速度是 2 cm/s,当点 Q 到达点 C时,P,Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)设△BPQ 的面积为 S(cm ),求 S 与t的函数关系式;
(2)作QR∥BA 交AC 于点R,连接PR,当t为何值时,△APR∽△PRQ
快乐拓展
15.如图1,先把一张矩形纸片 ABCD 难题选讲上下对折,设折痕为 MN;如图2,再把点 B 叠在折痕线上,得到△ABE,过点 B 向右折纸片,使 D,Q,A 三点仍保持在一条直线上,得折痕 PQ.
(1)求证:△PBE∽△QAB;
(2)你认为△PBE 和△BAE 相似吗 若相似,给出证明;若不相似,请说明理由;
(3)延长 EB 交 AD 于点 H,请直接写出△AEH 的形状为 .
参考答案
1. C 2. B 3. C 4. D 5. C
6.5 7. 8. 25° 9. 18 10. 11. ①③④
12.解:(1)证明:∵∠BAC=90°,AD⊥BC.∴∠ADB=90°,∠B+∠C=90°,
∴∠B+∠BAD=90°,∴∠BAD=∠C,
又∵∠ADB=∠CDA.∴△ABD∽△CAD;
(2)∵△ABD∽△CAD,
又∵BD=4,CD=9,∴AD =BD·CD=36.∴AD=6(负值已舍去).
13.解:(1)证明:∵DE垂直平分BC,∴BE=CE,∴∠C=∠EBD,
∵AB=AD,∴∠FDB=∠ABD,∴△BFD∽△CAB;
(2)证明:∵DE垂直平分BC,
∵△BFD∽△CAB,
∵AB=AD,∴AF=FD;
(3)如图,过点C作CH∥AD,交 BE的延长线于点 H,
∵DE垂直平分BC,
∵CH∥AD,∴∠BDF=∠BCH,∠BFD=∠BHC,
∴△BDF∽△BCH,
∵AF=FD,
∵AD∥HC,∴∠FAE=∠HCE,∠AFE=∠CHE,
∴△AFE∽△CHE,
∴FH=FB,故答案为:
14.解:(1)过点 Q作QE⊥AB,垂足为 E,
在 Rt△BEQ中, QB=2t,
∵AP=t,∴PB=6-t,
(2)∵QR∥BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,
又∵∠C=60°,∴△QRC是等边三角形,∴QR=RC=QC=6-2t,
由(1)得,BE=t,∴EP=AB-AP-BE=6-t-t=6-2t,
∴EP∥QR,EP=QR,∴四边形 EPRQ是平行四边形,
又∵∠PEQ=90°,∴∠APR=∠PRQ=90°,
∵△APR∽△PRQ,解得
∴当 时,△APR∽△PRQ.
15.解:(1)证明:∵∠PBE+∠ABQ= 90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.
在△PBE与△QAB中,∵∠ABQ= ∠PEB,∠BPE=∠AQB =90°,∴△PBE∽△QAB;
(2)△PBE和△BAE相似.∵△PBE∽△QAB,
∵BQ=PB,
又∵∠EPB=∠EBA=90°,∴△PBE∽△BAE;
(3)在△PBE和△QBH中,∴△PBE≌△QBH(ASA),∴BE=BH,
∵AB⊥EH,∴AE=AH,∠EAB=∠HAB=30°,∴∠EAH=60°,
∴△AEH是等边三角形;故答案为:等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
5 相似三角形判定定理的证明
轻松过关
1.如图,点 E 为矩形ABCD边CD 延长线上一点,BE 交 AD 于点 G,AF⊥BE 于点 F,则图中与△EDG 相似的三角形共有 ( )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图
2.如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE 的是 ( )
①∠C=∠E ②∠B=∠ADE
A.①②③ B.①②④ C.②③④ D.①②③④
3.如图,在 ABCD 中,F 是AD 上一点,CF 交 BD 于点 E,CF 的延长线交 BA 的延长线于点G,EF=1,EC=3,则 GF 的长为 ( )
A.4 B.6 C.8 D.10
第3题图 第4题图
4.如图,在钝角三角形 ABC中,AB=3c m,AC=6 cm,动点 D 从点 A 出发沿 AB以1 cm/s的速度向点 B 运动,同时动点 E 从点 C出发沿 CA 以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC 相似时,运动时间是 ( )
A.3s 或4.8s B. 3s C.4.5s D.1.5s 或2.4s
5.如图,在△ABC中,AB=5,AC=6,点 D 在边 AB 上,且AD=2,在AC上找一点E,使得B△ADE与原三角形相似,则AE的长是( )
A.2.4 B. C.2.4或 D.
6.如图,AB∥CD,AD,BC相交于点E,若AE:DE=1:2,AB=2.5,则CD的长为 .
第6题图 第7题图
7.如图,点 C 在∠AOB 的内部,∠OCA=∠OCB,∠OCA 与∠AOB 互补.若AC=1.5,BC=2,则OC= .
8.如图,在 Rt△ABC 中,∠C=90°,AD 平分∠BAC,点 E 在 AC 上,AB=9,AD=6,AE=4,∠BAC=50°,则∠CDE= .
第8题图 第9题图
9.如图,在△ABC 中,AB=AC,点 D,B,C,E在同一条直线上,且∠D=∠CAE.若 AC=12,CE=8.则 BD的长度为 .
10.如图,在矩形 ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF 交AD 于点E,交 BC 于点 F,则线段 EF 的长为 .
第10题图 第11题图
11.如图,□ABCD的对角线AC,BD交于点O,CE平分∠BCD 交AB 于点E,交 BD 于点 F,且∠ABC=60°,AB=2BC,连接 OE.下列结论:①EO⊥AC ②S△AOD=4S△OCF ③AC:BD=:7 其中正确的结论有 .(填序号)
12.如图,若∠BAC=90°,且 AD⊥BC 于点D.
(1)求证:△ABD∽△CAD;
(2)若BD=4,CD=9,求 AD的长度.
13.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点 D,E,BE 交AD 于点 F,AB=AD.
(1)求证:△BFD∽△CAB;
(2)求证:AF=DF;
的值等于 .
14.如图,已知△ABC是边长为6 cm 的等边三角形,动点P,Q 同时从A,B两点出发,分别沿 AB,BC匀速运动,其中点 P 运动的速度是 1 cm/s,点 Q运动的速度是 2 cm/s,当点 Q 到达点 C时,P,Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)设△BPQ 的面积为 S(cm ),求 S 与t的函数关系式;
(2)作QR∥BA 交AC 于点R,连接PR,当t为何值时,△APR∽△PRQ
快乐拓展
15.如图1,先把一张矩形纸片 ABCD 难题选讲上下对折,设折痕为 MN;如图2,再把点 B 叠在折痕线上,得到△ABE,过点 B 向右折纸片,使 D,Q,A 三点仍保持在一条直线上,得折痕 PQ.
(1)求证:△PBE∽△QAB;
(2)你认为△PBE 和△BAE 相似吗 若相似,给出证明;若不相似,请说明理由;
(3)延长 EB 交 AD 于点 H,请直接写出△AEH 的形状为 .
参考答案
1. C 2. B 3. C 4. D 5. C
6.5 7. 8. 25° 9. 18 10. 11. ①③④
12.解:(1)证明:∵∠BAC=90°,AD⊥BC.∴∠ADB=90°,∠B+∠C=90°,
∴∠B+∠BAD=90°,∴∠BAD=∠C,
又∵∠ADB=∠CDA.∴△ABD∽△CAD;
(2)∵△ABD∽△CAD,
又∵BD=4,CD=9,∴AD =BD·CD=36.∴AD=6(负值已舍去).
13.解:(1)证明:∵DE垂直平分BC,∴BE=CE,∴∠C=∠EBD,
∵AB=AD,∴∠FDB=∠ABD,∴△BFD∽△CAB;
(2)证明:∵DE垂直平分BC,
∵△BFD∽△CAB,
∵AB=AD,∴AF=FD;
(3)如图,过点C作CH∥AD,交 BE的延长线于点 H,
∵DE垂直平分BC,
∵CH∥AD,∴∠BDF=∠BCH,∠BFD=∠BHC,
∴△BDF∽△BCH,
∵AF=FD,
∵AD∥HC,∴∠FAE=∠HCE,∠AFE=∠CHE,
∴△AFE∽△CHE,
∴FH=FB,故答案为:
14.解:(1)过点 Q作QE⊥AB,垂足为 E,
在 Rt△BEQ中, QB=2t,
∵AP=t,∴PB=6-t,
(2)∵QR∥BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,
又∵∠C=60°,∴△QRC是等边三角形,∴QR=RC=QC=6-2t,
由(1)得,BE=t,∴EP=AB-AP-BE=6-t-t=6-2t,
∴EP∥QR,EP=QR,∴四边形 EPRQ是平行四边形,
又∵∠PEQ=90°,∴∠APR=∠PRQ=90°,
∵△APR∽△PRQ,解得
∴当 时,△APR∽△PRQ.
15.解:(1)证明:∵∠PBE+∠ABQ= 90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.
在△PBE与△QAB中,∵∠ABQ= ∠PEB,∠BPE=∠AQB =90°,∴△PBE∽△QAB;
(2)△PBE和△BAE相似.∵△PBE∽△QAB,
∵BQ=PB,
又∵∠EPB=∠EBA=90°,∴△PBE∽△BAE;
(3)在△PBE和△QBH中,∴△PBE≌△QBH(ASA),∴BE=BH,
∵AB⊥EH,∴AE=AH,∠EAB=∠HAB=30°,∴∠EAH=60°,
∴△AEH是等边三角形;故答案为:等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
