第九章 图形的相似 8 相似三角形的性质(含答案)
文档属性
| 名称 | 第九章 图形的相似 8 相似三角形的性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 506.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 12:56:17 | ||
图片预览

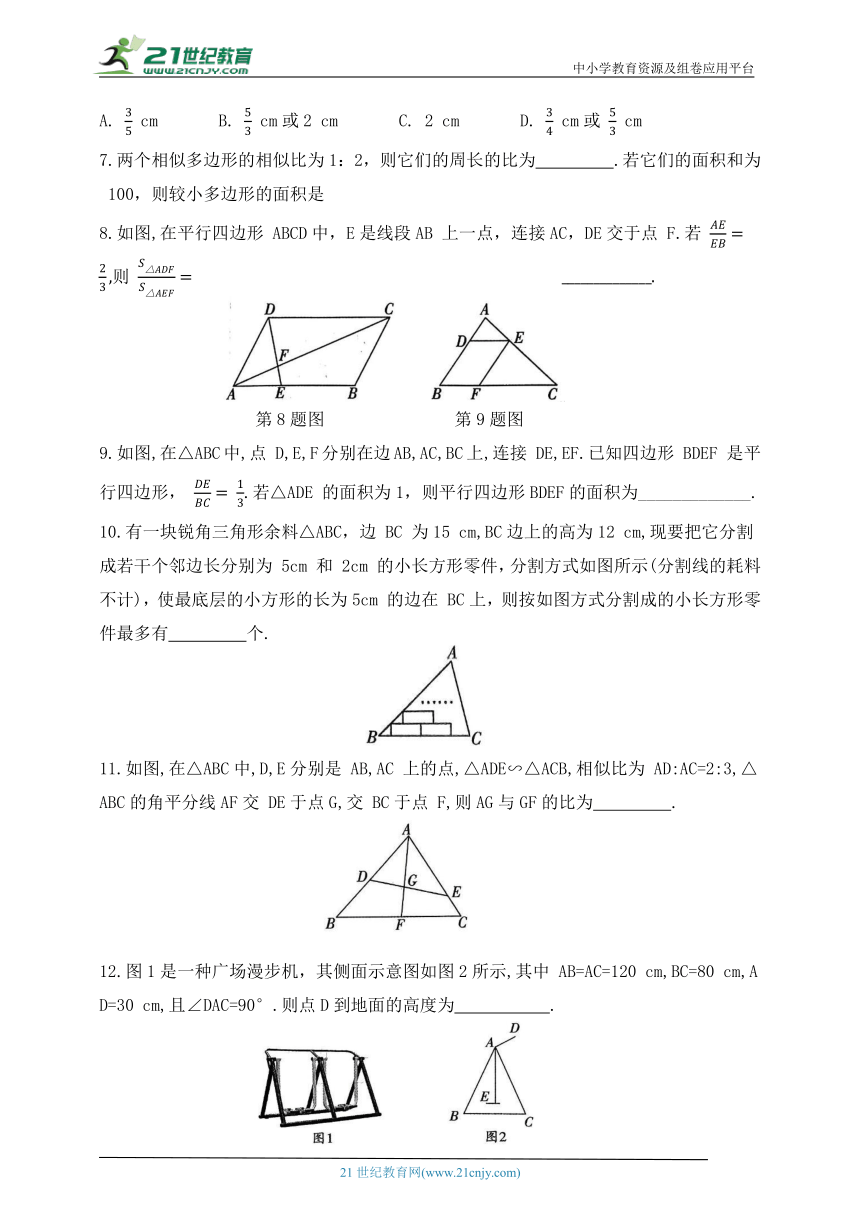


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
8 相似三角形的性质
轻松过关
1.如图,OA:OD=7:5,∠A=α,∠B=β,△OAB∽△ODC,△OAB与△OCD的面积分别是S 和S ,△OAB 与△OCD 的周长分别是C 和C ,则一定成立的等式是 ( )
2.两个相似多边形的面积比是 9 :25,若较小多边形的周长为6 cm,则较大多边形的周长为 ( )
A.16 cm C.10 cm D.25 cm
3.两个相似的五边形,如果一组对应边的长分别为 3c m,4 cm,且它们面积的差为28 cm ,则较大的五边形的面积为 ( )
A.44.8 cm C.64 cm D.54 cm
4.[2024·东坡模拟]如图,在△ABC 中,D 是边AB 上一点,按以下步骤作图:
①以点 A 为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;
②以点 D 为圆心,以AM长为半径作弧,交DB于点M';
③以点 M'为圆心,以MN 长为半径作弧,在∠BAC 内部交前面的弧于点 N';
④过点作射线交BC于点E.若△BDE与四边形 ACED 的面积比为9:40.则 的值为 ( )
A. B. C. D.
5.如图,在等腰三角形 ABC 中, AB =AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC 的面积为42,则四边形 DBCE 的面积是( )
A. 20 B. 22 C. 24 D. 26
6.在△ABC中,AB=6 cm,AC=5cm ,点 D,E分别在AB,AC上,△ADE 与△ABC 相似,且S△ADE : S四边形BCED =1 : 8,则 AD 的值为 ( )
A. cm B. cm或2 cm C. 2 cm D. cm或 cm
7.两个相似多边形的相似比为1:2,则它们的周长的比为 .若它们的面积和为 100,则较小多边形的面积是
8.如图,在平行四边形 ABCD中,E是线段AB 上一点,连接AC,DE交于点 F.若 则
第8题图 第9题图
9.如图,在△ABC中,点 D,E,F分别在边AB,AC,BC上,连接 DE,EF.已知四边形 BDEF 是平行四边形, .若△ADE 的面积为1,则平行四边形BDEF的面积为_____________.
10.有一块锐角三角形余料△ABC,边 BC 为15 cm,BC边上的高为12 cm,现要把它分割成若干个邻边长分别为 5cm 和 2cm 的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为5cm 的边在 BC上,则按如图方式分割成的小长方形零件最多有 个.
11.如图,在△ABC中,D,E分别是 AB,AC 上的点,△ADE∽△ACB,相似比为 AD:AC=2:3,△ABC的角平分线AF交 DE于点G,交 BC于点 F,则AG与GF的比为 .
12.图1是一种广场漫步机,其侧面示意图如图2所示,其中 AB=AC=120 cm,BC=80 cm,AD=30 cm,且∠DAC=90°.则点D到地面的高度为 .
13.如图,在△ABC中,点 D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设
①若BC=12,求线段 BE的长;
②若△EFC的面积是20,求△ABC 的面积.
14.如图是小红家阳台上晒衣架的横切面示意图,立杆AB,CD 相交于点O,B,D两点立于地面,经测量,AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm.现将晒衣架完全稳固张开,此时扣链 EF 成一条线段,且 EF=32 cm.若小红的连衣裙穿上衣架后的总长度达到 122 cm,问:垂挂在晒衣架上是否会拖落到地面 请通过计算说明理由.
15.如图,已知AB∥CD,且 试求△ABE与△DCE 的周长比与面积比.
16.如图,在△ABC中,D是BC 边上的中点,且 AD=AC,DE⊥BC,DE与AB 相交于点 E,EC与AD 相交于点F. BC=10,S△FCD=5.
(1)求证:△ABC∽△FCD;
(2)求 S△ABC;
(3)求 ED的长.
快乐拓展
17.如图,在矩形 ABCD中,AB=1,CB=2,连接AC,以对角线AC为边,按逆时针方向作矩形 ACC B ,使矩形 ACC B 相似于矩形 ABCD;再连接AC ,以对角线AC 为边,按逆时针方向作矩形 AC C B ,使矩形 AC C B 相似于矩
形……按照此规律作下去.若矩形ABCD的面积记作S ,矩形的面积记作 S ,矩形 AC C B 的面积记作S ,…,则的值为 .
18.如图1,一块材料的形状是锐角三角形ABC,边 BC=60,高AD=40.把它加工成正方形零件,使正方形的一边在 BC上,其余两个顶点分别在AB,AC上.
(1)计算出正方形零件的边长;
(2)如果要把△ABC按照图2加工成三个相同大小的正方形零件,求证:
(3)若△ABC可以按照图3加工成四个大小相同的正方形,且∠B=30°,求证:
参考答案
1. D 2. C 3. C 4. C 5. D 6. B
7.1:2 20 8. 9. 4 10. 6 11. 2:1
12.(10+80)cm 解析:如图,过点 A 作AF⊥BC 于点 F,过点 D 作 DH⊥AF,交FA的延长线于点H.
∵AB=AC,AF⊥BC,
在Rt△AFC中,
∴∠DAH+∠FAC=90°,
又∵∠C+∠FAC=90°.∴∠DAH=∠C.∴△DAH∽△ACF.
即 解得AH=10.
∴HF=AH+AF=(10+80 ) cm.
答:点D到地面的高度为(
13.解:(1)证明:∵DE∥AC,∴∠DEB=∠FCE,
∵EF∥AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;
(2)①∵EF∥AB,
∵EC=BC-BE=12-BE,解得 BE=4;
∵EF∥AB,∴△EFC∽△BAC,
14.解:小红的连衣裙会拖落到地面.理由如下:过点 O 作 OM⊥EF 于点 M,过点 A 作AH⊥BD于点H.
∵OE=OF,
易得EF∥BD,∴∠OEM=∠ABH.
又∵∠OME=∠AHB=90°,∴△OEM∽△ABH.
即 解得AH=120.
∵122>120,∴小红的连衣裙会拖落到地面.
15.解: 且两个三角形同高,
∵AB∥CD,∴△ABE∽△CDE,
16.解:(1)∵D是BC 边上的中点,DE⊥BC,∴BE=CE,∠B=∠ECD,
∵AD=AC,∴∠ADC=∠ACD,∴△ABC∽△FCD;
(2)∵△ABC∽△FCD,
∵BC=2DC,S△PCD=5,
即 S△ABC的值为20;
(3)作AM⊥CD于点M,交CE于点N,
∵△ABC∽△FCD,即AC=2DF,
∵AD=AC,∴AD=2DF,∴DF=AF,
∵DE∥AM,∴∠FED=∠FNA,
∵∠DFE=∠AFN,∴△FED≌△FNA(AAS),∴DE=AN,
∵AD=AC,AM⊥CD,∴DM=MC,∵MN∥DE,∴EN=NC,
设 MN=a,则 DE=AN=2a,AM=3a,
18.解:(1)如图 1,设正方形零件的边长为x mm,则KD=EF=x,AK=40-x,
∵EF∥BC,∴△AEF∽△ABC,
∵AD⊥BC,解得x=24.
∴正方形零件的边长为24 mm;
(2)证明:如图2,由已知,得EF∥GH∥BC,
在△GBN与△EGM中,∴△GBN≌△EGM(AAS),∴EG=BG,
∵△AEF∽△AGH,∴AE=EG,∴AE=EG=GB,
∵△AEF∽△ABC,
设EF=x,∴PD=2x,∴AD=3x,BC=3x,∴AD=BC;
(3)证明:如图3中,过点 A 作AD⊥BC于点D,分别交 EF,GH于点M,N,
设每个正方形的边长为a,
∵EF∥GH∥BC,∴△AEF∽△AGH∽△ABC,
解得AD=2.5a,BC=5a,∴BC=2AD.
∵∠B=30°,AD⊥BC,∴AB=2AD,∴AB=BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
8 相似三角形的性质
轻松过关
1.如图,OA:OD=7:5,∠A=α,∠B=β,△OAB∽△ODC,△OAB与△OCD的面积分别是S 和S ,△OAB 与△OCD 的周长分别是C 和C ,则一定成立的等式是 ( )
2.两个相似多边形的面积比是 9 :25,若较小多边形的周长为6 cm,则较大多边形的周长为 ( )
A.16 cm C.10 cm D.25 cm
3.两个相似的五边形,如果一组对应边的长分别为 3c m,4 cm,且它们面积的差为28 cm ,则较大的五边形的面积为 ( )
A.44.8 cm C.64 cm D.54 cm
4.[2024·东坡模拟]如图,在△ABC 中,D 是边AB 上一点,按以下步骤作图:
①以点 A 为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;
②以点 D 为圆心,以AM长为半径作弧,交DB于点M';
③以点 M'为圆心,以MN 长为半径作弧,在∠BAC 内部交前面的弧于点 N';
④过点作射线交BC于点E.若△BDE与四边形 ACED 的面积比为9:40.则 的值为 ( )
A. B. C. D.
5.如图,在等腰三角形 ABC 中, AB =AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC 的面积为42,则四边形 DBCE 的面积是( )
A. 20 B. 22 C. 24 D. 26
6.在△ABC中,AB=6 cm,AC=5cm ,点 D,E分别在AB,AC上,△ADE 与△ABC 相似,且S△ADE : S四边形BCED =1 : 8,则 AD 的值为 ( )
A. cm B. cm或2 cm C. 2 cm D. cm或 cm
7.两个相似多边形的相似比为1:2,则它们的周长的比为 .若它们的面积和为 100,则较小多边形的面积是
8.如图,在平行四边形 ABCD中,E是线段AB 上一点,连接AC,DE交于点 F.若 则
第8题图 第9题图
9.如图,在△ABC中,点 D,E,F分别在边AB,AC,BC上,连接 DE,EF.已知四边形 BDEF 是平行四边形, .若△ADE 的面积为1,则平行四边形BDEF的面积为_____________.
10.有一块锐角三角形余料△ABC,边 BC 为15 cm,BC边上的高为12 cm,现要把它分割成若干个邻边长分别为 5cm 和 2cm 的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为5cm 的边在 BC上,则按如图方式分割成的小长方形零件最多有 个.
11.如图,在△ABC中,D,E分别是 AB,AC 上的点,△ADE∽△ACB,相似比为 AD:AC=2:3,△ABC的角平分线AF交 DE于点G,交 BC于点 F,则AG与GF的比为 .
12.图1是一种广场漫步机,其侧面示意图如图2所示,其中 AB=AC=120 cm,BC=80 cm,AD=30 cm,且∠DAC=90°.则点D到地面的高度为 .
13.如图,在△ABC中,点 D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设
①若BC=12,求线段 BE的长;
②若△EFC的面积是20,求△ABC 的面积.
14.如图是小红家阳台上晒衣架的横切面示意图,立杆AB,CD 相交于点O,B,D两点立于地面,经测量,AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm.现将晒衣架完全稳固张开,此时扣链 EF 成一条线段,且 EF=32 cm.若小红的连衣裙穿上衣架后的总长度达到 122 cm,问:垂挂在晒衣架上是否会拖落到地面 请通过计算说明理由.
15.如图,已知AB∥CD,且 试求△ABE与△DCE 的周长比与面积比.
16.如图,在△ABC中,D是BC 边上的中点,且 AD=AC,DE⊥BC,DE与AB 相交于点 E,EC与AD 相交于点F. BC=10,S△FCD=5.
(1)求证:△ABC∽△FCD;
(2)求 S△ABC;
(3)求 ED的长.
快乐拓展
17.如图,在矩形 ABCD中,AB=1,CB=2,连接AC,以对角线AC为边,按逆时针方向作矩形 ACC B ,使矩形 ACC B 相似于矩形 ABCD;再连接AC ,以对角线AC 为边,按逆时针方向作矩形 AC C B ,使矩形 AC C B 相似于矩
形……按照此规律作下去.若矩形ABCD的面积记作S ,矩形的面积记作 S ,矩形 AC C B 的面积记作S ,…,则的值为 .
18.如图1,一块材料的形状是锐角三角形ABC,边 BC=60,高AD=40.把它加工成正方形零件,使正方形的一边在 BC上,其余两个顶点分别在AB,AC上.
(1)计算出正方形零件的边长;
(2)如果要把△ABC按照图2加工成三个相同大小的正方形零件,求证:
(3)若△ABC可以按照图3加工成四个大小相同的正方形,且∠B=30°,求证:
参考答案
1. D 2. C 3. C 4. C 5. D 6. B
7.1:2 20 8. 9. 4 10. 6 11. 2:1
12.(10+80)cm 解析:如图,过点 A 作AF⊥BC 于点 F,过点 D 作 DH⊥AF,交FA的延长线于点H.
∵AB=AC,AF⊥BC,
在Rt△AFC中,
∴∠DAH+∠FAC=90°,
又∵∠C+∠FAC=90°.∴∠DAH=∠C.∴△DAH∽△ACF.
即 解得AH=10.
∴HF=AH+AF=(10+80 ) cm.
答:点D到地面的高度为(
13.解:(1)证明:∵DE∥AC,∴∠DEB=∠FCE,
∵EF∥AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;
(2)①∵EF∥AB,
∵EC=BC-BE=12-BE,解得 BE=4;
∵EF∥AB,∴△EFC∽△BAC,
14.解:小红的连衣裙会拖落到地面.理由如下:过点 O 作 OM⊥EF 于点 M,过点 A 作AH⊥BD于点H.
∵OE=OF,
易得EF∥BD,∴∠OEM=∠ABH.
又∵∠OME=∠AHB=90°,∴△OEM∽△ABH.
即 解得AH=120.
∵122>120,∴小红的连衣裙会拖落到地面.
15.解: 且两个三角形同高,
∵AB∥CD,∴△ABE∽△CDE,
16.解:(1)∵D是BC 边上的中点,DE⊥BC,∴BE=CE,∠B=∠ECD,
∵AD=AC,∴∠ADC=∠ACD,∴△ABC∽△FCD;
(2)∵△ABC∽△FCD,
∵BC=2DC,S△PCD=5,
即 S△ABC的值为20;
(3)作AM⊥CD于点M,交CE于点N,
∵△ABC∽△FCD,即AC=2DF,
∵AD=AC,∴AD=2DF,∴DF=AF,
∵DE∥AM,∴∠FED=∠FNA,
∵∠DFE=∠AFN,∴△FED≌△FNA(AAS),∴DE=AN,
∵AD=AC,AM⊥CD,∴DM=MC,∵MN∥DE,∴EN=NC,
设 MN=a,则 DE=AN=2a,AM=3a,
18.解:(1)如图 1,设正方形零件的边长为x mm,则KD=EF=x,AK=40-x,
∵EF∥BC,∴△AEF∽△ABC,
∵AD⊥BC,解得x=24.
∴正方形零件的边长为24 mm;
(2)证明:如图2,由已知,得EF∥GH∥BC,
在△GBN与△EGM中,∴△GBN≌△EGM(AAS),∴EG=BG,
∵△AEF∽△AGH,∴AE=EG,∴AE=EG=GB,
∵△AEF∽△ABC,
设EF=x,∴PD=2x,∴AD=3x,BC=3x,∴AD=BC;
(3)证明:如图3中,过点 A 作AD⊥BC于点D,分别交 EF,GH于点M,N,
设每个正方形的边长为a,
∵EF∥GH∥BC,∴△AEF∽△AGH∽△ABC,
解得AD=2.5a,BC=5a,∴BC=2AD.
∵∠B=30°,AD⊥BC,∴AB=2AD,∴AB=BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
