第九章 图形的相似 章末突破(含答案)
文档属性
| 名称 | 第九章 图形的相似 章末突破(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 645.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
章末突破
考点一 成比例线段
1.如图为阿成调整他的计算机画面的分辨率时看到的选项,当他从建议选项1920×1080调整成1400×1050时,由于比例改变(1920:1080≠1400:1050),画面左右会出现黑色区域,当比例不变就不会有此问题.判断阿成将他的计算机画面分辨率从1920×1080调整成下列哪一种时,画面左右不会出现黑色区域 ( )
A.1680×1050 B.1600×900 C.1440×900 D.1280×1024
2.已知 则的值为 ( )
A. B. C.1 D.3
3.书画装裱,是指为书画配上衬纸、卷轴以便张贴、欣赏和收藏,是我国具有民族传统的一门特殊艺术.如图,一幅书画在装裱前的大小是1.2m×0.8m.装裱后,上、下、左、右边衬的宽度分别是 am,bm,cm,dm.若装裱后 AB与 AD的比是16:10,且a=b,c=d,c=2a,求四周边衬的宽度.
考点二 平行线分线段成比例定理
4.如图,直线AD,BC交于点O,AB∥EF∥CD,若AO=2,OF=1,FD=2,则的值为
第4题图 第5题图
5.一个三层折叠花架如图所示,已知 AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则 BF的长为 cm.
6.如图,AD 是△ABC 的中线,E 是线段AD上的一点,且AD=3AE,连接CE 并延长交AB 于点F
(1)求 的值;
(2)若AF=2cm,求AB的长.
考点三 相似多边形
7.下列说法错误的是 ( )
A.任意两个矩形都相似 B.任意两个正六边形都相似
C.任意两个正方形都相似 D.有一个角对应相等的菱形相似
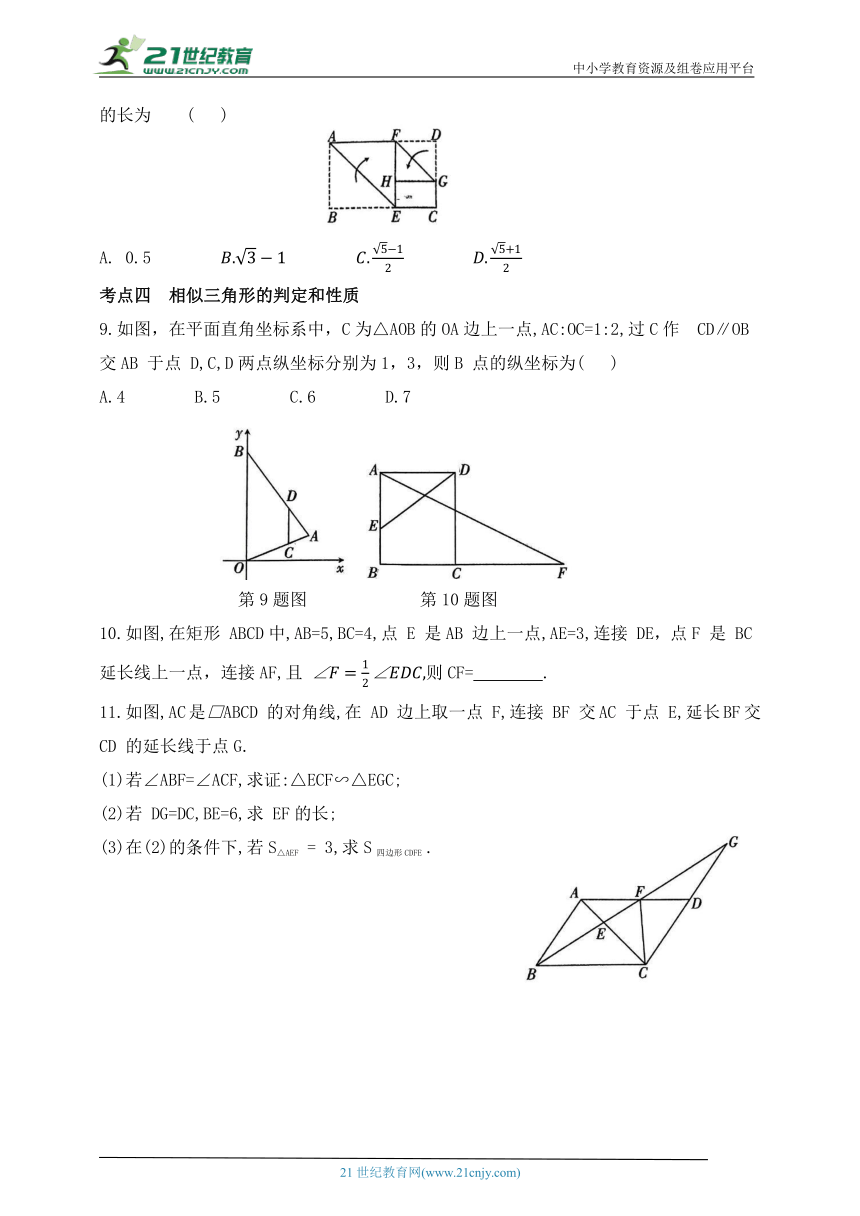
8.如图,四边形 ABCD 是一张矩形纸片.折叠该矩形纸片,使 AB 边落在 AD 边上,点B的对应点为点 F,折痕为 AE,展平后连接EF;继续折叠该纸片,使FD落在FE 上,点D 的对应点为点H,折痕为 FG,展平后连接 HG.若矩形HECG∽矩形 ABCD,AD=1,则 CD 的长为 ( )
A. 0.5
考点四 相似三角形的判定和性质
9.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC:OC=1:2,过C作 CD∥OB 交AB 于点 D,C,D两点纵坐标分别为1,3,则B 点的纵坐标为( )
A.4 B.5 C.6 D.7
第9题图 第10题图
10.如图,在矩形 ABCD中,AB=5,BC=4,点 E 是AB 边上一点,AE=3,连接 DE,点F 是 BC 延长线上一点,连接AF,且 则CF= .
11.如图,AC是□ABCD 的对角线,在 AD 边上取一点 F,连接 BF 交AC 于点 E,延长BF交CD 的延长线于点G.
(1)若∠ABF=∠ACF,求证:△ECF∽△EGC;
(2)若 DG=DC,BE=6,求 EF的长;
(3)在(2)的条件下,若S△AEF = 3,求S四边形CDFE .
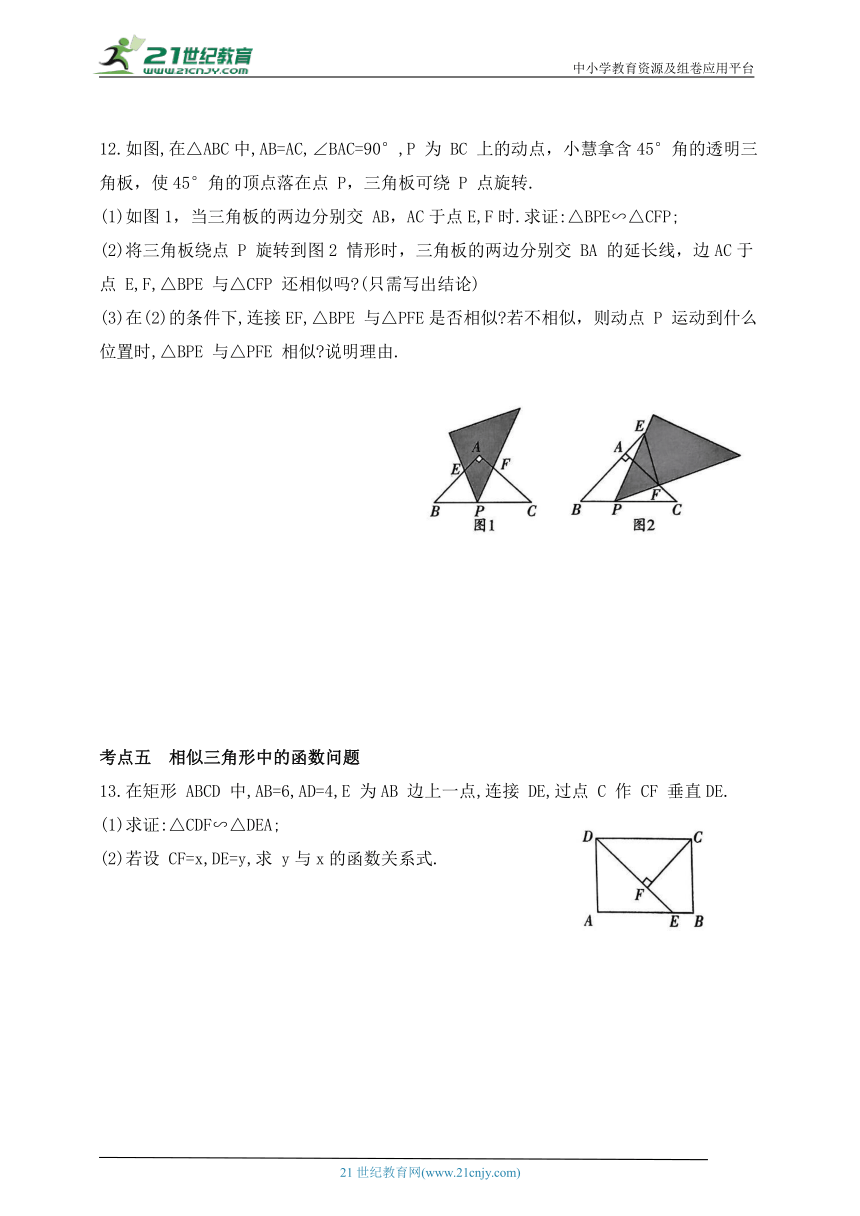
12.如图,在△ABC中,AB=AC,∠BAC=90°,P 为 BC 上的动点,小慧拿含45°角的透明三角板,使45°角的顶点落在点 P,三角板可绕 P 点旋转.
(1)如图1,当三角板的两边分别交 AB,AC于点E,F时.求证:△BPE∽△CFP;
(2)将三角板绕点 P 旋转到图2 情形时,三角板的两边分别交 BA 的延长线,边AC于点 E,F,△BPE 与△CFP 还相似吗 (只需写出结论)
(3)在(2)的条件下,连接EF,△BPE 与△PFE是否相似 若不相似,则动点 P 运动到什么位置时,△BPE 与△PFE 相似 说明理由.
考点五 相似三角形中的函数问题
13.在矩形 ABCD 中,AB=6,AD=4,E 为AB 边上一点,连接 DE,过点 C 作 CF 垂直DE.
(1)求证:△CDF∽△DEA;
(2)若设 CF=x,DE=y,求 y与x的函数关系式.
考点六 相似三角形中的分类讨论问题
14.如图,在Rt△ABC中,∠A=90°,点M,N分别为AB,AC上一个动点,以MN为对称轴将△AMN 折叠得到△DMN,点A的对应点为D,若点D落在BC上,且△AMN与 △ABC相似,已知AC=6,AB=8,求CD的长.
考点七 相似三角形中的动点问题
15. 如图,AB⊥BD,CD⊥BD,AB=5,CD=4,BD=12.点 P在 BD 上移动:当以 P,C,D为顶点的三角形与△ABP 相似时,则 PB的长为 .
第15题图 第16题图
16. 如图,在 ABCD 中 AB =3 cm,BC=6 cm.动点 E 从点 A 出发,以 2cm /s的速度向点 D 运动,运动到点 D 停止;动点 F同时从点C 出发,以1cm/s的速度向点 B运动,当点 E 停止运动时,点F 也随之停止运动.若△ABE 与△FCD 相似,则 t 的值为
考点八 黄金分割
17.如图,在△ABC 中,AB=AC,∠BAC=36°,以点 C 为圆心,以 BC为半径作弧交AC 于点 D,再分别以 B,D为圆心,以大于 BD的长为半径作弧,两弧相交于点 P,作射线 CP 交AB 于点E,连接DE.以下结论不正确的是 ( )
A.∠BCE=36° B. BC=AE
18.宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形 ABCD 是黄金矩形(ABA. 3 B. 2 C. 1 D. 0
考点九 相似三角形的实际应用
19.如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 A、镜子O、树底 B 三点在同一水平线上,眼睛与地面的高度为1.6米,OA=2.4米,OB=6米,则树高为 .
20.(1)如图1:小明想测量一棵树的高度 AB,在阳光下,小明测得一根与地面垂直、长为1 米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长 CD 为1.5米,落在地面上的影长 BC为3米,则树高 AB 为多少米 (2)如图2:在阳光下,小明在某一时刻测得与地面垂直、长为1m 的杆子在地面上的影子长为2m ,在斜坡上影长为1.5m ,他想测量电线杆 AB 的高度,但其影子恰好落在土坡的坡面 CD 和地面 BC 上,量得CD=3m,BC=10m,求电线杆的高度.
考点十 利用位似放缩图形
21.如图,在平面直角坐标系中,△ABC与△A'B'C'是位似图形,位似中心为点 O.若点 A(-3,1)的对应点为 则点 B(-2,4)的对应点B'的坐标为 ( )
A.(-4,8) B.(8,-4) C.(-8,4) D.(4,-8)
22.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为点
.
(1)把△ABC 先向右平移2个单位长度,再向下平移 3 个单位长度得到,并写出点 C 的坐标;
(2)以点 O为位似中心,将△A B C 放大两倍得到△A'B'C';
(3)直接写出△ABC的面积: .
易错点 位似变换因考虑不周全而漏解
23.如图,正方形网格中有一条简笔画“鱼”,请你以点 D 为位似中心将其放大,使新图形与原图形的对应线段的比是2:1,画出符合条件的所有图形.(不要求写作法)
参考答案
1. B 2. D
3.解:由题意,得AB=(1.2+c+d)m,AD=(0.8+a+b)m,
∵a=b,c=d,c=2a,∴AB=(1.2+c+d)m=(1.2+4a)m,AD=(0.8+a+b)m=(0.8+2a)m,
∵AB与AD的比是16:10,
∴(1.2+4a):(0.8+2a)=16:10,∴a=0.1,∴b=0.1,c=d=0.2,
答:上、下、左、右边衬的宽度分别是0.1m,0. 1m,0. 2m,0.2m.
4. 5.120
6.解:(1)∵AD=3AE,AD=AE+DE,∴3AE=AE+DE,
∴2AE=DE,
(2)如图,过点 D作DM∥CF交AB 于点M,
∵AD是△ABC的中线,∴BD=DC,∴BM=MF,
∵DM∥EF,
∵AF=2cm,∴FM=BM=4 cm,∴AB=AF+MF+BM=10 cm.
7. A 8. C 9. C 10.6
11.解:(1)证明:∵AB∥CG,∴∠ABF=∠G.
又∵∠ABF=∠ACF,∴∠ECF=∠G.
又∵∠CEF=∠CEG,∴△ECF∽△EGC;
(2)∵四边形 ABCD 是平行四边形,∴AB=CD.
∵DG=DC,∴AB=CD=DG,∴AB:CG=1:2.
∵AB∥CG,即 ∴EG=12,BG=18.
∵AB∥DG,
∴EF=BF-BE=9-6=3;
(3)过点 A 作AM⊥BG 于点 M,过点 C作CN⊥BG于点N.
∵AB∥CG,∴△ABE∽△CGE,
∵S△AEF=3,EF=3,∴AM=2,∴CN=4,
∵∠ABF=∠G,∠AFB=∠DFG,AB=CD=DG,∴△ABF≌△DGF(AAS),
∴S四边形CDFE=S△CDF+S△CEF=9+6=15.
12.解:(1)证明:∵在△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,∴∠BPE+∠BEP=135°,
∵∠EPF=45°,又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,∴∠BEP=∠CPF,
又∵∠B=∠C,∴△BPE∽△CFP;
(2)△BPE∽△CFP;
理由:∵在△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,∴∠BPE+∠BEP=135°,
∵∠EPF=45°,又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,∴∠BEP=∠CPF,
又∵∠B=∠C;∴△BPE∽△CFP;
(3)不相似.动点 P 运动到BC 中点位置时,△BPE与△PFE相似,
理由:同(1),得△BPE∽△CFP,∴CP:BE=PF:PE,又∵CP=BP,
∴PB:BE=PF:PE,
又∵∠EBP=∠EPF,∴△BPE∽△PFE.
13.解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,AB=CD.
∵CF垂直DE,∴∠CFD=90°.∴∠CFD=∠A.
∵∠DCF + ∠CDF = 90°, ∠ADE + ∴∠DCF=∠ADE.
∴△CDF∽△DEA;
(2)∵△CDF∽△DEA,
14.解:在 Rt△ABC中,AC=6,AB=8,由勾股定理,得.
∵△AMN 与△ABC相似,∴有以下两种情况:
①当∠ANM=∠C时,△AMN∽△ABC,连接AD,如图1所示:
∴MN∥BC,
由折叠,得MN⊥AD,∴AD⊥BC,∴∠ADC=∠BAC=90°,
又∵∠C=∠C,∴△ADC∽△BAC,
∴CD:AC=AC:BC,即CD:6=6:10,
②当∠ANM=∠B 时,△AMN∽△ACB,连接AD,如图2所示:
则∠AMN=∠C,
由折叠,得MN⊥AD,∴∠ANM+∠NAD=90°,
∵∠CAB=90°,∴∠NAD+∠DAB=90°,∴∠ANM=∠DAB,
又∵∠ANM=∠B,∴∠DAB=∠B,∴AD=BD,
同理,得∠DAC=∠C,∴CD=AD
综上所述,CD的长为 或5.
15.或2或10 17. C 18. D 19.4米
20.解:(1)设从墙上的影子的顶端到树的顶端的垂直高度是x米.
由题意,得 解得x=3.75.
∴树高是3.75+1.5=5.25(米),答:树高为5.25米;
(2)作CE∥AD交AB于点E.
∴AE=2,
∴BE=5,
∴AB=AE+BE=2+5=7(m),故电线杆的高度是7 m.
21. A
22.解:(1)如图,△A B C 即为所求作;点C 的坐标为(2,0);
(2)如图,△A'B'C'和△A'B'C'即为所求作;
故答案为:7.
23.解:如图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
章末突破
考点一 成比例线段
1.如图为阿成调整他的计算机画面的分辨率时看到的选项,当他从建议选项1920×1080调整成1400×1050时,由于比例改变(1920:1080≠1400:1050),画面左右会出现黑色区域,当比例不变就不会有此问题.判断阿成将他的计算机画面分辨率从1920×1080调整成下列哪一种时,画面左右不会出现黑色区域 ( )
A.1680×1050 B.1600×900 C.1440×900 D.1280×1024
2.已知 则的值为 ( )
A. B. C.1 D.3
3.书画装裱,是指为书画配上衬纸、卷轴以便张贴、欣赏和收藏,是我国具有民族传统的一门特殊艺术.如图,一幅书画在装裱前的大小是1.2m×0.8m.装裱后,上、下、左、右边衬的宽度分别是 am,bm,cm,dm.若装裱后 AB与 AD的比是16:10,且a=b,c=d,c=2a,求四周边衬的宽度.
考点二 平行线分线段成比例定理
4.如图,直线AD,BC交于点O,AB∥EF∥CD,若AO=2,OF=1,FD=2,则的值为
第4题图 第5题图
5.一个三层折叠花架如图所示,已知 AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则 BF的长为 cm.
6.如图,AD 是△ABC 的中线,E 是线段AD上的一点,且AD=3AE,连接CE 并延长交AB 于点F
(1)求 的值;
(2)若AF=2cm,求AB的长.
考点三 相似多边形
7.下列说法错误的是 ( )
A.任意两个矩形都相似 B.任意两个正六边形都相似
C.任意两个正方形都相似 D.有一个角对应相等的菱形相似
8.如图,四边形 ABCD 是一张矩形纸片.折叠该矩形纸片,使 AB 边落在 AD 边上,点B的对应点为点 F,折痕为 AE,展平后连接EF;继续折叠该纸片,使FD落在FE 上,点D 的对应点为点H,折痕为 FG,展平后连接 HG.若矩形HECG∽矩形 ABCD,AD=1,则 CD 的长为 ( )
A. 0.5
考点四 相似三角形的判定和性质
9.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC:OC=1:2,过C作 CD∥OB 交AB 于点 D,C,D两点纵坐标分别为1,3,则B 点的纵坐标为( )
A.4 B.5 C.6 D.7
第9题图 第10题图
10.如图,在矩形 ABCD中,AB=5,BC=4,点 E 是AB 边上一点,AE=3,连接 DE,点F 是 BC 延长线上一点,连接AF,且 则CF= .
11.如图,AC是□ABCD 的对角线,在 AD 边上取一点 F,连接 BF 交AC 于点 E,延长BF交CD 的延长线于点G.
(1)若∠ABF=∠ACF,求证:△ECF∽△EGC;
(2)若 DG=DC,BE=6,求 EF的长;
(3)在(2)的条件下,若S△AEF = 3,求S四边形CDFE .
12.如图,在△ABC中,AB=AC,∠BAC=90°,P 为 BC 上的动点,小慧拿含45°角的透明三角板,使45°角的顶点落在点 P,三角板可绕 P 点旋转.
(1)如图1,当三角板的两边分别交 AB,AC于点E,F时.求证:△BPE∽△CFP;
(2)将三角板绕点 P 旋转到图2 情形时,三角板的两边分别交 BA 的延长线,边AC于点 E,F,△BPE 与△CFP 还相似吗 (只需写出结论)
(3)在(2)的条件下,连接EF,△BPE 与△PFE是否相似 若不相似,则动点 P 运动到什么位置时,△BPE 与△PFE 相似 说明理由.
考点五 相似三角形中的函数问题
13.在矩形 ABCD 中,AB=6,AD=4,E 为AB 边上一点,连接 DE,过点 C 作 CF 垂直DE.
(1)求证:△CDF∽△DEA;
(2)若设 CF=x,DE=y,求 y与x的函数关系式.
考点六 相似三角形中的分类讨论问题
14.如图,在Rt△ABC中,∠A=90°,点M,N分别为AB,AC上一个动点,以MN为对称轴将△AMN 折叠得到△DMN,点A的对应点为D,若点D落在BC上,且△AMN与 △ABC相似,已知AC=6,AB=8,求CD的长.
考点七 相似三角形中的动点问题
15. 如图,AB⊥BD,CD⊥BD,AB=5,CD=4,BD=12.点 P在 BD 上移动:当以 P,C,D为顶点的三角形与△ABP 相似时,则 PB的长为 .
第15题图 第16题图
16. 如图,在 ABCD 中 AB =3 cm,BC=6 cm.动点 E 从点 A 出发,以 2cm /s的速度向点 D 运动,运动到点 D 停止;动点 F同时从点C 出发,以1cm/s的速度向点 B运动,当点 E 停止运动时,点F 也随之停止运动.若△ABE 与△FCD 相似,则 t 的值为
考点八 黄金分割
17.如图,在△ABC 中,AB=AC,∠BAC=36°,以点 C 为圆心,以 BC为半径作弧交AC 于点 D,再分别以 B,D为圆心,以大于 BD的长为半径作弧,两弧相交于点 P,作射线 CP 交AB 于点E,连接DE.以下结论不正确的是 ( )
A.∠BCE=36° B. BC=AE
18.宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形 ABCD 是黄金矩形(AB
考点九 相似三角形的实际应用
19.如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 A、镜子O、树底 B 三点在同一水平线上,眼睛与地面的高度为1.6米,OA=2.4米,OB=6米,则树高为 .
20.(1)如图1:小明想测量一棵树的高度 AB,在阳光下,小明测得一根与地面垂直、长为1 米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长 CD 为1.5米,落在地面上的影长 BC为3米,则树高 AB 为多少米 (2)如图2:在阳光下,小明在某一时刻测得与地面垂直、长为1m 的杆子在地面上的影子长为2m ,在斜坡上影长为1.5m ,他想测量电线杆 AB 的高度,但其影子恰好落在土坡的坡面 CD 和地面 BC 上,量得CD=3m,BC=10m,求电线杆的高度.
考点十 利用位似放缩图形
21.如图,在平面直角坐标系中,△ABC与△A'B'C'是位似图形,位似中心为点 O.若点 A(-3,1)的对应点为 则点 B(-2,4)的对应点B'的坐标为 ( )
A.(-4,8) B.(8,-4) C.(-8,4) D.(4,-8)
22.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为点
.
(1)把△ABC 先向右平移2个单位长度,再向下平移 3 个单位长度得到,并写出点 C 的坐标;
(2)以点 O为位似中心,将△A B C 放大两倍得到△A'B'C';
(3)直接写出△ABC的面积: .
易错点 位似变换因考虑不周全而漏解
23.如图,正方形网格中有一条简笔画“鱼”,请你以点 D 为位似中心将其放大,使新图形与原图形的对应线段的比是2:1,画出符合条件的所有图形.(不要求写作法)
参考答案
1. B 2. D
3.解:由题意,得AB=(1.2+c+d)m,AD=(0.8+a+b)m,
∵a=b,c=d,c=2a,∴AB=(1.2+c+d)m=(1.2+4a)m,AD=(0.8+a+b)m=(0.8+2a)m,
∵AB与AD的比是16:10,
∴(1.2+4a):(0.8+2a)=16:10,∴a=0.1,∴b=0.1,c=d=0.2,
答:上、下、左、右边衬的宽度分别是0.1m,0. 1m,0. 2m,0.2m.
4. 5.120
6.解:(1)∵AD=3AE,AD=AE+DE,∴3AE=AE+DE,
∴2AE=DE,
(2)如图,过点 D作DM∥CF交AB 于点M,
∵AD是△ABC的中线,∴BD=DC,∴BM=MF,
∵DM∥EF,
∵AF=2cm,∴FM=BM=4 cm,∴AB=AF+MF+BM=10 cm.
7. A 8. C 9. C 10.6
11.解:(1)证明:∵AB∥CG,∴∠ABF=∠G.
又∵∠ABF=∠ACF,∴∠ECF=∠G.
又∵∠CEF=∠CEG,∴△ECF∽△EGC;
(2)∵四边形 ABCD 是平行四边形,∴AB=CD.
∵DG=DC,∴AB=CD=DG,∴AB:CG=1:2.
∵AB∥CG,即 ∴EG=12,BG=18.
∵AB∥DG,
∴EF=BF-BE=9-6=3;
(3)过点 A 作AM⊥BG 于点 M,过点 C作CN⊥BG于点N.
∵AB∥CG,∴△ABE∽△CGE,
∵S△AEF=3,EF=3,∴AM=2,∴CN=4,
∵∠ABF=∠G,∠AFB=∠DFG,AB=CD=DG,∴△ABF≌△DGF(AAS),
∴S四边形CDFE=S△CDF+S△CEF=9+6=15.
12.解:(1)证明:∵在△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,∴∠BPE+∠BEP=135°,
∵∠EPF=45°,又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,∴∠BEP=∠CPF,
又∵∠B=∠C,∴△BPE∽△CFP;
(2)△BPE∽△CFP;
理由:∵在△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,∴∠BPE+∠BEP=135°,
∵∠EPF=45°,又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,∴∠BEP=∠CPF,
又∵∠B=∠C;∴△BPE∽△CFP;
(3)不相似.动点 P 运动到BC 中点位置时,△BPE与△PFE相似,
理由:同(1),得△BPE∽△CFP,∴CP:BE=PF:PE,又∵CP=BP,
∴PB:BE=PF:PE,
又∵∠EBP=∠EPF,∴△BPE∽△PFE.
13.解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,AB=CD.
∵CF垂直DE,∴∠CFD=90°.∴∠CFD=∠A.
∵∠DCF + ∠CDF = 90°, ∠ADE + ∴∠DCF=∠ADE.
∴△CDF∽△DEA;
(2)∵△CDF∽△DEA,
14.解:在 Rt△ABC中,AC=6,AB=8,由勾股定理,得.
∵△AMN 与△ABC相似,∴有以下两种情况:
①当∠ANM=∠C时,△AMN∽△ABC,连接AD,如图1所示:
∴MN∥BC,
由折叠,得MN⊥AD,∴AD⊥BC,∴∠ADC=∠BAC=90°,
又∵∠C=∠C,∴△ADC∽△BAC,
∴CD:AC=AC:BC,即CD:6=6:10,
②当∠ANM=∠B 时,△AMN∽△ACB,连接AD,如图2所示:
则∠AMN=∠C,
由折叠,得MN⊥AD,∴∠ANM+∠NAD=90°,
∵∠CAB=90°,∴∠NAD+∠DAB=90°,∴∠ANM=∠DAB,
又∵∠ANM=∠B,∴∠DAB=∠B,∴AD=BD,
同理,得∠DAC=∠C,∴CD=AD
综上所述,CD的长为 或5.
15.或2或10 17. C 18. D 19.4米
20.解:(1)设从墙上的影子的顶端到树的顶端的垂直高度是x米.
由题意,得 解得x=3.75.
∴树高是3.75+1.5=5.25(米),答:树高为5.25米;
(2)作CE∥AD交AB于点E.
∴AE=2,
∴BE=5,
∴AB=AE+BE=2+5=7(m),故电线杆的高度是7 m.
21. A
22.解:(1)如图,△A B C 即为所求作;点C 的坐标为(2,0);
(2)如图,△A'B'C'和△A'B'C'即为所求作;
故答案为:7.
23.解:如图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
