2025年九年级中考数学三轮冲刺训练四边形压轴题训练(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练四边形压轴题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 16:16:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练四边形压轴题训练
1.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=10cm,BD=4cm.动点P从点A出发,沿AB方向匀速运动,速度为1cm/s;同时,动点Q从点A出发,沿AD方向匀速运动,速度为2cm/s.以AP,AQ为邻边的平行四边形APMQ的边PM与AC交于点E.设运动时间为t(s)(0<t≤5),解答下列问题:
(1)当点M在BD上时,求t的值;
(2)连接BE.设△PEB的面积为S(cm2),求S与t的函数关系式和S的最大值;
(3)是否存在某一时刻t,使点B在∠PEC的平分线上?若存在,求出t的值;若不存在,请说明理由.
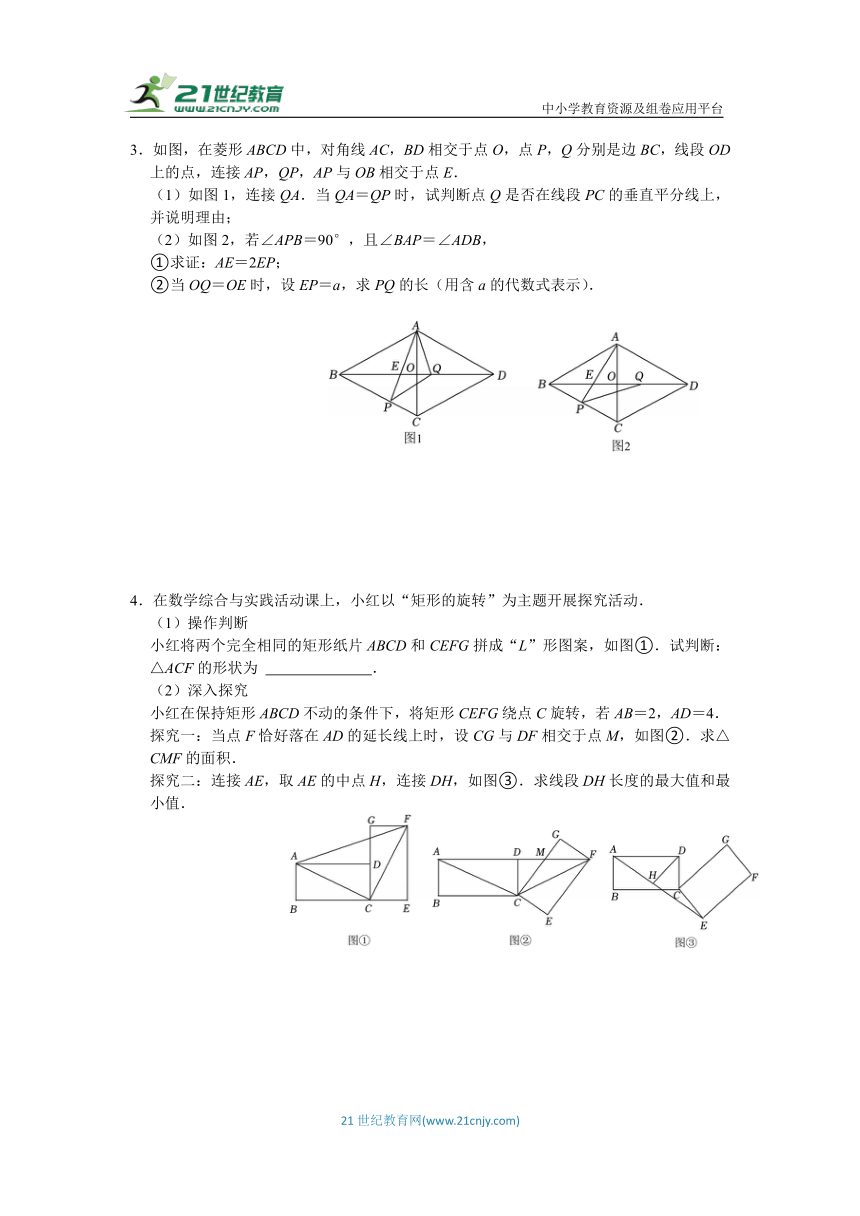
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
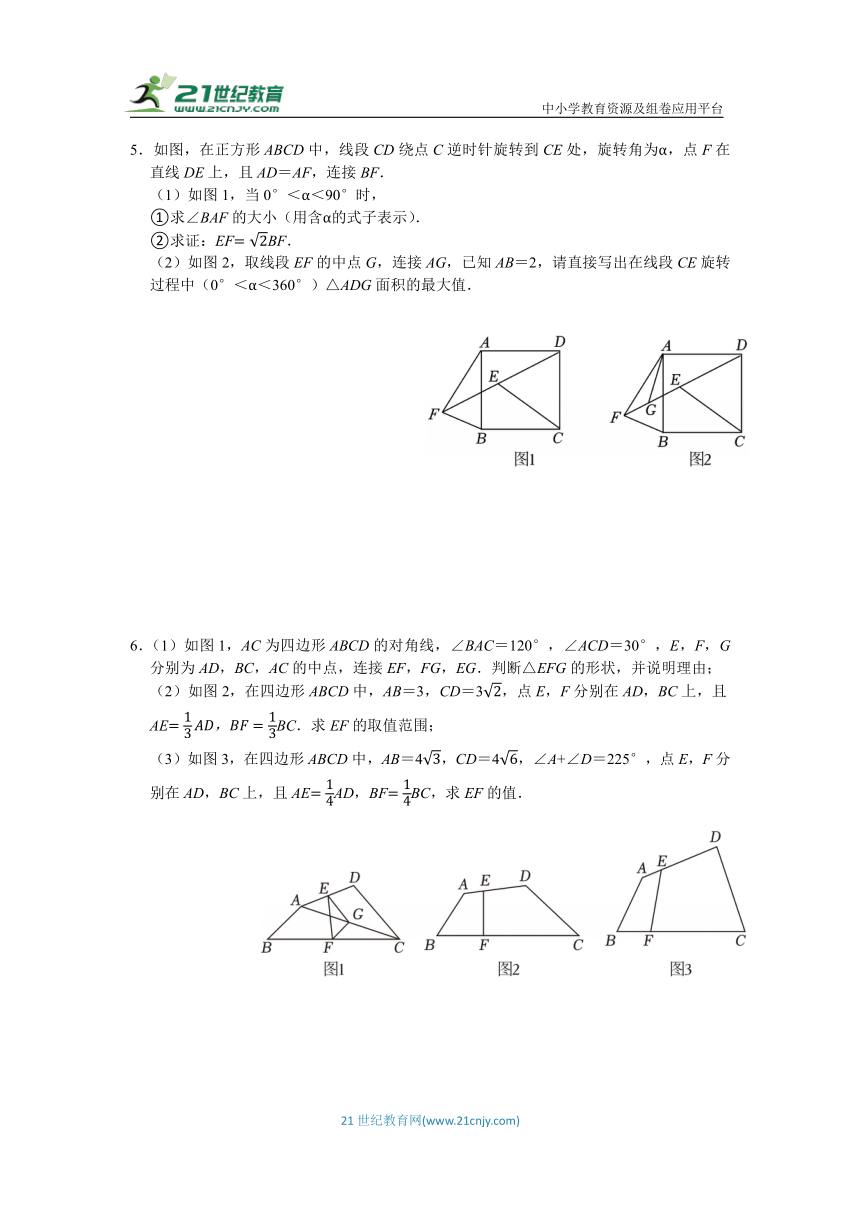
4.在数学综合与实践活动课上,小红以“矩形的旋转”为主题开展探究活动.
(1)操作判断
小红将两个完全相同的矩形纸片ABCD和CEFG拼成“L”形图案,如图①.试判断:△ACF的形状为 .
(2)深入探究
小红在保持矩形ABCD不动的条件下,将矩形CEFG绕点C旋转,若AB=2,AD=4.
探究一:当点F恰好落在AD的延长线上时,设CG与DF相交于点M,如图②.求△CMF的面积.
探究二:连接AE,取AE的中点H,连接DH,如图③.求线段DH长度的最大值和最小值.
5.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
6.(1)如图1,AC为四边形ABCD的对角线,∠BAC=120°,∠ACD=30°,E,F,G分别为AD,BC,AC的中点,连接EF,FG,EG.判断△EFG的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=3,CD=3,点E,F分别在AD,BC上,且AEBC.求EF的取值范围;
(3)如图3,在四边形ABCD中,AB=4,CD=4,∠A+∠D=225°,点E,F分别在AD,BC上,且AEAD,BFBC,求EF的值.
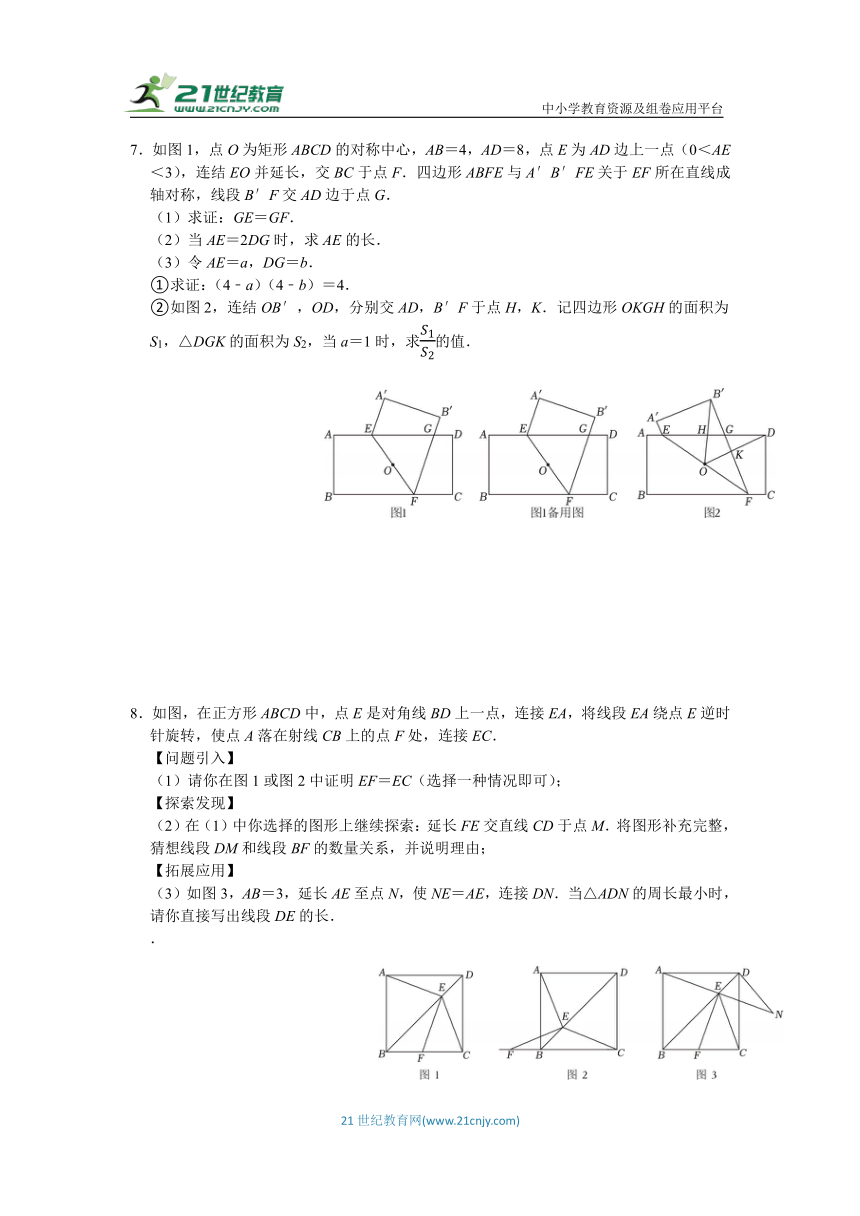
7.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
8.如图,在正方形ABCD中,点E是对角线BD上一点,连接EA,将线段EA绕点E逆时针旋转,使点A落在射线CB上的点F处,连接EC.
【问题引入】
(1)请你在图1或图2中证明EF=EC(选择一种情况即可);
【探索发现】
(2)在(1)中你选择的图形上继续探索:延长FE交直线CD于点M.将图形补充完整,猜想线段DM和线段BF的数量关系,并说明理由;
【拓展应用】
(3)如图3,AB=3,延长AE至点N,使NE=AE,连接DN.当△ADN的周长最小时,请你直接写出线段DE的长.
.
9.如图①,在矩形ABCD中,AB=3,AD=5,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0)
(1)当点P和点B重合时,线段PQ的长为 ;
(2)当点Q和点D重合时,求tan∠PQE;
(3)当点P在边AD上运动时,△PQE的形状始终是等腰直角三角形,如图②,请说明理由;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.
10.如图1,在菱形ABCD中,对角线AC,BD相交于点O,AB=6,∠ABC=60°,点P为线段BO上的动点(不与点B,O重合),连接CP并延长交边AB于点G,交DA的延长线于点H.
(1)当点G恰好为AB的中点时,求证:△AGH≌△BGC;
(2)求线段BD的长;
(3)当△APH为直角三角形时,求的值;
(4)如图2,作线段CG的垂直平分线,交BD于点N,交CG于点M,连接NG,在点P的运动过程中,∠CGN的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.
11.已知:四边形ABCD为矩形,AB=4,AD=3,点F是BC延长线上的一个动点(点F不与点C重合).连接AF交CD于点G.
(1)如图一,当点G为CD的中点时,求证:△ADG≌△FCG;
(2)如图二,过点C作CE⊥AF,垂足为E.连接BE,设BF=x,CE=y.求y关于x的函数关系式;
(3)如图三,在(2)的条件下,过点B作BM⊥BE,交FA的延长线于点M.当CF=1时,求线段BM的长.
12.已知正方形ABCD,E为对角线AC上一点.
【建立模型】
(1)如图1,连接BE,DE.求证:BE=DE;
【模型应用】
(2)如图2,F是DE延长线上一点,FB⊥BE,EF交AB于点G.
①判断△FBG的形状并说明理由;
②若G为AB的中点,且AB=4,求AF的长.
【模型迁移】
(3)如图3,F是DE延长线上一点,FB⊥BE,EF交AB于点G,BE=BF.求证:GE=(1)DE.
13.如图1,在矩形ABCD中,AB=10,AD=8,E是AD边上的一点,连接CE,将矩形ABCD沿CE折叠,顶点D恰好落在AB边上的点F处,延长CE交BA的延长线于点G.
(1)求线段AE的长;
(2)求证四边形DGFC为菱形;
(3)如图2,M,N分别是线段CG,DG上的动点(与端点不重合),且∠DMN=∠DCM,设DN=x,是否存在这样的点N,使△DMN是直角三角形?若存在,请求出x的值;若不存在,请说明理由.
14.已知,四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图1,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图2,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图3,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
15.如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)求证:∠DBG=90°.
(2)若BD=6,DG=2GE.
①求菱形ABCD的面积.
②求tan∠BDE的值.
(3)若BE=AB,当∠DAB的大小发生变化时(0°<∠DAB<180°),在AE上找一点T,使GT为定值,说明理由并求出ET的值.
16.如图,矩形ABCD中,AB=4,AD=3,点E在折线BCD上运动,将AE绕点A顺时针旋转得到AF,旋转角等于∠BAC,连接CF.
(1)当点E在BC上时,作FM⊥AC,垂足为M,求证:AM=AB;
(2)当AE=3时,求CF的长;
(3)连接DF,点E从点B运动到点D的过程中,试探究DF的最小值.
17.如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.
(1)判断由线段AE,EF,BF组成的三角形的形状,并说明理由;
(2)①当a=b时,求∠ECF的度数;
②当a≠b时,①中的结论是否成立?并说明理由.
参考答案
1.【解答】(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴BC=AB=10cm,∠ACB=∠BCD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴yBF EN2(10﹣x)xx2+10x,
∵0<2x≤10,
∴0<x≤5,
∴yx2+10x(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形ABCD是菱形,
∴AD=BC,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
2.【解答】解:(1)由题意得:DQ=10﹣2t,PM=2t,PB=10﹣t,QM=AP=t,
如图,点M在BD上时,
∵QM∥PB,PM∥QD,
∴∠DQM=∠DAB=∠MPQ,∠DMQ=∠MBP,
∴△DQM∽△MPB,则,
即,
解得:t;
(2)如图,
∵AD∥PM,
∴∠AEP=∠EAQ,
∵四边形ABCD是菱形,
则∠QAE=∠EAP,
∴∠AEP=∠EAP,
∴△APE为等腰三角形,则PE=AP=t,
过点D作DH⊥AB于点H,
则S△ABDAB DHAO DB,
即10 DH4,
解得:DH=8,
则sin∠DAH,
设△PEB中PB边上的高为h,
则SPB h(10﹣t)×sin∠DAH×PE(10﹣t)t2+4t(0<t≤5),
∵0,故S有最大值,
当t=5时,S的最大值为10;
(3)存在,理由:
如图,过点B作BR⊥PE于点R,
当点B在∠PEC的平分线上时,则BR=OB=2,
在Rt△PBR中,sin∠EPB=sin∠DAB,
解得:t.
3.【解答】(1)解:结论:点Q在线段PC的垂直平分线上.
理由:连接QC.∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴BD⊥AC,OA=OC,
∴QA=QC,
∵QA=QP,
∴QC=QP,
∴点Q在线段PC的垂直平分线上;
(2)①证明:如图,∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∵BD⊥AC,∴∠ADO=∠CDO,
∴∠ABD=∠CBD=∠ADO.
∵∠BAP=∠ADB,
∴∠BAP=∠ABD=∠CBD.
∴AE=BE,∠APB=90°,∠BAP+∠ABP=90°,∠BAP=∠ABD=∠CBD=30°
在 Rt△BPE 中,∠EPB=90°,∠PBE=30°,
∴EPBE,
∵AE=BE,
∴,
∴AE=2EP;
②如图,连接QC.
∵AB=BC,∠ABC=60°,
∴△ABC 是等边三角形.∠APB=90°,
∴BP=CP,EP=a,
∴AE=2a,AP=3a,
在Rt△APB中,∠APB=90°,
∵,
∴,
∴,
∵AO=CO,∠AOE=∠COQ,OE=OQ,
△AOE≌△COQ(SAS),
∴AE=CQ=2a,∠EAO=∠QCO,
∴AE∥CQ,
∵∠APB=90°,
∴∠QCP=90°,
在Rt△PCQ中,∠QCP=90°,
由勾股定理得 PQ2=PC2+CQ2,
∴PQ2=PC2+CQ2,
∴PQa.
4.【解答】解:(1)在Rt△ABC中,AC,
在Rt△CFG中,CF,
∵AB=GF,BC=CG,
∴AC=CF,
∴△ACF是等腰三角形,
∵AB=GF,∠FGC=∠ABC=90°.BC=CG,
∴△ABC≌△FGC(SAS),
∴∠ACG=∠GFC,
∵∠GCF+∠GFC=90°,
∴∠ACG+∠GCF=90°,
∴∠ACF=90°,
∴△ACF是等腰直角三角形,
故答案为:等腰直角三角形;
(2)探究一:∵CD=GF,∠FMG=∠DMC,∠G=∠CDF=90°,
∴△CDM≌△FGM(AAS),
∴CM=MF,
∵AC=CF,CD⊥AF,
∴AD=DF,
∵AB=CD=2,AD=DF=4,
∴DM=4﹣CM,
在Rt△CDM中,CM2=CD2+DM2,
∴CM2=22+(4﹣CM)2,
解得CM,
∴MF,
∴△CMF的面积2;
探究二:连接DE,取DE的中点P,连接HP,取AD、BC的中点为M、N,连接MN,MH,NH,
∵H是AE的中点,
∴MH∥DE,且MHDE,
∵CD=CE,
∴CP⊥DE,DP=PE,
∵MH∥DP,且MH=DP,
∴四边形MHPD是平行四边形,
∴MD=HP,MD∥HP,
∵AD∥BC,MD=CN,
∴HP∥CN,HP=CN,
∴四边形HNCP是平行四边形,
∴NH∥CP,
∴∠MHN=90°,
∴H点在以MN为直径的圆上,
设MN的中点为T,
∴DT,
∴DH的最大值为1,最小值为1.
方法二:设AC的中点为T,连接HT,
∵HT是△ACE的中位线,
∴HTCE=1,
∴H在以T为圆心,1为半径的圆上,
∵DT,
∴DH的最大值为1,最小值为1.
5.【解答】(1)解:①∵四边形ABCD是正方形,
∴AB=BC=CD=DA.∠ADC=∠BCD=∠DAB=90°,
由题意得CD=CE,∠DCE=α:
∴∠CDE=∠CED(180°﹣α)=90°α.
∴∠ADF=90°﹣∠CDE=90°﹣(90°α)α,
∵AD=AF,
∴∠ADF=∠AFDα,
∴∠FAD=180°﹣∠ADF﹣∠AFD=180°﹣α,
∴∠BAF=∠FAD﹣∠BAD=180°﹣α﹣90°=90°﹣α;
②连接BE.
∵∠DCE=α,
∴∠BCE﹣90°﹣α=∠BAF,
∵CD=CE=AD=AF=BC,
∴△BCE≌△BAF(SAS),
∴BF=BE,∠ABF=∠CBE.
∵∠ABC=90°,
∴∠EBF=90°
∴△EBF是等腰直角三角形,
∴EFBF;
(2)解:过点G作AD的垂线,交直线AD于点H,连接AC,BD相交于点,O,连接OG,
由(1)得△EBF是等腰直角三角形,又点G为斜边EF的中点,
∴BG⊥EF,即∠BGD=90°,
∵四边形ABCD是正方形,
∴OB=OD.
∴OB=OD=OG,
∴点G在以点O为圆心,OB为半径的一段弧上,
当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,
∴GHAB+OGABBD221.
∴△ADG面积的最大值为AD×GH=1.
6.【解答】解:(1)△EFG是直角三角形,
理由:∵点E,F,G分别为AD,BC,AC的中点,
∴GF,GE 分别为△ABC,△ACD 的中位线,
∴FG∥AB,EG∥CD,
∵∠BAC=120°,∠ACD=30°,
∴∠AGF=180°﹣∠BAC=180°﹣120°=60°,∠AGE=∠ACD=30°,
∴∠FGE=∠AGF+∠AGE=60°+30°=90°,
∴△EFG是直角三角形.
(2)如图2,连接AC,在AC上截取ALAC,连接EL,FL,则LCAC,
∵AEAD,BFBC,AB=3,CD=3,
∴FCBC,
∵,∠LCF=∠ACB,
∴△LCF∽△ACB,
∴,
∴LFAB3=2,
∵,∠EAL=∠DAC,
∴△ALE∽△ACD,
∴,
∴LECD3,
∵LF﹣LE<EF≤LF+LE,
∴2EF≤2,
∴EF的取值范围是2EF≤2.
(3)如图3,连接AC,在AC于截取AKAC,连接KE,KF,作EH⊥FK交FK的延长线于点H,
∵AEAD,BFBC,AB=4,CD=4,
∴KCAC,FCBC,
∵,∠KCF=∠ACB,
∴△KCF∽ACB,
∴,∠KFC=∠B,
∴KFAB43,
∵,∠KAE=∠CAD,
∴△AKE∽△ACD,
∴,∠AKE=∠ACD,
∴KECD4,
∵∠BAD+∠D=225°,
∴∠B+∠BCD=360°﹣(∠BAD+∠D)=360°﹣225°=135°,
∵∠AKF=∠KFC+∠ACB=∠B+∠ACB,
∴∠EKF=∠AKF+∠AKE=∠B+∠ACB+∠ACD=∠B+∠BCD=135°,
∴∠HKE=180°﹣∠EKF=180°﹣135°=45°,
∵∠H=90°,
∴∠HEK=∠HKE=45°,
∴HE=HK,
∴KEHK,
∴HE=HK,
∴HF=HK+KF34,
∴EF,
∴EF的值为.
7.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GEF=∠BFE,
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴∠BFE=∠GFE,
∴∠GEF=∠GFE,
∴GE=GF;
(2)解:过G作GH⊥BC于H,如图:
设DG=x,则AE=2x,
∴GE=AD﹣AE﹣DG=8﹣3x=GF,
∵∠GHC=∠C=∠D=90°,
∴四边形GHCD是矩形,
∴GH=CD=AB=4,CH=DG=x,
∵点O为矩形ABCD的对称中心,
∴CF=AE=2x,
∴FH=CF﹣CH=x,
在Rt△GFH中,FH2+GH2=GF2,
∴x2+42=(8﹣3x)2,
解得x=3(此时AE大于AD,舍去)或x=3,
∴AE=2x=6﹣2;
∴AE的长为6﹣2;
(3)①证明:过O作OQ⊥AD于Q,连接OA,OD,OG,如图:
∵点O为矩形ABCD的对称中心,EF过点O,
∴O为EF中点,OA=OD,OQAB=2,
∵GE=GF,
∴OG⊥EF,
∴∠GOQ=90°﹣∠EOQ=∠QEO,
∵∠GQO=90°=∠OQE,
∴△GOQ∽△OEQ,
∴,即GQ EQ=OQ2,
∴GQ EQ=4,
∵OA=OD,OQ⊥AD,
∴AQ=DQAD=4,
∴EQ=AQ﹣AE=4﹣a,GQ=DQ﹣GD=4﹣b,
∴(4﹣a)(4﹣b)=4;
②解:连接B'D,OG,OB,如图:
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴BF=B'F,
∵点O为矩形ABCD的对称中心,
∴BF=DE,
∴B'F=DE,
同理OD=OB=OB',
由(1)知GF=GE,
∴B'F﹣GF=DE﹣GE,即B'G=DG,
∵OG=OG,
∴△DOG≌△B'OG(SSS),
∴∠ODG=∠OB'G,
∵DG=B'G,∠DGK=∠B'GH,
∴△DGK≌△B'GH(ASA),
∴DK=B'H,GK=GH,
∴OD﹣DK=OB'﹣B'H,即OK=OH,
∵OG=OG,
∴△OGK≌△OGH(SSS),
∴S△OGK=S△OGH,
∴S1=2S△OGK,
∴,
∵∠EGF=∠DGB',GE=GF,GD=GB',
∴∠GEF=∠GFE=∠GDB'=∠GB'D,
∴EF∥B'D,
∴△OKF∽△DKB',△EGF∽△DGB',
∴,
∵,
∴,
∵△EGF∽△DGB',
∴,
当a=1时,由①知(4﹣1)×(4﹣b)=4,
∴b,
∴AE=1,DG,
∴GE=AD﹣AE﹣DG,
∴,
∴的值为.
8.【解答】(1)证明:选择图1,
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC,
由旋转得:EA=EF,
∴EF=EC.
选择图2,
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC,
由旋转得:EA=EF,
∴EF=EC.
(2)解:猜想DM=BF.理由如下:
选择图1,过点F作FH⊥BC交BD于点H,
则∠HFB=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠HFB=∠BCD,
∴FH∥CD,
∴∠HFE=∠M,
∵EF=EC,
∴∠EFC=∠ECF,
∵∠FCD=90°,
∴∠EFC+∠M=90°,∠ECD+∠ECF=90°,
∴∠M=∠ECM,
∴EC=EM,
∴EF=EM,
∵∠HEF=∠DEM,
∴△HEF≌△DEM(ASA),
∴DM=FH,
∵∠HBF=45°,∠BFH=90°,
∴∠BHF=45°,
∴BF=FH,
∴DM=BF.
若选择图2,过点F作FH⊥BC交DB的延长线于点H,
则∠HFB=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠HFB=∠BCD,
∴FH∥CD,
∴∠H=∠EDM,
∵EF=EC,
∴∠EFC=∠ECF,
∵∠EFC+∠FMC=90°,∠ECF+∠ECM=90°,
∴∠FMC=∠ECM,
∴EC=EM,
∴EF=EM,
∵∠HEF=∠DEM,
∴△HEF≌△DEM(AAS),
∴FH=DM,
∵∠DBC=45°,
∴∠FBH=45°,
∴∠H=45°,
∴BF=FH,
∴DM=BF.
(3)解:如图3,取AD的中点G,连接EG,
∵NE=AE,
∴点E是AN的中点,
∴EGDN,
∵△ADN的周长=AD+DN+AN=3+2(AE+EG),
∴当△ADN的周长最小时,AE+EG最小,此时,C、E、G三点共线,如图4,
∵四边形ABCD是正方形,
∴AB=AD=BC=3,AD∥BC,∠BAD=90°,
在Rt△ABD中,BD=3,
∵点G是AD的中点,
∴DGAD,,
∵AD∥BC,
∴△DEG∽△BEC,
∴,
∴BE=2DE,
∵BE+DE=BD=3,
∴2DE+DE=3,即3DE=3,
∴DE.
9.【解答】解:如图所示,连接BQ,
∵四边形ABCD是矩形,
∴∠BAQ=∠ABE=90°,
∵∠PEQ=90°,
∴四边形ABEQ是矩形,
当点P和点B重合时,
∴QE=AB=3,BE=2,
在Rt△QBE中,,
故答案为:.
(2)如图所示,
∵∠PEQ=90°,∠PBE=∠ECD=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴△PBE∽△ECD,
∴,
∵BE=2,CD=AB=3,
∴.
(3)如图所示,过点P作PH⊥BC于点H,
∵∠PEQ=90°,∠PHE=∠ECQ=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵四边形ABCD是矩形,
∴四边形ABHP是矩形,
∴PH=AB=3,
又∵EC=BC﹣BE=5﹣2=3,
∴PH=EC,
∴△PHE≌ECQ(ASA),
∴PE=QE,
∴△PQE 是等腰直角三角形;
(4)①如图所示,当点P在BE上时,
∵QE=QF=3,AQ=BE=2,
在Rt△AQF中,,
则 ,
∵PE=t,
∴BP=2﹣t,PF=PE=t,
在Rt△PBF中,PF2=PB2+FB2,
∴,
解得:,
当 时,点F在矩形内部,
∴0<t符合题意.
②当P点在AB上时,当F,A重合时符合题意,此时如图,
则PB=t﹣BE=t﹣2,PE=AP=AB﹣PB=3﹣(t﹣2)=5﹣t,
在Rt△PBE中,PE2=PB2+BE2,
∴(5﹣t)2=(t﹣2)2+22,
解得t.
③当点P在AD上,当F,D重合时,此时点Q与点C重合,则PFQE是正方形,此时t=2+3+2=7.
综上所述,0<t或t或t=7.
10.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠HAB=∠ABC,
∵点G是AB的中点,
∴AG=BG,
又∵∠AGH=∠BGC,
∴△AGH≌△BGC(AAS);
(2)解:∵四边形ABCD是菱形,
∴AO=CO,BO=DO,AC⊥BD,∠ABD∠ABC=30°,
∴AOAB=3,BOAO=3,
∴BD=6;
(3)解:当∠PAD=90°时,
∵四边形ABCD是菱形,
∴∠ABC=∠ADC=60°,∠ADB∠ADC=30°,
∴ADAP=6,PD=2AP,
∴AP=2,DP=4,
∴BP=2,
∵AD∥BC,
∴△BPC∽△DPH,
∴,
∴2;
当∠APH=90°时,
∴∠DPA=∠DPC=45°,
∴AO=PO=3,
∴BP=33,DP=33,
∵AD∥BC,
∴△BPC∽△DPH,
∴,
∴2;
综上所述:2或2;
(4)解:∠CGN的度数是定值,
如图,取BC的中点H,连接OH,HM,NC,
∵MN是CG的垂直平分线,
∴GN=CN,GM=CM,
∴∠NGC=∠GCN,
又∵点H是BC的中点,
∴MH∥AB,
∵点H是BC的中点,AO=CO,
∴OH∥AB,
∴点M,点H,点O三点共线,
∵点H是BC的中点,AC⊥BD,
∴HO=HB=CH,
∴∠CBO=∠BOH=30°,
∵∠COB=∠NMC=90°,
∴点O,点C,点M,点N四点共圆,
∴∠BOH=∠NCM=30°,
∴∠CGN=∠NCM=30°.
11.【解答】(1)证明:∵四边形ABCD为矩形,
.∴AD∥BF,
∴∠D=∠DCF,
∵G为CD中点,
∴DG=CG,
∵∠AGD=∠FGC,
∴△ADG≌△FCG(ASA);
(2)解:∵四边形ABCD为矩形,
∴∠ABC=90°,
∵CE⊥AF,
∴∠CEF=90°=∠ABC,
∵∠F=∠F,
∴△CEF∽△ABF,
∴,
∵AB=4,BF=x,
在Rt△ABF中,AF,
∵CE=y,
∴,
∴y(或者y);
(3)解:过点E作EN⊥BF于点N,
∵四边形ABCD为矩形,AD=3,
∴AD=BC=3,
∵AB=4,CF=1,
∴AB=BF,
∴△ABF为等腰直角三角形,
∴∠CFE=∠BAF=45°,
∵CE⊥AF,
∴△CEF为等腰直角三角形,
∴∠ECF=45°,
∵EN⊥CF,
∴EN平分CF,
∴CN=NF=NE,
在Rt△BNE中,根据勾股定理得:
BE2=BN2+EN2,
∴BE,
∵∠ECF=∠BAF=45°,
∴∠BAM=∠BCE=135°,
∵BM⊥BE,
∴∠MBA+∠ABE=90°,
∠ABE+∠EBC=90°,
∴∠MBA=∠EBC,
∴△BAM∽△BCE,
∴,
∴,
∴BM.
12.【解答】(1)证明:∵AC是正方形ABCD的对角线,
∴AB=AD,∠BAE=∠DAE=45°,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)解:①△FBG为等腰三角形,理由:
∵四边形ABCD是正方形,
∴∠GAD=90°,
∴∠AGD+∠ADG=90°,
由(1)知,△ABE≌△ADE,
∴∠ADG=∠EBG,
∴∠AGD+∠EBG=90°,
∵FB⊥BE,
∴∠FBG+∠EBG=90°,
∴∠AGD=∠FBG,
∵∠AGD=∠FGB,
∴∠FBG=∠FGB,
∴FG=FB,
∴△FBG是等腰三角形;
②如图,过点F作FH⊥AB于H,
∵四边形ABCD为正方形,点G为AB的中点,AB=4,
∴AG=BG=2,AD=4,
由①知,FG=FB,
∴GH=BH=1,
∴AH=AG+GH=3,
在Rt△FHG与Rt△DAG中,∵∠FGH=∠DGA,
∴tan∠FGH=tan∠DGA,
∴2,
∴FH=2GH=2,
在Rt△AHF中,AF;
(3)∵FB⊥BE,
∴∠FBE=90°,
在Rt△EBF中,BE=BF,
∴EFBE,
由(1)知,BE=DE,
由(2)知,FG=BF,
∴GE=EF﹣FGBE﹣BFDE﹣DE=(1)DE.
13.【解答】(1)解:∵四边形ABCD是矩形,
∴∠DAB=∠B=∠ADC=90°,CD=AB=10,BC=AD=8,
在Rt△BCF中,CF=CD=10,BC=8,
∴BF=6,
∴AF=AB﹣BF=4,
设AE=x,则EF=DE=8﹣x,
在Rt△AEF中,由勾股定理得,
EF2﹣AE2=AF2,
∴(8﹣x)2﹣x2=42,
∴x=3,
∴AE=3;
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴△AGE∽△DCE,
∴,
由(1)得:AE=3,
∴DE=8﹣3=5,
∴,
∴AG=6,
∴FG=AF+AG=4+6=10,
∴FG=CD,
∴四边形DGFC是平行四边形,
∵CD=CF,
∴ DGFC是菱形;
(3)解:∵四边形FGDC是菱形,
∴∠DGC=∠DCG=∠FGC,DG=CD=10,
在Rt△BCG中,BC=8,BG=BF+FG=6+10=16,
∴tan∠FGC,CG8,
∴sin∠FCG,
如图1,
当∠MDN=90°时,
在Rt△GDM中,
DM=DG tan∠DGM=10 tan∠FGC=105,
在Rt△DMN中,
DN=DM tan∠DMN,
∵∠DMN=∠DCM,∠DCM=∠FGC,
∴DN=DM tan∠FGC=5,
如图2,
当∠MND=90°时,∠DMN+∠GDM=90°,
∵∠DMN=∠DCM=∠DGM,
∴∠DGM+∠GDM=90°,
∴∠DMG=90°,
∴DM=DG sin∠DGM=102,
在Rt△DMN中,
DN=DM sin∠DMN=DM sin∠FGC=22,
综上所述:DN或2.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°.
∵DE=DF,∠EDF=90°.
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS);
(2)①证明:如图2中,设AG与CD相交于点P.
∵∠ADP=90°,
∴∠DAP+∠DPA=90°.
∵△ADE≌△CDF,
∴∠DAE=∠DCF.
∵∠DPA=∠GPC,
∴∠DAE+∠DPA=∠GPC+∠GCP=90°.
∴∠PGN=90°,
∵BM⊥AG,BN⊥GN,
∴四边形BMGN是矩形,
∴∠MBN=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠MBN=90°.
∴∠ABM=∠CBN.
又∵∠AMB=∠BNC=90°,
∴△AMB≌△CNB.
∴MB=NB.
∴矩形BMGN是正方形;
②解:作DH⊥AG交AG于点H,作BM⊥AG于点M,
此时△AMB≌△AHD.
∴BM=AH.
∵AH2=AD2﹣DH2,AD=4,
∴DH最大时,AH最小,DH最大值=DE=2.
∴BM最小值=AH最小值.
由(2)①可知,△BGM是等腰直角三角形,
∴BG最小值.
15.【解答】(1)证明:如图1,∵四边形ABCD是菱形,
∴CB=AB,CD=AD,
∵BD=BD,
∴△ABD≌△CBD,
∴∠CBD=∠ABD∠ABC,
∵∠CBG=∠EBG∠EBC,
∴∠DBG=∠CBD+∠CBG(∠ABC+∠EBC)180°=90°.
(2)解:①如图2,连结AC交BD于点K,交DE于点L,
∵AC⊥BD,
∴∠AKB=90°,
∵AB=5,BD=6,
∴BK=DKBD=3,
∴AK4,
∴CK=AK=4,
∴AC=8,
∴S菱形ABCDAC BD8×6=24.
②∵∠DKL=∠DBG=90°,
∴AC∥BG,
∴1,
∴DL=GLDG,
∵DG=2GE,
∴GEDG,
∴DL=GL=GE,
∵CD∥AB,
∴,
∴CLAC8,
∴KL=4,
∴tan∠BDE.
(3)解:如图3,过点G作GT∥BC,交AE于点T,则GT为定值,
理由:连结AC交BD于点K,交DE于点L,
∵∠DKL=∠DBG=90°,
∴当∠DAB的大小发生变化时,始终都有BG∥AC,
∴△BGE∽△ALE,
∵BE=AB,
∴1,
∴EG=LG,
∵KL∥BG,
∴1,
∴DL=LG=EGED,
∵AD∥BC,
∴GT∥AD,
∴△ETG∽△EAD,
∴,
∵BE=AB=DA=5,
∴GTDA5,
∴GT为定值;
∵EA=BE+AB=10,
∴ETEA10.
16.【解答】(1)证明:如图1中,作FM⊥AC,垂足为M,
∵四边形ABCD是矩形,
∴∠B=90°,
∵FM⊥AC,
∴∠B=∠AMF=90°,
∵∠BAC=∠EAF,
∴∠BAE=∠MAF,
在△ABE和△AMF中,
,
∴△ABE≌△AMF(AAS),
∴AB=AM;
(2)解:当点E在BC上,在Rt△ABE中,AB=4,AE=3,
∴BE,
∵△ABE≌△AMF,
∴AB=AM=4,FM=BE,
在Rt△ABC中,AB=4,BC=3,
∴AC5,
∴CM=AC﹣AM=5﹣4=1,
∵∠CMF=90°,
∴CF.
当点E在CD上时,作FH⊥AC于点H,可证DE=AD=AH=FH=3,CH=2,
可得CF.
综上所述,CF的值为或;
(3)解:当点E在BC上时,如图2中,过点D作DH⊥FM于点H.
∵△ABE≌△AMF,
∴AM=AB=4,
∵∠AMF=90°,
∴点F在射线FM上运动,当点F与K重合时,DF的值最小,
∵∠CMJ=∠ADC=90°,∠MCJ=∠ACD,
∴△CMJ∽△CDA,
∴,
∴,
∴MJ,CJ,
∴DJ=CD﹣CJ=4,
∵∠CMJ=∠DHJ=90°,∠CJM=∠DJH,
∴△CMJ∽△DHJ,
∴,
∴,
∴DH,
∴DF的最小值为.
当点E在线段CD上时,如图3中,将线段AD绕点A顺时针旋转,旋转角为∠BAC,得到线段AR,连接FR,过点D作DQ⊥AR于点Q,DK⊥FR于点K.
∵∠EAF=∠BAC,∠DAR=∠BAC,
∴∠DAE=∠RAF,
∵AE=AF,AD=AR,
∴△ADE≌△ARF(SAS),
∴∠ADE=∠ARF=90°,
∴点F在直线RF上运动,当点D与K重合时,DF的值最小,
∵DQ⊥AR,DK⊥RF,
∴∠R=∠DQR=∠DKR=90°,
∴四边形DKRQ是矩形,
∴DK=QR,
∴AQ=AD cos∠BAC=3,
∵AR=AD=3,
∴DK=QR=AR﹣AQ,
∴DF的最小值为,
∵,
∴DF的最小值为.
解法二:当点E在BC上时,如图,将线段AD绕点A逆时针旋转,旋转角的度数=∠BAC,得到AT,连接DT,ET,DF.
证明△DAF≌△TAE,推出DF=TE,
当TE⊥BC时,DF的值最小,可得DF的最小值为.
当点E在CD上时,同法可得DF的最小值为.
17.【解答】解:(1)线段AE,EF,BF组成的是直角三角形,理由如下:
∵AM=AC﹣CM=4﹣a,BN=4﹣b,
∴AE,BF,
∴AE2+BF2=2(4﹣a)2+2(4﹣b)2=2(a2+b2﹣8a﹣8b+32),
∵AB4,
∴EF=AB﹣AE﹣BF[4﹣(4﹣a)﹣(4﹣b)](a+b﹣4),
∵ab=8,
EF2=2(a+b﹣4)2=2(a2+b2﹣8a﹣8b+16+2ab)=2(a2+b2﹣8a﹣8b+32),
∴AE2+BF2=EF2,
∴线段AE,EF,BF组成的是直角三角形;
(2)①如图1,
连接PC交EF于G,
∵a=b,
∴ME=AM=BN=NF,
∵四边形CNPM是矩形,
∴矩形CNPM是正方形,
∴PC平分∠ACB,
∴CG⊥AB,
∴∠PGE=90°,
∵CM=CN=PM=PN,
∴PE=PF,
∵△AEM,△BNF,△PEF是等腰直角三角形,
EF2=AE2+BF2,EF2=PE2+PF2,
∴PE=AE=PF=BF,
∴ME=EG=FG=FN,
∴∠MCE=∠GCE,∠NCF=∠GCF,
∵∠ACB=90°,
∴∠ECG+∠FCG,
∴∠ECF=45°;
②如图2,
仍然成立,理由如下:
将△BCF逆时针旋转90°至△ACD,连接DE,
∴∠DAC=∠B=45°,AD=BF,
∴∠DAE=∠DAC+∠CAB=90°,
∴DE2=AD2+AE2=BF2+AE2
∵EF2=BF2+AE2,
∴DE=EF,
∵CD=CF,CE=CE,
∴△DCE≌△FCE(SSS),
∴∠ECF=∠DCE.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/3/15 10:19:43;用户:永州综合中专;邮箱:yzzh66@;学号:48626927
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练四边形压轴题训练
1.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=10cm,BD=4cm.动点P从点A出发,沿AB方向匀速运动,速度为1cm/s;同时,动点Q从点A出发,沿AD方向匀速运动,速度为2cm/s.以AP,AQ为邻边的平行四边形APMQ的边PM与AC交于点E.设运动时间为t(s)(0<t≤5),解答下列问题:
(1)当点M在BD上时,求t的值;
(2)连接BE.设△PEB的面积为S(cm2),求S与t的函数关系式和S的最大值;
(3)是否存在某一时刻t,使点B在∠PEC的平分线上?若存在,求出t的值;若不存在,请说明理由.
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
4.在数学综合与实践活动课上,小红以“矩形的旋转”为主题开展探究活动.
(1)操作判断
小红将两个完全相同的矩形纸片ABCD和CEFG拼成“L”形图案,如图①.试判断:△ACF的形状为 .
(2)深入探究
小红在保持矩形ABCD不动的条件下,将矩形CEFG绕点C旋转,若AB=2,AD=4.
探究一:当点F恰好落在AD的延长线上时,设CG与DF相交于点M,如图②.求△CMF的面积.
探究二:连接AE,取AE的中点H,连接DH,如图③.求线段DH长度的最大值和最小值.
5.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
6.(1)如图1,AC为四边形ABCD的对角线,∠BAC=120°,∠ACD=30°,E,F,G分别为AD,BC,AC的中点,连接EF,FG,EG.判断△EFG的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=3,CD=3,点E,F分别在AD,BC上,且AEBC.求EF的取值范围;
(3)如图3,在四边形ABCD中,AB=4,CD=4,∠A+∠D=225°,点E,F分别在AD,BC上,且AEAD,BFBC,求EF的值.
7.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
8.如图,在正方形ABCD中,点E是对角线BD上一点,连接EA,将线段EA绕点E逆时针旋转,使点A落在射线CB上的点F处,连接EC.
【问题引入】
(1)请你在图1或图2中证明EF=EC(选择一种情况即可);
【探索发现】
(2)在(1)中你选择的图形上继续探索:延长FE交直线CD于点M.将图形补充完整,猜想线段DM和线段BF的数量关系,并说明理由;
【拓展应用】
(3)如图3,AB=3,延长AE至点N,使NE=AE,连接DN.当△ADN的周长最小时,请你直接写出线段DE的长.
.
9.如图①,在矩形ABCD中,AB=3,AD=5,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0)
(1)当点P和点B重合时,线段PQ的长为 ;
(2)当点Q和点D重合时,求tan∠PQE;
(3)当点P在边AD上运动时,△PQE的形状始终是等腰直角三角形,如图②,请说明理由;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.
10.如图1,在菱形ABCD中,对角线AC,BD相交于点O,AB=6,∠ABC=60°,点P为线段BO上的动点(不与点B,O重合),连接CP并延长交边AB于点G,交DA的延长线于点H.
(1)当点G恰好为AB的中点时,求证:△AGH≌△BGC;
(2)求线段BD的长;
(3)当△APH为直角三角形时,求的值;
(4)如图2,作线段CG的垂直平分线,交BD于点N,交CG于点M,连接NG,在点P的运动过程中,∠CGN的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.
11.已知:四边形ABCD为矩形,AB=4,AD=3,点F是BC延长线上的一个动点(点F不与点C重合).连接AF交CD于点G.
(1)如图一,当点G为CD的中点时,求证:△ADG≌△FCG;
(2)如图二,过点C作CE⊥AF,垂足为E.连接BE,设BF=x,CE=y.求y关于x的函数关系式;
(3)如图三,在(2)的条件下,过点B作BM⊥BE,交FA的延长线于点M.当CF=1时,求线段BM的长.
12.已知正方形ABCD,E为对角线AC上一点.
【建立模型】
(1)如图1,连接BE,DE.求证:BE=DE;
【模型应用】
(2)如图2,F是DE延长线上一点,FB⊥BE,EF交AB于点G.
①判断△FBG的形状并说明理由;
②若G为AB的中点,且AB=4,求AF的长.
【模型迁移】
(3)如图3,F是DE延长线上一点,FB⊥BE,EF交AB于点G,BE=BF.求证:GE=(1)DE.
13.如图1,在矩形ABCD中,AB=10,AD=8,E是AD边上的一点,连接CE,将矩形ABCD沿CE折叠,顶点D恰好落在AB边上的点F处,延长CE交BA的延长线于点G.
(1)求线段AE的长;
(2)求证四边形DGFC为菱形;
(3)如图2,M,N分别是线段CG,DG上的动点(与端点不重合),且∠DMN=∠DCM,设DN=x,是否存在这样的点N,使△DMN是直角三角形?若存在,请求出x的值;若不存在,请说明理由.
14.已知,四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图1,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图2,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图3,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
15.如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)求证:∠DBG=90°.
(2)若BD=6,DG=2GE.
①求菱形ABCD的面积.
②求tan∠BDE的值.
(3)若BE=AB,当∠DAB的大小发生变化时(0°<∠DAB<180°),在AE上找一点T,使GT为定值,说明理由并求出ET的值.
16.如图,矩形ABCD中,AB=4,AD=3,点E在折线BCD上运动,将AE绕点A顺时针旋转得到AF,旋转角等于∠BAC,连接CF.
(1)当点E在BC上时,作FM⊥AC,垂足为M,求证:AM=AB;
(2)当AE=3时,求CF的长;
(3)连接DF,点E从点B运动到点D的过程中,试探究DF的最小值.
17.如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.
(1)判断由线段AE,EF,BF组成的三角形的形状,并说明理由;
(2)①当a=b时,求∠ECF的度数;
②当a≠b时,①中的结论是否成立?并说明理由.
参考答案
1.【解答】(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴BC=AB=10cm,∠ACB=∠BCD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴yBF EN2(10﹣x)xx2+10x,
∵0<2x≤10,
∴0<x≤5,
∴yx2+10x(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形ABCD是菱形,
∴AD=BC,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
2.【解答】解:(1)由题意得:DQ=10﹣2t,PM=2t,PB=10﹣t,QM=AP=t,
如图,点M在BD上时,
∵QM∥PB,PM∥QD,
∴∠DQM=∠DAB=∠MPQ,∠DMQ=∠MBP,
∴△DQM∽△MPB,则,
即,
解得:t;
(2)如图,
∵AD∥PM,
∴∠AEP=∠EAQ,
∵四边形ABCD是菱形,
则∠QAE=∠EAP,
∴∠AEP=∠EAP,
∴△APE为等腰三角形,则PE=AP=t,
过点D作DH⊥AB于点H,
则S△ABDAB DHAO DB,
即10 DH4,
解得:DH=8,
则sin∠DAH,
设△PEB中PB边上的高为h,
则SPB h(10﹣t)×sin∠DAH×PE(10﹣t)t2+4t(0<t≤5),
∵0,故S有最大值,
当t=5时,S的最大值为10;
(3)存在,理由:
如图,过点B作BR⊥PE于点R,
当点B在∠PEC的平分线上时,则BR=OB=2,
在Rt△PBR中,sin∠EPB=sin∠DAB,
解得:t.
3.【解答】(1)解:结论:点Q在线段PC的垂直平分线上.
理由:连接QC.∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴BD⊥AC,OA=OC,
∴QA=QC,
∵QA=QP,
∴QC=QP,
∴点Q在线段PC的垂直平分线上;
(2)①证明:如图,∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∵BD⊥AC,∴∠ADO=∠CDO,
∴∠ABD=∠CBD=∠ADO.
∵∠BAP=∠ADB,
∴∠BAP=∠ABD=∠CBD.
∴AE=BE,∠APB=90°,∠BAP+∠ABP=90°,∠BAP=∠ABD=∠CBD=30°
在 Rt△BPE 中,∠EPB=90°,∠PBE=30°,
∴EPBE,
∵AE=BE,
∴,
∴AE=2EP;
②如图,连接QC.
∵AB=BC,∠ABC=60°,
∴△ABC 是等边三角形.∠APB=90°,
∴BP=CP,EP=a,
∴AE=2a,AP=3a,
在Rt△APB中,∠APB=90°,
∵,
∴,
∴,
∵AO=CO,∠AOE=∠COQ,OE=OQ,
△AOE≌△COQ(SAS),
∴AE=CQ=2a,∠EAO=∠QCO,
∴AE∥CQ,
∵∠APB=90°,
∴∠QCP=90°,
在Rt△PCQ中,∠QCP=90°,
由勾股定理得 PQ2=PC2+CQ2,
∴PQ2=PC2+CQ2,
∴PQa.
4.【解答】解:(1)在Rt△ABC中,AC,
在Rt△CFG中,CF,
∵AB=GF,BC=CG,
∴AC=CF,
∴△ACF是等腰三角形,
∵AB=GF,∠FGC=∠ABC=90°.BC=CG,
∴△ABC≌△FGC(SAS),
∴∠ACG=∠GFC,
∵∠GCF+∠GFC=90°,
∴∠ACG+∠GCF=90°,
∴∠ACF=90°,
∴△ACF是等腰直角三角形,
故答案为:等腰直角三角形;
(2)探究一:∵CD=GF,∠FMG=∠DMC,∠G=∠CDF=90°,
∴△CDM≌△FGM(AAS),
∴CM=MF,
∵AC=CF,CD⊥AF,
∴AD=DF,
∵AB=CD=2,AD=DF=4,
∴DM=4﹣CM,
在Rt△CDM中,CM2=CD2+DM2,
∴CM2=22+(4﹣CM)2,
解得CM,
∴MF,
∴△CMF的面积2;
探究二:连接DE,取DE的中点P,连接HP,取AD、BC的中点为M、N,连接MN,MH,NH,
∵H是AE的中点,
∴MH∥DE,且MHDE,
∵CD=CE,
∴CP⊥DE,DP=PE,
∵MH∥DP,且MH=DP,
∴四边形MHPD是平行四边形,
∴MD=HP,MD∥HP,
∵AD∥BC,MD=CN,
∴HP∥CN,HP=CN,
∴四边形HNCP是平行四边形,
∴NH∥CP,
∴∠MHN=90°,
∴H点在以MN为直径的圆上,
设MN的中点为T,
∴DT,
∴DH的最大值为1,最小值为1.
方法二:设AC的中点为T,连接HT,
∵HT是△ACE的中位线,
∴HTCE=1,
∴H在以T为圆心,1为半径的圆上,
∵DT,
∴DH的最大值为1,最小值为1.
5.【解答】(1)解:①∵四边形ABCD是正方形,
∴AB=BC=CD=DA.∠ADC=∠BCD=∠DAB=90°,
由题意得CD=CE,∠DCE=α:
∴∠CDE=∠CED(180°﹣α)=90°α.
∴∠ADF=90°﹣∠CDE=90°﹣(90°α)α,
∵AD=AF,
∴∠ADF=∠AFDα,
∴∠FAD=180°﹣∠ADF﹣∠AFD=180°﹣α,
∴∠BAF=∠FAD﹣∠BAD=180°﹣α﹣90°=90°﹣α;
②连接BE.
∵∠DCE=α,
∴∠BCE﹣90°﹣α=∠BAF,
∵CD=CE=AD=AF=BC,
∴△BCE≌△BAF(SAS),
∴BF=BE,∠ABF=∠CBE.
∵∠ABC=90°,
∴∠EBF=90°
∴△EBF是等腰直角三角形,
∴EFBF;
(2)解:过点G作AD的垂线,交直线AD于点H,连接AC,BD相交于点,O,连接OG,
由(1)得△EBF是等腰直角三角形,又点G为斜边EF的中点,
∴BG⊥EF,即∠BGD=90°,
∵四边形ABCD是正方形,
∴OB=OD.
∴OB=OD=OG,
∴点G在以点O为圆心,OB为半径的一段弧上,
当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,
∴GHAB+OGABBD221.
∴△ADG面积的最大值为AD×GH=1.
6.【解答】解:(1)△EFG是直角三角形,
理由:∵点E,F,G分别为AD,BC,AC的中点,
∴GF,GE 分别为△ABC,△ACD 的中位线,
∴FG∥AB,EG∥CD,
∵∠BAC=120°,∠ACD=30°,
∴∠AGF=180°﹣∠BAC=180°﹣120°=60°,∠AGE=∠ACD=30°,
∴∠FGE=∠AGF+∠AGE=60°+30°=90°,
∴△EFG是直角三角形.
(2)如图2,连接AC,在AC上截取ALAC,连接EL,FL,则LCAC,
∵AEAD,BFBC,AB=3,CD=3,
∴FCBC,
∵,∠LCF=∠ACB,
∴△LCF∽△ACB,
∴,
∴LFAB3=2,
∵,∠EAL=∠DAC,
∴△ALE∽△ACD,
∴,
∴LECD3,
∵LF﹣LE<EF≤LF+LE,
∴2EF≤2,
∴EF的取值范围是2EF≤2.
(3)如图3,连接AC,在AC于截取AKAC,连接KE,KF,作EH⊥FK交FK的延长线于点H,
∵AEAD,BFBC,AB=4,CD=4,
∴KCAC,FCBC,
∵,∠KCF=∠ACB,
∴△KCF∽ACB,
∴,∠KFC=∠B,
∴KFAB43,
∵,∠KAE=∠CAD,
∴△AKE∽△ACD,
∴,∠AKE=∠ACD,
∴KECD4,
∵∠BAD+∠D=225°,
∴∠B+∠BCD=360°﹣(∠BAD+∠D)=360°﹣225°=135°,
∵∠AKF=∠KFC+∠ACB=∠B+∠ACB,
∴∠EKF=∠AKF+∠AKE=∠B+∠ACB+∠ACD=∠B+∠BCD=135°,
∴∠HKE=180°﹣∠EKF=180°﹣135°=45°,
∵∠H=90°,
∴∠HEK=∠HKE=45°,
∴HE=HK,
∴KEHK,
∴HE=HK,
∴HF=HK+KF34,
∴EF,
∴EF的值为.
7.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GEF=∠BFE,
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴∠BFE=∠GFE,
∴∠GEF=∠GFE,
∴GE=GF;
(2)解:过G作GH⊥BC于H,如图:
设DG=x,则AE=2x,
∴GE=AD﹣AE﹣DG=8﹣3x=GF,
∵∠GHC=∠C=∠D=90°,
∴四边形GHCD是矩形,
∴GH=CD=AB=4,CH=DG=x,
∵点O为矩形ABCD的对称中心,
∴CF=AE=2x,
∴FH=CF﹣CH=x,
在Rt△GFH中,FH2+GH2=GF2,
∴x2+42=(8﹣3x)2,
解得x=3(此时AE大于AD,舍去)或x=3,
∴AE=2x=6﹣2;
∴AE的长为6﹣2;
(3)①证明:过O作OQ⊥AD于Q,连接OA,OD,OG,如图:
∵点O为矩形ABCD的对称中心,EF过点O,
∴O为EF中点,OA=OD,OQAB=2,
∵GE=GF,
∴OG⊥EF,
∴∠GOQ=90°﹣∠EOQ=∠QEO,
∵∠GQO=90°=∠OQE,
∴△GOQ∽△OEQ,
∴,即GQ EQ=OQ2,
∴GQ EQ=4,
∵OA=OD,OQ⊥AD,
∴AQ=DQAD=4,
∴EQ=AQ﹣AE=4﹣a,GQ=DQ﹣GD=4﹣b,
∴(4﹣a)(4﹣b)=4;
②解:连接B'D,OG,OB,如图:
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴BF=B'F,
∵点O为矩形ABCD的对称中心,
∴BF=DE,
∴B'F=DE,
同理OD=OB=OB',
由(1)知GF=GE,
∴B'F﹣GF=DE﹣GE,即B'G=DG,
∵OG=OG,
∴△DOG≌△B'OG(SSS),
∴∠ODG=∠OB'G,
∵DG=B'G,∠DGK=∠B'GH,
∴△DGK≌△B'GH(ASA),
∴DK=B'H,GK=GH,
∴OD﹣DK=OB'﹣B'H,即OK=OH,
∵OG=OG,
∴△OGK≌△OGH(SSS),
∴S△OGK=S△OGH,
∴S1=2S△OGK,
∴,
∵∠EGF=∠DGB',GE=GF,GD=GB',
∴∠GEF=∠GFE=∠GDB'=∠GB'D,
∴EF∥B'D,
∴△OKF∽△DKB',△EGF∽△DGB',
∴,
∵,
∴,
∵△EGF∽△DGB',
∴,
当a=1时,由①知(4﹣1)×(4﹣b)=4,
∴b,
∴AE=1,DG,
∴GE=AD﹣AE﹣DG,
∴,
∴的值为.
8.【解答】(1)证明:选择图1,
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC,
由旋转得:EA=EF,
∴EF=EC.
选择图2,
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC,
由旋转得:EA=EF,
∴EF=EC.
(2)解:猜想DM=BF.理由如下:
选择图1,过点F作FH⊥BC交BD于点H,
则∠HFB=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠HFB=∠BCD,
∴FH∥CD,
∴∠HFE=∠M,
∵EF=EC,
∴∠EFC=∠ECF,
∵∠FCD=90°,
∴∠EFC+∠M=90°,∠ECD+∠ECF=90°,
∴∠M=∠ECM,
∴EC=EM,
∴EF=EM,
∵∠HEF=∠DEM,
∴△HEF≌△DEM(ASA),
∴DM=FH,
∵∠HBF=45°,∠BFH=90°,
∴∠BHF=45°,
∴BF=FH,
∴DM=BF.
若选择图2,过点F作FH⊥BC交DB的延长线于点H,
则∠HFB=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠HFB=∠BCD,
∴FH∥CD,
∴∠H=∠EDM,
∵EF=EC,
∴∠EFC=∠ECF,
∵∠EFC+∠FMC=90°,∠ECF+∠ECM=90°,
∴∠FMC=∠ECM,
∴EC=EM,
∴EF=EM,
∵∠HEF=∠DEM,
∴△HEF≌△DEM(AAS),
∴FH=DM,
∵∠DBC=45°,
∴∠FBH=45°,
∴∠H=45°,
∴BF=FH,
∴DM=BF.
(3)解:如图3,取AD的中点G,连接EG,
∵NE=AE,
∴点E是AN的中点,
∴EGDN,
∵△ADN的周长=AD+DN+AN=3+2(AE+EG),
∴当△ADN的周长最小时,AE+EG最小,此时,C、E、G三点共线,如图4,
∵四边形ABCD是正方形,
∴AB=AD=BC=3,AD∥BC,∠BAD=90°,
在Rt△ABD中,BD=3,
∵点G是AD的中点,
∴DGAD,,
∵AD∥BC,
∴△DEG∽△BEC,
∴,
∴BE=2DE,
∵BE+DE=BD=3,
∴2DE+DE=3,即3DE=3,
∴DE.
9.【解答】解:如图所示,连接BQ,
∵四边形ABCD是矩形,
∴∠BAQ=∠ABE=90°,
∵∠PEQ=90°,
∴四边形ABEQ是矩形,
当点P和点B重合时,
∴QE=AB=3,BE=2,
在Rt△QBE中,,
故答案为:.
(2)如图所示,
∵∠PEQ=90°,∠PBE=∠ECD=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴△PBE∽△ECD,
∴,
∵BE=2,CD=AB=3,
∴.
(3)如图所示,过点P作PH⊥BC于点H,
∵∠PEQ=90°,∠PHE=∠ECQ=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵四边形ABCD是矩形,
∴四边形ABHP是矩形,
∴PH=AB=3,
又∵EC=BC﹣BE=5﹣2=3,
∴PH=EC,
∴△PHE≌ECQ(ASA),
∴PE=QE,
∴△PQE 是等腰直角三角形;
(4)①如图所示,当点P在BE上时,
∵QE=QF=3,AQ=BE=2,
在Rt△AQF中,,
则 ,
∵PE=t,
∴BP=2﹣t,PF=PE=t,
在Rt△PBF中,PF2=PB2+FB2,
∴,
解得:,
当 时,点F在矩形内部,
∴0<t符合题意.
②当P点在AB上时,当F,A重合时符合题意,此时如图,
则PB=t﹣BE=t﹣2,PE=AP=AB﹣PB=3﹣(t﹣2)=5﹣t,
在Rt△PBE中,PE2=PB2+BE2,
∴(5﹣t)2=(t﹣2)2+22,
解得t.
③当点P在AD上,当F,D重合时,此时点Q与点C重合,则PFQE是正方形,此时t=2+3+2=7.
综上所述,0<t或t或t=7.
10.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠HAB=∠ABC,
∵点G是AB的中点,
∴AG=BG,
又∵∠AGH=∠BGC,
∴△AGH≌△BGC(AAS);
(2)解:∵四边形ABCD是菱形,
∴AO=CO,BO=DO,AC⊥BD,∠ABD∠ABC=30°,
∴AOAB=3,BOAO=3,
∴BD=6;
(3)解:当∠PAD=90°时,
∵四边形ABCD是菱形,
∴∠ABC=∠ADC=60°,∠ADB∠ADC=30°,
∴ADAP=6,PD=2AP,
∴AP=2,DP=4,
∴BP=2,
∵AD∥BC,
∴△BPC∽△DPH,
∴,
∴2;
当∠APH=90°时,
∴∠DPA=∠DPC=45°,
∴AO=PO=3,
∴BP=33,DP=33,
∵AD∥BC,
∴△BPC∽△DPH,
∴,
∴2;
综上所述:2或2;
(4)解:∠CGN的度数是定值,
如图,取BC的中点H,连接OH,HM,NC,
∵MN是CG的垂直平分线,
∴GN=CN,GM=CM,
∴∠NGC=∠GCN,
又∵点H是BC的中点,
∴MH∥AB,
∵点H是BC的中点,AO=CO,
∴OH∥AB,
∴点M,点H,点O三点共线,
∵点H是BC的中点,AC⊥BD,
∴HO=HB=CH,
∴∠CBO=∠BOH=30°,
∵∠COB=∠NMC=90°,
∴点O,点C,点M,点N四点共圆,
∴∠BOH=∠NCM=30°,
∴∠CGN=∠NCM=30°.
11.【解答】(1)证明:∵四边形ABCD为矩形,
.∴AD∥BF,
∴∠D=∠DCF,
∵G为CD中点,
∴DG=CG,
∵∠AGD=∠FGC,
∴△ADG≌△FCG(ASA);
(2)解:∵四边形ABCD为矩形,
∴∠ABC=90°,
∵CE⊥AF,
∴∠CEF=90°=∠ABC,
∵∠F=∠F,
∴△CEF∽△ABF,
∴,
∵AB=4,BF=x,
在Rt△ABF中,AF,
∵CE=y,
∴,
∴y(或者y);
(3)解:过点E作EN⊥BF于点N,
∵四边形ABCD为矩形,AD=3,
∴AD=BC=3,
∵AB=4,CF=1,
∴AB=BF,
∴△ABF为等腰直角三角形,
∴∠CFE=∠BAF=45°,
∵CE⊥AF,
∴△CEF为等腰直角三角形,
∴∠ECF=45°,
∵EN⊥CF,
∴EN平分CF,
∴CN=NF=NE,
在Rt△BNE中,根据勾股定理得:
BE2=BN2+EN2,
∴BE,
∵∠ECF=∠BAF=45°,
∴∠BAM=∠BCE=135°,
∵BM⊥BE,
∴∠MBA+∠ABE=90°,
∠ABE+∠EBC=90°,
∴∠MBA=∠EBC,
∴△BAM∽△BCE,
∴,
∴,
∴BM.
12.【解答】(1)证明:∵AC是正方形ABCD的对角线,
∴AB=AD,∠BAE=∠DAE=45°,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)解:①△FBG为等腰三角形,理由:
∵四边形ABCD是正方形,
∴∠GAD=90°,
∴∠AGD+∠ADG=90°,
由(1)知,△ABE≌△ADE,
∴∠ADG=∠EBG,
∴∠AGD+∠EBG=90°,
∵FB⊥BE,
∴∠FBG+∠EBG=90°,
∴∠AGD=∠FBG,
∵∠AGD=∠FGB,
∴∠FBG=∠FGB,
∴FG=FB,
∴△FBG是等腰三角形;
②如图,过点F作FH⊥AB于H,
∵四边形ABCD为正方形,点G为AB的中点,AB=4,
∴AG=BG=2,AD=4,
由①知,FG=FB,
∴GH=BH=1,
∴AH=AG+GH=3,
在Rt△FHG与Rt△DAG中,∵∠FGH=∠DGA,
∴tan∠FGH=tan∠DGA,
∴2,
∴FH=2GH=2,
在Rt△AHF中,AF;
(3)∵FB⊥BE,
∴∠FBE=90°,
在Rt△EBF中,BE=BF,
∴EFBE,
由(1)知,BE=DE,
由(2)知,FG=BF,
∴GE=EF﹣FGBE﹣BFDE﹣DE=(1)DE.
13.【解答】(1)解:∵四边形ABCD是矩形,
∴∠DAB=∠B=∠ADC=90°,CD=AB=10,BC=AD=8,
在Rt△BCF中,CF=CD=10,BC=8,
∴BF=6,
∴AF=AB﹣BF=4,
设AE=x,则EF=DE=8﹣x,
在Rt△AEF中,由勾股定理得,
EF2﹣AE2=AF2,
∴(8﹣x)2﹣x2=42,
∴x=3,
∴AE=3;
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴△AGE∽△DCE,
∴,
由(1)得:AE=3,
∴DE=8﹣3=5,
∴,
∴AG=6,
∴FG=AF+AG=4+6=10,
∴FG=CD,
∴四边形DGFC是平行四边形,
∵CD=CF,
∴ DGFC是菱形;
(3)解:∵四边形FGDC是菱形,
∴∠DGC=∠DCG=∠FGC,DG=CD=10,
在Rt△BCG中,BC=8,BG=BF+FG=6+10=16,
∴tan∠FGC,CG8,
∴sin∠FCG,
如图1,
当∠MDN=90°时,
在Rt△GDM中,
DM=DG tan∠DGM=10 tan∠FGC=105,
在Rt△DMN中,
DN=DM tan∠DMN,
∵∠DMN=∠DCM,∠DCM=∠FGC,
∴DN=DM tan∠FGC=5,
如图2,
当∠MND=90°时,∠DMN+∠GDM=90°,
∵∠DMN=∠DCM=∠DGM,
∴∠DGM+∠GDM=90°,
∴∠DMG=90°,
∴DM=DG sin∠DGM=102,
在Rt△DMN中,
DN=DM sin∠DMN=DM sin∠FGC=22,
综上所述:DN或2.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°.
∵DE=DF,∠EDF=90°.
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS);
(2)①证明:如图2中,设AG与CD相交于点P.
∵∠ADP=90°,
∴∠DAP+∠DPA=90°.
∵△ADE≌△CDF,
∴∠DAE=∠DCF.
∵∠DPA=∠GPC,
∴∠DAE+∠DPA=∠GPC+∠GCP=90°.
∴∠PGN=90°,
∵BM⊥AG,BN⊥GN,
∴四边形BMGN是矩形,
∴∠MBN=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠MBN=90°.
∴∠ABM=∠CBN.
又∵∠AMB=∠BNC=90°,
∴△AMB≌△CNB.
∴MB=NB.
∴矩形BMGN是正方形;
②解:作DH⊥AG交AG于点H,作BM⊥AG于点M,
此时△AMB≌△AHD.
∴BM=AH.
∵AH2=AD2﹣DH2,AD=4,
∴DH最大时,AH最小,DH最大值=DE=2.
∴BM最小值=AH最小值.
由(2)①可知,△BGM是等腰直角三角形,
∴BG最小值.
15.【解答】(1)证明:如图1,∵四边形ABCD是菱形,
∴CB=AB,CD=AD,
∵BD=BD,
∴△ABD≌△CBD,
∴∠CBD=∠ABD∠ABC,
∵∠CBG=∠EBG∠EBC,
∴∠DBG=∠CBD+∠CBG(∠ABC+∠EBC)180°=90°.
(2)解:①如图2,连结AC交BD于点K,交DE于点L,
∵AC⊥BD,
∴∠AKB=90°,
∵AB=5,BD=6,
∴BK=DKBD=3,
∴AK4,
∴CK=AK=4,
∴AC=8,
∴S菱形ABCDAC BD8×6=24.
②∵∠DKL=∠DBG=90°,
∴AC∥BG,
∴1,
∴DL=GLDG,
∵DG=2GE,
∴GEDG,
∴DL=GL=GE,
∵CD∥AB,
∴,
∴CLAC8,
∴KL=4,
∴tan∠BDE.
(3)解:如图3,过点G作GT∥BC,交AE于点T,则GT为定值,
理由:连结AC交BD于点K,交DE于点L,
∵∠DKL=∠DBG=90°,
∴当∠DAB的大小发生变化时,始终都有BG∥AC,
∴△BGE∽△ALE,
∵BE=AB,
∴1,
∴EG=LG,
∵KL∥BG,
∴1,
∴DL=LG=EGED,
∵AD∥BC,
∴GT∥AD,
∴△ETG∽△EAD,
∴,
∵BE=AB=DA=5,
∴GTDA5,
∴GT为定值;
∵EA=BE+AB=10,
∴ETEA10.
16.【解答】(1)证明:如图1中,作FM⊥AC,垂足为M,
∵四边形ABCD是矩形,
∴∠B=90°,
∵FM⊥AC,
∴∠B=∠AMF=90°,
∵∠BAC=∠EAF,
∴∠BAE=∠MAF,
在△ABE和△AMF中,
,
∴△ABE≌△AMF(AAS),
∴AB=AM;
(2)解:当点E在BC上,在Rt△ABE中,AB=4,AE=3,
∴BE,
∵△ABE≌△AMF,
∴AB=AM=4,FM=BE,
在Rt△ABC中,AB=4,BC=3,
∴AC5,
∴CM=AC﹣AM=5﹣4=1,
∵∠CMF=90°,
∴CF.
当点E在CD上时,作FH⊥AC于点H,可证DE=AD=AH=FH=3,CH=2,
可得CF.
综上所述,CF的值为或;
(3)解:当点E在BC上时,如图2中,过点D作DH⊥FM于点H.
∵△ABE≌△AMF,
∴AM=AB=4,
∵∠AMF=90°,
∴点F在射线FM上运动,当点F与K重合时,DF的值最小,
∵∠CMJ=∠ADC=90°,∠MCJ=∠ACD,
∴△CMJ∽△CDA,
∴,
∴,
∴MJ,CJ,
∴DJ=CD﹣CJ=4,
∵∠CMJ=∠DHJ=90°,∠CJM=∠DJH,
∴△CMJ∽△DHJ,
∴,
∴,
∴DH,
∴DF的最小值为.
当点E在线段CD上时,如图3中,将线段AD绕点A顺时针旋转,旋转角为∠BAC,得到线段AR,连接FR,过点D作DQ⊥AR于点Q,DK⊥FR于点K.
∵∠EAF=∠BAC,∠DAR=∠BAC,
∴∠DAE=∠RAF,
∵AE=AF,AD=AR,
∴△ADE≌△ARF(SAS),
∴∠ADE=∠ARF=90°,
∴点F在直线RF上运动,当点D与K重合时,DF的值最小,
∵DQ⊥AR,DK⊥RF,
∴∠R=∠DQR=∠DKR=90°,
∴四边形DKRQ是矩形,
∴DK=QR,
∴AQ=AD cos∠BAC=3,
∵AR=AD=3,
∴DK=QR=AR﹣AQ,
∴DF的最小值为,
∵,
∴DF的最小值为.
解法二:当点E在BC上时,如图,将线段AD绕点A逆时针旋转,旋转角的度数=∠BAC,得到AT,连接DT,ET,DF.
证明△DAF≌△TAE,推出DF=TE,
当TE⊥BC时,DF的值最小,可得DF的最小值为.
当点E在CD上时,同法可得DF的最小值为.
17.【解答】解:(1)线段AE,EF,BF组成的是直角三角形,理由如下:
∵AM=AC﹣CM=4﹣a,BN=4﹣b,
∴AE,BF,
∴AE2+BF2=2(4﹣a)2+2(4﹣b)2=2(a2+b2﹣8a﹣8b+32),
∵AB4,
∴EF=AB﹣AE﹣BF[4﹣(4﹣a)﹣(4﹣b)](a+b﹣4),
∵ab=8,
EF2=2(a+b﹣4)2=2(a2+b2﹣8a﹣8b+16+2ab)=2(a2+b2﹣8a﹣8b+32),
∴AE2+BF2=EF2,
∴线段AE,EF,BF组成的是直角三角形;
(2)①如图1,
连接PC交EF于G,
∵a=b,
∴ME=AM=BN=NF,
∵四边形CNPM是矩形,
∴矩形CNPM是正方形,
∴PC平分∠ACB,
∴CG⊥AB,
∴∠PGE=90°,
∵CM=CN=PM=PN,
∴PE=PF,
∵△AEM,△BNF,△PEF是等腰直角三角形,
EF2=AE2+BF2,EF2=PE2+PF2,
∴PE=AE=PF=BF,
∴ME=EG=FG=FN,
∴∠MCE=∠GCE,∠NCF=∠GCF,
∵∠ACB=90°,
∴∠ECG+∠FCG,
∴∠ECF=45°;
②如图2,
仍然成立,理由如下:
将△BCF逆时针旋转90°至△ACD,连接DE,
∴∠DAC=∠B=45°,AD=BF,
∴∠DAE=∠DAC+∠CAB=90°,
∴DE2=AD2+AE2=BF2+AE2
∵EF2=BF2+AE2,
∴DE=EF,
∵CD=CF,CE=CE,
∴△DCE≌△FCE(SSS),
∴∠ECF=∠DCE.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/3/15 10:19:43;用户:永州综合中专;邮箱:yzzh66@;学号:48626927
21世纪教育网(www.21cnjy.com)
同课章节目录
