2025年九年级中考数学三轮冲刺训练反比例函数与一次函数交点问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练反比例函数与一次函数交点问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 709.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 16:18:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练反比例函数与一次函数交点问题
一、选择题
1.如图是同一直角坐标系中函数y1=2x和的图象.观察图象可得不等式的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
2.反比例函数与一次函数的图形有一个交点,则k的值为( )
A.1 B.2 C. D.
3.如图,反比例函数与一次函数y=ax+b(a≠0)的图象相交于点A(1,3),B(c,﹣1),则k﹣a的值为( )
A.2 B.3 C.4 D.5
4.如图,反比例函数的图象与正比例函数y=﹣x的图象交于点A,C,过点A作AB⊥x轴,垂足为点B,连接BC,若S△ABC=2,则k的值为( )
A.4 B.2 C.﹣1 D.﹣2
5.如图,A,B是函数y=x与的图象的两个交点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AD,BC,则四边形ACBD的面积为( )
A.2 B.3 C.4 D.5
6.如图,在直角坐标系中,直线y=6﹣x与函数(x>0)的图象相交于点A、B,设A点的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别是( )
A.4,12 B.4,6 C.8,12 D.8,6
二、填空题
7.如图,平面直角坐标系内有两点A(4,0),B(0,4),若反比例函数的图象交线段AB于点C,D,且BC=CD,则k= .
8.如图,在平面直角坐标系中,直线与直线分别与函数的图象交点A、B两点,连接AB、OB,若△AOB的面积为12,则k的值为 .
9.如图,在平面直角坐标系中,直线y=kx+6与y轴交于点C,与反比例函数y在第一象限内的图象交于点B,连接OB,若S△OBC=9,tan∠BOC,则m的值是 .
10.如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 .
11.如图,一次函数y=2x与反比例函数y(k>0)的图象交于A,B两点,点M在以C(2,0)为圆心,半径为1的⊙C上,N是AM的中点,已知ON长的最大值为,则k的值是 .
12.如图,函数y(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:
①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;
③若M点的横坐标为1,△OAM为等边三角形,则k=2;
④若MFMB,则MD=2MA.其中正确的结论的序号是 .(只填序号)
三、解答题
13.如图,在平面直角坐标系中,一次函数的图象l与反比例函数y的图象交于M(,4),N(n,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)求△OMN的面积;
(3)若点P是y轴上一动点,连接PM,PN.当PM+PN的值最小时,求点P的坐标.
14.如图,在平面直角坐标系中,直线y=x+2与反比例函数的图象交于A、B两点,点A的横坐标为1.
(1)求k的值及点B的坐标.
(2)点P是线段AB上一点,点M在直线OB上运动,当时,求PM的最小值.
15.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2(m≠0)的图象相交于A(1,3),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出y1>y2时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求△ABC的面积.
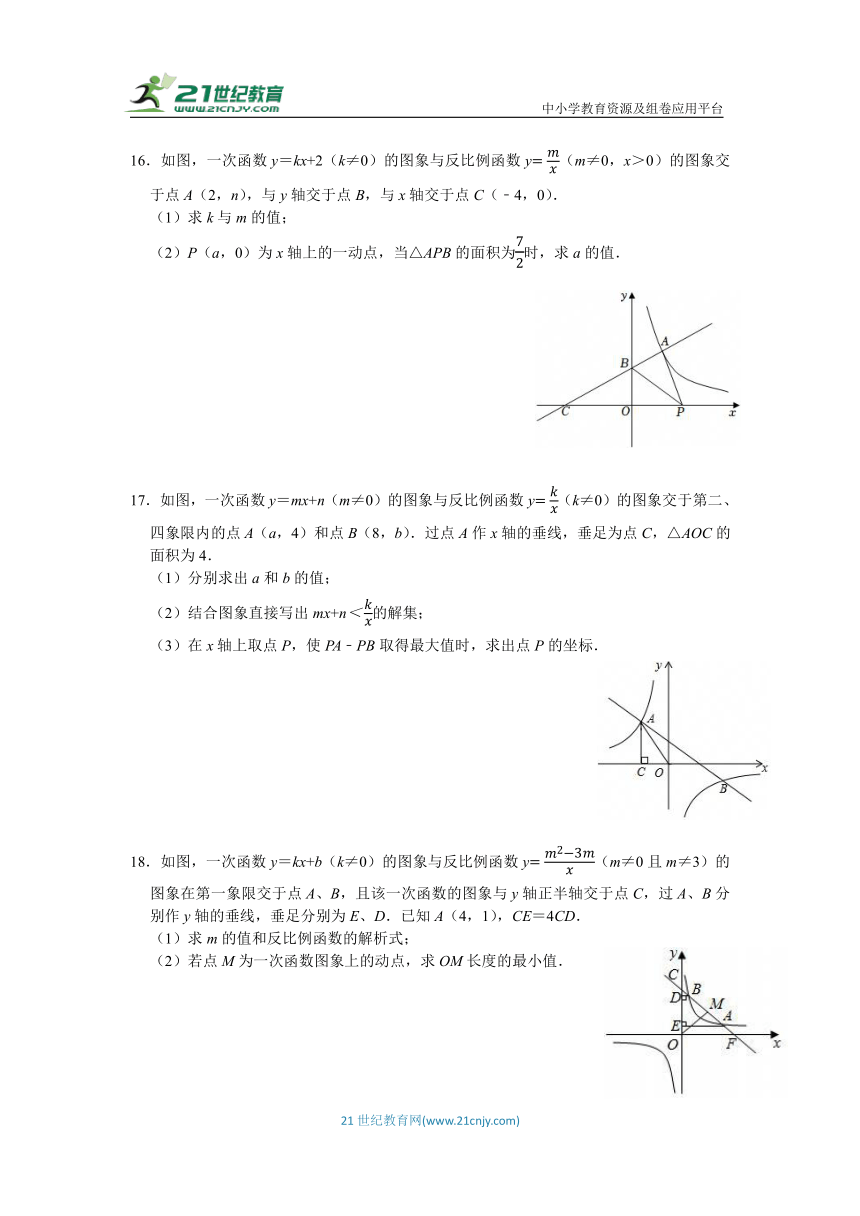
16.如图,一次函数y=kx+2(k≠0)的图象与反比例函数y(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
17.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,b).过点A作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n的解集;
(3)在x轴上取点P,使PA﹣PB取得最大值时,求出点P的坐标.
18.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0且m≠3)的图象在第一象限交于点A、B,且该一次函数的图象与y轴正半轴交于点C,过A、B分别作y轴的垂线,垂足分别为E、D.已知A(4,1),CE=4CD.
(1)求m的值和反比例函数的解析式;
(2)若点M为一次函数图象上的动点,求OM长度的最小值.
19.一次函数y=kx+b的图象经过点A(﹣2,12),B(8,﹣3).
(1)求该一次函数的解析式;
(2)如图,该一次函数的图象与反比例函数y(m>0)的图象相交于点C(x1,y1),D(x2,y2),与y轴交于点E,且CD=CE,求m的值.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 D C A D A A
1.【解答】解:由图象,函数y1=2x和的交点横坐标为﹣1,1,
∴当﹣1<x<0或x>1时,y1>y2,即,
故选:D.
2.【解答】解:把B(,m)代入,得m,
∴B点坐标为(,),
∵点B为反比例函数图象与一次函数图象的交点,
∴k.
故选:C.
3.【解答】解:∵点A(1,3)在反比例函数图象上,
∴k=1×3=3,
∴反比例函数解析式为y,
∵B(c,﹣1)在反比例函数图象上,
∴c=﹣3,
∴B(﹣3,﹣1),
∵A、B在一次函数图象上,
∴,解得,
∴k﹣a=3﹣1=2.
故选:A.
4.【解答】解:∵反比例函数的图象与正比例函数y=﹣x的图象交于点A,C,
∴OA=OC,
∵S△ABC=2,
∴S△AOBS△ABC2=1,
∵|k|=2S△AOB=2,图象在第二象限,
∴k=﹣2.
故选:D.
5.【解答】解:由对称性可知:OB=OA,OD=OC,
∴S△AOC、S△ODA、S△ODB、S△OBC的面积都等于,
∴四边形ABCD的面积为,
故选:A.
6.【解答】解:∵两函数图象的交点在第一象限,
∴x>0,y>0,
∴,
∴6﹣x,
∴x2﹣6x+4=0,
解得x=3±,
∵A在B的左边,
∴x=3,y=3,即A(3,3),
∴矩形的面积=(3)(3)=4;
矩形的周长=2(3)+2(3)=12.
故选:A.
二、填空题
7.【解答】解:设直线AB的解析式为y=kx+b,把代入点的坐标得到,
,
解得,
∴y=﹣x+4;
如图,过点C作CE⊥y轴于点E,过点D作DF⊥y轴于点F,
设点C的坐标为(t,﹣t+4),则CE=t,OE=﹣t+4,
∵BC=CD,
∴BD=BC+CD=2BC,
∵∠CBE=∠DBF,
∴△CBE∽△DBF,
∴,
即,
∴BF=2t,DF=2t,
∴OF=OB﹣BF=4﹣2t,
∴点D的坐标为(2t,4﹣2t),
∴t(﹣t+4)=2t(4﹣2t),
解得(不合题意,舍去),
∴点C的坐标为,
∴,
故答案为:.
8.【解答】解:如图,连接AC,
∵直线BC的解析式为直线,
∴C(0,4),
∵两条直线的k值相等,
∴AO∥BC,
∴S△AOB=S△AOC=12,
∴,
∴xA=﹣6,
将xA=﹣6代入正比例函数得,,
∴A(﹣6,4),
∵A(﹣6,4)在反比例函数图象上,
∴k=﹣24.
故答案为:﹣24.
9.【解答】解:∵直线y=kx+6与y轴交于点C,当x=0时,y=6,
∴点C的坐标为(0,6),
∴OC=6,
过B作BD⊥y轴于D,
由条件可知BD=3,
∵,
∴,
∴OD=9,
∴点B的坐标为(3,9),
∵反比例函数图象在第一象限内的图象经过点B,
∴m=3×9=27.
故答案为:27.
10.【解答】解:分别过A,B两点作x轴的垂线,垂足分别为E,F,
则△AEM∽△BFM.
又因为,
所以,
即AE=2BF.
令点B的坐标为(),
则点A的坐标为().
因为A,C关于原点对称,
所以点C坐标为().
连接OB,
因为△ABC的面积为24,
所以△BCO面积为12.
过点C作x轴的垂线,垂足为P,
由S△COP+S梯形CBFP=S△BCO+S△BOF,且S△COP=S△BOF得,
S梯形CBFP=S△BCO=12,
所以,
解得k=16.
故答案为:16.
11.【解答】解:方法一、联立,
∴,
∴,
∴A(),B(),
∴A与B关于原点O对称,
∴O是线段AB的中点,
∵N是线段AM的中点,
连接BM,则ON∥BM,且ON,
∵ON的最大值为,
∴BM的最大值为3,
∵M在⊙C上运动,
∴当B,C,M三点共线时,BM最大,
此时BC=BM﹣CM=2,
∴(,
∴k=0或,
∵k>0,
∴,
方法二、设点B(a,2a),
∵一次函数y=2x与反比例函数y(k>0)的图象交于A,B两点,
∴A与B关于原点O对称,
∴O是线段AB的中点,
∵N是线段AM的中点,
连接BM,则ON∥BM,且ON,
∵ON的最大值为,
∴BM的最大值为3,
∵M在⊙C上运动,
∴当B,C,M三点共线时,BM最大,
此时BC=BM﹣CM=2,
∴2,
∴a1或a2=0(不合题意舍去),
∴点B(,),
∴k,
故答案为:.
12.【解答】解:①设点A(m,),M(n,),
则直线AC的解析式为yx,
∴C(m+n,0),D(0,),
∴S△ODMn,S△OCA(m+n),
∴△ODM与△OCA的面积相等,故①正确;
∵反比例函数与正比例函数关于原点对称,
∴O是AB的中点,
∵BM⊥AM,
∴OM=OA,
∴k=mn,
∴A(m,n),M(n,m),
∴AM(m﹣n),OM,
∴AM不一定等于OM,
∴∠BAM不一定是60°,
∴∠MBA不一定是30°.故②错误,
∵M点的横坐标为1,
∴可以假设M(1,k),
∵△OAM为等边三角形,
∴OA=OM=AM,
1+k2=m2,
∵m>0,k>0,
∴m=k,
∵OM=AM,
∴(1﹣m)21+k2,
∴k2﹣4k+1=0,
∴k=2,
∵m>1,
∴k=2,故③正确,
如图,作MK∥OD交OA于K.
∵OF∥MK,
∴,
∴,
∵OA=OB,
∴,
∴,
∵KM∥OD,
∴2,
∴DM=2AM,故④正确.
故答案为①③④.
三、解答题
13.【解答】解:(1)由题意,∵M(,4)在反比例函数y上,
∴k4=2.
∴反比例函数表达式为y.
又N(n,1)在反比例函数y上,
∴n=2.
∴N(2,1).
设一次函数表达式为y=ax+b,
∴.
∴a=﹣2,b=5.
∴一次函数的表达式为y=﹣2x+5.
(2)由题意,如图,设直线l交x轴于点A,交y轴于点B,
又直线l为y=﹣2x+5,
∴A(,0),B(0,5).
∴OA,OB=5.
∴S△OMN=S△AOB﹣S△AON﹣S△BOMAO×BOAO yNBO×xM
515
.
(3)由题意,如图,作点M关于y轴的对称点M',连接M'N交y轴于点P,则PM+PN的最小值等于M'N的长.
∵M(,4)与M'关于y轴对称,
∴M'为(,4).
又N(2,1),
∴直线M′N为yx.
令x=0,则y,
∴P(0,).
14.【解答】解:(1)把x=1代入y=x+2,得出y=3,
∴A(1,3),
∴k=1×3=3,
∴反比例函数的解析式为y,
联立解析式得,
解得或,
∴B(﹣3,﹣1);
(2)∵,
∴P是AB的中点,
∴P(﹣1,1),
∴OB的解析式为yx,
当PM取得最小值时,PM⊥OB,
∴设直线PM的解析式为y=﹣3x+b,
代入p(﹣1,1)得3+b=1,
解得b=﹣2,
∴直线PM为y=﹣3x﹣2,
联立解析式得,
解得,
∴M(,),
∴PM的最小值为:.
15.【解答】解:(1)将点A坐标代入反比例函数解析式得,
m=1×3=3,
所以反比例函数解析式为y.
将点B坐标代入反比例函数解析式得,
n=﹣3,
所以点B的坐标为(﹣3,﹣1).
将A,B两点坐标代入一次函数解析式得,
,
解得,
所以一次函数解析式为y=x+2.
(2)由函数图象可知,
当﹣3<x<0或x>1时,一次函数的图象在反比例函数图象的上方,即y1>y2,
所以当y1>y2,x的取值范围是:﹣3<x<0或x>1.
(3)连接AO,令直线AB与x轴的交点为M,
将y=0代入y=x+2得,
x=﹣2,
所以点M的坐标为(﹣2,0),
所以S△AOB=S△AOM+S△BOM.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以BO=CO,
所以S△ABC=2S△AOB=8.
16.【解答】解:(1)把C(﹣4,0)代入y=kx+2,得k,
∴yx+2,
把A(2,n)代入yx+2,得n=3,
∴A(2,3),
把A(2,3)代入y,得m=6,
∴k,m=6;
(2)当x=0时,y=2,
∴B(0,2),
∵P(a,0)为x轴上的动点,
∴PC=|a+4|,
∴S△CBP PC OB|a+4|×2=|a+4|,S△CAPPC yA|a+4|×3,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或﹣11.
17.【解答】解:(1)∵点A(a,4),
∴AC=4,
∵S△AOC=4,即,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=﹣2 A(﹣2,4),
将A(﹣2,4)代入y得:k=﹣8,
∴反比例函数的关系式为:y,
把B(8,b)代入得:b=﹣1,
∴B(8,﹣1)
因此a=﹣2,b=﹣1;
(2)由图象可以看出mx+n的解集为:﹣2<x<0或x>8;
(3)如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
此时PA﹣PB最大(PA﹣PB=PA﹣PB′≤AB′,共线时差最大)
∵B(8,﹣1)
∴B′(8,1)
设直线AP的关系式为y=mx+n,将 A(﹣2,4),B′(8,1)代入得:
,
解得:m,n,
∴直线AP的关系式为yx,
当y=0时,即x0,解得x,
∴P(,0).
18.【解答】解:(1)将点A(4,1)代入y,
得,m2﹣3m=4,
解得,m1=4,m2=﹣1,
∴m的值为4或﹣1;反比例函数解析式为:y;
(2)∵BD⊥y轴,AE⊥y轴,
∴∠CDB=∠CEA=90°,
∴△CDB∽△CEA,
∴,
∵CE=4CD,
∴AE=4BD,
∵A(4,1),
∴AE=4,
∴BD=1,
∴xB=1,
∴yB4,
∴B(1,4),
将A(4,1),B(1,4)代入y=kx+b,
得,,
解得,k=﹣1,b=5,
∴yAB=﹣x+5,
设直线AB与x轴交点为F,
当x=0时,y=5;当y=0时x=5,
∴C(0,5),F(5,0),
则OC=OF=5,
∴△OCF为等腰直角三角形,
∴CFOC=5,
则当OM垂直CF于M时,由垂线段最知可知,OM有最小值,
即OMCF.
19.【解答】解:(1)把点A(﹣2,12),B(8,﹣3)代入y=kx+b
得:
解得:
∴一次函数解析式为:y
(2)分别过点C、D做CA⊥y轴于点A,DB⊥y轴于点B
∵点C(x1,y1),D(x2,y2),
∴x1 y1=m,
由(1)点E坐标为(0,9),则AE=9﹣y1,
∵AC∥BD,CD=CE,
∴BD=2x1,EB=2(9﹣y1),
∴OB=9﹣2(9﹣y1)=2y1﹣9,
∴点D坐标为(2x1,2y1﹣9),
∴2x1 (2y1﹣9)=m,
整理得m=6x1,
∵x1 y1=m,
∴y1=6,
则点D坐标化为(2x1,3),
∵点D在y图象上
∴x1=2
∴m=x1 y1=12.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练反比例函数与一次函数交点问题
一、选择题
1.如图是同一直角坐标系中函数y1=2x和的图象.观察图象可得不等式的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
2.反比例函数与一次函数的图形有一个交点,则k的值为( )
A.1 B.2 C. D.
3.如图,反比例函数与一次函数y=ax+b(a≠0)的图象相交于点A(1,3),B(c,﹣1),则k﹣a的值为( )
A.2 B.3 C.4 D.5
4.如图,反比例函数的图象与正比例函数y=﹣x的图象交于点A,C,过点A作AB⊥x轴,垂足为点B,连接BC,若S△ABC=2,则k的值为( )
A.4 B.2 C.﹣1 D.﹣2
5.如图,A,B是函数y=x与的图象的两个交点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AD,BC,则四边形ACBD的面积为( )
A.2 B.3 C.4 D.5
6.如图,在直角坐标系中,直线y=6﹣x与函数(x>0)的图象相交于点A、B,设A点的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别是( )
A.4,12 B.4,6 C.8,12 D.8,6
二、填空题
7.如图,平面直角坐标系内有两点A(4,0),B(0,4),若反比例函数的图象交线段AB于点C,D,且BC=CD,则k= .
8.如图,在平面直角坐标系中,直线与直线分别与函数的图象交点A、B两点,连接AB、OB,若△AOB的面积为12,则k的值为 .
9.如图,在平面直角坐标系中,直线y=kx+6与y轴交于点C,与反比例函数y在第一象限内的图象交于点B,连接OB,若S△OBC=9,tan∠BOC,则m的值是 .
10.如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 .
11.如图,一次函数y=2x与反比例函数y(k>0)的图象交于A,B两点,点M在以C(2,0)为圆心,半径为1的⊙C上,N是AM的中点,已知ON长的最大值为,则k的值是 .
12.如图,函数y(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:
①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;
③若M点的横坐标为1,△OAM为等边三角形,则k=2;
④若MFMB,则MD=2MA.其中正确的结论的序号是 .(只填序号)
三、解答题
13.如图,在平面直角坐标系中,一次函数的图象l与反比例函数y的图象交于M(,4),N(n,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)求△OMN的面积;
(3)若点P是y轴上一动点,连接PM,PN.当PM+PN的值最小时,求点P的坐标.
14.如图,在平面直角坐标系中,直线y=x+2与反比例函数的图象交于A、B两点,点A的横坐标为1.
(1)求k的值及点B的坐标.
(2)点P是线段AB上一点,点M在直线OB上运动,当时,求PM的最小值.
15.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2(m≠0)的图象相交于A(1,3),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出y1>y2时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求△ABC的面积.
16.如图,一次函数y=kx+2(k≠0)的图象与反比例函数y(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
17.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,b).过点A作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n的解集;
(3)在x轴上取点P,使PA﹣PB取得最大值时,求出点P的坐标.
18.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0且m≠3)的图象在第一象限交于点A、B,且该一次函数的图象与y轴正半轴交于点C,过A、B分别作y轴的垂线,垂足分别为E、D.已知A(4,1),CE=4CD.
(1)求m的值和反比例函数的解析式;
(2)若点M为一次函数图象上的动点,求OM长度的最小值.
19.一次函数y=kx+b的图象经过点A(﹣2,12),B(8,﹣3).
(1)求该一次函数的解析式;
(2)如图,该一次函数的图象与反比例函数y(m>0)的图象相交于点C(x1,y1),D(x2,y2),与y轴交于点E,且CD=CE,求m的值.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 D C A D A A
1.【解答】解:由图象,函数y1=2x和的交点横坐标为﹣1,1,
∴当﹣1<x<0或x>1时,y1>y2,即,
故选:D.
2.【解答】解:把B(,m)代入,得m,
∴B点坐标为(,),
∵点B为反比例函数图象与一次函数图象的交点,
∴k.
故选:C.
3.【解答】解:∵点A(1,3)在反比例函数图象上,
∴k=1×3=3,
∴反比例函数解析式为y,
∵B(c,﹣1)在反比例函数图象上,
∴c=﹣3,
∴B(﹣3,﹣1),
∵A、B在一次函数图象上,
∴,解得,
∴k﹣a=3﹣1=2.
故选:A.
4.【解答】解:∵反比例函数的图象与正比例函数y=﹣x的图象交于点A,C,
∴OA=OC,
∵S△ABC=2,
∴S△AOBS△ABC2=1,
∵|k|=2S△AOB=2,图象在第二象限,
∴k=﹣2.
故选:D.
5.【解答】解:由对称性可知:OB=OA,OD=OC,
∴S△AOC、S△ODA、S△ODB、S△OBC的面积都等于,
∴四边形ABCD的面积为,
故选:A.
6.【解答】解:∵两函数图象的交点在第一象限,
∴x>0,y>0,
∴,
∴6﹣x,
∴x2﹣6x+4=0,
解得x=3±,
∵A在B的左边,
∴x=3,y=3,即A(3,3),
∴矩形的面积=(3)(3)=4;
矩形的周长=2(3)+2(3)=12.
故选:A.
二、填空题
7.【解答】解:设直线AB的解析式为y=kx+b,把代入点的坐标得到,
,
解得,
∴y=﹣x+4;
如图,过点C作CE⊥y轴于点E,过点D作DF⊥y轴于点F,
设点C的坐标为(t,﹣t+4),则CE=t,OE=﹣t+4,
∵BC=CD,
∴BD=BC+CD=2BC,
∵∠CBE=∠DBF,
∴△CBE∽△DBF,
∴,
即,
∴BF=2t,DF=2t,
∴OF=OB﹣BF=4﹣2t,
∴点D的坐标为(2t,4﹣2t),
∴t(﹣t+4)=2t(4﹣2t),
解得(不合题意,舍去),
∴点C的坐标为,
∴,
故答案为:.
8.【解答】解:如图,连接AC,
∵直线BC的解析式为直线,
∴C(0,4),
∵两条直线的k值相等,
∴AO∥BC,
∴S△AOB=S△AOC=12,
∴,
∴xA=﹣6,
将xA=﹣6代入正比例函数得,,
∴A(﹣6,4),
∵A(﹣6,4)在反比例函数图象上,
∴k=﹣24.
故答案为:﹣24.
9.【解答】解:∵直线y=kx+6与y轴交于点C,当x=0时,y=6,
∴点C的坐标为(0,6),
∴OC=6,
过B作BD⊥y轴于D,
由条件可知BD=3,
∵,
∴,
∴OD=9,
∴点B的坐标为(3,9),
∵反比例函数图象在第一象限内的图象经过点B,
∴m=3×9=27.
故答案为:27.
10.【解答】解:分别过A,B两点作x轴的垂线,垂足分别为E,F,
则△AEM∽△BFM.
又因为,
所以,
即AE=2BF.
令点B的坐标为(),
则点A的坐标为().
因为A,C关于原点对称,
所以点C坐标为().
连接OB,
因为△ABC的面积为24,
所以△BCO面积为12.
过点C作x轴的垂线,垂足为P,
由S△COP+S梯形CBFP=S△BCO+S△BOF,且S△COP=S△BOF得,
S梯形CBFP=S△BCO=12,
所以,
解得k=16.
故答案为:16.
11.【解答】解:方法一、联立,
∴,
∴,
∴A(),B(),
∴A与B关于原点O对称,
∴O是线段AB的中点,
∵N是线段AM的中点,
连接BM,则ON∥BM,且ON,
∵ON的最大值为,
∴BM的最大值为3,
∵M在⊙C上运动,
∴当B,C,M三点共线时,BM最大,
此时BC=BM﹣CM=2,
∴(,
∴k=0或,
∵k>0,
∴,
方法二、设点B(a,2a),
∵一次函数y=2x与反比例函数y(k>0)的图象交于A,B两点,
∴A与B关于原点O对称,
∴O是线段AB的中点,
∵N是线段AM的中点,
连接BM,则ON∥BM,且ON,
∵ON的最大值为,
∴BM的最大值为3,
∵M在⊙C上运动,
∴当B,C,M三点共线时,BM最大,
此时BC=BM﹣CM=2,
∴2,
∴a1或a2=0(不合题意舍去),
∴点B(,),
∴k,
故答案为:.
12.【解答】解:①设点A(m,),M(n,),
则直线AC的解析式为yx,
∴C(m+n,0),D(0,),
∴S△ODMn,S△OCA(m+n),
∴△ODM与△OCA的面积相等,故①正确;
∵反比例函数与正比例函数关于原点对称,
∴O是AB的中点,
∵BM⊥AM,
∴OM=OA,
∴k=mn,
∴A(m,n),M(n,m),
∴AM(m﹣n),OM,
∴AM不一定等于OM,
∴∠BAM不一定是60°,
∴∠MBA不一定是30°.故②错误,
∵M点的横坐标为1,
∴可以假设M(1,k),
∵△OAM为等边三角形,
∴OA=OM=AM,
1+k2=m2,
∵m>0,k>0,
∴m=k,
∵OM=AM,
∴(1﹣m)21+k2,
∴k2﹣4k+1=0,
∴k=2,
∵m>1,
∴k=2,故③正确,
如图,作MK∥OD交OA于K.
∵OF∥MK,
∴,
∴,
∵OA=OB,
∴,
∴,
∵KM∥OD,
∴2,
∴DM=2AM,故④正确.
故答案为①③④.
三、解答题
13.【解答】解:(1)由题意,∵M(,4)在反比例函数y上,
∴k4=2.
∴反比例函数表达式为y.
又N(n,1)在反比例函数y上,
∴n=2.
∴N(2,1).
设一次函数表达式为y=ax+b,
∴.
∴a=﹣2,b=5.
∴一次函数的表达式为y=﹣2x+5.
(2)由题意,如图,设直线l交x轴于点A,交y轴于点B,
又直线l为y=﹣2x+5,
∴A(,0),B(0,5).
∴OA,OB=5.
∴S△OMN=S△AOB﹣S△AON﹣S△BOMAO×BOAO yNBO×xM
515
.
(3)由题意,如图,作点M关于y轴的对称点M',连接M'N交y轴于点P,则PM+PN的最小值等于M'N的长.
∵M(,4)与M'关于y轴对称,
∴M'为(,4).
又N(2,1),
∴直线M′N为yx.
令x=0,则y,
∴P(0,).
14.【解答】解:(1)把x=1代入y=x+2,得出y=3,
∴A(1,3),
∴k=1×3=3,
∴反比例函数的解析式为y,
联立解析式得,
解得或,
∴B(﹣3,﹣1);
(2)∵,
∴P是AB的中点,
∴P(﹣1,1),
∴OB的解析式为yx,
当PM取得最小值时,PM⊥OB,
∴设直线PM的解析式为y=﹣3x+b,
代入p(﹣1,1)得3+b=1,
解得b=﹣2,
∴直线PM为y=﹣3x﹣2,
联立解析式得,
解得,
∴M(,),
∴PM的最小值为:.
15.【解答】解:(1)将点A坐标代入反比例函数解析式得,
m=1×3=3,
所以反比例函数解析式为y.
将点B坐标代入反比例函数解析式得,
n=﹣3,
所以点B的坐标为(﹣3,﹣1).
将A,B两点坐标代入一次函数解析式得,
,
解得,
所以一次函数解析式为y=x+2.
(2)由函数图象可知,
当﹣3<x<0或x>1时,一次函数的图象在反比例函数图象的上方,即y1>y2,
所以当y1>y2,x的取值范围是:﹣3<x<0或x>1.
(3)连接AO,令直线AB与x轴的交点为M,
将y=0代入y=x+2得,
x=﹣2,
所以点M的坐标为(﹣2,0),
所以S△AOB=S△AOM+S△BOM.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以BO=CO,
所以S△ABC=2S△AOB=8.
16.【解答】解:(1)把C(﹣4,0)代入y=kx+2,得k,
∴yx+2,
把A(2,n)代入yx+2,得n=3,
∴A(2,3),
把A(2,3)代入y,得m=6,
∴k,m=6;
(2)当x=0时,y=2,
∴B(0,2),
∵P(a,0)为x轴上的动点,
∴PC=|a+4|,
∴S△CBP PC OB|a+4|×2=|a+4|,S△CAPPC yA|a+4|×3,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或﹣11.
17.【解答】解:(1)∵点A(a,4),
∴AC=4,
∵S△AOC=4,即,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=﹣2 A(﹣2,4),
将A(﹣2,4)代入y得:k=﹣8,
∴反比例函数的关系式为:y,
把B(8,b)代入得:b=﹣1,
∴B(8,﹣1)
因此a=﹣2,b=﹣1;
(2)由图象可以看出mx+n的解集为:﹣2<x<0或x>8;
(3)如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
此时PA﹣PB最大(PA﹣PB=PA﹣PB′≤AB′,共线时差最大)
∵B(8,﹣1)
∴B′(8,1)
设直线AP的关系式为y=mx+n,将 A(﹣2,4),B′(8,1)代入得:
,
解得:m,n,
∴直线AP的关系式为yx,
当y=0时,即x0,解得x,
∴P(,0).
18.【解答】解:(1)将点A(4,1)代入y,
得,m2﹣3m=4,
解得,m1=4,m2=﹣1,
∴m的值为4或﹣1;反比例函数解析式为:y;
(2)∵BD⊥y轴,AE⊥y轴,
∴∠CDB=∠CEA=90°,
∴△CDB∽△CEA,
∴,
∵CE=4CD,
∴AE=4BD,
∵A(4,1),
∴AE=4,
∴BD=1,
∴xB=1,
∴yB4,
∴B(1,4),
将A(4,1),B(1,4)代入y=kx+b,
得,,
解得,k=﹣1,b=5,
∴yAB=﹣x+5,
设直线AB与x轴交点为F,
当x=0时,y=5;当y=0时x=5,
∴C(0,5),F(5,0),
则OC=OF=5,
∴△OCF为等腰直角三角形,
∴CFOC=5,
则当OM垂直CF于M时,由垂线段最知可知,OM有最小值,
即OMCF.
19.【解答】解:(1)把点A(﹣2,12),B(8,﹣3)代入y=kx+b
得:
解得:
∴一次函数解析式为:y
(2)分别过点C、D做CA⊥y轴于点A,DB⊥y轴于点B
∵点C(x1,y1),D(x2,y2),
∴x1 y1=m,
由(1)点E坐标为(0,9),则AE=9﹣y1,
∵AC∥BD,CD=CE,
∴BD=2x1,EB=2(9﹣y1),
∴OB=9﹣2(9﹣y1)=2y1﹣9,
∴点D坐标为(2x1,2y1﹣9),
∴2x1 (2y1﹣9)=m,
整理得m=6x1,
∵x1 y1=m,
∴y1=6,
则点D坐标化为(2x1,3),
∵点D在y图象上
∴x1=2
∴m=x1 y1=12.
21世纪教育网(www.21cnjy.com)
同课章节目录
