2025年九年级中考数学三轮冲刺训练二次函数压轴题训练(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练二次函数压轴题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 16:20:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练二次函数压轴题训练
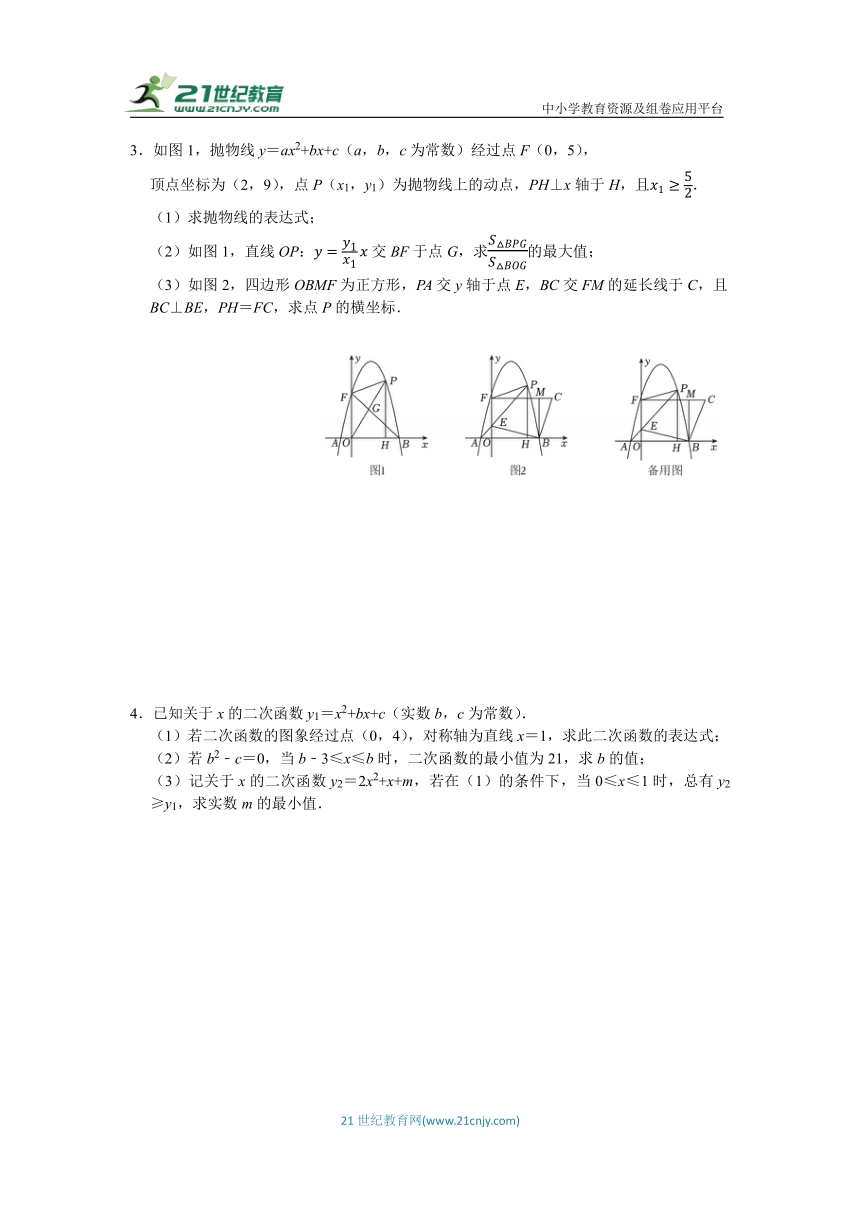
1.如图,抛物线y=x2+bx+c过点A(﹣1,0)、点B(5,0),交y轴于点C.
(1)求b,c的值.
(2)点P(x0,y0)(0<x0<5)是抛物线上的动点.
①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;
②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
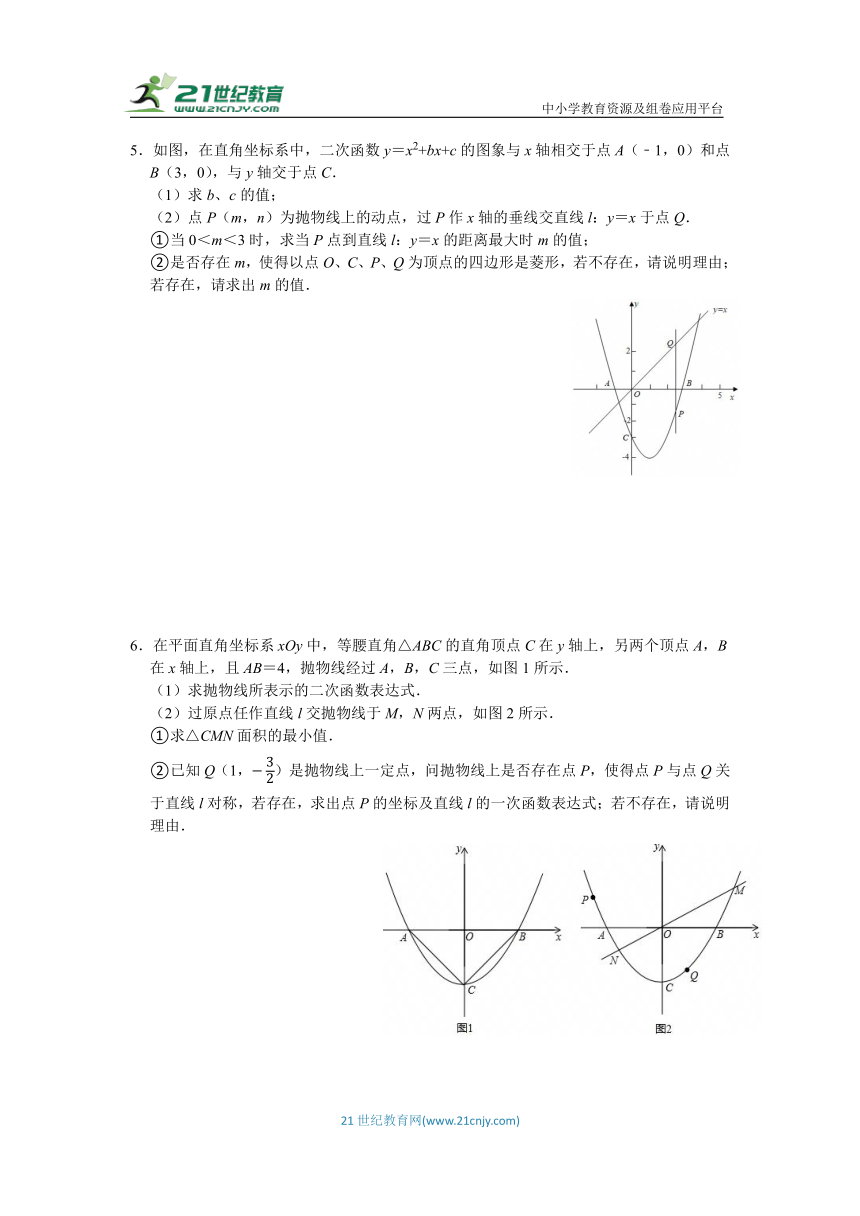
2.如图,二次函数的图象与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C,顶点为D.O为坐标原点,.
(1)求二次函数的表达式;
(2)求四边形ACDB的面积;
(3)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.
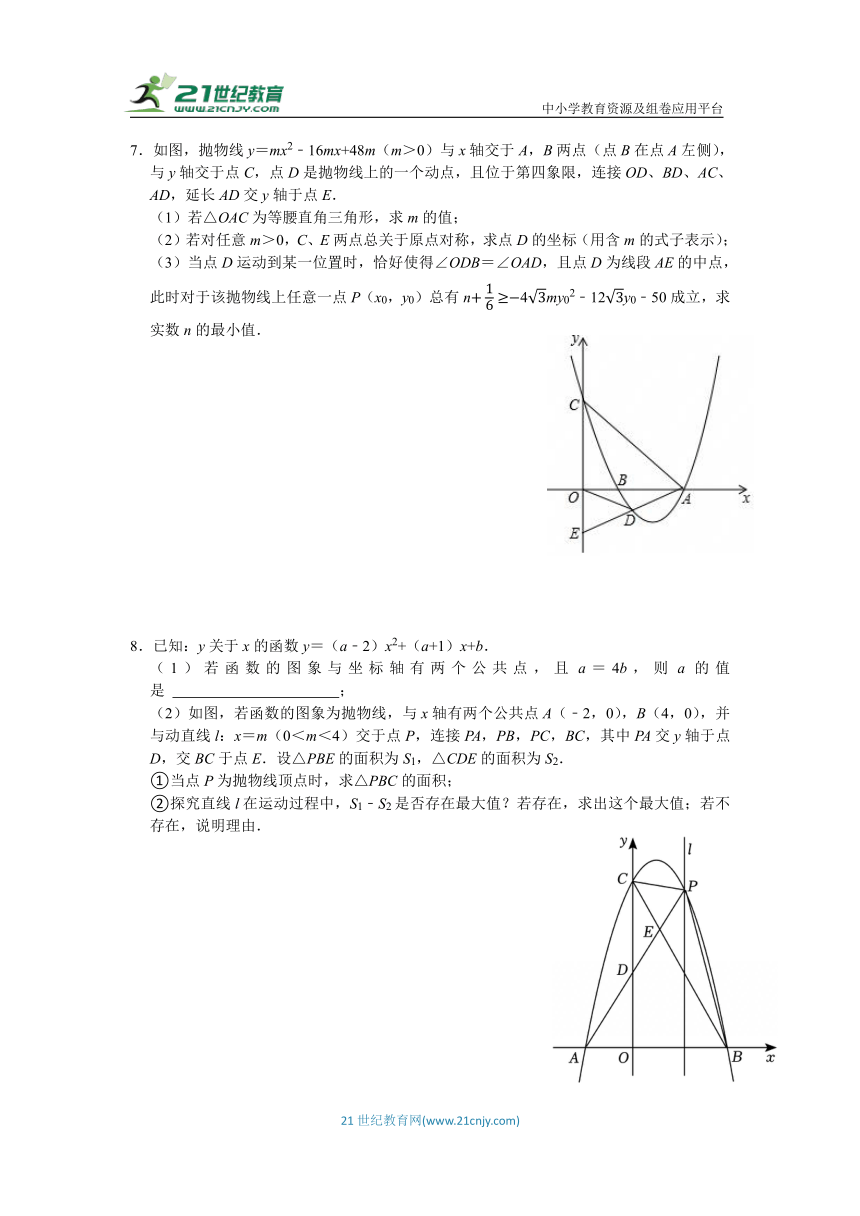
3.如图1,抛物线y=ax2+bx+c(a,b,c为常数)经过点F(0,5),
顶点坐标为(2,9),点P(x1,y1)为抛物线上的动点,PH⊥x轴于H,且.
(1)求抛物线的表达式;
(2)如图1,直线OP:交BF于点G,求的最大值;
(3)如图2,四边形OBMF为正方形,PA交y轴于点E,BC交FM的延长线于C,且BC⊥BE,PH=FC,求点P的横坐标.
4.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).
(1)若二次函数的图象经过点(0,4),对称轴为直线x=1,求此二次函数的表达式;
(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1,求实数m的最小值.
5.如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求b、c的值;
(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.
①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;
②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
6.在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
7.如图,抛物线y=mx2﹣16mx+48m(m>0)与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值;
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示);
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0,y0)总有n4my02﹣12y0﹣50成立,求实数n的最小值.
8.已知:y关于x的函数y=(a﹣2)x2+(a+1)x+b.
(1)若函数的图象与坐标轴有两个公共点,且a=4b,则a的值是 ;
(2)如图,若函数的图象为抛物线,与x轴有两个公共点A(﹣2,0),B(4,0),并与动直线l:x=m(0<m<4)交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为S1,△CDE的面积为S2.
①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,S1﹣S2是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
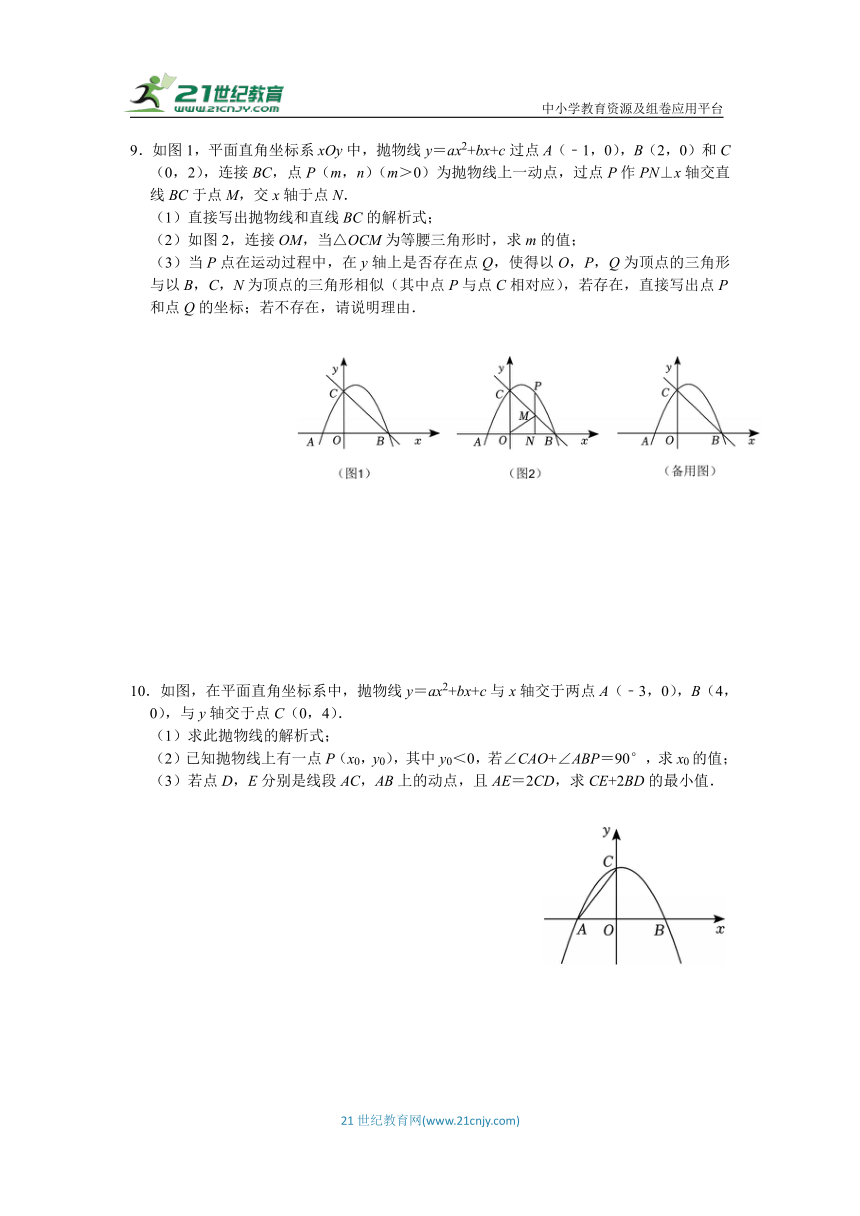
9.如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(﹣1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式;
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;
(3)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于两点A(﹣3,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)已知抛物线上有一点P(x0,y0),其中y0<0,若∠CAO+∠ABP=90°,求x0的值;
(3)若点D,E分别是线段AC,AB上的动点,且AE=2CD,求CE+2BD的最小值.
11.如图,抛物线yx2x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
12.已知抛物线y=ax2+bx+c过点A(﹣2,0),B(4,0),D(0,﹣8).
(1)求抛物线的解析式及顶点E的坐标;
(2)如图,抛物线y=ax2+bx+c向上平移,使顶点E落在x轴上的P点,此时的抛物线记为C,过P作两条互相垂直的直线与抛物线C交于不同于P的M,N两点(M位于N的右侧),过M,N分别作x轴的垂线交x轴于点M1,N1.
①求证:△PMM1∽△NPN1;
②设直线MN的方程为y=kx+m,求证:k+m为常数.
13.如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B,D(﹣4,5)两点,且与直线DC交于另一点E.
(1)求抛物线的解析式;
(2)F为抛物线对称轴上一点,Q为平面直角坐标系中的一点,是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由;
(3)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为M,连接ME,BP,探究EM+MP+PB是否存在最小值.若存在,请求出这个最小值及点M的坐标;若不存在,请说明理由.
14.如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,),与x轴交于A、B两点.
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.
(3)在(2)的条件下,点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.
(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
15.抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上一点,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案
1.【解答】解:(1)∵抛物线y=x2+bx+c过点A(﹣1,0)、点B(5,0),
∴抛物线的表达式为:y=(x+1)(x﹣5)=x2﹣4x﹣5,
∴b=﹣4,c=﹣5;
(2)由(1)得,抛物线的解析式为:y=x2﹣4x﹣5,
令x=0,则y=﹣5;
∴C(0,﹣5)
∴直线BC的表达式为:y=x﹣5,P(x0,4x0﹣5),
①如图,过点P作x轴的垂线,交线段BC于点D,
则D(x0,x0﹣5),
∴S△PBCOB PD5×(x0﹣54x0+5)
x0
(x0﹣2.5)2,
∴当x0=2.5时,S的值取最大,最大值为;
②存在,理由如下:
由题意可知,PE⊥PF,若△PEF是等腰直角三角形,则PE=PF,
由①可得,PE=x0﹣5﹣x02+4x0+55x0,
∵PF∥x轴,
∴F(4﹣x0,4x0﹣5),
∴PF=|2x0﹣4|,
∴|2x0﹣4|5x0,
解得x0=﹣1(舍)或x0=4或x0或x0(舍),
∴当△PEF是等腰直角三角形时,点P的坐标为(4,﹣5),(,).
2.【解答】解:(1)∵AO=1,tan∠ACO,
∴OC=5,即C的坐标为(0,5),
∵二次函数的图象与x轴交于A(﹣1,0),B(5,0)两点且过C的坐标(0,5),
设二次函数的解析式为y=ax2+bx+c,代入得:
,
解得:,
∴二次函数的解析式为y=﹣x2+4x+5;
(2)y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴顶点的坐标为(2,9),
过D作DN⊥AB于N,作DM⊥OC于M,
四边形ACDB的面积=S△AOC+S矩形OMDN﹣S△CDM+S△DNB
;
(3)如图,P是抛物线上的一点,且在第一象限,当∠ACO=∠PBC时,
连接PB,过C作CE⊥BC交BP于E,过E作EF⊥OC于F,
∵OC=OB=5,则BC=5,
∵∠ACO=∠PBC,
∴tan∠ACO=tan∠PBC,
即,
∴,
∵OC=OB,
∴∠OCB=45°,
∴∠ECF=180°﹣90°﹣45°=45°,
∴△EFC是等腰直角三角形,
∴FC=FE=1,
∴E的坐标为(1,6),
所以过B、E的直线的解析式为,
令,
解得,或,
所以BE直线与抛物线的两个交点为,
即所求P的坐标为.
3.【解答】解:(1)∵抛物线y=ax2+bx+c(a,b,c为常数)经过点F(0,5),顶点坐标为(2,9),
∴,
解得,
∴抛物线的表达式为y=﹣x2+4x+5;
(2)过点G作GT⊥x轴于点T,如图所示,
在y=﹣x2+4x+5中,令y=0得0=﹣x2+4x+5,
解得x=5或x=﹣1,
∴A(﹣1,0),B(5,0),
∵F(0,5),
∴BO=FO=5,
设直线BF的解析式为:y=kx+5,
∴y=5k+5,
解得k=﹣1,
∴直线BF的解析式为y=﹣x+5,
由G在直线BF上,设G(m,﹣m+5),
∵G在直线OP上,直线OP为,
∴﹣m+5m,
∴,
∴,
由P(x1,y1) 在抛物线 y=﹣x2+4x+5上,知P(x1,4x1+5),
∴,
∵S△BPG=S△BPO﹣S△BOG,
∴111,
∵,
∴111(x1)2,
∵,,
∴当 时,取最大值,最大值为;
(3)设MF交PH于T,如图:
∵OBFM为正方形,F(0,5),
∴FM=BM=OF=BO=5,∠MBO=90°,FC∥OB,
∵PH⊥x,∠MBO=90°,FC∥OB,
∴MTBH为矩形,
∴TH=MB=FM=5,
∵PH=FC,
∴PT=MC,
∵BC⊥BE,
∴∠MBC+∠MBE=90°,
∵∠MBO=90°,
∴∠OBE+∠MBE=90°,
∴∠OBE=∠MBC,
∴∠CMB=∠EOB=90°,
∴△EOB∽△CMB,
∴,
∵OB=MB,
∴EO=MC,
∵PH=FC,
∴PT=MC,
∴EO=MC=PT,
设 EO=MC=PT=a,
∴PH=PT+TH=5+a,E(0,a),
∵A(﹣1,0),
设直线AP的解析式为y=kx+b,
则,
∴,
∴直线AP的解析式为y=ax+a,
∵PH=a+5,P在直线AP上,
∴a+5=ax+a,
∴,即P点横坐标为 ,
∴x1,y1=a+5,
∴a,y15
∴54x1+5,
∴45=0,
∴(x1+1)(5x1+5)=0,
解得x1=1或x1或x1,
∵x1,
∴x1,
∴点P的横坐标为.
方法2:
设P(m,﹣m2+4m+5),
∴OH=m,PH=﹣m2+4m+5,
∵tan∠EAO,
∴,
∴EO=5﹣m,
∵BC⊥BE,
∴∠CBM=90°﹣∠MBE=∠EBO,
∵∠CMB=90°=∠EOB,BM=OB,
∴△CMB≌△EOB(ASA),
∴CM=EO=5﹣m,
∴CF=CM+FM=5﹣m+5=10﹣m,
∵PH=CF,
∴﹣m2+4m+5=10﹣m,
解得m或m,
∵m,
∴m,
∴点P的横坐标为.
4.【解答】解:(1)∵二次函数的图象经过点(0,4),
∴c=4;
∵对称轴为直线:x1,
∴b=﹣2,
∴此二次函数的表达式为:y1=x2﹣2x+4.
(2)当b2﹣c=0时,b2=c,此时函数的表达式为:y1=x2+bx+b2,
根据题意可知,需要分三种情况:
①当b,即b<0时,二次函数的最小值在x=b处取到;
∴b2+b2+b2=21,解得b1,b2(舍去);
②b﹣3,即b>2时,二次函数的最小值在x=b﹣3处取到;
∴(b﹣3)2+b(b﹣3)+b2=21,解得b3=4,b4=﹣1(舍去);
③b﹣3b,即0≤b≤2时,二次函数的最小值在x处取到;
∴()2+b ()+b2=21,解得b=±2(舍去).
综上所述,b的值为或4.
(3)由(1)知,二次函数的表达式为:y1=x2﹣2x+4,
设函数y3=y2﹣y1=x2+3x+m﹣4,
对称轴为直线x0,
∴当0≤x≤1时,y3随x的增大而增大,
∴当x=0时,y3即y2﹣y1有最小值m﹣4,
∴m﹣4≥0,
∴m≥4,即m的最小值为4.
5.【解答】解:(1)由二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),得:
,
解得:,
∴y=x2﹣2x﹣3,
∴b=﹣2,c=﹣3.
(2)①∵点P(m,n)在抛物线上y=x2﹣2x﹣3,
∴P(m,m2﹣2m﹣3),
∴PQ=m﹣(m2﹣2m﹣3)=﹣m2+3m+3=﹣(m)2,
∵过P作x轴的垂线交直线l:y=x于点Q,
∴Q(m,m),
设点P到直线y=x的距离为h,
∵直线y=x是一三象限的角平分线,
∴PQh,
∴当P点到直线l:y=x的距离最大时,PQ取得最大值,
∴当m时,PQ有最大值,
∴当P点到直线l:y=x的距离最大时,m的值为.
②∵抛物线与y轴交于点C,
∴x=0时,y=﹣3,
∴C(0,﹣3),
∵OC∥PQ,且以点O、C、P、Q为顶点的四边形是菱形,
∴PQ=OC,
又∵OC=3,PQ=|﹣m2+3m+3|,
∴3=|﹣m2+3m+3|,
解得:m1=0,m2=3,m3,m4,
当m1=0时,PQ与OC重合,菱形不成立,舍去;
当m2=3时,P(3,0),Q(3,3),
此时,四边形OCPQ是平行四边形,OQ,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m3时,Q(,),
此时,四边形OCQP是平行四边形,OQ,
∴CQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m4时,Q(,),
此时,四边形OCQP是平行四边形,OQ,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
综上所述:不存在m,使得以点O、C、P、Q为顶点的四边形是菱形.
6.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),
∴,
解得,,
∴抛物线的解析式为y2;
(2)①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由,可得,
∴x1+x2=2k,x1 x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②假设抛物线上存在点P(m,2),使得点P与点Q关于直线l对称,
∴OP=OQ,即,
解得,,,m3=1,m4=﹣1,
∵m3=1,m4=﹣1不合题意,舍去,
当时,点P(),
线段PQ的中点为(),
∴,
∴,
∴直线l的表达式为:y=(1)x,
当时,点P(,),
线段PQ的中点为(,﹣1),
∴,
∴,
∴直线l的解析式为y=(1)x.
综上,点P(,),直线l的解析式为y=(1)x或点P(,),直线l的解析式为y=(1)x.
7.【解答】解:(1)令y=mx2﹣16mx+48m=m(x﹣4)(x﹣12)=0,则x1=12,x2=4,
∴A(12,0),即OA=12,
又∵C(0,48m),
∴当△OAC为等腰直角三角形时,OA=OC,
即12=48m,
∴m;
(2)由(1)可知点C(0,48m),
∵对任意m>0,C、E两点总关于原点对称,
∴必有E(0,﹣48m),
设直线AE的解析式为y=kx+b,
将E(0,﹣48m),A(12,0)代入,可得
,解得,
∴直线AE的解析式为y=4mx﹣48m,
∵点D为直线AE与抛物线的交点,
∴解方程组,可得或(点A舍去),
即点D的坐标为(8,﹣16m);
(3)当∠ODB=∠OAD,∠DOB=∠AOD时,△ODB∽△OAD,
∴OD2=OA×OB=4×12=48,
∴OD=4,
又∵点D为线段AE的中点,
∴AE=2OD=8,
又∵OA=12,
∴OE4,
∴D(6,﹣2),
把D(6,﹣2)代入抛物线y=mx2﹣16mx+48m,可得﹣236m﹣96m+48m,
解得m,
∴抛物线的解析式为y(x﹣4)(x﹣12),
即y(x﹣8)2,
∵点P(x0,y0)为抛物线上任意一点,
∴y0,
令t=﹣4my02﹣12y0﹣50=﹣2y02﹣12y0﹣50=﹣2(y0+3)2+4,
则当y0时,t最大值=﹣2(3)2+4,
若要使n4my02﹣12y0﹣50成立,则n,
∴n≥3,
∴实数n的最小值为.
8.【解答】解:(1)①当a﹣2=0时,即a=2时,
y关于x的函数解析式为y=3x,
此时y=3x与x轴的交点坐标为(,0),
与y轴的交点坐标为(0,);
②当a﹣2≠0时,y关于x的函数为二次函数,
∵二次函数图象抛物线与坐标轴有两个交点,
∴抛物线可能存在与x轴有两个交点,其中一个交点为坐标原点或与x轴有一个交点与y轴一个交点两种情况.
当抛物线与x轴有两个交点且一个为坐标原点时,
由题意得b=0,此时a=0,抛物线为y=﹣2x2+x.
当y=0时,﹣2x2+x=0,
解得x1=0,x2.
∴其图象与x轴的交点坐标为(0,0)(,0).
当抛物线与x轴有一个交点与y轴有一个交点时,
由题意得,y=(a﹣2)x2+(a+1)x+b所对应的一元二次方程(a﹣2)x2+(a+1)x+b=0有两个相等实数根.
∴Δ=(a+1)2﹣4(a﹣2)a=0,
解得a,
此时yx2x,
当x=0时,y,
∴与y轴的交点坐标为(0,),
当y=0时,x2x0,
解得x1=x2,
∴与x轴的交点坐标为(,0),
综上所述,若y关于x的函数y=(a﹣2)x2+(a+1)x+b的图象与坐标轴有两个交点,则a可取的值为2,0,,
故答案为:2或0或;
(2)①如图,设直线l与BC交于点F,
根据题意得,
解得,
∴抛物线的解析式为y=﹣x2+2x+8,
当x=0时,y=8,
∴C(0,8),
∵y=﹣x2+2x+8=﹣(x﹣1)2+9,点P为抛物线顶点,
∴P(1,9),
∵B(4,0),C(0,8),
∴直线BC的解析式为y=﹣2x+8,
∴F(1,6),
∴PF=9﹣6=3,
∴△PBC的面积OB PF6;
②S1﹣S2存在最大值,
理由:如图,设直线x=m交x轴于H,
由①得,OB=4,AO=2,AB=6,OC=8,AH=2+m,P(m,﹣m2+2m+8),
∴PH=﹣m2+2m+8,
∵OD∥PH,
∴△AOD∽△AHP,
∴,
∴,
∴OD=8﹣2m,
∵S1﹣S2=S△PAB﹣S△AOD﹣S△OBC3m2+8m=﹣3(m)2,
∵﹣3<0,0<m<4,
∴当m时,S1﹣S2存在最大值,最大值为.
9.【解答】解:(1)∵抛物线y=ax2+bx+c过点A(﹣1,0),B(2,0),
∴抛物线的表达式为y=a(x+1)(x﹣2),
将点C(0,2)代入得,2=﹣2a,
∴a=﹣1,
∴抛物线的表达式为y=﹣(x+1)(x﹣2),即y=﹣x2+x+2.
设直线BC的表达式为y=kx+t,
将B(2,0),C(0,2)代入得,
,
解得,
∴直线BC的表达式为y=﹣x+2.
(2)∵点M在直线BC上,且P(m,n),
∴点M的坐标为(m,﹣m+2),
∴OC=2
∴CM2=(m﹣0)2+(﹣m+2﹣2)2=2m2,OM2=m2+(﹣m+2)2=2m2﹣4m+4,
当△OCM为等腰三角形时,
①若CM=OM,则CM2=OM2,
即2m2=2m2﹣4m+4,
解得m=1;
②若CM=OC,则CM2=OC2,
即2m2=4,
解得或m(舍去);
③若OM=OC,则OM2=OC2,
即2m2﹣4m+4=4,
解得m=2(舍)或m=0(舍去).
综上,m=1或m.
(3)∵点P与点C相对应,
∴△POQ∽△CBN或△POQ∽△CNB,
①若点P在点B的左侧,
则,
当△POQ∽△CBN,即∠POQ=45°时,
直线OP的表达式为y=x,
∴﹣m2+m+2=m,
解得或m(舍去),
∴,即OP=2,
∴,即,
解得OQ,
∴,
当△POQ∽△CNB,即∠PQO=45°时,
,
∴,即,
解得m=1±(舍去).
当△POQ∽△CNB,即∠PQO=45°时,
PQ,OQ=m﹣(﹣m2+m+2)=m2﹣2,
∴,即,
解得m,(负值舍去),
∴P(),Q(0.).
②若点P在点B的右侧,
则∠CBN=135°,BN=m﹣2,
当△POQ∽△CBN,即∠POQ=135°时,
直线OP的表达式为y=﹣x,
∴﹣m2+m+2=﹣m,
解得m=1或m=1(舍去),
∴,
∴,即,
解得OQ=1,
∴,
当△POQ∽△CNB,即∠PQO=135°时,
PQ,OQ=m2﹣2m﹣2,
∴,即,
解得m=1(舍)或m=1(舍去),
综上,P(),Q(0, )或P(),Q(0.)或P(),Q(0,)或.
10.【解答】解:(1)设抛物线的表达式为:y=a(x+3)(x﹣4)=a(x2﹣x﹣12),
即﹣12a=4,则a,
故抛物线的表达式为:yx2x+4①;
(2)在Rt△AOC中,tan∠CAO,
∵∠CAO+∠ABP=90°,
则tan∠ABP,
故设直线BP的表达式为:y(x﹣4)②,
联立①②得:x2x+4(x﹣4),
解得:xx0(不合题意的值已舍去);
(3)作∠EAG=∠BCD,
设AG=2BC=2×48,
∵AE=2CD,
∴△BCD∽△GAE且相似比为1:2,
则EG=2BD,
故当C、E、G共线时,CE+2BD=CE+EG=CG为最小,
在△ABC中,设AC边上的高为h,
则S△ABCAC hAB×CO,
即5h=4×7,
解得:h,
则sin∠ACBsin∠EAG,
则tan∠EAG=7,
过点G作GN⊥x轴于点N,
则NG=AG sin∠EAG,
即点G的纵坐标为:,
同理可得,点G的横坐标为:,
即点G(,),
由点C、G的坐标得,CG,
即CE+2BD的最小值为.
11.【解答】解:(1)令x=0,则y=4,
∴C(0,4);
令y=0,则x2x+4=0,
∴x=﹣2或x=3,
∴A(﹣2,0),B(3,0).
故答案为:(﹣2,0);(3,0);(0,4).
(2)①∵CP∥x轴,C(0,4),
∴P(1,4),
∴CP=1,AB=5,
∵CP∥x轴,
∴.
②如图,过点P作PQ∥AB交BC于点Q,
∴直线BC的解析式为:yx+4.
设点P的横坐标为m,
则P(m,m2m+4),Q(m2m,m2m+4).
∴PQ=m﹣(m2m)m2m,
∵PQ∥AB,
∴(m)2,
∴当m时,的最大值为.
另解:分别过点P,A作y轴的平行线,交直线BC于两点,仿照以上解法即可求解.
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.
过点C作CF∥x轴交抛物线于点F,
∵∠BCO+2∠PCB=90°,∠BCO+∠BCM+∠MCF=90°,
∴∠MCF=∠BCP,
延长CP交x轴于点M,
∵CF∥x轴,
∴∠PCF=∠BMC,
∴∠BCP=∠BMC,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,
∴M(8,0),
∴直线CM的解析式为:yx+4,
令x2x+4x+4,
解得x或x=0(舍),
∴存在点P满足题意,此时m.
12.【解答】(1)解:将A(﹣2,0),B(4,0),D(0,﹣8)代入y=ax2+bx+c,
∴,
解得,
∴y=x2﹣2x﹣8,
∵y=x2﹣2x﹣8=(x﹣1)2﹣9,
∴E(1,﹣9);
(2)①证明:∵PN⊥PM,
∴∠MPN=90°,
∴∠NPN1+∠MPM1=90°,
∵NN1⊥x轴,MM1⊥x轴,
∴∠NN1P=∠MM1P=90°,
∴∠N1PN+∠PNN1=90°,
∴∠MPM1=∠PNN1,
∴△PMM1∽△NPN1;
②证明:由题意可知平移后的抛物线解析式为y=(x﹣1)2,
设N(x1,kx1+m),M(x2,kx2+m),
联立方程组,
整理得x2﹣(2+k)x+1﹣m=0,
∴x1+x2=2+k,x1 x2=1﹣m,
∵△PMM1∽△NPN1,
∴,即,
∴k+m=(k+m)2,
∴k+m=1或k+m=0,
∵M、N与P不重合,
∴k+m=1,
∴k+m为常数.
13.【解答】解:(1)由点D的纵坐标知,正方形ABCD的边长为5,
则OB=AB﹣AO=5﹣4=1,故点B的坐标为(1,0),
则,解得,
故抛物线的表达式为y=x2+2x﹣3;
(2)存在,理由:
∵点D、E关于抛物线对称轴对称,故点E的坐标为(2,5),
由抛物线的表达式知,其对称轴为直线x=﹣1,故设点F的坐标为(﹣1,m),
由点B、E的坐标得,BE2=(2﹣1)2+(5﹣0)2=26,
设点Q的坐标为(s,t),
∵以点Q,F,E,B为顶点的四边形是以BE为边的菱形,
故点B向右平移1个单位向上平移5个单位得到点E,则Q(F)向右平移1个单位向上平移5个单位得到点F(Q),且BE=EF(BE=EQ),
则或,
解得或,
故点F的坐标为(﹣1,5)或(﹣1,5)或(﹣1,)或(﹣1,);
(3)存在,理由:
由题意抛物线的对称轴交x轴于点B′(﹣1,0),将点B′向左平移1个单位得到点B″(﹣2,0),
连接B″E,交函数的对称轴于点M,过点M作MP⊥y轴,则点P、M为所求点,此时EM+MP+PB为最小,
理由:∵B′B″=PM=1,且B′B″∥PM,故四边形B″B′PM为平行四边形,则B″M=B′P=BP,
则EM+MP+PB=EM+1+MB″=B″E+1为最小,
由点B″、E的坐标得,直线B″E的表达式为y(x+2),
当x=﹣1时,y(x+2),故点M的坐标为(﹣1,),
则EM+MP+PB的最小值B″E+1=11.
14.【解答】解:(1)由题可列方程组:,解得:
∴抛物线解析式为:yx2x﹣2;
(2)如图1,令y=0,可得x2x﹣2=0,
解得x=﹣1或3,
∴A(﹣1,0).B(3,0),C(0,﹣2),
∴AB=4,
∠AOC=90°,AC,AB=4,
设直线AC的解析式为:y=kx+b,则,解得:,
∴直线AC的解析式为:y=﹣2x﹣2;
当△AOC∽△AEB时
()2=()2,
∵S△AOC=1,∴S△AEB,
∴AB×|yE|,AB=4,则yE,
则点E(,);
由△AOC∽△AEB得:
∴;
(3)如图2,连接BF,过点F作FG⊥AC于G,
则FG=CFsin∠FCGCF,
∴CF+BF=GF+BF≥BE,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO
∴BE=ABcos∠ABE=ABcos∠ACO=4,
|y|=OBtan∠ABE=OBtan∠ACO=3,
∴当y时,即点F(0,),CF+BF有最小值为;
(4)①当点Q为直角顶点时(如图3):
由(3)易得F(0,),
∵C(0,﹣2)∴H(0,2)
设Q(1,m),过点Q作QM⊥y轴于点M.
则Rt△QHM∽Rt△FQM
∴QM2=HM FM,
∴12=(2﹣m)(m),
解得:m,
则点Q(1,)或(1,)
②当点H为直角顶点时:
点H(0,2),则点Q(1,2);
③当点F为直角顶点时:
同理可得:点Q(1,);
综上,点Q的坐标为:(1,)或(1,)或Q(1,2)或Q(1,).
15.【解答】解:(1)①将P(1,﹣3),B(4,0)代入y=ax2+c,得
,解得,
抛物线的解析式为yx2;
②如图1,
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为yx
解方程组得,.
∵P(1,﹣3),
∴D(,).
∴点D的坐标为(﹣1,﹣3)或(,).
(2)点P运动时,是定值,定值为2,理由如下:
作PQ⊥AB于Q点,设P(m,am2+c),A(﹣t,0),B(t,0),则at2+c=0,c=﹣at2.
∵PQ∥OF,
∴,
∴OFamt+at2.
同理OE=﹣amt+at2.
∴OE+OF=2at2=﹣2c=2OC.
∴2.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练二次函数压轴题训练
1.如图,抛物线y=x2+bx+c过点A(﹣1,0)、点B(5,0),交y轴于点C.
(1)求b,c的值.
(2)点P(x0,y0)(0<x0<5)是抛物线上的动点.
①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;
②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
2.如图,二次函数的图象与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C,顶点为D.O为坐标原点,.
(1)求二次函数的表达式;
(2)求四边形ACDB的面积;
(3)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.
3.如图1,抛物线y=ax2+bx+c(a,b,c为常数)经过点F(0,5),
顶点坐标为(2,9),点P(x1,y1)为抛物线上的动点,PH⊥x轴于H,且.
(1)求抛物线的表达式;
(2)如图1,直线OP:交BF于点G,求的最大值;
(3)如图2,四边形OBMF为正方形,PA交y轴于点E,BC交FM的延长线于C,且BC⊥BE,PH=FC,求点P的横坐标.
4.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).
(1)若二次函数的图象经过点(0,4),对称轴为直线x=1,求此二次函数的表达式;
(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1,求实数m的最小值.
5.如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求b、c的值;
(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.
①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;
②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
6.在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
7.如图,抛物线y=mx2﹣16mx+48m(m>0)与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值;
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示);
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0,y0)总有n4my02﹣12y0﹣50成立,求实数n的最小值.
8.已知:y关于x的函数y=(a﹣2)x2+(a+1)x+b.
(1)若函数的图象与坐标轴有两个公共点,且a=4b,则a的值是 ;
(2)如图,若函数的图象为抛物线,与x轴有两个公共点A(﹣2,0),B(4,0),并与动直线l:x=m(0<m<4)交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为S1,△CDE的面积为S2.
①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,S1﹣S2是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
9.如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(﹣1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式;
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;
(3)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于两点A(﹣3,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)已知抛物线上有一点P(x0,y0),其中y0<0,若∠CAO+∠ABP=90°,求x0的值;
(3)若点D,E分别是线段AC,AB上的动点,且AE=2CD,求CE+2BD的最小值.
11.如图,抛物线yx2x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
12.已知抛物线y=ax2+bx+c过点A(﹣2,0),B(4,0),D(0,﹣8).
(1)求抛物线的解析式及顶点E的坐标;
(2)如图,抛物线y=ax2+bx+c向上平移,使顶点E落在x轴上的P点,此时的抛物线记为C,过P作两条互相垂直的直线与抛物线C交于不同于P的M,N两点(M位于N的右侧),过M,N分别作x轴的垂线交x轴于点M1,N1.
①求证:△PMM1∽△NPN1;
②设直线MN的方程为y=kx+m,求证:k+m为常数.
13.如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B,D(﹣4,5)两点,且与直线DC交于另一点E.
(1)求抛物线的解析式;
(2)F为抛物线对称轴上一点,Q为平面直角坐标系中的一点,是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由;
(3)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为M,连接ME,BP,探究EM+MP+PB是否存在最小值.若存在,请求出这个最小值及点M的坐标;若不存在,请说明理由.
14.如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,),与x轴交于A、B两点.
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.
(3)在(2)的条件下,点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.
(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
15.抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上一点,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案
1.【解答】解:(1)∵抛物线y=x2+bx+c过点A(﹣1,0)、点B(5,0),
∴抛物线的表达式为:y=(x+1)(x﹣5)=x2﹣4x﹣5,
∴b=﹣4,c=﹣5;
(2)由(1)得,抛物线的解析式为:y=x2﹣4x﹣5,
令x=0,则y=﹣5;
∴C(0,﹣5)
∴直线BC的表达式为:y=x﹣5,P(x0,4x0﹣5),
①如图,过点P作x轴的垂线,交线段BC于点D,
则D(x0,x0﹣5),
∴S△PBCOB PD5×(x0﹣54x0+5)
x0
(x0﹣2.5)2,
∴当x0=2.5时,S的值取最大,最大值为;
②存在,理由如下:
由题意可知,PE⊥PF,若△PEF是等腰直角三角形,则PE=PF,
由①可得,PE=x0﹣5﹣x02+4x0+55x0,
∵PF∥x轴,
∴F(4﹣x0,4x0﹣5),
∴PF=|2x0﹣4|,
∴|2x0﹣4|5x0,
解得x0=﹣1(舍)或x0=4或x0或x0(舍),
∴当△PEF是等腰直角三角形时,点P的坐标为(4,﹣5),(,).
2.【解答】解:(1)∵AO=1,tan∠ACO,
∴OC=5,即C的坐标为(0,5),
∵二次函数的图象与x轴交于A(﹣1,0),B(5,0)两点且过C的坐标(0,5),
设二次函数的解析式为y=ax2+bx+c,代入得:
,
解得:,
∴二次函数的解析式为y=﹣x2+4x+5;
(2)y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴顶点的坐标为(2,9),
过D作DN⊥AB于N,作DM⊥OC于M,
四边形ACDB的面积=S△AOC+S矩形OMDN﹣S△CDM+S△DNB
;
(3)如图,P是抛物线上的一点,且在第一象限,当∠ACO=∠PBC时,
连接PB,过C作CE⊥BC交BP于E,过E作EF⊥OC于F,
∵OC=OB=5,则BC=5,
∵∠ACO=∠PBC,
∴tan∠ACO=tan∠PBC,
即,
∴,
∵OC=OB,
∴∠OCB=45°,
∴∠ECF=180°﹣90°﹣45°=45°,
∴△EFC是等腰直角三角形,
∴FC=FE=1,
∴E的坐标为(1,6),
所以过B、E的直线的解析式为,
令,
解得,或,
所以BE直线与抛物线的两个交点为,
即所求P的坐标为.
3.【解答】解:(1)∵抛物线y=ax2+bx+c(a,b,c为常数)经过点F(0,5),顶点坐标为(2,9),
∴,
解得,
∴抛物线的表达式为y=﹣x2+4x+5;
(2)过点G作GT⊥x轴于点T,如图所示,
在y=﹣x2+4x+5中,令y=0得0=﹣x2+4x+5,
解得x=5或x=﹣1,
∴A(﹣1,0),B(5,0),
∵F(0,5),
∴BO=FO=5,
设直线BF的解析式为:y=kx+5,
∴y=5k+5,
解得k=﹣1,
∴直线BF的解析式为y=﹣x+5,
由G在直线BF上,设G(m,﹣m+5),
∵G在直线OP上,直线OP为,
∴﹣m+5m,
∴,
∴,
由P(x1,y1) 在抛物线 y=﹣x2+4x+5上,知P(x1,4x1+5),
∴,
∵S△BPG=S△BPO﹣S△BOG,
∴111,
∵,
∴111(x1)2,
∵,,
∴当 时,取最大值,最大值为;
(3)设MF交PH于T,如图:
∵OBFM为正方形,F(0,5),
∴FM=BM=OF=BO=5,∠MBO=90°,FC∥OB,
∵PH⊥x,∠MBO=90°,FC∥OB,
∴MTBH为矩形,
∴TH=MB=FM=5,
∵PH=FC,
∴PT=MC,
∵BC⊥BE,
∴∠MBC+∠MBE=90°,
∵∠MBO=90°,
∴∠OBE+∠MBE=90°,
∴∠OBE=∠MBC,
∴∠CMB=∠EOB=90°,
∴△EOB∽△CMB,
∴,
∵OB=MB,
∴EO=MC,
∵PH=FC,
∴PT=MC,
∴EO=MC=PT,
设 EO=MC=PT=a,
∴PH=PT+TH=5+a,E(0,a),
∵A(﹣1,0),
设直线AP的解析式为y=kx+b,
则,
∴,
∴直线AP的解析式为y=ax+a,
∵PH=a+5,P在直线AP上,
∴a+5=ax+a,
∴,即P点横坐标为 ,
∴x1,y1=a+5,
∴a,y15
∴54x1+5,
∴45=0,
∴(x1+1)(5x1+5)=0,
解得x1=1或x1或x1,
∵x1,
∴x1,
∴点P的横坐标为.
方法2:
设P(m,﹣m2+4m+5),
∴OH=m,PH=﹣m2+4m+5,
∵tan∠EAO,
∴,
∴EO=5﹣m,
∵BC⊥BE,
∴∠CBM=90°﹣∠MBE=∠EBO,
∵∠CMB=90°=∠EOB,BM=OB,
∴△CMB≌△EOB(ASA),
∴CM=EO=5﹣m,
∴CF=CM+FM=5﹣m+5=10﹣m,
∵PH=CF,
∴﹣m2+4m+5=10﹣m,
解得m或m,
∵m,
∴m,
∴点P的横坐标为.
4.【解答】解:(1)∵二次函数的图象经过点(0,4),
∴c=4;
∵对称轴为直线:x1,
∴b=﹣2,
∴此二次函数的表达式为:y1=x2﹣2x+4.
(2)当b2﹣c=0时,b2=c,此时函数的表达式为:y1=x2+bx+b2,
根据题意可知,需要分三种情况:
①当b,即b<0时,二次函数的最小值在x=b处取到;
∴b2+b2+b2=21,解得b1,b2(舍去);
②b﹣3,即b>2时,二次函数的最小值在x=b﹣3处取到;
∴(b﹣3)2+b(b﹣3)+b2=21,解得b3=4,b4=﹣1(舍去);
③b﹣3b,即0≤b≤2时,二次函数的最小值在x处取到;
∴()2+b ()+b2=21,解得b=±2(舍去).
综上所述,b的值为或4.
(3)由(1)知,二次函数的表达式为:y1=x2﹣2x+4,
设函数y3=y2﹣y1=x2+3x+m﹣4,
对称轴为直线x0,
∴当0≤x≤1时,y3随x的增大而增大,
∴当x=0时,y3即y2﹣y1有最小值m﹣4,
∴m﹣4≥0,
∴m≥4,即m的最小值为4.
5.【解答】解:(1)由二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),得:
,
解得:,
∴y=x2﹣2x﹣3,
∴b=﹣2,c=﹣3.
(2)①∵点P(m,n)在抛物线上y=x2﹣2x﹣3,
∴P(m,m2﹣2m﹣3),
∴PQ=m﹣(m2﹣2m﹣3)=﹣m2+3m+3=﹣(m)2,
∵过P作x轴的垂线交直线l:y=x于点Q,
∴Q(m,m),
设点P到直线y=x的距离为h,
∵直线y=x是一三象限的角平分线,
∴PQh,
∴当P点到直线l:y=x的距离最大时,PQ取得最大值,
∴当m时,PQ有最大值,
∴当P点到直线l:y=x的距离最大时,m的值为.
②∵抛物线与y轴交于点C,
∴x=0时,y=﹣3,
∴C(0,﹣3),
∵OC∥PQ,且以点O、C、P、Q为顶点的四边形是菱形,
∴PQ=OC,
又∵OC=3,PQ=|﹣m2+3m+3|,
∴3=|﹣m2+3m+3|,
解得:m1=0,m2=3,m3,m4,
当m1=0时,PQ与OC重合,菱形不成立,舍去;
当m2=3时,P(3,0),Q(3,3),
此时,四边形OCPQ是平行四边形,OQ,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m3时,Q(,),
此时,四边形OCQP是平行四边形,OQ,
∴CQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m4时,Q(,),
此时,四边形OCQP是平行四边形,OQ,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
综上所述:不存在m,使得以点O、C、P、Q为顶点的四边形是菱形.
6.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),
∴,
解得,,
∴抛物线的解析式为y2;
(2)①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由,可得,
∴x1+x2=2k,x1 x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②假设抛物线上存在点P(m,2),使得点P与点Q关于直线l对称,
∴OP=OQ,即,
解得,,,m3=1,m4=﹣1,
∵m3=1,m4=﹣1不合题意,舍去,
当时,点P(),
线段PQ的中点为(),
∴,
∴,
∴直线l的表达式为:y=(1)x,
当时,点P(,),
线段PQ的中点为(,﹣1),
∴,
∴,
∴直线l的解析式为y=(1)x.
综上,点P(,),直线l的解析式为y=(1)x或点P(,),直线l的解析式为y=(1)x.
7.【解答】解:(1)令y=mx2﹣16mx+48m=m(x﹣4)(x﹣12)=0,则x1=12,x2=4,
∴A(12,0),即OA=12,
又∵C(0,48m),
∴当△OAC为等腰直角三角形时,OA=OC,
即12=48m,
∴m;
(2)由(1)可知点C(0,48m),
∵对任意m>0,C、E两点总关于原点对称,
∴必有E(0,﹣48m),
设直线AE的解析式为y=kx+b,
将E(0,﹣48m),A(12,0)代入,可得
,解得,
∴直线AE的解析式为y=4mx﹣48m,
∵点D为直线AE与抛物线的交点,
∴解方程组,可得或(点A舍去),
即点D的坐标为(8,﹣16m);
(3)当∠ODB=∠OAD,∠DOB=∠AOD时,△ODB∽△OAD,
∴OD2=OA×OB=4×12=48,
∴OD=4,
又∵点D为线段AE的中点,
∴AE=2OD=8,
又∵OA=12,
∴OE4,
∴D(6,﹣2),
把D(6,﹣2)代入抛物线y=mx2﹣16mx+48m,可得﹣236m﹣96m+48m,
解得m,
∴抛物线的解析式为y(x﹣4)(x﹣12),
即y(x﹣8)2,
∵点P(x0,y0)为抛物线上任意一点,
∴y0,
令t=﹣4my02﹣12y0﹣50=﹣2y02﹣12y0﹣50=﹣2(y0+3)2+4,
则当y0时,t最大值=﹣2(3)2+4,
若要使n4my02﹣12y0﹣50成立,则n,
∴n≥3,
∴实数n的最小值为.
8.【解答】解:(1)①当a﹣2=0时,即a=2时,
y关于x的函数解析式为y=3x,
此时y=3x与x轴的交点坐标为(,0),
与y轴的交点坐标为(0,);
②当a﹣2≠0时,y关于x的函数为二次函数,
∵二次函数图象抛物线与坐标轴有两个交点,
∴抛物线可能存在与x轴有两个交点,其中一个交点为坐标原点或与x轴有一个交点与y轴一个交点两种情况.
当抛物线与x轴有两个交点且一个为坐标原点时,
由题意得b=0,此时a=0,抛物线为y=﹣2x2+x.
当y=0时,﹣2x2+x=0,
解得x1=0,x2.
∴其图象与x轴的交点坐标为(0,0)(,0).
当抛物线与x轴有一个交点与y轴有一个交点时,
由题意得,y=(a﹣2)x2+(a+1)x+b所对应的一元二次方程(a﹣2)x2+(a+1)x+b=0有两个相等实数根.
∴Δ=(a+1)2﹣4(a﹣2)a=0,
解得a,
此时yx2x,
当x=0时,y,
∴与y轴的交点坐标为(0,),
当y=0时,x2x0,
解得x1=x2,
∴与x轴的交点坐标为(,0),
综上所述,若y关于x的函数y=(a﹣2)x2+(a+1)x+b的图象与坐标轴有两个交点,则a可取的值为2,0,,
故答案为:2或0或;
(2)①如图,设直线l与BC交于点F,
根据题意得,
解得,
∴抛物线的解析式为y=﹣x2+2x+8,
当x=0时,y=8,
∴C(0,8),
∵y=﹣x2+2x+8=﹣(x﹣1)2+9,点P为抛物线顶点,
∴P(1,9),
∵B(4,0),C(0,8),
∴直线BC的解析式为y=﹣2x+8,
∴F(1,6),
∴PF=9﹣6=3,
∴△PBC的面积OB PF6;
②S1﹣S2存在最大值,
理由:如图,设直线x=m交x轴于H,
由①得,OB=4,AO=2,AB=6,OC=8,AH=2+m,P(m,﹣m2+2m+8),
∴PH=﹣m2+2m+8,
∵OD∥PH,
∴△AOD∽△AHP,
∴,
∴,
∴OD=8﹣2m,
∵S1﹣S2=S△PAB﹣S△AOD﹣S△OBC3m2+8m=﹣3(m)2,
∵﹣3<0,0<m<4,
∴当m时,S1﹣S2存在最大值,最大值为.
9.【解答】解:(1)∵抛物线y=ax2+bx+c过点A(﹣1,0),B(2,0),
∴抛物线的表达式为y=a(x+1)(x﹣2),
将点C(0,2)代入得,2=﹣2a,
∴a=﹣1,
∴抛物线的表达式为y=﹣(x+1)(x﹣2),即y=﹣x2+x+2.
设直线BC的表达式为y=kx+t,
将B(2,0),C(0,2)代入得,
,
解得,
∴直线BC的表达式为y=﹣x+2.
(2)∵点M在直线BC上,且P(m,n),
∴点M的坐标为(m,﹣m+2),
∴OC=2
∴CM2=(m﹣0)2+(﹣m+2﹣2)2=2m2,OM2=m2+(﹣m+2)2=2m2﹣4m+4,
当△OCM为等腰三角形时,
①若CM=OM,则CM2=OM2,
即2m2=2m2﹣4m+4,
解得m=1;
②若CM=OC,则CM2=OC2,
即2m2=4,
解得或m(舍去);
③若OM=OC,则OM2=OC2,
即2m2﹣4m+4=4,
解得m=2(舍)或m=0(舍去).
综上,m=1或m.
(3)∵点P与点C相对应,
∴△POQ∽△CBN或△POQ∽△CNB,
①若点P在点B的左侧,
则,
当△POQ∽△CBN,即∠POQ=45°时,
直线OP的表达式为y=x,
∴﹣m2+m+2=m,
解得或m(舍去),
∴,即OP=2,
∴,即,
解得OQ,
∴,
当△POQ∽△CNB,即∠PQO=45°时,
,
∴,即,
解得m=1±(舍去).
当△POQ∽△CNB,即∠PQO=45°时,
PQ,OQ=m﹣(﹣m2+m+2)=m2﹣2,
∴,即,
解得m,(负值舍去),
∴P(),Q(0.).
②若点P在点B的右侧,
则∠CBN=135°,BN=m﹣2,
当△POQ∽△CBN,即∠POQ=135°时,
直线OP的表达式为y=﹣x,
∴﹣m2+m+2=﹣m,
解得m=1或m=1(舍去),
∴,
∴,即,
解得OQ=1,
∴,
当△POQ∽△CNB,即∠PQO=135°时,
PQ,OQ=m2﹣2m﹣2,
∴,即,
解得m=1(舍)或m=1(舍去),
综上,P(),Q(0, )或P(),Q(0.)或P(),Q(0,)或.
10.【解答】解:(1)设抛物线的表达式为:y=a(x+3)(x﹣4)=a(x2﹣x﹣12),
即﹣12a=4,则a,
故抛物线的表达式为:yx2x+4①;
(2)在Rt△AOC中,tan∠CAO,
∵∠CAO+∠ABP=90°,
则tan∠ABP,
故设直线BP的表达式为:y(x﹣4)②,
联立①②得:x2x+4(x﹣4),
解得:xx0(不合题意的值已舍去);
(3)作∠EAG=∠BCD,
设AG=2BC=2×48,
∵AE=2CD,
∴△BCD∽△GAE且相似比为1:2,
则EG=2BD,
故当C、E、G共线时,CE+2BD=CE+EG=CG为最小,
在△ABC中,设AC边上的高为h,
则S△ABCAC hAB×CO,
即5h=4×7,
解得:h,
则sin∠ACBsin∠EAG,
则tan∠EAG=7,
过点G作GN⊥x轴于点N,
则NG=AG sin∠EAG,
即点G的纵坐标为:,
同理可得,点G的横坐标为:,
即点G(,),
由点C、G的坐标得,CG,
即CE+2BD的最小值为.
11.【解答】解:(1)令x=0,则y=4,
∴C(0,4);
令y=0,则x2x+4=0,
∴x=﹣2或x=3,
∴A(﹣2,0),B(3,0).
故答案为:(﹣2,0);(3,0);(0,4).
(2)①∵CP∥x轴,C(0,4),
∴P(1,4),
∴CP=1,AB=5,
∵CP∥x轴,
∴.
②如图,过点P作PQ∥AB交BC于点Q,
∴直线BC的解析式为:yx+4.
设点P的横坐标为m,
则P(m,m2m+4),Q(m2m,m2m+4).
∴PQ=m﹣(m2m)m2m,
∵PQ∥AB,
∴(m)2,
∴当m时,的最大值为.
另解:分别过点P,A作y轴的平行线,交直线BC于两点,仿照以上解法即可求解.
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.
过点C作CF∥x轴交抛物线于点F,
∵∠BCO+2∠PCB=90°,∠BCO+∠BCM+∠MCF=90°,
∴∠MCF=∠BCP,
延长CP交x轴于点M,
∵CF∥x轴,
∴∠PCF=∠BMC,
∴∠BCP=∠BMC,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,
∴M(8,0),
∴直线CM的解析式为:yx+4,
令x2x+4x+4,
解得x或x=0(舍),
∴存在点P满足题意,此时m.
12.【解答】(1)解:将A(﹣2,0),B(4,0),D(0,﹣8)代入y=ax2+bx+c,
∴,
解得,
∴y=x2﹣2x﹣8,
∵y=x2﹣2x﹣8=(x﹣1)2﹣9,
∴E(1,﹣9);
(2)①证明:∵PN⊥PM,
∴∠MPN=90°,
∴∠NPN1+∠MPM1=90°,
∵NN1⊥x轴,MM1⊥x轴,
∴∠NN1P=∠MM1P=90°,
∴∠N1PN+∠PNN1=90°,
∴∠MPM1=∠PNN1,
∴△PMM1∽△NPN1;
②证明:由题意可知平移后的抛物线解析式为y=(x﹣1)2,
设N(x1,kx1+m),M(x2,kx2+m),
联立方程组,
整理得x2﹣(2+k)x+1﹣m=0,
∴x1+x2=2+k,x1 x2=1﹣m,
∵△PMM1∽△NPN1,
∴,即,
∴k+m=(k+m)2,
∴k+m=1或k+m=0,
∵M、N与P不重合,
∴k+m=1,
∴k+m为常数.
13.【解答】解:(1)由点D的纵坐标知,正方形ABCD的边长为5,
则OB=AB﹣AO=5﹣4=1,故点B的坐标为(1,0),
则,解得,
故抛物线的表达式为y=x2+2x﹣3;
(2)存在,理由:
∵点D、E关于抛物线对称轴对称,故点E的坐标为(2,5),
由抛物线的表达式知,其对称轴为直线x=﹣1,故设点F的坐标为(﹣1,m),
由点B、E的坐标得,BE2=(2﹣1)2+(5﹣0)2=26,
设点Q的坐标为(s,t),
∵以点Q,F,E,B为顶点的四边形是以BE为边的菱形,
故点B向右平移1个单位向上平移5个单位得到点E,则Q(F)向右平移1个单位向上平移5个单位得到点F(Q),且BE=EF(BE=EQ),
则或,
解得或,
故点F的坐标为(﹣1,5)或(﹣1,5)或(﹣1,)或(﹣1,);
(3)存在,理由:
由题意抛物线的对称轴交x轴于点B′(﹣1,0),将点B′向左平移1个单位得到点B″(﹣2,0),
连接B″E,交函数的对称轴于点M,过点M作MP⊥y轴,则点P、M为所求点,此时EM+MP+PB为最小,
理由:∵B′B″=PM=1,且B′B″∥PM,故四边形B″B′PM为平行四边形,则B″M=B′P=BP,
则EM+MP+PB=EM+1+MB″=B″E+1为最小,
由点B″、E的坐标得,直线B″E的表达式为y(x+2),
当x=﹣1时,y(x+2),故点M的坐标为(﹣1,),
则EM+MP+PB的最小值B″E+1=11.
14.【解答】解:(1)由题可列方程组:,解得:
∴抛物线解析式为:yx2x﹣2;
(2)如图1,令y=0,可得x2x﹣2=0,
解得x=﹣1或3,
∴A(﹣1,0).B(3,0),C(0,﹣2),
∴AB=4,
∠AOC=90°,AC,AB=4,
设直线AC的解析式为:y=kx+b,则,解得:,
∴直线AC的解析式为:y=﹣2x﹣2;
当△AOC∽△AEB时
()2=()2,
∵S△AOC=1,∴S△AEB,
∴AB×|yE|,AB=4,则yE,
则点E(,);
由△AOC∽△AEB得:
∴;
(3)如图2,连接BF,过点F作FG⊥AC于G,
则FG=CFsin∠FCGCF,
∴CF+BF=GF+BF≥BE,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO
∴BE=ABcos∠ABE=ABcos∠ACO=4,
|y|=OBtan∠ABE=OBtan∠ACO=3,
∴当y时,即点F(0,),CF+BF有最小值为;
(4)①当点Q为直角顶点时(如图3):
由(3)易得F(0,),
∵C(0,﹣2)∴H(0,2)
设Q(1,m),过点Q作QM⊥y轴于点M.
则Rt△QHM∽Rt△FQM
∴QM2=HM FM,
∴12=(2﹣m)(m),
解得:m,
则点Q(1,)或(1,)
②当点H为直角顶点时:
点H(0,2),则点Q(1,2);
③当点F为直角顶点时:
同理可得:点Q(1,);
综上,点Q的坐标为:(1,)或(1,)或Q(1,2)或Q(1,).
15.【解答】解:(1)①将P(1,﹣3),B(4,0)代入y=ax2+c,得
,解得,
抛物线的解析式为yx2;
②如图1,
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为yx
解方程组得,.
∵P(1,﹣3),
∴D(,).
∴点D的坐标为(﹣1,﹣3)或(,).
(2)点P运动时,是定值,定值为2,理由如下:
作PQ⊥AB于Q点,设P(m,am2+c),A(﹣t,0),B(t,0),则at2+c=0,c=﹣at2.
∵PQ∥OF,
∴,
∴OFamt+at2.
同理OE=﹣amt+at2.
∴OE+OF=2at2=﹣2c=2OC.
∴2.
21世纪教育网(www.21cnjy.com)
同课章节目录
