2025年中考数学一轮复习 9 平面直角坐标系与函数基础 小测验(含详解)
文档属性
| 名称 | 2025年中考数学一轮复习 9 平面直角坐标系与函数基础 小测验(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 17:55:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9 平面直角坐标系与函数基础
分值:50分 时间30分钟
选择题(15分)
1、(2024·四川广元·中考真题)如果单项式与单项式的和仍是一个单项式,则在平面直角坐标系中点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、(2024·辽宁大连·三模)在化学学习中,我们在研究某物质的性质时,常常会用到“价类二维图”来研究该物质化合价的变化问题.如下图所示为硫元素化合价的“价类二维图”,则在A、B、E、H四种物质中,硫元素化合价最低的为( )
A.A B.B C.E D.H
3、(2024·山西·模拟预测)某树苗的初始高度为,如图,这是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则该树苗的高度与生长月数之间的函数关系式为( )
B.
C. D.
4、(2024·陕西西安·模拟预测)正比例函数图象上一点P到x轴的距离与y轴距离之比为2,且y的值随x值的增大而减小,则k的值为( )
A. B.2 C. D.
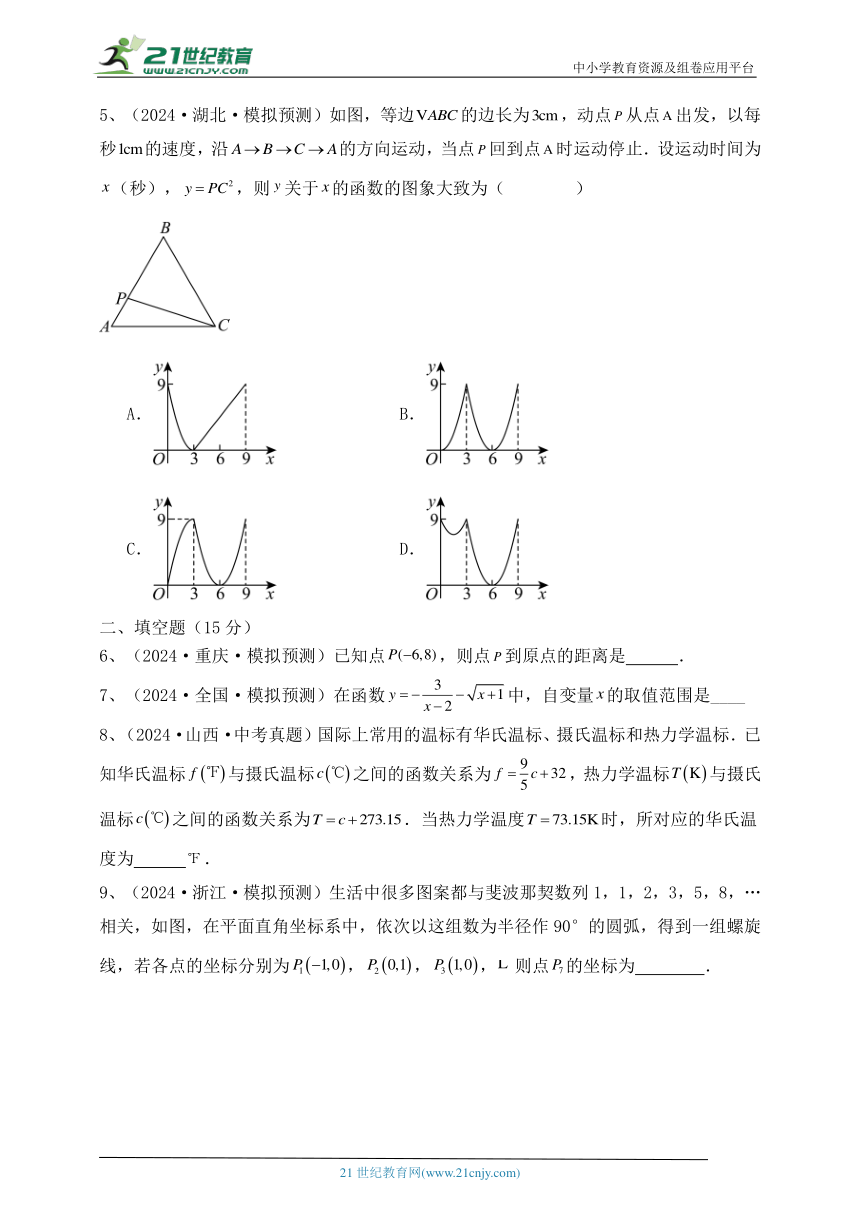
5、(2024·湖北·模拟预测)如图,等边的边长为,动点从点出发,以每秒的速度,沿的方向运动,当点回到点时运动停止.设运动时间为(秒),,则关于的函数的图象大致为( )
A. B.
C. D.
填空题(15分)
6、(2024·重庆·模拟预测)已知点,则点到原点的距离是 .
7、(2024·全国·模拟预测)在函数中,自变量的取值范围是____
8、(2024·山西·中考真题)国际上常用的温标有华氏温标、摄氏温标和热力学温标.已知华氏温标与摄氏温标之间的函数关系为,热力学温标与摄氏温标之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
9、(2024·浙江·模拟预测)生活中很多图案都与斐波那契数列1,1,2,3,5,8,…相关,如图,在平面直角坐标系中,依次以这组数为半径作90°的圆弧,得到一组螺旋线,若各点的坐标分别为,,,则点的坐标为 .
10、(2024·河南·中考真题)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
解答题(20分)
11、(2024·河北·模拟预测)某班级同学从学校出发去白鹿原研学旅行,一部分坐大客车先出发,余下的几人后乘坐小轿车沿同一路线出行,大客车中途停车等候,后小轿车赶了上来,大客车随即开动,以出发时速度的继续行驶,小轿车保持原速度不变,最终两车相继到达了景点入口,两车距学校的路程单位:和行驶时间单位:之间的函数关系如图所示,请结合图象解决下列问题.
(1)求大客车在途中等候时距学校的路程有多远?
(2)在小轿车到达景点入口时,大客车离景点入口还有多远?
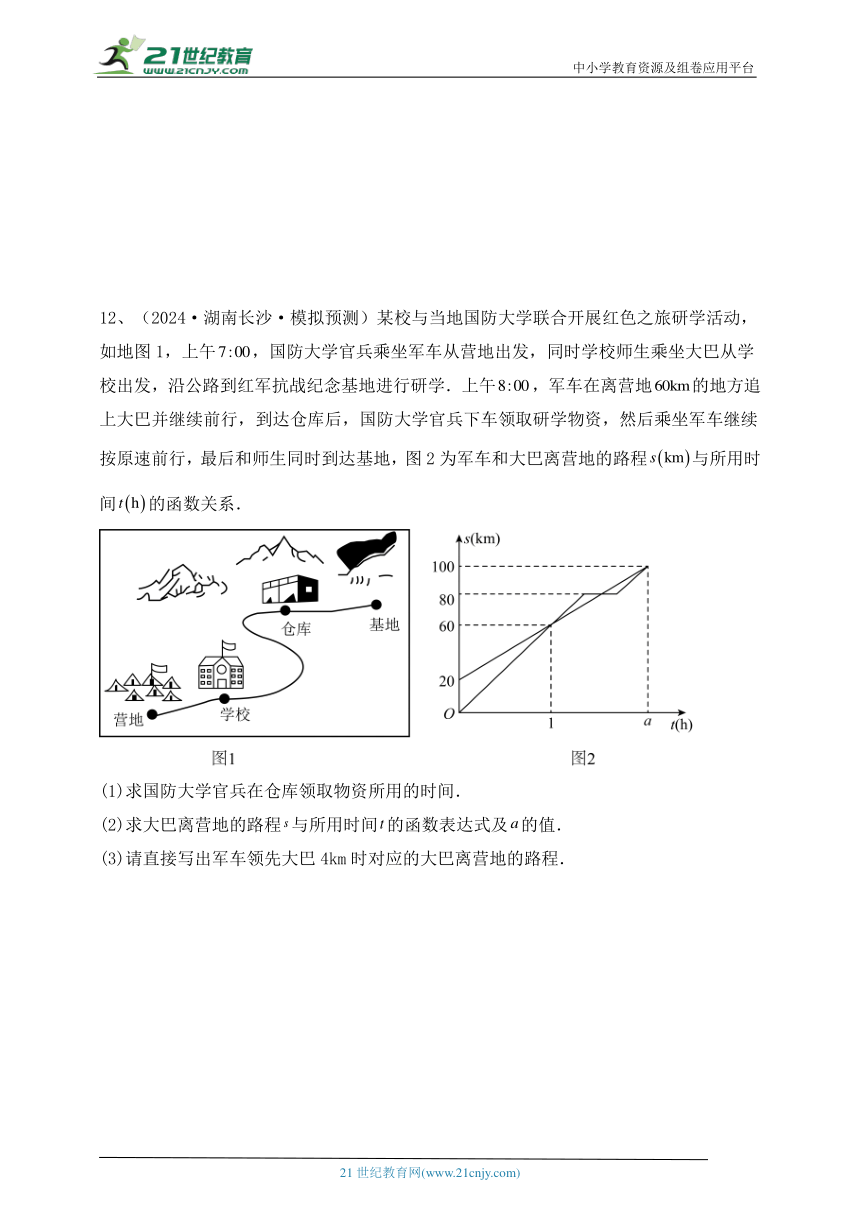
12、(2024·湖南长沙·模拟预测)某校与当地国防大学联合开展红色之旅研学活动,如地图1,上午,国防大学官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路到红军抗战纪念基地进行研学.上午,军车在离营地的地方追上大巴并继续前行,到达仓库后,国防大学官兵下车领取研学物资,然后乘坐军车继续按原速前行,最后和师生同时到达基地,图2为军车和大巴离营地的路程与所用时间的函数关系.
(1)求国防大学官兵在仓库领取物资所用的时间.
(2)求大巴离营地的路程与所用时间的函数表达式及的值.
(3)请直接写出军车领先大巴4km时对应的大巴离营地的路程.
13、(2024·重庆·模拟预测)如图,四边形是边长为的菱形,,动点分别以每秒个单位长度的速度同时从点出发,点沿折线方向运动,点沿折线方向运动,当两点相遇时停止运动.设运动时间为秒,点两点间的距离为.
(1)请直接写出关于的函数表达式并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出点相距个单位长度时的值.(结果保留一位小数)
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
答案:
一、选择题(15分)
1、(2024·四川广元·中考真题)如果单项式与单项式的和仍是一个单项式,则在平面直角坐标系中点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【详解】解:∵单项式与单项式的和仍是一个单项式,
∴单项式与单项式是同类项,
∴,
解得,,
∴点在第四象限,
故选:D
2、(2024·辽宁大连·三模)在化学学习中,我们在研究某物质的性质时,常常会用到“价类二维图”来研究该物质化合价的变化问题.如下图所示为硫元素化合价的“价类二维图”,则在A、B、E、H四种物质中,硫元素化合价最低的为( )
A.A B.B C.E D.H
【答案】A
3、(2024·山西·模拟预测)某树苗的初始高度为,如图,这是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则该树苗的高度与生长月数之间的函数关系式为( )
A. B. C. D.
【答案】D
【详解】解:由题意得,树苗每个月增长的高度是,
故该树苗的高度与生长月数之间的函数关系式为,
故选:.
4、(2024·陕西西安·模拟预测)正比例函数图象上一点P到x轴的距离与y轴距离之比为2,且y的值随x值的增大而减小,则k的值为( )
A. B.2 C. D.
【答案】A
【详解】解;设,
∵点P到x轴的距离与y轴距离之比为2,
∴,
∴,
∵y的值随x值的增大而减小,
∴,
∴,
故选:A.
5、(2024·湖北·模拟预测)如图,等边的边长为,动点从点出发,以每秒的速度,沿的方向运动,当点回到点时运动停止.设运动时间为(秒),,则关于的函数的图象大致为( )
A. B.
C. D.
【答案】D
【详解】解:如图,过作于点,
则,,
①当点在上时,,,,
,
该函数图象是开口向上的抛物线,对称轴为直线;
由此可排除A,B,C.
②当时,即点在线段上时,;
则,
该函数的图象是在上的抛物线,且对称轴为;
③当时,即点在线段上,此时,,
则,
该函数的图象是在上的抛物线,且对称轴为直线;
二、填空题(15分)
6、(2024·重庆·模拟预测)已知点,则点到原点的距离是 .
【答案】
【详解】解:∵点P坐标为,
∴P到原点的距离为,
故答案:.
7、(2024·全国·模拟预测)在函数中,自变量的取值范围是____
【答案】且
8、(2024·山西·中考真题)国际上常用的温标有华氏温标、摄氏温标和热力学温标.已知华氏温标与摄氏温标之间的函数关系为,热力学温标与摄氏温标之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
【答案】
【详解】解:∵,
∴,
解得:,
∴
故答案为:.
9、(2024·浙江·模拟预测)生活中很多图案都与斐波那契数列1,1,2,3,5,8,…相关,如图,在平面直角坐标系中,依次以这组数为半径作90°的圆弧,得到一组螺旋线,若各点的坐标分别为,,,则点的坐标为 .
【答案】
【详解】解:观察发现:先向右平移1个单位,再向上平移1个单位得到;先向右平移1个单位,再向下平移1个单位得到;
先向左平移2个单位,再向下平移2个单位得到;
先向左平移3个单位,再向上平移3个单位得到;
先向右平移5个单位,再向上平移5个单位得到;
根据1,1,2,3,5,8,13,…的变化规律可知,
先向右平移8个单位,再向下平移8个单位得到;
故答案为
10、(2024·河南·中考真题)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
【答案】
【详解】解∶设正方形的边长为a,与y轴相交于G,
则四边形是矩形,
∴,,,
∵折叠,
∴,,
∵点A的坐标为,点F的坐标为,
∴,,
∴,
在中,,
∴,
解得,
∴,,
在中,,
∴,
解得,
∴,
∴点E的坐标为,
故答案为:.
三、简单题(20分)
11、(2024·河北·模拟预测)某班级同学从学校出发去白鹿原研学旅行,一部分坐大客车先出发,余下的几人后乘坐小轿车沿同一路线出行,大客车中途停车等候,后小轿车赶了上来,大客车随即开动,以出发时速度的继续行驶,小轿车保持原速度不变,最终两车相继到达了景点入口,两车距学校的路程单位:和行驶时间单位:之间的函数关系如图所示,请结合图象解决下列问题.
(1)求大客车在途中等候时距学校的路程有多远?
(2)在小轿车到达景点入口时,大客车离景点入口还有多远?
【答案】(1)
(2)
【详解】(1)解:由图象可得,
小轿车的速度为:,
,
即大客车在途中等候时距学校的路程有;
(2)解:大客车开始的速度为:,
大客车后来的速度为:,
,
即在小轿车到达景点入口时,大客车离景点入口还有.
12、(2024·湖南长沙·模拟预测)某校与当地国防大学联合开展红色之旅研学活动,如地图1,上午,国防大学官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路到红军抗战纪念基地进行研学.上午,军车在离营地的地方追上大巴并继续前行,到达仓库后,国防大学官兵下车领取研学物资,然后乘坐军车继续按原速前行,最后和师生同时到达基地,图2为军车和大巴离营地的路程与所用时间的函数关系.
(1)求国防大学官兵在仓库领取物资所用的时间.
(2)求大巴离营地的路程与所用时间的函数表达式及的值.
(3)请直接写出军车领先大巴4km时对应的大巴离营地的路程.
【答案】(1)
(2),
(3)或
【详解】(1)解:由图象可知,军车的速度为:,大巴车的速度为:,
∴军车到达仓库所用时间为:,
从仓库到达基地所用时间为:,
大巴车到达基地的时间为:,
∴部队官兵在仓库领取物资所用的时间为.
(2)解:由(1)知:大巴车的速度为:,大巴车到达基地的时间为:,
∴,;
(3)解:①当军车到达仓库之前:,
解得:,
把代入,得:;
13、(2024·重庆·模拟预测)如图,四边形是边长为的菱形,,动点分别以每秒个单位长度的速度同时从点出发,点沿折线方向运动,点沿折线方向运动,当两点相遇时停止运动.设运动时间为秒,点两点间的距离为.
(1)请直接写出关于的函数表达式并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出点相距个单位长度时的值.(结果保留一位小数)
【答案】(1)
(2)图象见解析,当时,随着的增大而增大,当时,随着的增大而减小
(3)秒或秒
【详解】(1)解:∵四边形是菱形,
∴,,
由题意知,当时, 在上运动,如图1,且是等边三角形,
图1
∴;
当时, 在上运动,如图2,且是等边三角形,
图2
∴;
综上所述,;
(2)解:函数图象如下;
由图象可得,当时,随着的增大而增大,当时,随着的增大而减小;
(3)解:当时,或,
解得,或,
∴点相距个单位长度时的值为秒或秒.
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
【答案】(1)1.0
(2)见详解
(3)1.2,8.5
【详解】(1)解:由题意得,设V与的函数关系式为:,
由表格数据得:,
解得:,
∴,
∴当时,,
∴;
(2)解:如图所示,即为所画图像,
(3)解:①当时,,由图象可知高度差,
故答案为:1.2;
②由图象可知当两个水杯的水面高度相同时,估算高度约为,
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
【答案】(1)1.0
(2)见详解
(3)1.2,8.5
【详解】(1)解:由题意得,设V与的函数关系式为:,
由表格数据得:,
解得:,
∴,
∴当时,,
∴;
(2)解:如图所示,即为所画图像,
(3)解:①当时,,由图象可知高度差,
故答案为:1.2;
②由图象可知当两个水杯的水面高度相同时,估算高度约为,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9 平面直角坐标系与函数基础
分值:50分 时间30分钟
选择题(15分)
1、(2024·四川广元·中考真题)如果单项式与单项式的和仍是一个单项式,则在平面直角坐标系中点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、(2024·辽宁大连·三模)在化学学习中,我们在研究某物质的性质时,常常会用到“价类二维图”来研究该物质化合价的变化问题.如下图所示为硫元素化合价的“价类二维图”,则在A、B、E、H四种物质中,硫元素化合价最低的为( )
A.A B.B C.E D.H
3、(2024·山西·模拟预测)某树苗的初始高度为,如图,这是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则该树苗的高度与生长月数之间的函数关系式为( )
B.
C. D.
4、(2024·陕西西安·模拟预测)正比例函数图象上一点P到x轴的距离与y轴距离之比为2,且y的值随x值的增大而减小,则k的值为( )
A. B.2 C. D.
5、(2024·湖北·模拟预测)如图,等边的边长为,动点从点出发,以每秒的速度,沿的方向运动,当点回到点时运动停止.设运动时间为(秒),,则关于的函数的图象大致为( )
A. B.
C. D.
填空题(15分)
6、(2024·重庆·模拟预测)已知点,则点到原点的距离是 .
7、(2024·全国·模拟预测)在函数中,自变量的取值范围是____
8、(2024·山西·中考真题)国际上常用的温标有华氏温标、摄氏温标和热力学温标.已知华氏温标与摄氏温标之间的函数关系为,热力学温标与摄氏温标之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
9、(2024·浙江·模拟预测)生活中很多图案都与斐波那契数列1,1,2,3,5,8,…相关,如图,在平面直角坐标系中,依次以这组数为半径作90°的圆弧,得到一组螺旋线,若各点的坐标分别为,,,则点的坐标为 .
10、(2024·河南·中考真题)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
解答题(20分)
11、(2024·河北·模拟预测)某班级同学从学校出发去白鹿原研学旅行,一部分坐大客车先出发,余下的几人后乘坐小轿车沿同一路线出行,大客车中途停车等候,后小轿车赶了上来,大客车随即开动,以出发时速度的继续行驶,小轿车保持原速度不变,最终两车相继到达了景点入口,两车距学校的路程单位:和行驶时间单位:之间的函数关系如图所示,请结合图象解决下列问题.
(1)求大客车在途中等候时距学校的路程有多远?
(2)在小轿车到达景点入口时,大客车离景点入口还有多远?
12、(2024·湖南长沙·模拟预测)某校与当地国防大学联合开展红色之旅研学活动,如地图1,上午,国防大学官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路到红军抗战纪念基地进行研学.上午,军车在离营地的地方追上大巴并继续前行,到达仓库后,国防大学官兵下车领取研学物资,然后乘坐军车继续按原速前行,最后和师生同时到达基地,图2为军车和大巴离营地的路程与所用时间的函数关系.
(1)求国防大学官兵在仓库领取物资所用的时间.
(2)求大巴离营地的路程与所用时间的函数表达式及的值.
(3)请直接写出军车领先大巴4km时对应的大巴离营地的路程.
13、(2024·重庆·模拟预测)如图,四边形是边长为的菱形,,动点分别以每秒个单位长度的速度同时从点出发,点沿折线方向运动,点沿折线方向运动,当两点相遇时停止运动.设运动时间为秒,点两点间的距离为.
(1)请直接写出关于的函数表达式并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出点相距个单位长度时的值.(结果保留一位小数)
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
答案:
一、选择题(15分)
1、(2024·四川广元·中考真题)如果单项式与单项式的和仍是一个单项式,则在平面直角坐标系中点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【详解】解:∵单项式与单项式的和仍是一个单项式,
∴单项式与单项式是同类项,
∴,
解得,,
∴点在第四象限,
故选:D
2、(2024·辽宁大连·三模)在化学学习中,我们在研究某物质的性质时,常常会用到“价类二维图”来研究该物质化合价的变化问题.如下图所示为硫元素化合价的“价类二维图”,则在A、B、E、H四种物质中,硫元素化合价最低的为( )
A.A B.B C.E D.H
【答案】A
3、(2024·山西·模拟预测)某树苗的初始高度为,如图,这是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则该树苗的高度与生长月数之间的函数关系式为( )
A. B. C. D.
【答案】D
【详解】解:由题意得,树苗每个月增长的高度是,
故该树苗的高度与生长月数之间的函数关系式为,
故选:.
4、(2024·陕西西安·模拟预测)正比例函数图象上一点P到x轴的距离与y轴距离之比为2,且y的值随x值的增大而减小,则k的值为( )
A. B.2 C. D.
【答案】A
【详解】解;设,
∵点P到x轴的距离与y轴距离之比为2,
∴,
∴,
∵y的值随x值的增大而减小,
∴,
∴,
故选:A.
5、(2024·湖北·模拟预测)如图,等边的边长为,动点从点出发,以每秒的速度,沿的方向运动,当点回到点时运动停止.设运动时间为(秒),,则关于的函数的图象大致为( )
A. B.
C. D.
【答案】D
【详解】解:如图,过作于点,
则,,
①当点在上时,,,,
,
该函数图象是开口向上的抛物线,对称轴为直线;
由此可排除A,B,C.
②当时,即点在线段上时,;
则,
该函数的图象是在上的抛物线,且对称轴为;
③当时,即点在线段上,此时,,
则,
该函数的图象是在上的抛物线,且对称轴为直线;
二、填空题(15分)
6、(2024·重庆·模拟预测)已知点,则点到原点的距离是 .
【答案】
【详解】解:∵点P坐标为,
∴P到原点的距离为,
故答案:.
7、(2024·全国·模拟预测)在函数中,自变量的取值范围是____
【答案】且
8、(2024·山西·中考真题)国际上常用的温标有华氏温标、摄氏温标和热力学温标.已知华氏温标与摄氏温标之间的函数关系为,热力学温标与摄氏温标之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
【答案】
【详解】解:∵,
∴,
解得:,
∴
故答案为:.
9、(2024·浙江·模拟预测)生活中很多图案都与斐波那契数列1,1,2,3,5,8,…相关,如图,在平面直角坐标系中,依次以这组数为半径作90°的圆弧,得到一组螺旋线,若各点的坐标分别为,,,则点的坐标为 .
【答案】
【详解】解:观察发现:先向右平移1个单位,再向上平移1个单位得到;先向右平移1个单位,再向下平移1个单位得到;
先向左平移2个单位,再向下平移2个单位得到;
先向左平移3个单位,再向上平移3个单位得到;
先向右平移5个单位,再向上平移5个单位得到;
根据1,1,2,3,5,8,13,…的变化规律可知,
先向右平移8个单位,再向下平移8个单位得到;
故答案为
10、(2024·河南·中考真题)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
【答案】
【详解】解∶设正方形的边长为a,与y轴相交于G,
则四边形是矩形,
∴,,,
∵折叠,
∴,,
∵点A的坐标为,点F的坐标为,
∴,,
∴,
在中,,
∴,
解得,
∴,,
在中,,
∴,
解得,
∴,
∴点E的坐标为,
故答案为:.
三、简单题(20分)
11、(2024·河北·模拟预测)某班级同学从学校出发去白鹿原研学旅行,一部分坐大客车先出发,余下的几人后乘坐小轿车沿同一路线出行,大客车中途停车等候,后小轿车赶了上来,大客车随即开动,以出发时速度的继续行驶,小轿车保持原速度不变,最终两车相继到达了景点入口,两车距学校的路程单位:和行驶时间单位:之间的函数关系如图所示,请结合图象解决下列问题.
(1)求大客车在途中等候时距学校的路程有多远?
(2)在小轿车到达景点入口时,大客车离景点入口还有多远?
【答案】(1)
(2)
【详解】(1)解:由图象可得,
小轿车的速度为:,
,
即大客车在途中等候时距学校的路程有;
(2)解:大客车开始的速度为:,
大客车后来的速度为:,
,
即在小轿车到达景点入口时,大客车离景点入口还有.
12、(2024·湖南长沙·模拟预测)某校与当地国防大学联合开展红色之旅研学活动,如地图1,上午,国防大学官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路到红军抗战纪念基地进行研学.上午,军车在离营地的地方追上大巴并继续前行,到达仓库后,国防大学官兵下车领取研学物资,然后乘坐军车继续按原速前行,最后和师生同时到达基地,图2为军车和大巴离营地的路程与所用时间的函数关系.
(1)求国防大学官兵在仓库领取物资所用的时间.
(2)求大巴离营地的路程与所用时间的函数表达式及的值.
(3)请直接写出军车领先大巴4km时对应的大巴离营地的路程.
【答案】(1)
(2),
(3)或
【详解】(1)解:由图象可知,军车的速度为:,大巴车的速度为:,
∴军车到达仓库所用时间为:,
从仓库到达基地所用时间为:,
大巴车到达基地的时间为:,
∴部队官兵在仓库领取物资所用的时间为.
(2)解:由(1)知:大巴车的速度为:,大巴车到达基地的时间为:,
∴,;
(3)解:①当军车到达仓库之前:,
解得:,
把代入,得:;
13、(2024·重庆·模拟预测)如图,四边形是边长为的菱形,,动点分别以每秒个单位长度的速度同时从点出发,点沿折线方向运动,点沿折线方向运动,当两点相遇时停止运动.设运动时间为秒,点两点间的距离为.
(1)请直接写出关于的函数表达式并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出点相距个单位长度时的值.(结果保留一位小数)
【答案】(1)
(2)图象见解析,当时,随着的增大而增大,当时,随着的增大而减小
(3)秒或秒
【详解】(1)解:∵四边形是菱形,
∴,,
由题意知,当时, 在上运动,如图1,且是等边三角形,
图1
∴;
当时, 在上运动,如图2,且是等边三角形,
图2
∴;
综上所述,;
(2)解:函数图象如下;
由图象可得,当时,随着的增大而增大,当时,随着的增大而减小;
(3)解:当时,或,
解得,或,
∴点相距个单位长度时的值为秒或秒.
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
【答案】(1)1.0
(2)见详解
(3)1.2,8.5
【详解】(1)解:由题意得,设V与的函数关系式为:,
由表格数据得:,
解得:,
∴,
∴当时,,
∴;
(2)解:如图所示,即为所画图像,
(3)解:①当时,,由图象可知高度差,
故答案为:1.2;
②由图象可知当两个水杯的水面高度相同时,估算高度约为,
14、(2024·北京·中考真题)小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,
当1号杯和2号杯中都有mL水时,小云分别记录了1号杯的水面高度(单位:cm)和2号杯的水面高度(单位:cm),部分数据如下:
/mL 0 40 100 200 300 400 500
/cm 0 2.5 5.0 7.5 10.0 12.5
/cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画与,与之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
【答案】(1)1.0
(2)见详解
(3)1.2,8.5
【详解】(1)解:由题意得,设V与的函数关系式为:,
由表格数据得:,
解得:,
∴,
∴当时,,
∴;
(2)解:如图所示,即为所画图像,
(3)解:①当时,,由图象可知高度差,
故答案为:1.2;
②由图象可知当两个水杯的水面高度相同时,估算高度约为,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
