第3章 图形的平移与旋转 能力提升测试题(含答案)
文档属性
| 名称 | 第3章 图形的平移与旋转 能力提升测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 18:58:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3章 图形的平移与旋转 能力提升测试题
考试范围:第3章 图形的平移与旋转;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
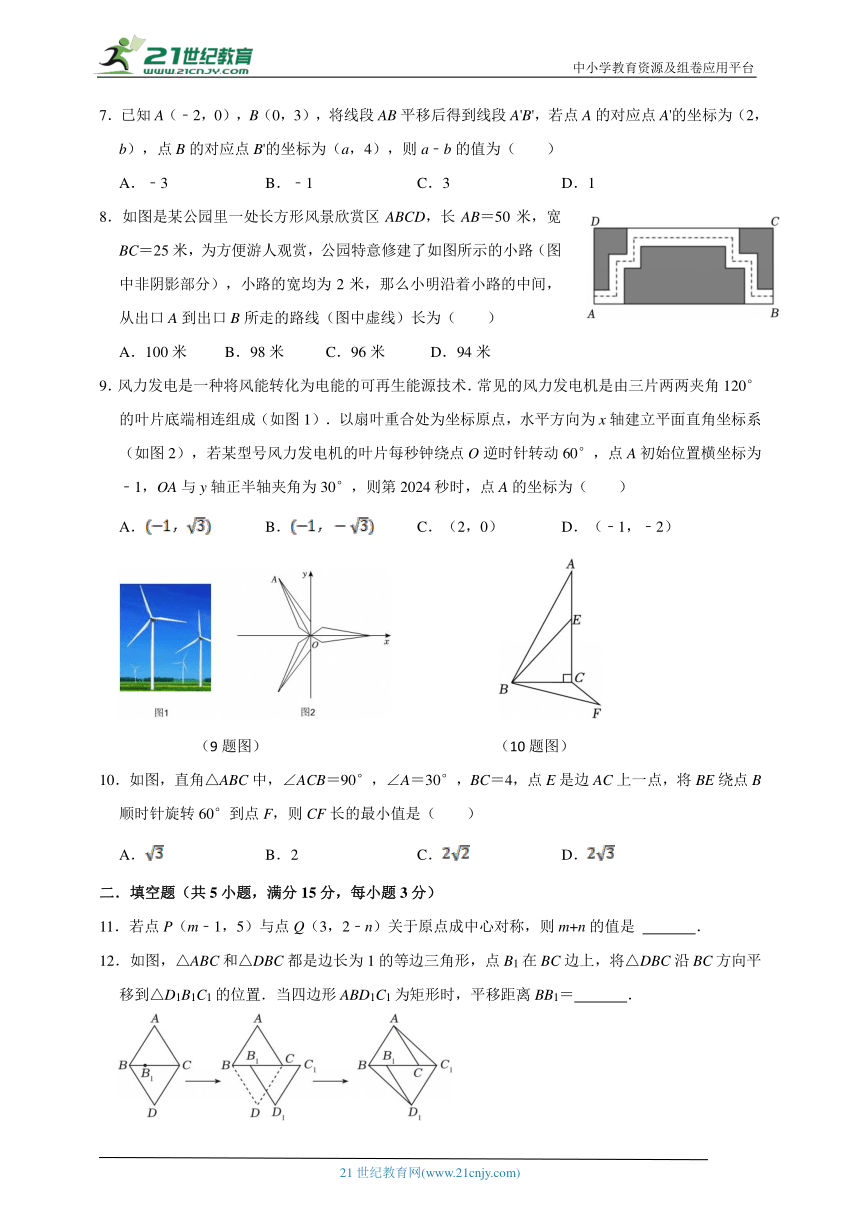
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )
A.2 B.2.5 C.3 D.5
3.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
(2题图) (3题图) (4题图) (5题图)
4.如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
A.60° B.105° C.120° D.135°
5.如图,将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,若CD=3,BC=1,则AD的长为( )
A. B. C.2 D.
6.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把其中一张扑克牌旋转180°.魔术师解除蒙具后,看到4张牌如图②所示.被旋转过的牌是( )
A.方块4 B.黑桃5 C.梅花6 D.红桃7
7.已知A(﹣2,0),B(0,3),将线段AB平移后得到线段A'B',若点A的对应点A'的坐标为(2,b),点B的对应点B'的坐标为(a,4),则a﹣b的值为( )
A.﹣3 B.﹣1 C.3 D.1
8.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为2米,那么小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.100米 B.98米 C.96米 D.94米
9.风力发电是一种将风能转化为电能的可再生能源技术.常见的风力发电机是由三片两两夹角120°的叶片底端相连组成(如图1).以扇叶重合处为坐标原点,水平方向为x轴建立平面直角坐标系(如图2),若某型号风力发电机的叶片每秒钟绕点O逆时针转动60°,点A初始位置横坐标为﹣1,OA与y轴正半轴夹角为30°,则第2024秒时,点A的坐标为( )
A. B. C.(2,0) D.(﹣1,﹣2)
(9题图) (10题图)
10.如图,直角△ABC中,∠ACB=90°,∠A=30°,BC=4,点E是边AC上一点,将BE绕点B顺时针旋转60°到点F,则CF长的最小值是( )
A. B.2 C. D.
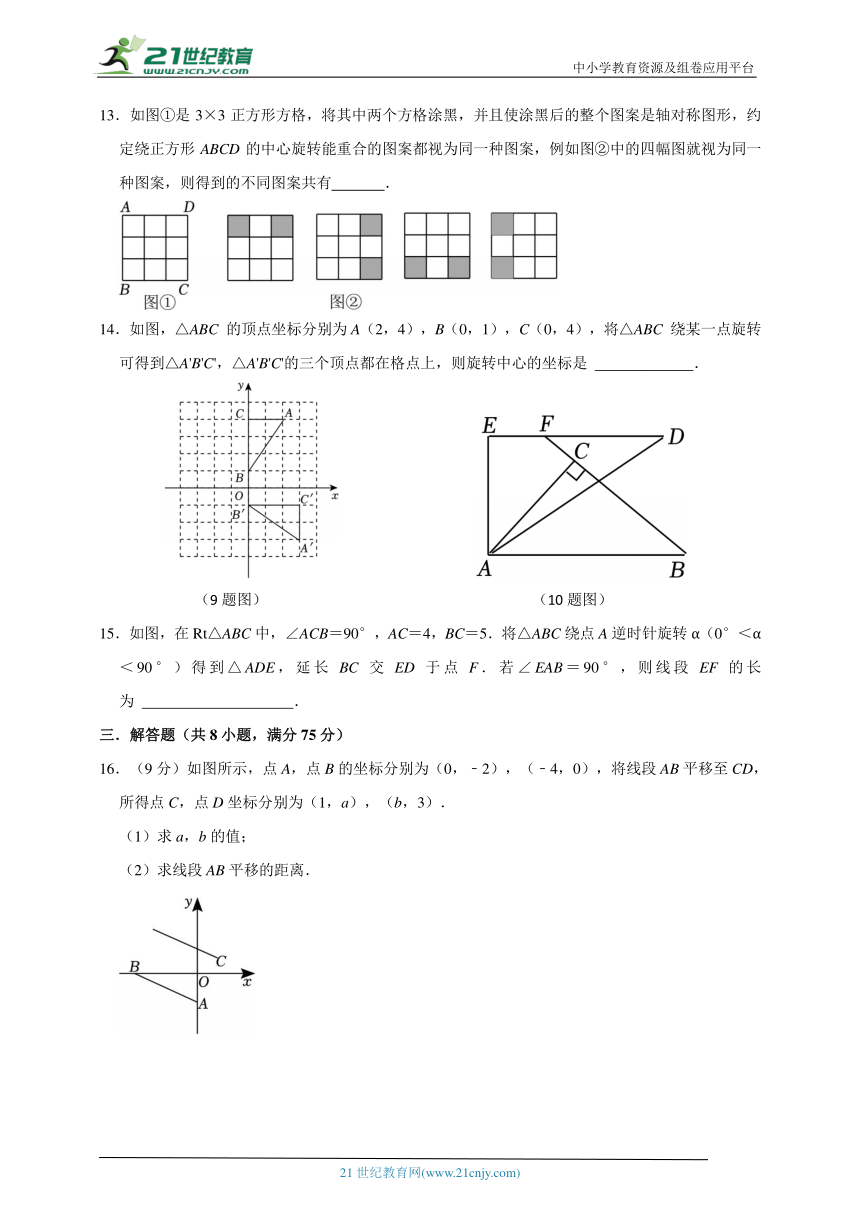
二.填空题(共5小题,满分15分,每小题3分)
11.若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是 .
12.如图,△ABC和△DBC都是边长为1的等边三角形,点B1在BC边上,将△DBC沿BC方向平移到△D1B1C1的位置.当四边形ABD1C1为矩形时,平移距离BB1= .
13.如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有 .
14.如图,△ABC 的顶点坐标分别为A(2,4),B(0,1),C(0,4),将△ABC 绕某一点旋转可得到△A'B'C',△A'B'C'的三个顶点都在格点上,则旋转中心的坐标是 .
(9题图) (10题图)
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.将△ABC绕点A逆时针旋转α(0°<α<90°)得到△ADE,延长BC交ED于点F.若∠EAB=90°,则线段EF的长为 .
三.解答题(共8小题,满分75分)
16.(9分)如图所示,点A,点B的坐标分别为(0,﹣2),(﹣4,0),将线段AB平移至CD,所得点C,点D坐标分别为(1,a),(b,3).
(1)求a,b的值;
(2)求线段AB平移的距离.
17.(9分)如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
18.(9分)(1)利用一副三角板可以画出一些特殊角,在①135°②120°③75°④150°⑤35°⑥15°六个角中,利用一副三角板画不出来的特殊角是 ;(填序号)
(2)如图①,先用三角板画出了直线EF,然后将一副三角板拼接在一起,其中45°角(∠AOB)的顶点与60°角(∠COD)的顶点互相重合,且边OA、OC都在直线EF上(图①),求∠BOD的度数;
(3)固定图①中三角板COD不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(如图②),当OB平分∠EOD时,求旋转角α的度数.
19.(9分)如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠AGE=79°,∠C=25°,则∠FAC为 度.
20.(9分)如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点B′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的;
(2)连接BC′,直接写出∠CBC′与∠B′C′O之间的数量关系 ;
(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.
21.(9分)综合与实践
在综合实践课上,白老师带领同学们为我市劳动公园的三块空地提供铺草和设计小路的方案,三块长方形空地的长都为30m,宽都为20m.白老师的设计方案如图1所示,阴影部分为一条平行四边形小路,EF=1m,长方形除去阴影部分后剩余部分为草地.
数学思考:
(1)求图1中草地的面积.
深入探究:
(2)白老师让同学们开发想象并完成本组的设计,并让小组成员提出相关的问题
①“善思小组”提出问题:设计方案如图2所示,有两条宽均为1米的小路(图中阴影部分),其余部分为草地,求草地的面积,请你解答此问题.
②“智慧小组”提出问题:设计方案如图3所示,阴影部分为草地,非阴影部分为1米宽的小路,沿着小路的中间从入口P处走到出口Q处,求所走的路线(图中虚线)长.请你思考此问题,并直接写出结果.
22.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,AD=5,BE=2,求线段DE的长.
23.(11分)在平面直角坐标系,△ABO为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD.AD,BD分别交y轴于点E,P.
(1)如图1,若点B在x轴的负半轴上,则∠BDO= °(直接写结果);
(2)如图2,将△ABO绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为α(60°<α<90°).
①补全图形;
②求∠BDO的度数(用含α的式子表示);
③写出线段BP,PE,PO间的等量关系,并证明你的结论.
参考答案
1. 选择题
1.解:A是轴对称图形,但不是中心对称图形,则A不符合题意,
B既是轴对称图形又是中心对称图形,则B符合题意,
C是轴对称图形,但不是中心对称图形,则C不符合题意,
D是轴对称图形,但不是中心对称图形,则D不符合题意,
选:B.
2.解:由平移的性质可知:CF=BE=2,
选:A.
3.解:如图所示,
分别过点A和点B作x轴的垂线,垂足分别为M和N,
由旋转可知,
OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.
在△AOM和△OBN中,
,
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(﹣4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).
选:B.
4.解:∵在等腰直角三角形ABC中,∠B=90°,
将△ABC绕点A逆时针旋转60°后得到的△AB′C′,
∴∠BAC=45°,
∴∠BAC′=45°+60°=105°.
选:B.
5.解:如图,连接BD,
∵将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,
∴∠BCD=90°,AB=AD,∠BAD=90°,
又CD=3,BC=1,
∴BD,
∴AD,
选:A.
6.解:因为牌中只有方块4是中心对称图形,所以旋转180度后,还是原来的样子.
选:A.
7.解:∵A(﹣2,0),B(0,3),将线段AB平移后得到线段A'B',若点A的对应点A'的坐标为(2,b),点B的对应点B'的坐标为(a,4),
∴﹣2+4=2,3+1=4,
即0+4=a,0+1=b,
解得:a=4,b=1,
∴a﹣b=4﹣1=3,
选:C.
8.解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD﹣2)×2,
图是矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,
则小明从出口A到出口B所走的路线长为50+(25﹣2)×2=96(米).
选:C.
9.解:因为360°÷60°=6,
所以每旋转六次,点A的坐标循环出现.
因为2024÷6=337余2,
所以第2024秒和第2秒点A的位置相同.
因为三片叶片的两两夹角为120°,
所以第2秒时点A的位置如图所示,
过点A′作x轴的垂线,垂足为M,
因为OA与y轴正半轴夹角为30°,
所以OA′与y轴负半轴夹角为30°,
所以点A和点A′关于x轴对称.
因为点A的横坐标为﹣1,
所以点A′的横坐标为﹣1,
所以OM=1.
MA′,
所以点A′的坐标为(﹣1,),
则第2024秒时,点A的坐标为().
选:B.
10.解:取AB的中点为点D,连接DE,过点D作DH⊥AC,垂足为H,
∴∠AHD=90°,
∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8,∠ABC=90°﹣∠A=60°,
∵点D是AB的中点,
∴AD=BDAB=4,
∴DHAD=2,
由旋转得:BE=BF,∠EBF=60°,
∴∠EBF=∠ABC=60°,
∴∠EBF﹣∠EBC=∠ABC﹣∠EBC,
∴∠ABE=∠CBF,
∵BD=BC=4,
∴△BDE≌△BCF(SAS),
∴DE=CF,
当DE⊥AC时,即当点E和点H重合时,DE有最小值,且最小值为2,
∴CF长的最小值是2,
选:B.
二.填空题
11.解:∵点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,
∴m﹣1=﹣3,2﹣n=﹣5,
解得:m=﹣2,n=7,
m+n=5.
答案为:5.
12.解:当移动距离BB1=1时,四边形ABD1C1是矩形.
理由:连接BC1,AD1,
∵△ABC,△DBC都是边长为1的等边三角形,
∴AB=B1D1=D1C1,=1,∠BC1D1=60°,
∵四边形ABD1C1为矩形时,
∴∠BD1C1=90°,
∴∠C1BD1=30°,
∴BC1=2D1C1=2,
∴BB1=BC1﹣B1C1=2﹣1=1.
答案为:1.
13.解:得到的不同图案有:
共6种.
14.解:如图所示,
点Q即为旋转中心,其坐标为(﹣1,0).
答案为:(﹣1,0).
15.解:连接AF,
∵∠ACB=90°,AC=4,BC=5,
∴,
由旋转的性质得AE=AC,∠E=∠ACB=90°,
∴∠E=∠ACF=90°,
∵AF=AF,
∴Rt△AFE≌Rt△AFC(HL),
∴EF=FC,∠EFA=∠CFA,
∵∠EAB=90°,
∴DE∥AB,
∴∠EFA=∠FAB,
∴∠BFA=∠FAB,
∴,
∴,
答案为:.
三.解答题
16.解:(1)∵点A,点B的坐标分别为(0,﹣2),(﹣4,0),点C,点D坐标分别为(1,a),(b,3),
∴1﹣0=1,3﹣0=3,
∴线段AB向上平移3个单位,再向右平移1个单位得线段CD,
∴a=﹣2+3=1,b=﹣4+1=﹣3;
(2)由(1)可知,点C坐标为(1,1),
∴线段AB平移的距离.
17.解:(1)由旋转的性质知AP′=AP=6,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△P′AP是等边三角形,
∴PP′=6;
(2)∵P′B=PC=10,PB=8,
∴P′B2=P′P2+PB2,
∴△P′PB为直角三角形,且∠P′PB=90°,
∴∠APB=∠P′PB+∠P′PA=90°+60°=150°.
18.解:(1)利用一副三角板可画出的角,应是15°角的整数倍,
∴①②③④⑥都可以画出来,但⑤画不出来;
答案为:⑤;
(2)根据题意得∠AOB=45°,∠COD=60°,
∴∠BOD=180°﹣∠AOB﹣∠COD=75°;
(3)∵∠COD=60°,
∴∠EOD=180°﹣∠COD=120°,
∵OB 平分∠EOD,
∴∠BOE=∠BOD=60°,
∴∠AOB=45°,
∴旋转角a=∠BOE﹣∠AOB=15°.
19.(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF,
由题意可得:AC=AF,
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)由(1)知,△ABC≌△AEF.
得∠F=∠C=25°.
在△AGF中,∠AGE是外角,
∠AGE=∠F+∠FAC,
∠AGE=∠F+∠FAC,
∴∠FAC=∠AGE﹣∠F=79°﹣25°=54°.
∴∠FAC为54°.
答案为:54.
20.解:(1)由图知,B(2,1),B′(﹣1,﹣2),
三角形A′B′C′是由三角形ABC向左平移3个单位,向下平移3个单位得到的;
(2)∠CBC′与∠B′C′O之间的数量关系∠CBC′﹣∠B′C′O=90°.
答案为:∠CBC′﹣∠B′C′O=90°;
(3)由(1)中的平移变换得a﹣1﹣3=2a﹣7,2b﹣5﹣3=4﹣b,
解得a=3,b=4.
a的值是3,b的值是4.
21.解:(1)根据题意草地的面积为:20×30﹣1×20=580(平方米);
答案为:580m2;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(30﹣1)×(20﹣1)=551(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30+20×2﹣2=68(米).
答案为:68m.
22.(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE;
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE=5﹣2=3.
23.解:(1)∵点A关于y轴的对称点为D,
∴∠DOE=∠EOA=90°﹣∠AOB=30°,
∴△OAD为等边三角形,
∴OA=OD,∠AOD=60°,
∴∠BOD=120°,
∵△OAB是等边三角形,
∴OB=OA,
∴OB=OD,
∴∠BDO30°;
答案为:30;
(2)①如图1,
②∵∠AOE=∠DOE=α,∠AOB=60°,
∴∠BOD=360°﹣2α﹣60°=300°﹣2α,
∵BO=OD,
∴∠OBD=∠ODB,
∴;
③2PE=BP+PO.
证明:连接AP,作AQ∥y轴,交DP的延长线于点Q.
∵∠OBD=∠BDO=α﹣60°,
∴∠ABQ=180°﹣∠ABO﹣∠BDO=180°﹣α,
∵∠AOP=180°﹣∠AOE=180°﹣α,
∴∠ABQ=∠AOP,
∵AQ∥y轴,
∴∠Q=∠DPE=∠APE,
又∵AB=AO,
∴△AOP≌△ABQ(AAS),
∴AP=AQ,BQ=PO,∠BAQ=∠OAP,
∴∠PAQ=∠QAB+∠BAP=∠BAP+∠PAO=60°,
∴△APQ为等边三角形,
∴AP=AQ=PQ=BP+BQ=BP+PO.
∵PA=PD,
∴PQ=DP.
∵EA=ED,
∴AQ=2EP,
∴2PE=BP+PO.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第3章 图形的平移与旋转 能力提升测试题
考试范围:第3章 图形的平移与旋转;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )
A.2 B.2.5 C.3 D.5
3.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
(2题图) (3题图) (4题图) (5题图)
4.如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
A.60° B.105° C.120° D.135°
5.如图,将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,若CD=3,BC=1,则AD的长为( )
A. B. C.2 D.
6.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把其中一张扑克牌旋转180°.魔术师解除蒙具后,看到4张牌如图②所示.被旋转过的牌是( )
A.方块4 B.黑桃5 C.梅花6 D.红桃7
7.已知A(﹣2,0),B(0,3),将线段AB平移后得到线段A'B',若点A的对应点A'的坐标为(2,b),点B的对应点B'的坐标为(a,4),则a﹣b的值为( )
A.﹣3 B.﹣1 C.3 D.1
8.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为2米,那么小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.100米 B.98米 C.96米 D.94米
9.风力发电是一种将风能转化为电能的可再生能源技术.常见的风力发电机是由三片两两夹角120°的叶片底端相连组成(如图1).以扇叶重合处为坐标原点,水平方向为x轴建立平面直角坐标系(如图2),若某型号风力发电机的叶片每秒钟绕点O逆时针转动60°,点A初始位置横坐标为﹣1,OA与y轴正半轴夹角为30°,则第2024秒时,点A的坐标为( )
A. B. C.(2,0) D.(﹣1,﹣2)
(9题图) (10题图)
10.如图,直角△ABC中,∠ACB=90°,∠A=30°,BC=4,点E是边AC上一点,将BE绕点B顺时针旋转60°到点F,则CF长的最小值是( )
A. B.2 C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是 .
12.如图,△ABC和△DBC都是边长为1的等边三角形,点B1在BC边上,将△DBC沿BC方向平移到△D1B1C1的位置.当四边形ABD1C1为矩形时,平移距离BB1= .
13.如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有 .
14.如图,△ABC 的顶点坐标分别为A(2,4),B(0,1),C(0,4),将△ABC 绕某一点旋转可得到△A'B'C',△A'B'C'的三个顶点都在格点上,则旋转中心的坐标是 .
(9题图) (10题图)
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.将△ABC绕点A逆时针旋转α(0°<α<90°)得到△ADE,延长BC交ED于点F.若∠EAB=90°,则线段EF的长为 .
三.解答题(共8小题,满分75分)
16.(9分)如图所示,点A,点B的坐标分别为(0,﹣2),(﹣4,0),将线段AB平移至CD,所得点C,点D坐标分别为(1,a),(b,3).
(1)求a,b的值;
(2)求线段AB平移的距离.
17.(9分)如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
18.(9分)(1)利用一副三角板可以画出一些特殊角,在①135°②120°③75°④150°⑤35°⑥15°六个角中,利用一副三角板画不出来的特殊角是 ;(填序号)
(2)如图①,先用三角板画出了直线EF,然后将一副三角板拼接在一起,其中45°角(∠AOB)的顶点与60°角(∠COD)的顶点互相重合,且边OA、OC都在直线EF上(图①),求∠BOD的度数;
(3)固定图①中三角板COD不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(如图②),当OB平分∠EOD时,求旋转角α的度数.
19.(9分)如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠AGE=79°,∠C=25°,则∠FAC为 度.
20.(9分)如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点B′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的;
(2)连接BC′,直接写出∠CBC′与∠B′C′O之间的数量关系 ;
(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.
21.(9分)综合与实践
在综合实践课上,白老师带领同学们为我市劳动公园的三块空地提供铺草和设计小路的方案,三块长方形空地的长都为30m,宽都为20m.白老师的设计方案如图1所示,阴影部分为一条平行四边形小路,EF=1m,长方形除去阴影部分后剩余部分为草地.
数学思考:
(1)求图1中草地的面积.
深入探究:
(2)白老师让同学们开发想象并完成本组的设计,并让小组成员提出相关的问题
①“善思小组”提出问题:设计方案如图2所示,有两条宽均为1米的小路(图中阴影部分),其余部分为草地,求草地的面积,请你解答此问题.
②“智慧小组”提出问题:设计方案如图3所示,阴影部分为草地,非阴影部分为1米宽的小路,沿着小路的中间从入口P处走到出口Q处,求所走的路线(图中虚线)长.请你思考此问题,并直接写出结果.
22.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,AD=5,BE=2,求线段DE的长.
23.(11分)在平面直角坐标系,△ABO为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD.AD,BD分别交y轴于点E,P.
(1)如图1,若点B在x轴的负半轴上,则∠BDO= °(直接写结果);
(2)如图2,将△ABO绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为α(60°<α<90°).
①补全图形;
②求∠BDO的度数(用含α的式子表示);
③写出线段BP,PE,PO间的等量关系,并证明你的结论.
参考答案
1. 选择题
1.解:A是轴对称图形,但不是中心对称图形,则A不符合题意,
B既是轴对称图形又是中心对称图形,则B符合题意,
C是轴对称图形,但不是中心对称图形,则C不符合题意,
D是轴对称图形,但不是中心对称图形,则D不符合题意,
选:B.
2.解:由平移的性质可知:CF=BE=2,
选:A.
3.解:如图所示,
分别过点A和点B作x轴的垂线,垂足分别为M和N,
由旋转可知,
OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.
在△AOM和△OBN中,
,
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(﹣4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).
选:B.
4.解:∵在等腰直角三角形ABC中,∠B=90°,
将△ABC绕点A逆时针旋转60°后得到的△AB′C′,
∴∠BAC=45°,
∴∠BAC′=45°+60°=105°.
选:B.
5.解:如图,连接BD,
∵将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,
∴∠BCD=90°,AB=AD,∠BAD=90°,
又CD=3,BC=1,
∴BD,
∴AD,
选:A.
6.解:因为牌中只有方块4是中心对称图形,所以旋转180度后,还是原来的样子.
选:A.
7.解:∵A(﹣2,0),B(0,3),将线段AB平移后得到线段A'B',若点A的对应点A'的坐标为(2,b),点B的对应点B'的坐标为(a,4),
∴﹣2+4=2,3+1=4,
即0+4=a,0+1=b,
解得:a=4,b=1,
∴a﹣b=4﹣1=3,
选:C.
8.解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD﹣2)×2,
图是矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,
则小明从出口A到出口B所走的路线长为50+(25﹣2)×2=96(米).
选:C.
9.解:因为360°÷60°=6,
所以每旋转六次,点A的坐标循环出现.
因为2024÷6=337余2,
所以第2024秒和第2秒点A的位置相同.
因为三片叶片的两两夹角为120°,
所以第2秒时点A的位置如图所示,
过点A′作x轴的垂线,垂足为M,
因为OA与y轴正半轴夹角为30°,
所以OA′与y轴负半轴夹角为30°,
所以点A和点A′关于x轴对称.
因为点A的横坐标为﹣1,
所以点A′的横坐标为﹣1,
所以OM=1.
MA′,
所以点A′的坐标为(﹣1,),
则第2024秒时,点A的坐标为().
选:B.
10.解:取AB的中点为点D,连接DE,过点D作DH⊥AC,垂足为H,
∴∠AHD=90°,
∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8,∠ABC=90°﹣∠A=60°,
∵点D是AB的中点,
∴AD=BDAB=4,
∴DHAD=2,
由旋转得:BE=BF,∠EBF=60°,
∴∠EBF=∠ABC=60°,
∴∠EBF﹣∠EBC=∠ABC﹣∠EBC,
∴∠ABE=∠CBF,
∵BD=BC=4,
∴△BDE≌△BCF(SAS),
∴DE=CF,
当DE⊥AC时,即当点E和点H重合时,DE有最小值,且最小值为2,
∴CF长的最小值是2,
选:B.
二.填空题
11.解:∵点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,
∴m﹣1=﹣3,2﹣n=﹣5,
解得:m=﹣2,n=7,
m+n=5.
答案为:5.
12.解:当移动距离BB1=1时,四边形ABD1C1是矩形.
理由:连接BC1,AD1,
∵△ABC,△DBC都是边长为1的等边三角形,
∴AB=B1D1=D1C1,=1,∠BC1D1=60°,
∵四边形ABD1C1为矩形时,
∴∠BD1C1=90°,
∴∠C1BD1=30°,
∴BC1=2D1C1=2,
∴BB1=BC1﹣B1C1=2﹣1=1.
答案为:1.
13.解:得到的不同图案有:
共6种.
14.解:如图所示,
点Q即为旋转中心,其坐标为(﹣1,0).
答案为:(﹣1,0).
15.解:连接AF,
∵∠ACB=90°,AC=4,BC=5,
∴,
由旋转的性质得AE=AC,∠E=∠ACB=90°,
∴∠E=∠ACF=90°,
∵AF=AF,
∴Rt△AFE≌Rt△AFC(HL),
∴EF=FC,∠EFA=∠CFA,
∵∠EAB=90°,
∴DE∥AB,
∴∠EFA=∠FAB,
∴∠BFA=∠FAB,
∴,
∴,
答案为:.
三.解答题
16.解:(1)∵点A,点B的坐标分别为(0,﹣2),(﹣4,0),点C,点D坐标分别为(1,a),(b,3),
∴1﹣0=1,3﹣0=3,
∴线段AB向上平移3个单位,再向右平移1个单位得线段CD,
∴a=﹣2+3=1,b=﹣4+1=﹣3;
(2)由(1)可知,点C坐标为(1,1),
∴线段AB平移的距离.
17.解:(1)由旋转的性质知AP′=AP=6,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△P′AP是等边三角形,
∴PP′=6;
(2)∵P′B=PC=10,PB=8,
∴P′B2=P′P2+PB2,
∴△P′PB为直角三角形,且∠P′PB=90°,
∴∠APB=∠P′PB+∠P′PA=90°+60°=150°.
18.解:(1)利用一副三角板可画出的角,应是15°角的整数倍,
∴①②③④⑥都可以画出来,但⑤画不出来;
答案为:⑤;
(2)根据题意得∠AOB=45°,∠COD=60°,
∴∠BOD=180°﹣∠AOB﹣∠COD=75°;
(3)∵∠COD=60°,
∴∠EOD=180°﹣∠COD=120°,
∵OB 平分∠EOD,
∴∠BOE=∠BOD=60°,
∴∠AOB=45°,
∴旋转角a=∠BOE﹣∠AOB=15°.
19.(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF,
由题意可得:AC=AF,
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)由(1)知,△ABC≌△AEF.
得∠F=∠C=25°.
在△AGF中,∠AGE是外角,
∠AGE=∠F+∠FAC,
∠AGE=∠F+∠FAC,
∴∠FAC=∠AGE﹣∠F=79°﹣25°=54°.
∴∠FAC为54°.
答案为:54.
20.解:(1)由图知,B(2,1),B′(﹣1,﹣2),
三角形A′B′C′是由三角形ABC向左平移3个单位,向下平移3个单位得到的;
(2)∠CBC′与∠B′C′O之间的数量关系∠CBC′﹣∠B′C′O=90°.
答案为:∠CBC′﹣∠B′C′O=90°;
(3)由(1)中的平移变换得a﹣1﹣3=2a﹣7,2b﹣5﹣3=4﹣b,
解得a=3,b=4.
a的值是3,b的值是4.
21.解:(1)根据题意草地的面积为:20×30﹣1×20=580(平方米);
答案为:580m2;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(30﹣1)×(20﹣1)=551(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30+20×2﹣2=68(米).
答案为:68m.
22.(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE;
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE=5﹣2=3.
23.解:(1)∵点A关于y轴的对称点为D,
∴∠DOE=∠EOA=90°﹣∠AOB=30°,
∴△OAD为等边三角形,
∴OA=OD,∠AOD=60°,
∴∠BOD=120°,
∵△OAB是等边三角形,
∴OB=OA,
∴OB=OD,
∴∠BDO30°;
答案为:30;
(2)①如图1,
②∵∠AOE=∠DOE=α,∠AOB=60°,
∴∠BOD=360°﹣2α﹣60°=300°﹣2α,
∵BO=OD,
∴∠OBD=∠ODB,
∴;
③2PE=BP+PO.
证明:连接AP,作AQ∥y轴,交DP的延长线于点Q.
∵∠OBD=∠BDO=α﹣60°,
∴∠ABQ=180°﹣∠ABO﹣∠BDO=180°﹣α,
∵∠AOP=180°﹣∠AOE=180°﹣α,
∴∠ABQ=∠AOP,
∵AQ∥y轴,
∴∠Q=∠DPE=∠APE,
又∵AB=AO,
∴△AOP≌△ABQ(AAS),
∴AP=AQ,BQ=PO,∠BAQ=∠OAP,
∴∠PAQ=∠QAB+∠BAP=∠BAP+∠PAO=60°,
∴△APQ为等边三角形,
∴AP=AQ=PQ=BP+BQ=BP+PO.
∵PA=PD,
∴PQ=DP.
∵EA=ED,
∴AQ=2EP,
∴2PE=BP+PO.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
