7.3 同底数幂的除法 课件(共30张PPT)
文档属性
| 名称 | 7.3 同底数幂的除法 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 21:31:21 | ||
图片预览











文档简介
(共30张PPT)
7.3 同底数幂的除法
第7章 幂的运算
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.了解同底数幂的除法的运算性质,并会用符号表示.
2.会正确运用同底数幂的除法的运算性质进行运算,发展运算能力.
3.了解零指数幂及负整数指数幂的意义.
4.会用科学记数法表示绝对值小于1的数,并解决相关实际问题,培养应用意识.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
同底数幂的除法的运算性质
文字语言 推导 符号表示
同底数幂 相除,底数 不变,指数 相减. _________________________________________________________________________________
,,是正整数, .
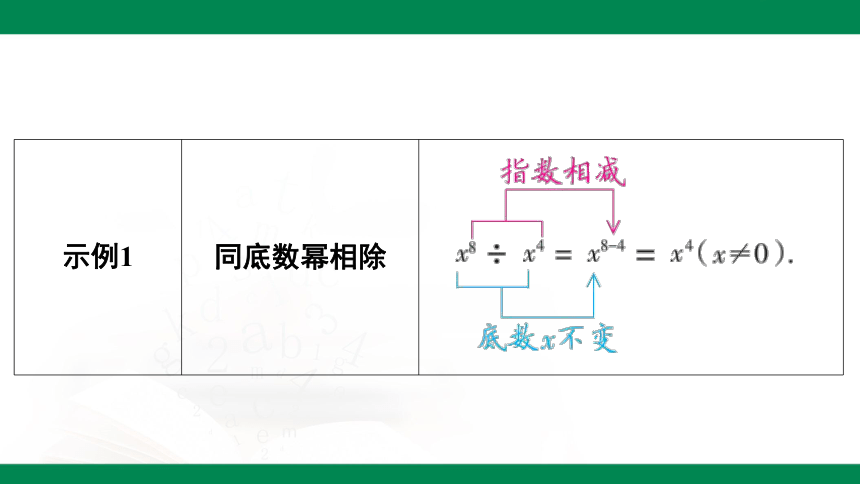
示例1 同底数幂相除 _______________________________________________________________________
教材延伸
同底数幂的除法的推广与逆用
(1)同底数幂的除法的运算性质可以推广到三个或三个以上的同
底数幂相除,如
(2)同底数幂的除法的运算性质的逆用:
,
典例1 计算:
(1) ;
解: .
(2) ;
解: .
(3) ;
解:.
(4) .
解: .
零指数幂的性质
文字语 言 推导 符号表示
任何不 等于0 的数的 0次幂 等于1. 如果把公式,, 都 是正整数,且推广到 的情形, 那么有 ,而 ,所以规定 .
.
..
典例2 若,则 的取值范围为( )
B
A. B. C. D.
解析:因为,所以,所以 .
1.负整数指数幂的性质
文字语言:任何不等于0的数的
符号表示:
2.整数指数幂的运算性质
学习了零指数幂和负整数指数幂后,指数的取值范围由正整数推广
到了全体整数,之前学过的所有幂的运算性质对整数指数幂都适用.
整数指数幂的运算性质可以归结为:
名称 式子表示
同底数幂的乘法 ,是整数 .
幂的乘方 ,是整数 .
积的乘方 是整数 .
同底数幂的除法 ,是整数, .
商的乘方 是整数, .
因为, ,所以同底数幂
的除法可以转化为同底数幂的乘法,商的乘方可转化为积的乘方.
这样,整数指数幂的运算性质可以合并为表格中的前3条.
典例3 计算:
(1) ;
解: .
(2) ;
解:.
.
(3) ;
解:
(底数为小数时,可先将小数化为分数的形式,再计算)
(4) ;
解: .
(运用同底数幂的除法的运算性质时,若指数是多项式,则指数相
减时要加上括号)
(5) .
解: .
1.用科学记数法表示绝对值小于1的数:一般地,用科学记数法可以
把一个绝对值小于1的数表示成的形式,其中,
是正整数.
2.用科学记数法表示绝对值小于1的数的步骤
(1)确定
数的符号一致,与指数的符号无关)
(2)确定
0数字前所有0的个数(包括小数点前面的那个0);②小数点向右移
动到第一个不为0的数字的后边,小数点移动了几位,
(3)将原数用科学记数法表示为 的形式(其中
, 是正整数).
示例2 用科学记数法表示绝 对值小于1的数 ________________________________________________________________________________
1. [2024平顶山月考]计算(-2 024)0=( A )
A. 1 B. 0
C. -1 D. -2 024
2. 计算 a4· a2÷ a2=( C )
A. a3 B. a2 C. a4 D. a5
A
C
3. 计算(- a2)3÷(- a )2=( B )
A. a2 B. - a4
C. - a2 D. a4
B
4. [2024烟台蓬莱区期中]( p - q )4÷( q - p )3= .
5. 若( x2)3÷ xm = x4,则 m = .
q - p
2
6. [母题教材P104练习T1] 计算:
(1)(- m )8÷(- m )3; (2)( xy )7÷( xy )4;
(3) x2 m+2÷ xm+2; (4) x6÷ x2· x .
【解】(1)(- m )8÷(- m )3=(- m )5=- m5.
(2)( xy )7÷( xy )4=( xy )3= x3 y3.
(3) x2 m+2÷ xm+2= xm .
(4) x6÷ x2· x = x4· x = x5.
7. 已知 xm =3, xn =5,则 x3 m-2 n 等于( A )
A. B.
C. D. 52
A
8. [2023石家庄裕华区二模]计算 的值为
( C )
A. m2 B. 2 m
C. mm D. m2- m
C
9. 若( a -1) a+2=1,则 a = .
【点拨】
分三种情况讨论:①当 a -1≠0时,要使( a -1) a+2
=1,则 a +2=0,解得 a =-2,此时原式成立;②当 a
-1=1时,解得 a =2,此时原式成立;③当 a -1=-1
时,解得 a =0,此时原式成立.综上所述, a 的值为-2
或2或0.
-2或2或0
10. 若2 m ÷4 n =32,则2 m -4 n -3的值为 .
【点拨】
∵2 m ÷4 n =32,∴2 m ÷22 n =25,∴2 m-2 n =25,
∴ m -2 n =5,∴2 m -4 n -3=2( m -2 n )-3=2×5-
3=10-3=7.
7
11. [母题教材P105习题T9] 计算机存储容量的基本单位
是B(字节),通常还用KB(千字节)、MB(兆字节)、
GB(吉字节)等作为存储容量的计量单位.已知1 KB=
210 B,1 MB=210 KB,1 GB=210 MB,那么237 B
相当于多少吉字节?
谢谢观看!
7.3 同底数幂的除法
第7章 幂的运算
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.了解同底数幂的除法的运算性质,并会用符号表示.
2.会正确运用同底数幂的除法的运算性质进行运算,发展运算能力.
3.了解零指数幂及负整数指数幂的意义.
4.会用科学记数法表示绝对值小于1的数,并解决相关实际问题,培养应用意识.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
同底数幂的除法的运算性质
文字语言 推导 符号表示
同底数幂 相除,底数 不变,指数 相减. _________________________________________________________________________________
,,是正整数, .
示例1 同底数幂相除 _______________________________________________________________________
教材延伸
同底数幂的除法的推广与逆用
(1)同底数幂的除法的运算性质可以推广到三个或三个以上的同
底数幂相除,如
(2)同底数幂的除法的运算性质的逆用:
典例1 计算:
(1) ;
解: .
(2) ;
解: .
(3) ;
解:.
(4) .
解: .
零指数幂的性质
文字语 言 推导 符号表示
任何不 等于0 的数的 0次幂 等于1. 如果把公式,, 都 是正整数,且推广到 的情形, 那么有 ,而 ,所以规定 .
.
..
典例2 若,则 的取值范围为( )
B
A. B. C. D.
解析:因为,所以,所以 .
1.负整数指数幂的性质
文字语言:任何不等于0的数的
符号表示:
2.整数指数幂的运算性质
学习了零指数幂和负整数指数幂后,指数的取值范围由正整数推广
到了全体整数,之前学过的所有幂的运算性质对整数指数幂都适用.
整数指数幂的运算性质可以归结为:
名称 式子表示
同底数幂的乘法 ,是整数 .
幂的乘方 ,是整数 .
积的乘方 是整数 .
同底数幂的除法 ,是整数, .
商的乘方 是整数, .
因为, ,所以同底数幂
的除法可以转化为同底数幂的乘法,商的乘方可转化为积的乘方.
这样,整数指数幂的运算性质可以合并为表格中的前3条.
典例3 计算:
(1) ;
解: .
(2) ;
解:.
.
(3) ;
解:
(底数为小数时,可先将小数化为分数的形式,再计算)
(4) ;
解: .
(运用同底数幂的除法的运算性质时,若指数是多项式,则指数相
减时要加上括号)
(5) .
解: .
1.用科学记数法表示绝对值小于1的数:一般地,用科学记数法可以
把一个绝对值小于1的数表示成的形式,其中,
是正整数.
2.用科学记数法表示绝对值小于1的数的步骤
(1)确定
数的符号一致,与指数的符号无关)
(2)确定
0数字前所有0的个数(包括小数点前面的那个0);②小数点向右移
动到第一个不为0的数字的后边,小数点移动了几位,
(3)将原数用科学记数法表示为 的形式(其中
, 是正整数).
示例2 用科学记数法表示绝 对值小于1的数 ________________________________________________________________________________
1. [2024平顶山月考]计算(-2 024)0=( A )
A. 1 B. 0
C. -1 D. -2 024
2. 计算 a4· a2÷ a2=( C )
A. a3 B. a2 C. a4 D. a5
A
C
3. 计算(- a2)3÷(- a )2=( B )
A. a2 B. - a4
C. - a2 D. a4
B
4. [2024烟台蓬莱区期中]( p - q )4÷( q - p )3= .
5. 若( x2)3÷ xm = x4,则 m = .
q - p
2
6. [母题教材P104练习T1] 计算:
(1)(- m )8÷(- m )3; (2)( xy )7÷( xy )4;
(3) x2 m+2÷ xm+2; (4) x6÷ x2· x .
【解】(1)(- m )8÷(- m )3=(- m )5=- m5.
(2)( xy )7÷( xy )4=( xy )3= x3 y3.
(3) x2 m+2÷ xm+2= xm .
(4) x6÷ x2· x = x4· x = x5.
7. 已知 xm =3, xn =5,则 x3 m-2 n 等于( A )
A. B.
C. D. 52
A
8. [2023石家庄裕华区二模]计算 的值为
( C )
A. m2 B. 2 m
C. mm D. m2- m
C
9. 若( a -1) a+2=1,则 a = .
【点拨】
分三种情况讨论:①当 a -1≠0时,要使( a -1) a+2
=1,则 a +2=0,解得 a =-2,此时原式成立;②当 a
-1=1时,解得 a =2,此时原式成立;③当 a -1=-1
时,解得 a =0,此时原式成立.综上所述, a 的值为-2
或2或0.
-2或2或0
10. 若2 m ÷4 n =32,则2 m -4 n -3的值为 .
【点拨】
∵2 m ÷4 n =32,∴2 m ÷22 n =25,∴2 m-2 n =25,
∴ m -2 n =5,∴2 m -4 n -3=2( m -2 n )-3=2×5-
3=10-3=7.
7
11. [母题教材P105习题T9] 计算机存储容量的基本单位
是B(字节),通常还用KB(千字节)、MB(兆字节)、
GB(吉字节)等作为存储容量的计量单位.已知1 KB=
210 B,1 MB=210 KB,1 GB=210 MB,那么237 B
相当于多少吉字节?
谢谢观看!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
