8.2 单项式乘多项式 课件(共30张PPT)
文档属性
| 名称 | 8.2 单项式乘多项式 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 21:38:38 | ||
图片预览







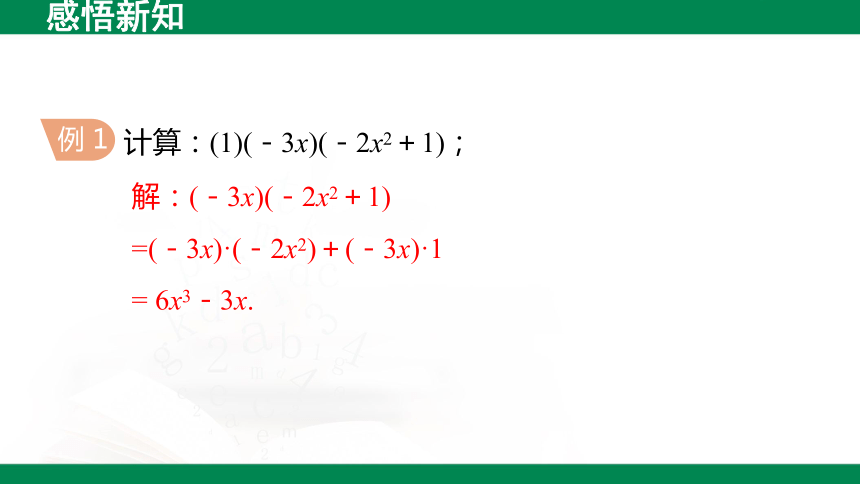




文档简介
(共30张PPT)
8.2 单项式乘多项式
第8章 整式乘法
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解单项式乘多项式的运算法则,能熟练地进行单项式乘多项式的
计算,发展运算能力.
2.体会乘法分配律的作用和转化的思想,提升分析问题的能力及语言表达能力.
3.经历探索单项式乘多项式运算法则的过程,感悟数形结合思想,知道使用符号可以进行推理运算,得到的结论具有一般性,培养抽象能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
单项式乘多项式
感悟新知
1
1. 运算法则:单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加.
用字母表示为 m(a+b+c)=ma+mb+mc.其中m、a、b、c都是单项式.
感悟新知
2. 单项式与多项式相乘的几何解释:如图8.2-1,大长方形的面积可以表示为m(a+b+c),也可以视为三个小长方形的面积之和,所以大长方形的面积也可以表示为
ma+mb+mc. 所以m(a+b+c)=ma+mb+mc.
感悟新知
3. 单项式与多项式相乘的步骤
(1)根据乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;
(2)将单项式与单项式相乘的结果相加.
知1-讲
感悟新知
特别解读
1. 单项式与多项式相乘,实际上是利用乘法分配律将其转化为单项式与单项式相乘.
2. 单项式与多项式相乘的结果是一个多项式,其项数与因式中多项式的项数相同.
3. 单项式与多项式相乘时,要把单项式与多项式里的每一项都相乘,不要漏乘、多乘.
感悟新知
计算:(1)(-3x)(-2x2+1);
例 1
解:(-3x)(-2x2+1)
=(-3x)·(-2x2)+(-3x)·1
= 6x3-3x.
感悟新知
知1-练
(2)(3xy2-6xy-1)· xy.
解题秘方:用单项式乘多项式的法则进行计算.
解:(3xy2-6xy-1)· xy
=3xy2· xy+(-6xy)· xy+(-1)· xy
=x2y3-2x2y2- xy.
感悟新知
知1-练
特别警示
1. 单项式乘多项式,当多项式的某项为1 时, 千万不能出现漏乘的情况.
2. 多项式的各项都包括它前面的符号,(2)中多项式的项有3xy2,-6xy,-1,计算时要将这三项分别与xy相乘.
典例 计算:
(1) ;
解: .
.
(2) .
解:
.
1. 化简: a ( a -2)+4 a =( A )
A. a2+2 a B. a2+6 a
C. a2-6 a D. a2+4 a -2
2. 方程-2 x ( x -1)+ x (2 x -5)=3的解是( D )
A. x =1 B. x =2
C. x = D. x =-1
A
D
3. 一个长方体的长、宽、高分别为3 x -4,2 x 和 x ,则它的
体积等于( C )
A. 3 x3-4 x B. 6 x3-4 x
C. 6 x3-8 x2 D. 6 x2-8 x
4. [2024北京海淀区期中]已知2 a2-7 a -1=0,则代数式 a
(2 a -7)+5的值为( A )
A. 6 B. 5 C. 4 D. -4
C
A
5. 数学课上,老师讲了单项式与多项式相乘,回到家,小丽
拿出课堂笔记复习,突然发现一道题:-3 x2(2 x -□+1)
=-6 x3+3 x2 y -3 x2,“□”的地方被墨水污染了,则
“□”上应是 .
6. [学科素养 逻辑推理] n 为自然数,那么式子 n (2 n +1)-2
n ( n -1)能否被3整除?
【解】原式=2 n2+ n -2 n2+2 n =3 n ,则代数式 n (2 n
+1)-2 n ( n -1)能被3整除.
y
7. [母题教材P100例5] 计算:
(1)-6 a · ;
【解】原式=-6 a · -(-6 a )· a +(-6 a )×2
=3 a3+2 a2-12 a .
(2)(5 mn2-4 m2 n )·(-2 mn );
【解】原式=5 mn2·(-2 mn )-4 m2 n ·(-2 mn )=-10
m2 n3+8 m3 n2.
(3) x2( x -1)- x ( x2+ x -1);
【解】原式= x3- x2- x3- x2+ x = x -2 x2.
(4)-2 a2· -5 ab · .
【解】原式=- a3 b -2 a2 b2-2 a3 b +5 a2 b2=-3 a3 b
+3 a2 b2.
8. 已知有理数 a , b , c 满足| a - b -3|+( b +1)2+
| c -1|=0,先化简,再求值:(-3 ab )·( a2 c -6 b2 c ).
【解】(-3 ab )·( a2 c -6 b2 c )=-3 a3 bc +18 ab3 c .
由| a - b -3|+( b +1)2+| c -1|=0,得
解得∴原式=-3×23×(-1)×
1+18×2×(-1)3×1=24-36=-12.
9. 已知( x4- n + ym+3)· xn = x4+ x2 y7,则 m + n 的值是
( D )
A. 3 B. 4 C. 5 D. 6
10. [2024蚌埠龙子湖区期中]要使 x ( x +2 a )+2 x -2 b = x2+6 x +8成立,则 a , b 的值分别为( C )
A. a =-2, b =-4 B. a =2, b =4
C. a =2, b =-4 D. a =-2, b =4
D
C
11. 要使( x2+ ax +5)(-6 x3)的展开式中不含 x4项,则 a 等于
( D )
A. 1 B. -1
C. D. 0
D
12. 定义 表示3 abc , 表示 xz + wy ,则 ×
的结果为( B )
A. 72 m2 n -45 mn2 B. 72 m2 n +45 mn2
C. 24 m2 n -15 mn2 D. 24 m2 n +15 mn2
B
13. 已知 A =-2 x2, B = x2-3 x -1, C =- x +1,则
A · B + A · C 的值为 .
14. 某同学在计算一个多项式乘-3 x2时,算成了加上-3x2,得到的答案是 x2- x +1,则正确的计算结果
是 .
-2 x4+8 x3
-12 x4+ x3-3 x2
【点拨】
由题意可得,原多项式为 x2- x +1+3 x2=4 x2-
x +1,故正确的计算结果应为-3 x2·(4 x2- x +1)=
-12 x4+ x3-3 x2.
15. (1)[母题教材P106习题T12] 一张长方形硬纸板的长为
(5 a2+4 b2)m,宽为6 a4 m,在它的四个角上分别剪去一个边长为 a3 m的小正方形,然后折成一个无盖的盒子,请你求出折成的无盖盒子所用硬纸板的面积;
【解】长方形硬纸板的面积是(5 a2+4 b2)·6 a4=(30 a6+
24 a4 b2)(m2),一个小正方形的面积是 = a6(m2),则折成的无盖盒子所用硬纸板的面积是30 a6+24 a4 b2-4× a6=(21 a6+24 a4 b2)(m2).
(2)如图,一块长方形地用来建造住宅、广场和商厦,求
这块地的面积.
【解】长方形地的长为(3 a +2 b )+
(2 a - b )=5 a + b ,宽为4 a ,
所以这块地的面积为4 a ·(5 a + b )=
20 a2+4 ab .
16. [整体思想]阅读下面的解题过程,并解决问题.
已知:2 ab2=3,求 ab ·(8 a2 b5+4 ab3-2 b )的值.
分析:因为满足2 ab2=3的 a , b 的值较多,优先考虑用
整体代入的思想,将2 ab2=3整体代入.
解: ab ·(8 a2 b5+4 ab3-2 b )
=8 a3 b6+4 a2 b4-2 ab2
=(2 ab2)3+(2 ab2)2-2 ab2
=33+32-3
=33.
请你结合上述思想解决问题:已知2 m2=5,求(4 m5-
2 m3+ m )·(-2 m )的值.
【解】∵2 m2=5,
∴(4 m5-2 m3+ m )·(-2 m )=-8 m6+4 m4-2 m2=-(2
m2)3+(2 m2)2-2 m2=-53+52-5=-105.
谢谢观看!
8.2 单项式乘多项式
第8章 整式乘法
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解单项式乘多项式的运算法则,能熟练地进行单项式乘多项式的
计算,发展运算能力.
2.体会乘法分配律的作用和转化的思想,提升分析问题的能力及语言表达能力.
3.经历探索单项式乘多项式运算法则的过程,感悟数形结合思想,知道使用符号可以进行推理运算,得到的结论具有一般性,培养抽象能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
单项式乘多项式
感悟新知
1
1. 运算法则:单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加.
用字母表示为 m(a+b+c)=ma+mb+mc.其中m、a、b、c都是单项式.
感悟新知
2. 单项式与多项式相乘的几何解释:如图8.2-1,大长方形的面积可以表示为m(a+b+c),也可以视为三个小长方形的面积之和,所以大长方形的面积也可以表示为
ma+mb+mc. 所以m(a+b+c)=ma+mb+mc.
感悟新知
3. 单项式与多项式相乘的步骤
(1)根据乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;
(2)将单项式与单项式相乘的结果相加.
知1-讲
感悟新知
特别解读
1. 单项式与多项式相乘,实际上是利用乘法分配律将其转化为单项式与单项式相乘.
2. 单项式与多项式相乘的结果是一个多项式,其项数与因式中多项式的项数相同.
3. 单项式与多项式相乘时,要把单项式与多项式里的每一项都相乘,不要漏乘、多乘.
感悟新知
计算:(1)(-3x)(-2x2+1);
例 1
解:(-3x)(-2x2+1)
=(-3x)·(-2x2)+(-3x)·1
= 6x3-3x.
感悟新知
知1-练
(2)(3xy2-6xy-1)· xy.
解题秘方:用单项式乘多项式的法则进行计算.
解:(3xy2-6xy-1)· xy
=3xy2· xy+(-6xy)· xy+(-1)· xy
=x2y3-2x2y2- xy.
感悟新知
知1-练
特别警示
1. 单项式乘多项式,当多项式的某项为1 时, 千万不能出现漏乘的情况.
2. 多项式的各项都包括它前面的符号,(2)中多项式的项有3xy2,-6xy,-1,计算时要将这三项分别与xy相乘.
典例 计算:
(1) ;
解: .
.
(2) .
解:
.
1. 化简: a ( a -2)+4 a =( A )
A. a2+2 a B. a2+6 a
C. a2-6 a D. a2+4 a -2
2. 方程-2 x ( x -1)+ x (2 x -5)=3的解是( D )
A. x =1 B. x =2
C. x = D. x =-1
A
D
3. 一个长方体的长、宽、高分别为3 x -4,2 x 和 x ,则它的
体积等于( C )
A. 3 x3-4 x B. 6 x3-4 x
C. 6 x3-8 x2 D. 6 x2-8 x
4. [2024北京海淀区期中]已知2 a2-7 a -1=0,则代数式 a
(2 a -7)+5的值为( A )
A. 6 B. 5 C. 4 D. -4
C
A
5. 数学课上,老师讲了单项式与多项式相乘,回到家,小丽
拿出课堂笔记复习,突然发现一道题:-3 x2(2 x -□+1)
=-6 x3+3 x2 y -3 x2,“□”的地方被墨水污染了,则
“□”上应是 .
6. [学科素养 逻辑推理] n 为自然数,那么式子 n (2 n +1)-2
n ( n -1)能否被3整除?
【解】原式=2 n2+ n -2 n2+2 n =3 n ,则代数式 n (2 n
+1)-2 n ( n -1)能被3整除.
y
7. [母题教材P100例5] 计算:
(1)-6 a · ;
【解】原式=-6 a · -(-6 a )· a +(-6 a )×2
=3 a3+2 a2-12 a .
(2)(5 mn2-4 m2 n )·(-2 mn );
【解】原式=5 mn2·(-2 mn )-4 m2 n ·(-2 mn )=-10
m2 n3+8 m3 n2.
(3) x2( x -1)- x ( x2+ x -1);
【解】原式= x3- x2- x3- x2+ x = x -2 x2.
(4)-2 a2· -5 ab · .
【解】原式=- a3 b -2 a2 b2-2 a3 b +5 a2 b2=-3 a3 b
+3 a2 b2.
8. 已知有理数 a , b , c 满足| a - b -3|+( b +1)2+
| c -1|=0,先化简,再求值:(-3 ab )·( a2 c -6 b2 c ).
【解】(-3 ab )·( a2 c -6 b2 c )=-3 a3 bc +18 ab3 c .
由| a - b -3|+( b +1)2+| c -1|=0,得
解得∴原式=-3×23×(-1)×
1+18×2×(-1)3×1=24-36=-12.
9. 已知( x4- n + ym+3)· xn = x4+ x2 y7,则 m + n 的值是
( D )
A. 3 B. 4 C. 5 D. 6
10. [2024蚌埠龙子湖区期中]要使 x ( x +2 a )+2 x -2 b = x2+6 x +8成立,则 a , b 的值分别为( C )
A. a =-2, b =-4 B. a =2, b =4
C. a =2, b =-4 D. a =-2, b =4
D
C
11. 要使( x2+ ax +5)(-6 x3)的展开式中不含 x4项,则 a 等于
( D )
A. 1 B. -1
C. D. 0
D
12. 定义 表示3 abc , 表示 xz + wy ,则 ×
的结果为( B )
A. 72 m2 n -45 mn2 B. 72 m2 n +45 mn2
C. 24 m2 n -15 mn2 D. 24 m2 n +15 mn2
B
13. 已知 A =-2 x2, B = x2-3 x -1, C =- x +1,则
A · B + A · C 的值为 .
14. 某同学在计算一个多项式乘-3 x2时,算成了加上-3x2,得到的答案是 x2- x +1,则正确的计算结果
是 .
-2 x4+8 x3
-12 x4+ x3-3 x2
【点拨】
由题意可得,原多项式为 x2- x +1+3 x2=4 x2-
x +1,故正确的计算结果应为-3 x2·(4 x2- x +1)=
-12 x4+ x3-3 x2.
15. (1)[母题教材P106习题T12] 一张长方形硬纸板的长为
(5 a2+4 b2)m,宽为6 a4 m,在它的四个角上分别剪去一个边长为 a3 m的小正方形,然后折成一个无盖的盒子,请你求出折成的无盖盒子所用硬纸板的面积;
【解】长方形硬纸板的面积是(5 a2+4 b2)·6 a4=(30 a6+
24 a4 b2)(m2),一个小正方形的面积是 = a6(m2),则折成的无盖盒子所用硬纸板的面积是30 a6+24 a4 b2-4× a6=(21 a6+24 a4 b2)(m2).
(2)如图,一块长方形地用来建造住宅、广场和商厦,求
这块地的面积.
【解】长方形地的长为(3 a +2 b )+
(2 a - b )=5 a + b ,宽为4 a ,
所以这块地的面积为4 a ·(5 a + b )=
20 a2+4 ab .
16. [整体思想]阅读下面的解题过程,并解决问题.
已知:2 ab2=3,求 ab ·(8 a2 b5+4 ab3-2 b )的值.
分析:因为满足2 ab2=3的 a , b 的值较多,优先考虑用
整体代入的思想,将2 ab2=3整体代入.
解: ab ·(8 a2 b5+4 ab3-2 b )
=8 a3 b6+4 a2 b4-2 ab2
=(2 ab2)3+(2 ab2)2-2 ab2
=33+32-3
=33.
请你结合上述思想解决问题:已知2 m2=5,求(4 m5-
2 m3+ m )·(-2 m )的值.
【解】∵2 m2=5,
∴(4 m5-2 m3+ m )·(-2 m )=-8 m6+4 m4-2 m2=-(2
m2)3+(2 m2)2-2 m2=-53+52-5=-105.
谢谢观看!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
