8.3 多项式乘多项式 课件(共30张PPT)
文档属性
| 名称 | 8.3 多项式乘多项式 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 21:40:03 | ||
图片预览











文档简介
(共30张PPT)
8.3 多项式乘多项式
第8章 整式乘法
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解多项式乘多项式的运算法则,能熟练运用法则进行多项式与多项式的乘法计算,发展运算能力.
2.在多项式与多项式乘法法则的推导过程中,体会转化思想,进一步
提升有条理地分析问题的能力与语言表达能力.
3.经历探索多项式乘多项式运算法则的过程,理解数与形的关系,知道使用符号可以进行推理运算,得到的结论具有一般性,培养抽象能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
多项式乘多项式
知1-讲
感悟新知
1
1. 多项式乘多项式的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
用字母表示为(a+b)(m+n)=am+bm+an+bn.
知1-讲
感悟新知
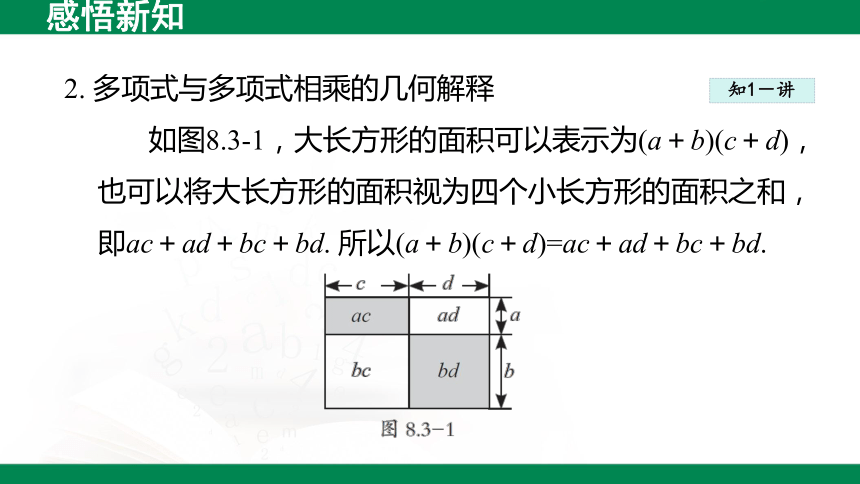
2. 多项式与多项式相乘的几何解释
如图8.3-1,大长方形的面积可以表示为(a+b)(c+d),也可以将大长方形的面积视为四个小长方形的面积之和,即ac+ad+bc+bd. 所以(a+b)(c+d)=ac+ad+bc+bd.
感悟新知
知1-练
计算:(1)(3x+2)(2x-3)
例 1
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=3x·2x+3x·(-3)+2·2x+2×(-3)
=6x2-9x+4x-6
=6x2-5x-6.
感悟新知
知1-练
(2)(x+2)(x2-2x+4).
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=x·x2+x·(-2x)+x·4+2·x2+2·(-2x)+2×4
=x3-2x2+4x+2x2-4x+8
=x3+8.
感悟新知
知1-练
(3)(n-1)(n+1).
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=n(n2+n-n-1)=n(n2-1)=n3-n.
感悟新知
知1-练
教你一招:用“箭头法”解多项式乘多项式的问题的方法:多项式与多项式相乘,为了做到不重不漏,可以用“箭头法”标注求解,如计算(x-2y)(5a-3b)时,可作标注: ,根据箭头指示,即可得到x·5a、x·(-3b)、(-2y)·5a、(-2y)·(-3b),把各项相加,继续求解即可.
感悟新知
知1-练
方法点拨
(x+a)(x+b)型的多项式乘法,直接用(x+a)·(x+b)=x2+(a+b)x+ab 计算更简便.
感悟新知
知1-练
另解
(2)可以将x2-2x+4 看成一个整体,利用分配律计算:(x+2)(x2-2x+4)=x(x2-2x+4)+2(x2-2x+4)=x3-2x2+4x+2x2-4x+8=x3+8.
典例 计算:
(1) ;
解:
(提示:有同类项的要合并同类项)
.
(2) ;
解:
.
(3) .
解:
1. [2024佛山顺德区期中]计算( x +5)( x -3)的结果是( C )
A. x2-15 B. x2+15
C. x2+2 x -15 D. x2-2 x -15
C
2. 观察下列两个多项式相乘的运算过程:根据你发现的规
律,若( x + a )( x + b )= x2-7 x +12,则 a , b 的值可能
分别是( A )
A. -3,-4 B. -3,4
C. 3,-4 D. 3,4
A
3. [2024沈阳沈河区期末]两个关于 x 的一次整式3 x +9与6 x
-8相乘,所得结果的一次项系数为( B )
A. 18 B. 30
C. 78 D. -72
B
4. 若(5 x -6)(2 x -3)= ax2+ bx + c ,则2 a + b - c 等于
( A )
A. -25 B. -11
C. 4 D. 11
A
5. [2024宿迁一模]若 x2-9=( x +3)( x + a ),则 a =
.
6. 已知 x + y =5, xy =-36,则( x -2)( y -2)的值为
.
-3
-42
7. [母题教材P102练习T1]计算:
(1)(-7 x2-8 y2)·(- x2+3 y2);
【解】原式=7 x4-21 x2 y2+8 x2 y2-24 y4=7 x4-13 x2
y2-24 y4.
(2)(3 x +2 y )(9 x2-6 xy +4 y2);
【解】原式=27 x3-18 x2 y +12 xy2+18 x2 y -12 xy2+
8 y3=27 x3+8 y3.
(3)(3 x -2 y )( y -3 x )-(2 x - y )(3 x + y ).
【解】原式=3 xy -9 x2-2 y2+6 xy -(6 x2+2 xy - 3 xy - y2)
=3 xy -9 x2-2 y2+6 xy -6 x2-2 xy +3 xy + y2
=10 xy -15 x2- y2.
8. 解方程或不等式:
(1)5 x ( x +2)-( x +1)( x -1)=4( x2-6);
【解】5 x ( x +2)-( x +1)( x -1)=4( x2-6),
5 x2+10 x -( x2- x + x -1)=4 x2-24,
5 x2+10 x - x2+1=4 x2-24,
10 x =-25,
x =-2.5.
(2)( x -3)( x -2)-2>( x +9)( x -1).
【解】( x -3)( x -2)-2>( x +9)( x -1),
x2-2 x -3 x +6-2> x2- x +9 x -9,
x2-5 x +4> x2+8 x -9,
13 x <13,
x <1.
9. [2024揭阳模拟]已知多项式 x -1与 x2+ ax -1的乘积中不
含 x2项,则常数 a 的值为( D )
A. 0 B.
C. -1 D. 1
D
10. [2024长沙岳麓区期中]若 P =( x -3)( x -4), Q =( x -
2)( x -5),则 P 与 Q 的大小关系是( A )
A. P > Q B. P < Q
C. P = Q D. 由 x 的取值而定
A
11. [2024广州天河区月考]有足够多张如图所示的A类、B类
正方形卡片和C类长方形卡片,若要拼出一个长为(3 a +
2 b )、宽为( a + b )的大长方形,则需要C类长方形卡片
的张数为( C )
A. 3 B. 4 C. 5 D. 6
C
12. 小明在计算一道整式乘法题:( x - m )(3 x +5),因为把
“- m ”抄成了“+ m ”,得到的结果是3 x2+11 x +
10,则 m 的值为 .
13. 已知( x2+ mx -3)(2 x + n )的展开式中不含 x 的一次项,
则 mn 的值为 .
2
6
【点拨】
( x2+ mx -3)(2 x + n )=2 x3+ nx2+2 mx2+ mnx - 6x -3 n =2 x3+( n +2 m ) x2+( mn -6) x -3 n .∵( x2+
mx -3)(2 x + n )的展开式中不含 x 的一次项,∴ mn - 6=0,∴ mn =6.
14. [2024台州月考]一些代数恒等式可以用平面几何图形的
面积来表示,例如:2 x ( x + y )=2 x2+2 xy 就可以用图
①的面积表示.
多项式乘多项式
多项式乘多项式
实质
法则
单项式乘
多项式
转化
单项式乘
单项式
转化
谢谢观看!
8.3 多项式乘多项式
第8章 整式乘法
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解多项式乘多项式的运算法则,能熟练运用法则进行多项式与多项式的乘法计算,发展运算能力.
2.在多项式与多项式乘法法则的推导过程中,体会转化思想,进一步
提升有条理地分析问题的能力与语言表达能力.
3.经历探索多项式乘多项式运算法则的过程,理解数与形的关系,知道使用符号可以进行推理运算,得到的结论具有一般性,培养抽象能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
多项式乘多项式
知1-讲
感悟新知
1
1. 多项式乘多项式的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
用字母表示为(a+b)(m+n)=am+bm+an+bn.
知1-讲
感悟新知
2. 多项式与多项式相乘的几何解释
如图8.3-1,大长方形的面积可以表示为(a+b)(c+d),也可以将大长方形的面积视为四个小长方形的面积之和,即ac+ad+bc+bd. 所以(a+b)(c+d)=ac+ad+bc+bd.
感悟新知
知1-练
计算:(1)(3x+2)(2x-3)
例 1
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=3x·2x+3x·(-3)+2·2x+2×(-3)
=6x2-9x+4x-6
=6x2-5x-6.
感悟新知
知1-练
(2)(x+2)(x2-2x+4).
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=x·x2+x·(-2x)+x·4+2·x2+2·(-2x)+2×4
=x3-2x2+4x+2x2-4x+8
=x3+8.
感悟新知
知1-练
(3)(n-1)(n+1).
解题秘方:紧扣多项式乘多项式的运算法则,用“箭头法”进行计算.
解:原式=n(n2+n-n-1)=n(n2-1)=n3-n.
感悟新知
知1-练
教你一招:用“箭头法”解多项式乘多项式的问题的方法:多项式与多项式相乘,为了做到不重不漏,可以用“箭头法”标注求解,如计算(x-2y)(5a-3b)时,可作标注: ,根据箭头指示,即可得到x·5a、x·(-3b)、(-2y)·5a、(-2y)·(-3b),把各项相加,继续求解即可.
感悟新知
知1-练
方法点拨
(x+a)(x+b)型的多项式乘法,直接用(x+a)·(x+b)=x2+(a+b)x+ab 计算更简便.
感悟新知
知1-练
另解
(2)可以将x2-2x+4 看成一个整体,利用分配律计算:(x+2)(x2-2x+4)=x(x2-2x+4)+2(x2-2x+4)=x3-2x2+4x+2x2-4x+8=x3+8.
典例 计算:
(1) ;
解:
(提示:有同类项的要合并同类项)
.
(2) ;
解:
.
(3) .
解:
1. [2024佛山顺德区期中]计算( x +5)( x -3)的结果是( C )
A. x2-15 B. x2+15
C. x2+2 x -15 D. x2-2 x -15
C
2. 观察下列两个多项式相乘的运算过程:根据你发现的规
律,若( x + a )( x + b )= x2-7 x +12,则 a , b 的值可能
分别是( A )
A. -3,-4 B. -3,4
C. 3,-4 D. 3,4
A
3. [2024沈阳沈河区期末]两个关于 x 的一次整式3 x +9与6 x
-8相乘,所得结果的一次项系数为( B )
A. 18 B. 30
C. 78 D. -72
B
4. 若(5 x -6)(2 x -3)= ax2+ bx + c ,则2 a + b - c 等于
( A )
A. -25 B. -11
C. 4 D. 11
A
5. [2024宿迁一模]若 x2-9=( x +3)( x + a ),则 a =
.
6. 已知 x + y =5, xy =-36,则( x -2)( y -2)的值为
.
-3
-42
7. [母题教材P102练习T1]计算:
(1)(-7 x2-8 y2)·(- x2+3 y2);
【解】原式=7 x4-21 x2 y2+8 x2 y2-24 y4=7 x4-13 x2
y2-24 y4.
(2)(3 x +2 y )(9 x2-6 xy +4 y2);
【解】原式=27 x3-18 x2 y +12 xy2+18 x2 y -12 xy2+
8 y3=27 x3+8 y3.
(3)(3 x -2 y )( y -3 x )-(2 x - y )(3 x + y ).
【解】原式=3 xy -9 x2-2 y2+6 xy -(6 x2+2 xy - 3 xy - y2)
=3 xy -9 x2-2 y2+6 xy -6 x2-2 xy +3 xy + y2
=10 xy -15 x2- y2.
8. 解方程或不等式:
(1)5 x ( x +2)-( x +1)( x -1)=4( x2-6);
【解】5 x ( x +2)-( x +1)( x -1)=4( x2-6),
5 x2+10 x -( x2- x + x -1)=4 x2-24,
5 x2+10 x - x2+1=4 x2-24,
10 x =-25,
x =-2.5.
(2)( x -3)( x -2)-2>( x +9)( x -1).
【解】( x -3)( x -2)-2>( x +9)( x -1),
x2-2 x -3 x +6-2> x2- x +9 x -9,
x2-5 x +4> x2+8 x -9,
13 x <13,
x <1.
9. [2024揭阳模拟]已知多项式 x -1与 x2+ ax -1的乘积中不
含 x2项,则常数 a 的值为( D )
A. 0 B.
C. -1 D. 1
D
10. [2024长沙岳麓区期中]若 P =( x -3)( x -4), Q =( x -
2)( x -5),则 P 与 Q 的大小关系是( A )
A. P > Q B. P < Q
C. P = Q D. 由 x 的取值而定
A
11. [2024广州天河区月考]有足够多张如图所示的A类、B类
正方形卡片和C类长方形卡片,若要拼出一个长为(3 a +
2 b )、宽为( a + b )的大长方形,则需要C类长方形卡片
的张数为( C )
A. 3 B. 4 C. 5 D. 6
C
12. 小明在计算一道整式乘法题:( x - m )(3 x +5),因为把
“- m ”抄成了“+ m ”,得到的结果是3 x2+11 x +
10,则 m 的值为 .
13. 已知( x2+ mx -3)(2 x + n )的展开式中不含 x 的一次项,
则 mn 的值为 .
2
6
【点拨】
( x2+ mx -3)(2 x + n )=2 x3+ nx2+2 mx2+ mnx - 6x -3 n =2 x3+( n +2 m ) x2+( mn -6) x -3 n .∵( x2+
mx -3)(2 x + n )的展开式中不含 x 的一次项,∴ mn - 6=0,∴ mn =6.
14. [2024台州月考]一些代数恒等式可以用平面几何图形的
面积来表示,例如:2 x ( x + y )=2 x2+2 xy 就可以用图
①的面积表示.
多项式乘多项式
多项式乘多项式
实质
法则
单项式乘
多项式
转化
单项式乘
单项式
转化
谢谢观看!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
