9.1 平移 课件（共31张PPT）

(共31张PPT)
9.1 平移
第9章 图形的变换
苏科版（2024）数学七年级下册
授课教师：********
班 级：********
时 间：********
学习目标
1.通过具体实例认识平移，探索它的基本性质，体会变化中的不变性，进一步发展空间观念.
2.能按照要求作出简单图形平移后的图形，发展动手操作能力、几何直观和审美意识.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念，能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性，掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析，培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程，体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动，敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性，体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性，理解原命题为真，其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
（一）导入新课（5 分钟）
展示一些简单的命题，如 “如果两个角是对顶角，那么这两个角相等” ，“如果 a=b，那么 a =b ”。引导学生分析这些命题的题设和结论。
提问：能否交换这些命题的题设和结论，得到新的命题？新命题是否成立？从而引出本节课的课题 —— 互逆命题、互逆定理。
（二）讲授新课（25 分钟）
互逆命题
给出互逆命题的定义：在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论又是第二个命题的题设，那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。
举例说明：如原命题 “如果两个角是直角，那么这两个角相等”，它的逆命题是 “如果两个角相等，那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论，每个小组写出 3 - 5 个命题，并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题，需要通过推理证明；对于假命题，只需举一个反例即可。
以刚才的命题为例，分析原命题和逆命题的真假性。如 “如果两个角是直角，那么这两个角相等” 是真命题，而它的逆命题 “如果两个角相等，那么这两个角是直角” 是假命题，因为两个相等的角不一定是直角，还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性，并在小组内交流。
互逆定理
给出互逆定理的定义：如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，这两个定理叫做互逆定理，其中一个定理叫做另一个定理的逆定理。
举例说明：如 “两直线平行，同位角相等” 和 “同位角相等，两直线平行” 是互逆定理。
强调：并不是所有的定理都有逆定理，只有当定理的逆命题为真命题时，才有逆定理。
（三）例题讲解（15 分钟）
例 1：写出下列命题的逆命题，并判断其真假。
（1）如果 a = 0，那么 ab = 0。
（2）全等三角形的对应角相等。
（3）等腰三角形的两个底角相等。
分析：
（1）逆命题为 “如果 ab = 0，那么 a = 0”，这是假命题，因为当 b = 0 时，ab = 0，a 不一定为 0。
（2）逆命题为 “对应角相等的三角形是全等三角形”，这是假命题，因为对应角相等的三角形不一定全等，可能是相似三角形。
（3）逆命题为 “有两个角相等的三角形是等腰三角形”，这是真命题，它是等腰三角形的判定定理。
例 2：证明命题 “如果一个三角形的两个角相等，那么这两个角所对的边也相等” 是真命题。
分析：引导学生画出图形，写出已知、求证，然后进行证明。
已知：在△ABC 中，∠B = ∠C。
求证：AB = AC。
证明：作∠BAC 的平分线 AD，交 BC 于点 D。
因为 AD 平分∠BAC，所以∠BAD = ∠CAD。
在△ABD 和△ACD 中，
∠B = ∠C，
∠BAD = ∠CAD，
AD = AD（公共边），
所以△ABD≌△ACD（AAS）。
所以 AB = AC。
（四）课堂练习（10 分钟）
写出下列命题的逆命题，并判断真假。
（1）如果 x = 2，那么 x = 4。
（2）直角三角形的两个锐角互余。
（3）对顶角相等。
判断下列说法是否正确：
（1）每个命题都有逆命题。
（2）每个定理都有逆定理。
（3）真命题的逆命题一定是真命题。
（4）假命题的逆命题一定是假命题。
（五）课堂小结（5 分钟）
与学生一起回顾互逆命题、互逆定理的概念，以及如何判断命题的真假。
强调：原命题为真，逆命题不一定为真；原命题为假，逆命题也不一定为假。
（六）布置作业（5 分钟）
课本课后习题，要求学生认真书写解题过程，判断命题真假时要说明理由。
拓展作业：收集生活中或数学学习中至少两个互逆命题，并分析它们的真假性。
五、教学反思
在教学过程中，要注重引导学生积极思考、主动参与，通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误，要及时给予纠正和指导。在今后的教学中，可以进一步加强练习，提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
定义 一般地，在平面内，将一个图形沿直线 的某个方向平行移动一定的距离后得到 另一个图形的平面变换叫作平移. _________________________________
把三角形
沿直线 平
移，得到三角
形 .
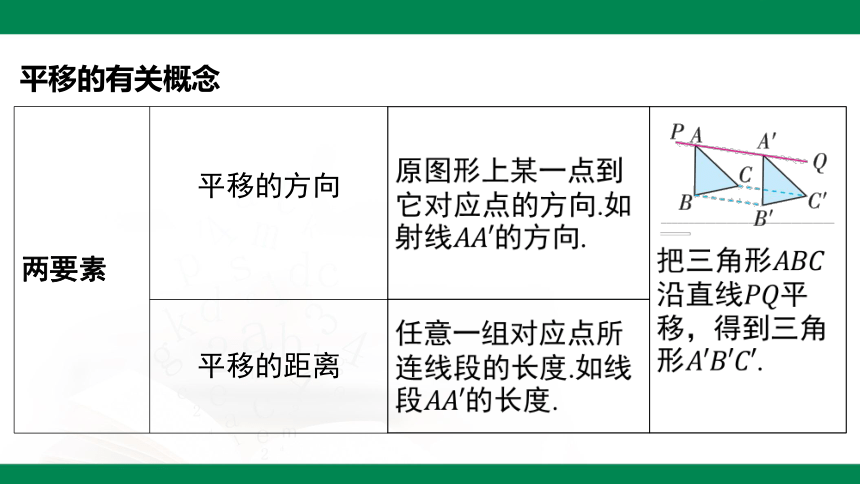
平移的有关概念
两要素 平移的方向 原图形上某一点到 它对应点的方向.如 射线 的方向. _________________________________
把三角形
沿直线 平
移，得到三角
形 .
平移的距离 任意一组对应点所 连线段的长度.如线 段 的长度.
平移的有关概念
对 应 元 素 对应 点 点与点，点与点，点与点 . _________________________________
把三角形
沿直线 平
移，得到三角
形 .
对应 线段 与，与，与 ，且 ,， .
平移的有关概念
对 应 元 素 对应 角 与，与 ， 与，且 ， ， . _________________________________
把三角形
沿直线 平
移，得到三角
形 .
平移的有关概念
由平移的定义可知，平移前后的两个图形可以重合，
对应线段相等，对应角也相等.
平移只改变图形的位置，不改变图形的形状和大小
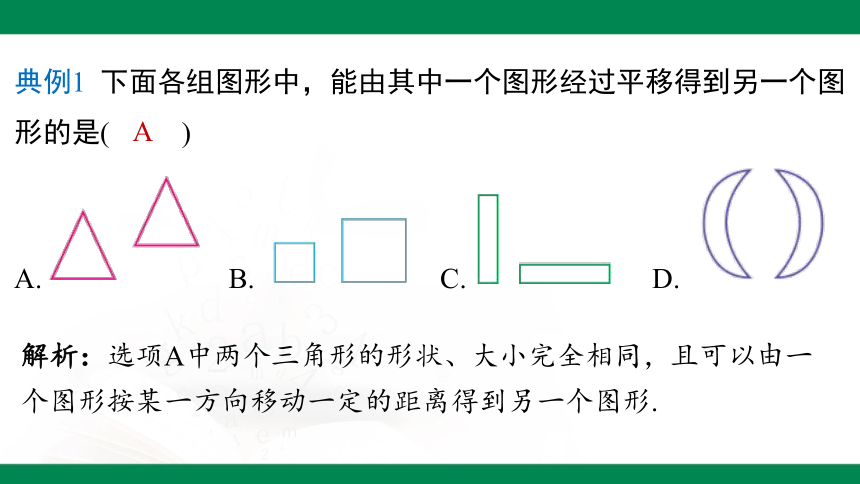
典例1 下面各组图形中，能由其中一个图形经过平移得到另一个图
形的是( )
A
A. B. C. D.
解析：选项A中两个三角形的形状、大小完全相同，且可以由一个图形按某一方向移动一定的距离得到另一个图形.
性质 符号语言 图示
平移后得到的新图形与原图形 的形状、大小完全相同. ______________________
平移的基本性质
性质 符号语言 图示
平移前后的两个图形中，两组对应点的连线段平行且相等. 如右图（1）， ， ， ， 与 在同一条直 线上. 如右图（2）, ， . ______________________
平移的基本性质
性质 符号语言 图示
拓展：平移前后两个图形中的对应线段、平行（或在同一条直线上）且相等. 如右图（2）， , , ， , ， . ______________________
平移的基本性质
典例2 如图，将面积为3的三角形 沿
方向平移到三角形的位置， ，
， ，则
（1）___， ____;
2
（2）与 的关系是_________________；
,
（3）平移的距离是___，三角形 的面积是___.
7
3
平移作图的基本步骤
典例3 如图，经过平移，四边形的顶点移动到点 .
（1）指出平移的方向和平移的距离；
解：如图，连接 .
平移的方向:点到点 的方向.
平移的距离:线段 的长度.
（2）画出平移后的四边形 .
解：如图,分别过点,,按射线的方向作线段,, ,
使得它们与线段平行且相等，连接,,, .
四边形就是四边形 平移后得到的图形.
1. [2024邯郸月考] 下列现象中，属于平移的是( )
A
A. 传送带上物品的输送 B. 教室的门打开
C. 方向盘的转动 D. 钟摆的运动
2. 甲骨文是中华优秀传统文化的根脉.下列甲
骨文中，能用其中一部分平移得到的是( )
D
A. B. C. D.
返回
（第3题）
3. [2024海阳期末] 小亮绘制了一个如图所示
的大长方形，上面绘有五个小长方形，若这
五个小长方形的周长之和为50，则大长方形
的周长为( )
B
A. 25 B. 50 C. 75 D. 100
返回
4. 如图，一块长方形草坪的长为 ，
宽为，在草坪中间，有一条处处为 宽的弯曲小路，则
这块草坪被青草覆盖的面积为____ .
12
（第4题）
返回
5. 如图，在正方形
网格中有两个三角形，把其中一个三角形先
横向平移格，再纵向平移 格，就能与另
一个三角形拼合成一个四边形，那么
的值为______.
6或8
【点拨】（1）当两斜边重合时可组成一个
长方形，此时，， ；
（2）当两直角边重合时有两种情况：①短
直角边重合时，此时， ，
；
②长直角边重合时，此时，， .
综上， 或8.
返回
6.
【实践与操作】 如图，平移三角形，使点平移到点 ，
画出平移后的三角形（点平移到点，点 平移到点
）.
【解】如图，三角形 即
为所求.
【猜想与推理】 猜想与 的数量关系与位置关系为
___________________，其依据是_______________________
__________________________________________.
,
连接平移前后图形各组对应点的线段平行（或在同一条直线上）且相等
返回
7. [2024泰州月考] 如图是一块从一个边长为
的正方形 材料中剪出的垫片，经
测量 ，则这个剪出的图形的周长是
( )
C
A. B. C. D.
【点拨】如图，把平移到 的位置，把
平移到的位置，把平移到 的位置，
易知这个剪出的图形的周长为
.
故选C.
返回
8. 某数学兴趣小组开展动手操作活动，设计了如图所示的三
种图形，现计划用铁丝按照图形制成相应的造型，所用铁丝
的长度分别为，， ，则它们的大小关系是( )
C
加
乙
丙
A. B.
C. D. 不能确定
返回
9. 小温同学在美术课上将三角形 通过平移设
计得到“一棵树”.如图，已知底边上的高 为
，沿方向向下平移到三角形
的位置，再经过相同的平移方式到三角形
B
A. B. C. D.
的位置，下方树干的长为，则树的高度 的长为
( )
返回
（第10题）
10. 如图，三角形的周长为 ，
若将三角形沿射线方向平移
后得到三角形，与相交于点 ，
连接，则三角形与三角形 的
周长和为( )
C
A. B. C. D.
返回
11.如图，已知在直角三角形中， ， ，
.将其沿边向右平移2个单位长度得到三角形 ，
则四边形 的面积为____.
14
（第11题）
返回
谢谢观看！