9.3 旋转 课件（共35张PPT）

(共35张PPT)
9.3 旋转
第9章 图形的变换
苏科版（2024）数学七年级下册
授课教师：********
班 级：********
时 间：********
学习目标
1.通过具体实例认识平面图形关于旋转中心的旋转,能指出旋转中心、
旋转方向和旋转角.
2.探索旋转的基本性质:旋转前后的两个图形中,对应点到旋转中心
的距离相等,对应点与旋转中心连线所成的角都等于旋转角，感悟
数学论证逻辑的严谨性，发展推理能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念，能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性，掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析，培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程，体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动，敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性，体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性，理解原命题为真，其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
（一）导入新课（5 分钟）
展示一些简单的命题，如 “如果两个角是对顶角，那么这两个角相等” ，“如果 a=b，那么 a =b ”。引导学生分析这些命题的题设和结论。
提问：能否交换这些命题的题设和结论，得到新的命题？新命题是否成立？从而引出本节课的课题 —— 互逆命题、互逆定理。
（二）讲授新课（25 分钟）
互逆命题
给出互逆命题的定义：在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论又是第二个命题的题设，那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。
举例说明：如原命题 “如果两个角是直角，那么这两个角相等”，它的逆命题是 “如果两个角相等，那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论，每个小组写出 3 - 5 个命题，并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题，需要通过推理证明；对于假命题，只需举一个反例即可。
以刚才的命题为例，分析原命题和逆命题的真假性。如 “如果两个角是直角，那么这两个角相等” 是真命题，而它的逆命题 “如果两个角相等，那么这两个角是直角” 是假命题，因为两个相等的角不一定是直角，还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性，并在小组内交流。
互逆定理
给出互逆定理的定义：如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，这两个定理叫做互逆定理，其中一个定理叫做另一个定理的逆定理。
举例说明：如 “两直线平行，同位角相等” 和 “同位角相等，两直线平行” 是互逆定理。
强调：并不是所有的定理都有逆定理，只有当定理的逆命题为真命题时，才有逆定理。
（三）例题讲解（15 分钟）
例 1：写出下列命题的逆命题，并判断其真假。
（1）如果 a = 0，那么 ab = 0。
（2）全等三角形的对应角相等。
（3）等腰三角形的两个底角相等。
分析：
（1）逆命题为 “如果 ab = 0，那么 a = 0”，这是假命题，因为当 b = 0 时，ab = 0，a 不一定为 0。
（2）逆命题为 “对应角相等的三角形是全等三角形”，这是假命题，因为对应角相等的三角形不一定全等，可能是相似三角形。
（3）逆命题为 “有两个角相等的三角形是等腰三角形”，这是真命题，它是等腰三角形的判定定理。
例 2：证明命题 “如果一个三角形的两个角相等，那么这两个角所对的边也相等” 是真命题。
分析：引导学生画出图形，写出已知、求证，然后进行证明。
已知：在△ABC 中，∠B = ∠C。
求证：AB = AC。
证明：作∠BAC 的平分线 AD，交 BC 于点 D。
因为 AD 平分∠BAC，所以∠BAD = ∠CAD。
在△ABD 和△ACD 中，
∠B = ∠C，
∠BAD = ∠CAD，
AD = AD（公共边），
所以△ABD≌△ACD（AAS）。
所以 AB = AC。
（四）课堂练习（10 分钟）
写出下列命题的逆命题，并判断真假。
（1）如果 x = 2，那么 x = 4。
（2）直角三角形的两个锐角互余。
（3）对顶角相等。
判断下列说法是否正确：
（1）每个命题都有逆命题。
（2）每个定理都有逆定理。
（3）真命题的逆命题一定是真命题。
（4）假命题的逆命题一定是假命题。
（五）课堂小结（5 分钟）
与学生一起回顾互逆命题、互逆定理的概念，以及如何判断命题的真假。
强调：原命题为真，逆命题不一定为真；原命题为假，逆命题也不一定为假。
（六）布置作业（5 分钟）
课本课后习题，要求学生认真书写解题过程，判断命题真假时要说明理由。
拓展作业：收集生活中或数学学习中至少两个互逆命题，并分析它们的真假性。
五、教学反思
在教学过程中，要注重引导学生积极思考、主动参与，通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误，要及时给予纠正和指导。在今后的教学中，可以进一步加强练习，提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察下列动画，说一说，生活中的这些现象有什么共同特点？
课堂导入
扇叶
摩天轮
荡秋千
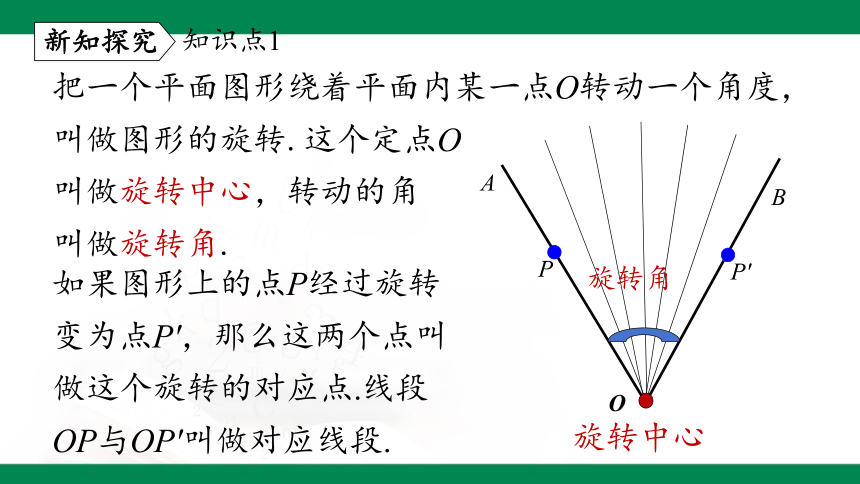
把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转.这个定点O
叫做旋转中心，转动的角
叫做旋转角.
知识点1
新知探究
旋转角
旋转中心
A
O
B
P
P′
如果图形上的点P经过旋转变为点P′，那么这两个点叫做这个旋转的对应点.线段OP与OP′叫做对应线段.
知识点1
新知探究
B
O
A
45°
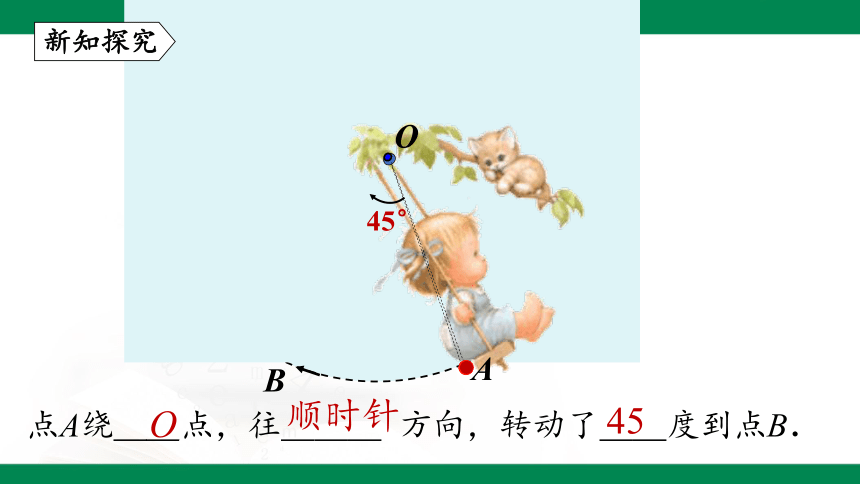
点A绕＿＿点，往＿＿＿ 方向，转动了＿＿度到点B．
O
顺时针
45
新知探究
B
A
B′
A′
C
C′
O
100 °
旋转中心
旋转角
旋转方向
旋转的三要素:
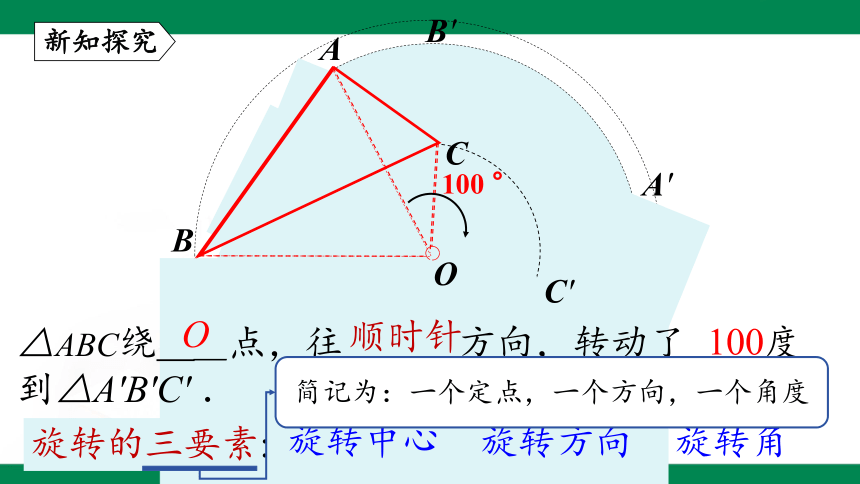
△ABC绕＿＿点，往＿＿＿方向，转动了＿＿度到△A′B′C′ ．
O
顺时针
100
简记为：一个定点，一个方向，一个角度
新知探究
①旋转变换属于全等变换.
②描述旋转时，不能忽略“平面内”,且旋转的角度一般小于360°.
③定位三要素：一个图形由一个位置旋转到另一个位置，固定不动的点就是旋转中心，互换位置的点是对应点，互换位置的边是对应边，对应边的夹角是旋转角．
例1 如图，杠杆绕支点转动撬起重物，杠杆的旋转
中心在哪里？旋转角是哪个角？
在支点O
旋转角为∠AOA′
跟踪训练
新知探究
B
O
B′
A
A′
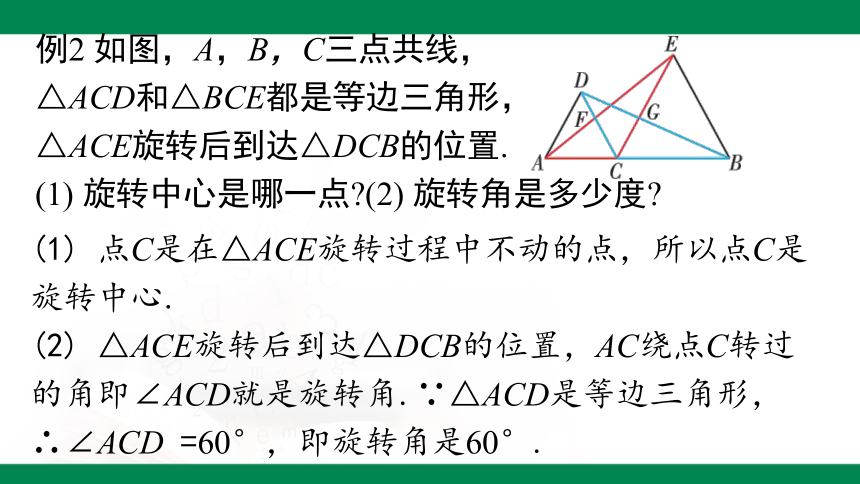
例2 如图，A，B，C三点共线，
△ACD和△BCE都是等边三角形，
△ACE旋转后到达△DCB的位置.
(1) 旋转中心是哪一点 (2) 旋转角是多少度
(1) 点C是在△ACE旋转过程中不动的点，所以点C是旋转中心.
(2) △ACE旋转后到达△DCB的位置，AC绕点C转过的角即∠ACD就是旋转角.∵△ACD是等边三角形，∴∠ACD =60°，即旋转角是60°.
知识点2
新知探究
旋转的性质
如图，在硬纸板上，挖一个三角形洞，再
另挖一个小洞O作为旋转中心，硬纸板下面
放一张白纸.先在纸上描出这个挖掉的三角
形图案（△ABC），然后围绕旋转中心转动
硬纸板，再描出这个挖掉的三角形
（△A′B′C′ ），移开硬纸板，△ A′B′C′是由
△ABC绕点O旋转得到的.
新知探究
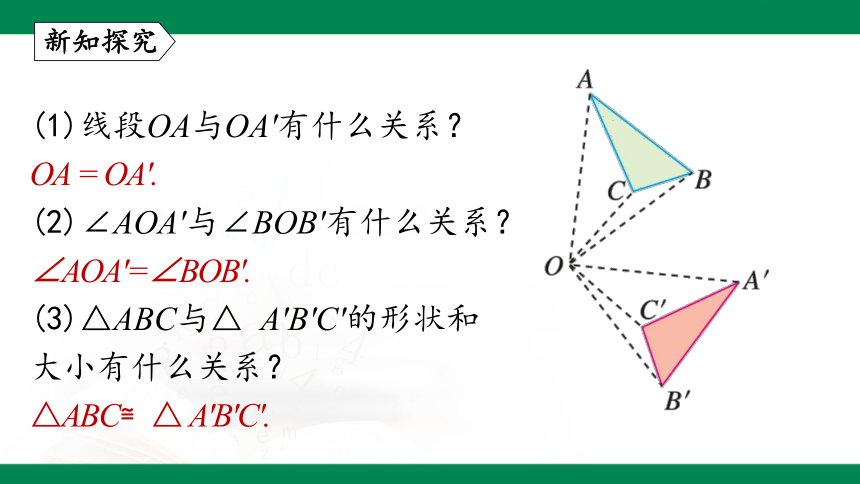
(1)线段OA与OA′有什么关系？
OA = OA′.
(2)∠AOA′与∠BOB′有什么关系？
∠AOA′=∠BOB′.
(3)△ABC与△ A′B′C′的形状和
大小有什么关系？
△ABC≌△ A′B′C′.
你能归纳出旋转的性质吗？
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
B'
A'
C'
A
B
C
O
（2）线段AO=A'O，BO=B'O，CO=C'O
（1）旋转角∠AOA'=∠BOB' =∠COC'
观察下图，你能
得到什么
结论？
（3）△ABC≌△A'B'C'
归纳总结：
(1)旋转不改变图形的形状和大小，只改变图形的位置；
(2)旋转时，图形上的每一点都绕旋转中心旋转相同的角度；
(3)旋转的性质中所说的“对应点”是指“任意一对对应点”.
例3 如图，将△ABC绕点A逆时针旋
转得到△ADE，点C和点E是对应点，
若∠CAE=90°，AB=1，则BD= .
解：将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点，所以AB=AD=1，∠BAD=∠CAE=90°，所以 BD=．
跟踪训练
新知探究
1. 如图，在边长为1的正方形网格
中，将△ABC绕点P顺时针旋转90°
得到△A′B′C′ ，则点P的坐标是( )
A.(1，1) B.(1，2)
C.(1，3) D.(1，4)
B
思路引导：
P
随堂练习
确定对应点A与A′，C与C′
作AA′，CC′的垂直平分线
两条垂直平分线的交点（1，2）即为旋转中心
旋转中心的确定：旋转中心是两对对应点所连线段的垂直平分线的交点.
2.如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB'C' 的位置，使得 CC′ //AB，则∠BAB′ 的度数是( )
A.30° B.35°
C.40° D.50°
A
解：∵CC′∥AB，∠CAB=75°，
∴∠C′CA=∠CAB=75°，
又∵C，C′ 为对应点，点 A 为旋转中心，
∴AC=AC′，即△ACC′ 为等腰三角形，
∴∠BAB′=∠CAC′=180°-2∠C′CA=30°．
本题的素养解读见《教材帮》数学RJ九上23.1节方法帮题
1. [2023德阳广汉市期中]下列现象中：①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头开关的转动；⑤钟摆的运动；⑥荡秋千运动. 属于旋转的有(　　)
A. 2个　　 B. 3个　　 C. 4个　 　D. 5个
C
返回
变式1 下列四个图形中，不能由如图所示的图形经过旋转得到的是(　　)
C
2. 如图，△AOB 绕着点O顺时针旋转至△A′OB′的位置，此时：
(1)旋转中心是________，旋转角为__________________；
(2)点B的对应点是________，
点A的对应点是________；
(3)∠A的对应角是________，
线段OB的对应线段是_________.
点O
∠AOA′(或∠BOB′)　
点B′
点A′
∠A′
线段OB′
返回
变式2如图，△ABC绕点O沿顺时针方向旋转90°到△A′B′C′的位置，则旋转中心是________，旋转角是___________________________，
∠ABC的对应角是___________，
线段AB的对应线段是_________.
点O
∠AOA′(或∠BOB′或∠COC′)
∠A′B′C′
线段A′B′
3. [2023张家界改编]如图，AO为∠BAC的平分线，且∠BAC＝50°，将四边形ABOC绕点A沿逆时针方向旋转后，得到四边形AB′O′C′，且∠OAC′＝100°，求四边形ABOC旋转的角度.
【解】
∵AO为∠BAC的平分线，∠BAC＝50°，
∴∠BAO＝∠CAO＝ ∠BAC＝25°.
由旋转的性质知∠C′AO′＝∠CAO＝25°，
旋转角为∠OAO′.
∴∠OAO′＝∠OAC′－∠C′AO′＝100°－25°＝75°，
∴四边形ABOC旋转的角度为75°.
变式3 [2023眉山三模]如图，在三角形纸片ABC中，∠C＝90°，将△ABC绕着点A按顺时针方向旋转，使得点B落在点D处，点C落在AB边上的点E处，连接BD，若AC＝4，BC＝3，求线段BD的长.
返回
返回
1. 如图，在平面内将三角形标志绕其中心旋转180°后得到的图案是(　　)
D
返回
2. [2023台州月考]如图，△ABC绕点C旋转后得到△DEC，点B旋转到点E的位置，则下列说法正确的是(　　)
A. 点B与点D是对应点　　　　　　　　　
B. ∠BCD是旋转角
C. 点A与点E是对应点　　　　　　　　　
D. △ABC≌△DEC
D
返回
3. [2023北京海淀区月考]如图，在正方形网格中，将△MNP 绕某一点旋转某一角度得到△M1N1P1，则旋转中心是(　　)
A. 点A　　　　　　　
B. 点B　　　　　　　
C. 点C　　　　　　　
D. 点D
D
4. [2023菏泽]如图，点E是正方形ABCD内的一点，将△ABE绕点B按顺时针方向旋转90°，得到△CBF，连接EF，交BC于点G. 若∠ABE＝55°，则∠EGC＝_________°.
80
【点拨】
∵四边形ABCD是正方形，∴∠ABC＝90°.
∵∠ABE＝55°，
∴∠EBC＝∠ABC－∠ABE＝35°.
由旋转得BE＝BF，∠EBF＝90°，
∴∠BEF＝∠BFE＝45°.
∵∠EGC是△BEG的一个外角，
∴∠EGC＝∠BEF＋∠EBC＝80°.
返回
5. [2023泸州模拟]如图，在矩形ABCD中，将△ADC绕点A按顺时针方向旋转得到△AFE，点F恰好落在对角线AC上，FE交BC于点P，AE交BC于点Q，∠DAC＝30°. 求证：△PQE是等边三角形.
返回
【证明】
∵四边形ABCD为矩形，
∴∠DAB＝∠D＝∠B＝90°.
由旋转的性质得∠AFE＝∠D＝90°，
∠FAE＝∠DAC＝30°，
∴∠E＝60°，∠QAB＝30°.∴∠AQB＝60°.
∴∠PQE＝∠AQB＝60°.∴△PQE是等边三角形．
旋转
定义
三要素：旋转中心，旋转方向和旋转角
性质
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转前、后的图形全等
课堂小结
谢谢观看！