10.2 二元一次方程组的概念 课件（共21张PPT）

(共21张PPT)
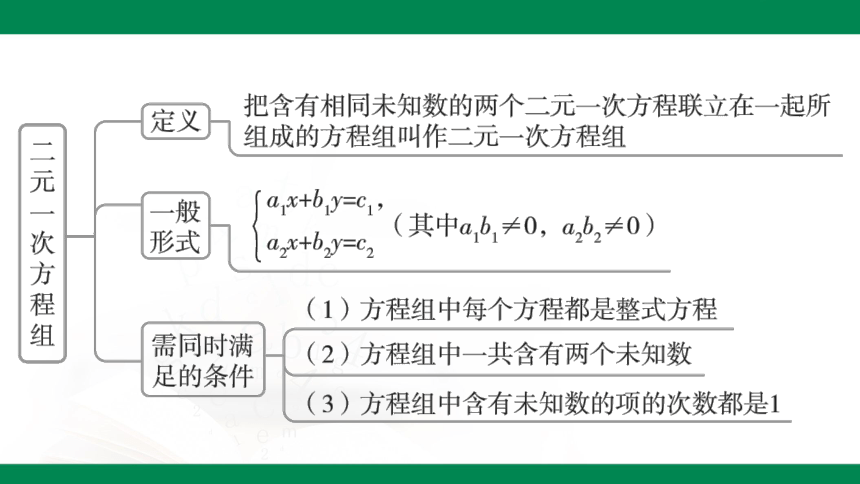
10.2 二元一次方程组的概念
第10章 二元一次方程组
苏科版（2024）数学七年级下册
授课教师：********
班 级：********
时 间：********
学习目标
1.了解二元一次方程组及二元一次方程组的解的概念，并会判断一
对数值是不是某个二元一次方程组的解，发展抽象能力.
2.能利用二元一次方程组表示实际问题中的数量关系，形成应用意
识，发展模型观念.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念，能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性，掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析，培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程，体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动，敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性，体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性，理解原命题为真，其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
（一）导入新课（5 分钟）
展示一些简单的命题，如 “如果两个角是对顶角，那么这两个角相等” ，“如果 a=b，那么 a =b ”。引导学生分析这些命题的题设和结论。
提问：能否交换这些命题的题设和结论，得到新的命题？新命题是否成立？从而引出本节课的课题 —— 互逆命题、互逆定理。
（二）讲授新课（25 分钟）
互逆命题
给出互逆命题的定义：在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论又是第二个命题的题设，那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。
举例说明：如原命题 “如果两个角是直角，那么这两个角相等”，它的逆命题是 “如果两个角相等，那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论，每个小组写出 3 - 5 个命题，并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题，需要通过推理证明；对于假命题，只需举一个反例即可。
以刚才的命题为例，分析原命题和逆命题的真假性。如 “如果两个角是直角，那么这两个角相等” 是真命题，而它的逆命题 “如果两个角相等，那么这两个角是直角” 是假命题，因为两个相等的角不一定是直角，还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性，并在小组内交流。
互逆定理
给出互逆定理的定义：如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，这两个定理叫做互逆定理，其中一个定理叫做另一个定理的逆定理。
举例说明：如 “两直线平行，同位角相等” 和 “同位角相等，两直线平行” 是互逆定理。
强调：并不是所有的定理都有逆定理，只有当定理的逆命题为真命题时，才有逆定理。
（三）例题讲解（15 分钟）
例 1：写出下列命题的逆命题，并判断其真假。
（1）如果 a = 0，那么 ab = 0。
（2）全等三角形的对应角相等。
（3）等腰三角形的两个底角相等。
分析：
（1）逆命题为 “如果 ab = 0，那么 a = 0”，这是假命题，因为当 b = 0 时，ab = 0，a 不一定为 0。
（2）逆命题为 “对应角相等的三角形是全等三角形”，这是假命题，因为对应角相等的三角形不一定全等，可能是相似三角形。
（3）逆命题为 “有两个角相等的三角形是等腰三角形”，这是真命题，它是等腰三角形的判定定理。
例 2：证明命题 “如果一个三角形的两个角相等，那么这两个角所对的边也相等” 是真命题。
分析：引导学生画出图形，写出已知、求证，然后进行证明。
已知：在△ABC 中，∠B = ∠C。
求证：AB = AC。
证明：作∠BAC 的平分线 AD，交 BC 于点 D。
因为 AD 平分∠BAC，所以∠BAD = ∠CAD。
在△ABD 和△ACD 中，
∠B = ∠C，
∠BAD = ∠CAD，
AD = AD（公共边），
所以△ABD≌△ACD（AAS）。
所以 AB = AC。
（四）课堂练习（10 分钟）
写出下列命题的逆命题，并判断真假。
（1）如果 x = 2，那么 x = 4。
（2）直角三角形的两个锐角互余。
（3）对顶角相等。
判断下列说法是否正确：
（1）每个命题都有逆命题。
（2）每个定理都有逆定理。
（3）真命题的逆命题一定是真命题。
（4）假命题的逆命题一定是假命题。
（五）课堂小结（5 分钟）
与学生一起回顾互逆命题、互逆定理的概念，以及如何判断命题的真假。
强调：原命题为真，逆命题不一定为真；原命题为假，逆命题也不一定为假。
（六）布置作业（5 分钟）
课本课后习题，要求学生认真书写解题过程，判断命题真假时要说明理由。
拓展作业：收集生活中或数学学习中至少两个互逆命题，并分析它们的真假性。
五、教学反思
在教学过程中，要注重引导学生积极思考、主动参与，通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误，要及时给予纠正和指导。在今后的教学中，可以进一步加强练习，提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
示 例 二元一次方 程组 ________________________________________________________________________________
典例1 已知,, 是未知数，下列各方程组中，是二元一次方程组
的是( )
A
A. B.
C. D.
二元一次方程组的解：我们把二元一次方程组中两个方程的公共解
叫作二元一次方程组的解.
二元一次方程组的解要用大括号联立起来，分两行书写，
如方程组的解应写成
敲黑板
二元一次方程组的解的特点
（1）方程组的解一定是方程组中每一个方程的解，但方程组中每
一个方程的解不一定是这个方程组的解.
（2）一般地，二元一次方程组的解只有一个，但也有特殊情况，
如方程组无解，方程组有无数个解.
典例2 判断下列各对数值是不是二元一次方程组 的
解.
（1）
解：(1) 把, 分别代入①和②中，可知方程①的左右两边
相等，方程②的左右两边不相等，所以 不是原方程组的解.
（2）
(2) 把, 分别代入①和②中，可知方程①的左右两边相
等，方程②的左右两边也相等，所以 是原方程组的解.
10. 已知 是二元一次方程
的一个解，则 ____.
【点拨】把代入二元一次方程 ,得
，
.
.
.
.
返回
11. 若方程组是关于，
的二元一次方程组，则代数式 的值是_________.
或
【点拨】由二元一次方程组的概念，得 ，
， ,
解得，， ,
所以 .
或，， ，
解得，，，所以 .故答案
为或 .
返回
12.两个两位数的差是20，在较大的两位数的右边接着写较小
的两位数，得到一个四位数；在较大的两位数的左边接着写
较小的两位数，也得到一个四位数，若这两个四位数的和是
，求这两个两位数分别是多少？设较大的两位数为 ，
较小的两位数为 ，根据题意可列方程组为
_ _______________________________.
返回
13.我们知道方程 有无数组解，但在实际生活中
我们往往只需要求出其正整数解.
例：由，得（， 为正整
数）.又为正整数，为3的倍数. 易得 .
代入可得 .
的正整数解为
问题：
（1）若为自然数，则满足条件的整数 的值有_________个；
4
（2）请你写出方程 的所有正整数解.
【解】由得，当时，；
当 时， ，
方程的所有正整数解为
返回
14.小明是一名爱动脑筋的同学，他经常利用课余时间钻研一
些数学问题.有一次，他发现：对于任意有理数 ,
都是方程 的解.你认为小明发现
的结论正确吗？请说明理由.
【解】小明发现的结论正确.理由:把 代入方程
的左边,得 .而方
程的右边,所以左边 右边,即小明发现的结论正确.
返回
15. 甲、乙两人共同解关于, 的方程组
解完以后有下面一段对话（如图），请认
真阅读对话内容，然后求出 的值.
【解】把代入②,得 ,
解得 .
把代入①，得 ,
解得 .
所以 .
返回
谢谢观看！