11.5 用一元一次不等式解决问题 课件(共21张PPT)
文档属性
| 名称 | 11.5 用一元一次不等式解决问题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
11.5 用一元一次不等式解决问题
第11章 一元一次不等式
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.能从实际问题中依据不等关系抽象出不等式来解决问题,培养提炼信息的能力.
2.掌握应用一元一次不等式解决实际问题的方法和步骤,发展应用意识.
3.经历“问题情境——建立数学模型——解释、应用、拓展”的过程,发展模型观念.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
有些实际问题中存在不等关系,用不等式来表示不等关系,就能把实
际问题转化为数学问题,从而通过解不等式解决实际问题.
应用一元一次不等式解决实际问题的步骤与列一元一次方程解决实
际问题的步骤类似,即:
步骤 注意事项
审 认真审题,找出已知量和未 知量,并找出它们之间的不 等关系. 抓住题目中的关键字眼,如“大于”
“小于”“不小于”“至少”“超过”等.
设 设出适当的未知数. 表示不等关系的文字如“至少”“最
多”等不能出现.
. .
. .
步骤 注意事项
列 根据题中的不等关系列出 不等式. 两边所表示的量应该相同,并且单
位要统一.
解 解不等式,求出其解集. 不等号方向及符号等不要出错.
验 检验所求出的不等式的解 集是否符合题意. 一满足不等式;二符合实际意义.
答 写出答案. 应把表示不等关系的文字补上.
典例1 (2024·山西中考)为加强校园消防安全,
学校计划购买某种型号的水基灭火器和干粉灭
火器共50个,如图,其中水基灭火器的价格为
540元/个,干粉灭火器的价格为380元/个.若
学校购买这两种灭火器的总价不超过21 000元,
则最多可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器个,
则购买干粉灭火器 个.
根据题意,得,解得 .
因为为整数,所以 的最大值为12.
答:最多可购买这种型号的水基灭火器12个.
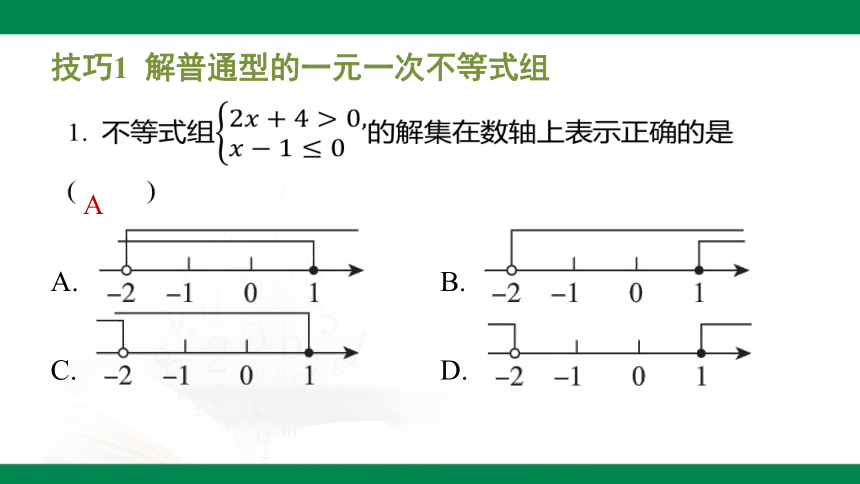
技巧1 解普通型的一元一次不等式组
1. 不等式组 的解集在数轴上表示正确的是
( )
A
A. B.
C. D.
【点拨】解,得 ,
解,得 ,
所以不等式组的解集为 .
返回
2.解不等式组 并将解集在数轴上表示出来.
【解】
解不等式①,得,解不等式②,得 ,
不等式组的解集为 .
将解集表示在数轴上如图所示.
返回
3.解不等式组 并写出满足不等式组的所有整数解.
【解】解不等式,得 ,
解不等式,得 ,
不等式组的解集为 .
不等式组的所有整数解为 ,0.
返回
技巧2 解连写型的不等式组
4. 满足不等式组 的整数解有( )
B
A. 5个 B. 4个 C. 3个 D. 无数个
5.若,且,则 的取值范围为_ _________.
【点拨】由,得 ,
根据可知 ,
解得 .
返回
6.解不等式组 .
【解】原不等式组可化为
解不等式①,得 ,
解不等式②,得 .
原不等式组的解集为 .
返回
技巧3 “绝对值”型不等式转化为不等式组求解
7.解不等式 .
【解】由 ,
得,则
解不等式①,得,解不等式②,得 .
原不等式的解集为 .
【点拨】解题时要先将含绝对值的不等式转化为不等式组再
进行求解.
返回
技巧4 “分式”型不等式转化为不等式组求解
8.解不等式 .
【解】,与 异号.
即或
解①,得 此不等式组无解.
解②,得
此不等式组的解集为 .
原不等式的解集为 .
返回
谢谢观看!
11.5 用一元一次不等式解决问题
第11章 一元一次不等式
苏科版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.能从实际问题中依据不等关系抽象出不等式来解决问题,培养提炼信息的能力.
2.掌握应用一元一次不等式解决实际问题的方法和步骤,发展应用意识.
3.经历“问题情境——建立数学模型——解释、应用、拓展”的过程,发展模型观念.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
有些实际问题中存在不等关系,用不等式来表示不等关系,就能把实
际问题转化为数学问题,从而通过解不等式解决实际问题.
应用一元一次不等式解决实际问题的步骤与列一元一次方程解决实
际问题的步骤类似,即:
步骤 注意事项
审 认真审题,找出已知量和未 知量,并找出它们之间的不 等关系. 抓住题目中的关键字眼,如“大于”
“小于”“不小于”“至少”“超过”等.
设 设出适当的未知数. 表示不等关系的文字如“至少”“最
多”等不能出现.
. .
. .
步骤 注意事项
列 根据题中的不等关系列出 不等式. 两边所表示的量应该相同,并且单
位要统一.
解 解不等式,求出其解集. 不等号方向及符号等不要出错.
验 检验所求出的不等式的解 集是否符合题意. 一满足不等式;二符合实际意义.
答 写出答案. 应把表示不等关系的文字补上.
典例1 (2024·山西中考)为加强校园消防安全,
学校计划购买某种型号的水基灭火器和干粉灭
火器共50个,如图,其中水基灭火器的价格为
540元/个,干粉灭火器的价格为380元/个.若
学校购买这两种灭火器的总价不超过21 000元,
则最多可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器个,
则购买干粉灭火器 个.
根据题意,得,解得 .
因为为整数,所以 的最大值为12.
答:最多可购买这种型号的水基灭火器12个.
技巧1 解普通型的一元一次不等式组
1. 不等式组 的解集在数轴上表示正确的是
( )
A
A. B.
C. D.
【点拨】解,得 ,
解,得 ,
所以不等式组的解集为 .
返回
2.解不等式组 并将解集在数轴上表示出来.
【解】
解不等式①,得,解不等式②,得 ,
不等式组的解集为 .
将解集表示在数轴上如图所示.
返回
3.解不等式组 并写出满足不等式组的所有整数解.
【解】解不等式,得 ,
解不等式,得 ,
不等式组的解集为 .
不等式组的所有整数解为 ,0.
返回
技巧2 解连写型的不等式组
4. 满足不等式组 的整数解有( )
B
A. 5个 B. 4个 C. 3个 D. 无数个
5.若,且,则 的取值范围为_ _________.
【点拨】由,得 ,
根据可知 ,
解得 .
返回
6.解不等式组 .
【解】原不等式组可化为
解不等式①,得 ,
解不等式②,得 .
原不等式组的解集为 .
返回
技巧3 “绝对值”型不等式转化为不等式组求解
7.解不等式 .
【解】由 ,
得,则
解不等式①,得,解不等式②,得 .
原不等式的解集为 .
【点拨】解题时要先将含绝对值的不等式转化为不等式组再
进行求解.
返回
技巧4 “分式”型不等式转化为不等式组求解
8.解不等式 .
【解】,与 异号.
即或
解①,得 此不等式组无解.
解②,得
此不等式组的解集为 .
原不等式的解集为 .
返回
谢谢观看!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
