江苏省宿迁市沭阳县外国语实验学校2024-2025学年八年级下学期3月月考数学试题(无答案)
文档属性
| 名称 | 江苏省宿迁市沭阳县外国语实验学校2024-2025学年八年级下学期3月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 10:06:43 | ||
图片预览


文档简介
2024~2025 学年度第二学期第一次定时作业
初二年级数学
(考试时间:120 分钟 试卷分值:150 分 )
一、选择题(本大题共 8 小题。每小题 3 分,共 24 分。在每小题给出的四个选项中只有一个符合题目要求的,
请将答案序号填在答题卡相应的位置上)
1.下列调查中,最适合采用抽样调查的是 ( )
A.调查本班同学对沭阳县总面积的知晓情况 B.调查神舟十九号载人飞船发射前各零部件的质量
C.调查 2024 年国庆期间来宿迁旅游的游客满意度 D.审查某篇文章中的错别字
2.如图,电路图上有 4 个开关 A、B、C、D 和 1 个小灯泡,同时闭合开关 A、B 或同时闭合开关 C、D 都可以使
小灯泡发光.下列操作中, “小灯泡发光”这个事件是随机事件的是( )
A.只闭合 1 个开关 B.只闭合 2 个开关
C.只闭合 3 个开关 D.闭合 4 个开关
3. 下列 条 件 不 能 识 别 一 个 四 边 形 是 平 行 四 边 形 的 是( )
A.一组对边平行且相等 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行,另一组对边相等
4.下列命题错误的是 ( )
A.平行四边形的对边相等 B.两组对边分别相等的四边形是平行四边形
C.对角线相等的四边形是矩形 D.矩形的对角线相等
5.随着智能手机的普及, “支付宝支付”和“微信支付”等手机支付方式
备受广大消费者的青睐,枣庄购物中心对 2021 年 7-12 月中使用这两种支付
方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出
以下四个推断,其中不合理的是( )
A.6 个月中 11 月份使用手机支付的总次数最多
B.6 个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多
C.6 个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大
D.9 月份平均每天使用手机支付的次数为 0.314 万次
6、如图: 在 ABCD 中, AE⊥BC 于 E, AF⊥CD 于 F。若 AE=4, AF=6, 且 ABCD 的周长为 40, 则 ABCD 的面积
为 ( )
A. 24 'B. 36 C. 40 D. 48
7、在四边形 ABCD 中, 从①AB∥CD; ②AB=CD; ③BC∥AD; ④BC=AD 中任选两个使四边形 ABOD 为平行四边形
的选法有( )
A. 3 B. 4 C. 5 D. 6
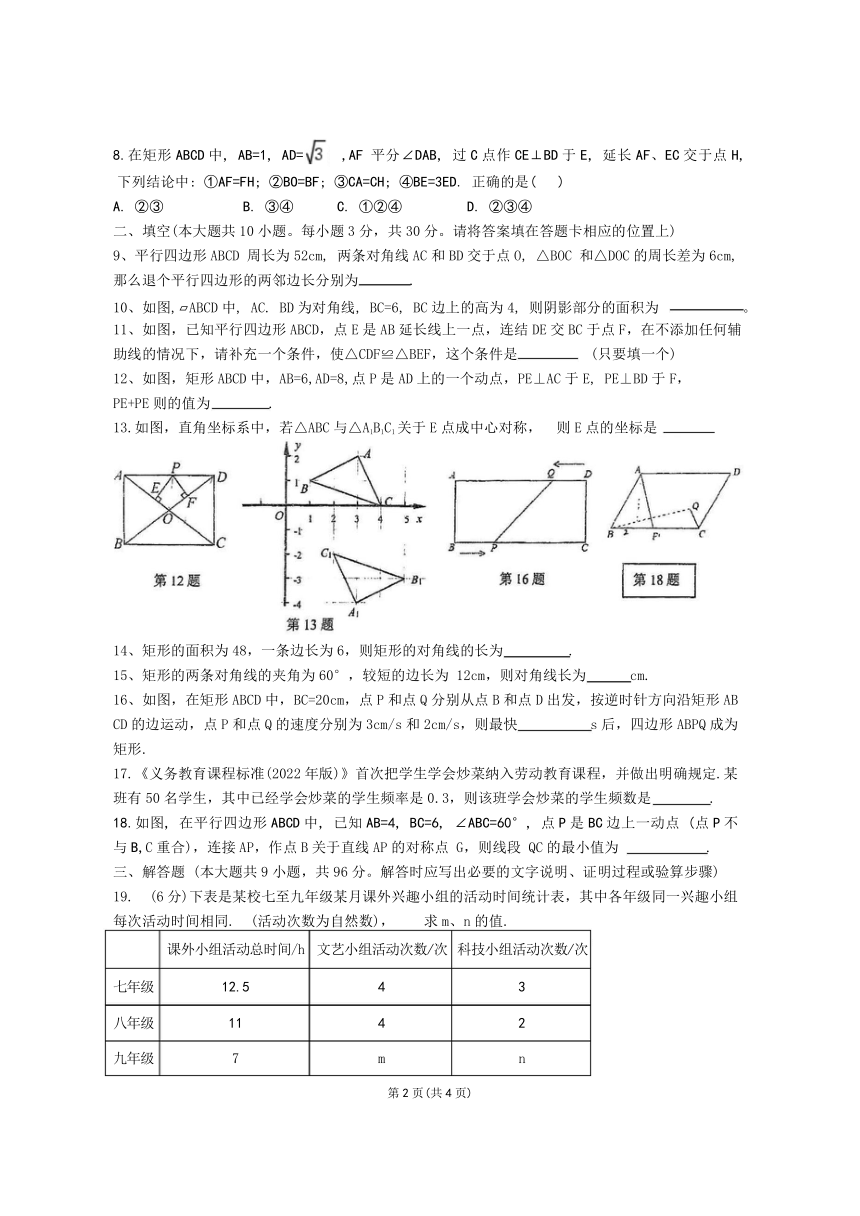
8.在矩形 ABCD 中, AB=1, AD= ,AF 平分∠DAB, 过 C 点作 CE⊥BD 于 E, 延长 AF、EC 交于点 H,
下列结论中: ①AF=FH; ②BO=BF; ③CA=CH; ④BE=3ED. 正确的是( )
A. ②③ B. ③④ C. ①②④ D. ②③④
二、填空(本大题共 10 小题。每小题 3 分,共 30 分。请将答案填在答题卡相应的位置上)
9、平行四边形 ABCD 周长为 52cm, 两条对角线 AC 和 BD 交于点 O, △BOC 和△DOC 的周长差为 6cm,
那么退个平行四边形的两邻边长分别为 .
10、如图, ABCD 中, AC. BD 为对角线, BC=6, BC 边上的高为 4, 则阴影部分的面积为 。
11、如图,已知平行四边形 ABCD,点 E 是 AB 延长线上一点,连结 DE 交 BC 于点 F,在不添加任何辅
助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是 (只要填一个)
12、如图,矩形 ABCD 中,AB=6,AD=8,点 P 是 AD 上的一个动点,PE⊥AC 于 E, PE⊥BD 于 F,
PE+PE 则的值为 .
13.如图,直角坐标系中,若△ABC 与△A1B1C1 关于 E 点成中心对称, 则 E 点的坐标是
14、矩形的面积为 48,一条边长为 6,则矩形的对角线的长为 .
15、矩形的两条对角线的夹角为 60°,较短的边长为 12cm,则对角线长为 cm.
16、如图,在矩形 ABCD 中,BC=20cm,点 P 和点 Q 分别从点 B 和点 D 出发,按逆时针方向沿矩形 AB
CD 的边运动,点 P 和点 Q 的速度分别为 3cm/s 和 2cm/s,则最快 s 后,四边形 ABPQ 成为
矩形.
17.《义务教育课程标准(2022 年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某
班有 50 名学生,其中已经学会炒菜的学生频率是 0.3,则该班学会炒菜的学生频数是 .
18.如图, 在平行四边形 ABCD 中, 已知 AB=4, BC=6, ∠ABC=60°, 点 P 是 BC 边上一动点 (点 P 不
与 B,C 重合),连接 AP,作点 B 关于直线 AP 的对称点 G,则线段 QC 的最小值为 .
三、解答题 (本大题共 9 小题,共 96 分。解答时应写出必要的文字说明、证明过程或验算步骤)
19. (6 分)下表是某校七至九年级某月课外兴趣小组的活动时间统计表,其中各年级同一兴趣小组
每次活动时间相同. (活动次数为自然数), 求 m、n 的值.
课外小组活动总时间/h 文艺小组活动次数/次 科技小组活动次数/次
七年级 12.5 4 3
八年级 11 4 2
九年级 7 m n
第 2 页(共 4 页)
20.(8 分)某校体育组为了解全校学生“最喜欢的一项球类项
目”,随机抽取了部分学生进行调查,下面是根据调查结果
绘制的不完整的统计图.则由统计图可知,在扇形统计图中,
补全条形统计图并求“乒乓球”部分所对应的圆心角的度数.
21. (9 分)如图,在平面直角坐标系中,已知△ABC 的三个顶
点的坐标分别为 A (-4, 1) , B (-1, -1),C (-3, 2)
(1) △A1B1C1 与△ABC 关于原点 O 成中心对称,画出△A1B1C1
(2)将△ABC 绕点 B 顺时针旋转 90°得到△A2B2C2,画出△A2B2C2
(3) 求△ABC 的面积.
22.(8 分)某课外学习小组做摸球试验:一只不透明的袋子中装
有若干个红球和白球,这些球除颜色外都相同.将这个袋中的球
搅匀后从中任意摸出 1 个球,记下颜色后放回、搅匀,不断重
复这个过程,获得如下数据;
摸球个数 200 300 400 500 1000 1600 2000
摸到白球的个数 116 192 232 _ 590 968 1202
摸到白球的频率 0.580 0.640 0.580 0.596 0.590 0.605 ______
(1)填写表中的空格;
(2)当摸球次数很大时,摸到白球的概率的估计值是 (精确到 0.01);
(3)若袋中有红球 2 个,请估计袋中白球的个数。
23. (8 分) 如图, 已知 ABCD 中, E、F 是对角线 BD 上的两点, BE=DF,
点 G、H 分别在 BA 和 DC 的延长线上, 且 AG=CH, 连接 GE、EH、HF、FG.
说明: 四边形 GEHF 是平行四边形.
24.(9 分)同学们要善于用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.
(1)观察发现
为了解某种小麦的发芽率,小明团队进行了试验,他们在相同条件下进行发芽试验,结果如下表:
试验
的麦 100 200 500 1000 2000 5000
粒数 n
发芽
的麦 94 191 473 954 1906 4748
粒数 m
发芽的
频率 m
第 3 页(共 4 页)
①当试验的麦粒数位 5000 时, 发芽的频率为 0.9496,0.9496 是小麦发芽的概率吗 )
A. 是 B.不是
②当任取一粒麦粒,估计它能发芽的概率是 (结果精确到 0.01)
(2)迁移应用
如图,学校操场旁的地面上铺满了正方形的地砖 40×40cm, 现在向这一地面上抛掷半径为
5cm 的圆碟,圆碟与地砖间的缝隙相交的概率是 .(直接写出答案)[
25、 (8 分) 如图, 在矩形 ABCD 中, 点 E 在 BC 上, AE=AD, DF⊥AE 于 F,连
接 DE. 求证: DF=DC.
26、(12 分)如图,四边形 ABCD 中,对角线 AC、BD 相交于点 O,AC=OO,EO=DO 中,且∠ABC+∠ADC=180°.
(1)求证:四边形 ABCD 是矩形.
(2) 若∠ADF: ∠FDC=3: 2, DF⊥AC, 则∠BDF 的度数是多少
27. (12 分)如图 ,将一块长方形纸板摆放在平面直角坐标系中,使长方形纸版的一个直角顶点 与坐标原
点重合,两条边与坐标轴重合,已知 BC=4,AB=3. (1)求直线 AC 的解析式;
(2)将长方形纸板的一个直角沿 AE 折叠,使 B 点恰好落在线
段 AC 上的 B’处,折痕 AE 交 BC 边于点 E(图 2),求点坐标;
(3)在(2)的条件下,直线 AC 上是否存在一点 P,使得 S△ADP=
S△ABE 若存在,请直接写出点 P 的坐标,若不存在,请简要说
明理由.
28。 (14 分)已知:等边三角形 ABC 的边长为 4 厘米,长为 1 厘米的线段 MN 在△ABC 的边 AB 上沿 AB 方向
以 1 厘米/秒的速度向 B 点运动(运动开始时,点 M 与点 A 重合,点 N 到达点 B 时运动终止),过点 M、N 分
别作 AB 边的垂线,与△ABC 的其它边交于 P、Q 两点,线段 MN 运动的时间为 t 秒.
(1)线段 MN 在运动的过程中,t 为何值时,四边形 MNQP 为矩形并求出该矩形的面积;
(2)线段 MN 在运动的过程中,四边形 MNQP 的面积为 S,运动的时间为 t,求四边
形 MNQP 的面积 S 随运动时间 t 变化的关系式,并写出对应的 t 的取值范围.
第 4 页(共 4 页)
初二年级数学
(考试时间:120 分钟 试卷分值:150 分 )
一、选择题(本大题共 8 小题。每小题 3 分,共 24 分。在每小题给出的四个选项中只有一个符合题目要求的,
请将答案序号填在答题卡相应的位置上)
1.下列调查中,最适合采用抽样调查的是 ( )
A.调查本班同学对沭阳县总面积的知晓情况 B.调查神舟十九号载人飞船发射前各零部件的质量
C.调查 2024 年国庆期间来宿迁旅游的游客满意度 D.审查某篇文章中的错别字
2.如图,电路图上有 4 个开关 A、B、C、D 和 1 个小灯泡,同时闭合开关 A、B 或同时闭合开关 C、D 都可以使
小灯泡发光.下列操作中, “小灯泡发光”这个事件是随机事件的是( )
A.只闭合 1 个开关 B.只闭合 2 个开关
C.只闭合 3 个开关 D.闭合 4 个开关
3. 下列 条 件 不 能 识 别 一 个 四 边 形 是 平 行 四 边 形 的 是( )
A.一组对边平行且相等 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行,另一组对边相等
4.下列命题错误的是 ( )
A.平行四边形的对边相等 B.两组对边分别相等的四边形是平行四边形
C.对角线相等的四边形是矩形 D.矩形的对角线相等
5.随着智能手机的普及, “支付宝支付”和“微信支付”等手机支付方式
备受广大消费者的青睐,枣庄购物中心对 2021 年 7-12 月中使用这两种支付
方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出
以下四个推断,其中不合理的是( )
A.6 个月中 11 月份使用手机支付的总次数最多
B.6 个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多
C.6 个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大
D.9 月份平均每天使用手机支付的次数为 0.314 万次
6、如图: 在 ABCD 中, AE⊥BC 于 E, AF⊥CD 于 F。若 AE=4, AF=6, 且 ABCD 的周长为 40, 则 ABCD 的面积
为 ( )
A. 24 'B. 36 C. 40 D. 48
7、在四边形 ABCD 中, 从①AB∥CD; ②AB=CD; ③BC∥AD; ④BC=AD 中任选两个使四边形 ABOD 为平行四边形
的选法有( )
A. 3 B. 4 C. 5 D. 6
8.在矩形 ABCD 中, AB=1, AD= ,AF 平分∠DAB, 过 C 点作 CE⊥BD 于 E, 延长 AF、EC 交于点 H,
下列结论中: ①AF=FH; ②BO=BF; ③CA=CH; ④BE=3ED. 正确的是( )
A. ②③ B. ③④ C. ①②④ D. ②③④
二、填空(本大题共 10 小题。每小题 3 分,共 30 分。请将答案填在答题卡相应的位置上)
9、平行四边形 ABCD 周长为 52cm, 两条对角线 AC 和 BD 交于点 O, △BOC 和△DOC 的周长差为 6cm,
那么退个平行四边形的两邻边长分别为 .
10、如图, ABCD 中, AC. BD 为对角线, BC=6, BC 边上的高为 4, 则阴影部分的面积为 。
11、如图,已知平行四边形 ABCD,点 E 是 AB 延长线上一点,连结 DE 交 BC 于点 F,在不添加任何辅
助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是 (只要填一个)
12、如图,矩形 ABCD 中,AB=6,AD=8,点 P 是 AD 上的一个动点,PE⊥AC 于 E, PE⊥BD 于 F,
PE+PE 则的值为 .
13.如图,直角坐标系中,若△ABC 与△A1B1C1 关于 E 点成中心对称, 则 E 点的坐标是
14、矩形的面积为 48,一条边长为 6,则矩形的对角线的长为 .
15、矩形的两条对角线的夹角为 60°,较短的边长为 12cm,则对角线长为 cm.
16、如图,在矩形 ABCD 中,BC=20cm,点 P 和点 Q 分别从点 B 和点 D 出发,按逆时针方向沿矩形 AB
CD 的边运动,点 P 和点 Q 的速度分别为 3cm/s 和 2cm/s,则最快 s 后,四边形 ABPQ 成为
矩形.
17.《义务教育课程标准(2022 年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某
班有 50 名学生,其中已经学会炒菜的学生频率是 0.3,则该班学会炒菜的学生频数是 .
18.如图, 在平行四边形 ABCD 中, 已知 AB=4, BC=6, ∠ABC=60°, 点 P 是 BC 边上一动点 (点 P 不
与 B,C 重合),连接 AP,作点 B 关于直线 AP 的对称点 G,则线段 QC 的最小值为 .
三、解答题 (本大题共 9 小题,共 96 分。解答时应写出必要的文字说明、证明过程或验算步骤)
19. (6 分)下表是某校七至九年级某月课外兴趣小组的活动时间统计表,其中各年级同一兴趣小组
每次活动时间相同. (活动次数为自然数), 求 m、n 的值.
课外小组活动总时间/h 文艺小组活动次数/次 科技小组活动次数/次
七年级 12.5 4 3
八年级 11 4 2
九年级 7 m n
第 2 页(共 4 页)
20.(8 分)某校体育组为了解全校学生“最喜欢的一项球类项
目”,随机抽取了部分学生进行调查,下面是根据调查结果
绘制的不完整的统计图.则由统计图可知,在扇形统计图中,
补全条形统计图并求“乒乓球”部分所对应的圆心角的度数.
21. (9 分)如图,在平面直角坐标系中,已知△ABC 的三个顶
点的坐标分别为 A (-4, 1) , B (-1, -1),C (-3, 2)
(1) △A1B1C1 与△ABC 关于原点 O 成中心对称,画出△A1B1C1
(2)将△ABC 绕点 B 顺时针旋转 90°得到△A2B2C2,画出△A2B2C2
(3) 求△ABC 的面积.
22.(8 分)某课外学习小组做摸球试验:一只不透明的袋子中装
有若干个红球和白球,这些球除颜色外都相同.将这个袋中的球
搅匀后从中任意摸出 1 个球,记下颜色后放回、搅匀,不断重
复这个过程,获得如下数据;
摸球个数 200 300 400 500 1000 1600 2000
摸到白球的个数 116 192 232 _ 590 968 1202
摸到白球的频率 0.580 0.640 0.580 0.596 0.590 0.605 ______
(1)填写表中的空格;
(2)当摸球次数很大时,摸到白球的概率的估计值是 (精确到 0.01);
(3)若袋中有红球 2 个,请估计袋中白球的个数。
23. (8 分) 如图, 已知 ABCD 中, E、F 是对角线 BD 上的两点, BE=DF,
点 G、H 分别在 BA 和 DC 的延长线上, 且 AG=CH, 连接 GE、EH、HF、FG.
说明: 四边形 GEHF 是平行四边形.
24.(9 分)同学们要善于用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.
(1)观察发现
为了解某种小麦的发芽率,小明团队进行了试验,他们在相同条件下进行发芽试验,结果如下表:
试验
的麦 100 200 500 1000 2000 5000
粒数 n
发芽
的麦 94 191 473 954 1906 4748
粒数 m
发芽的
频率 m
第 3 页(共 4 页)
①当试验的麦粒数位 5000 时, 发芽的频率为 0.9496,0.9496 是小麦发芽的概率吗 )
A. 是 B.不是
②当任取一粒麦粒,估计它能发芽的概率是 (结果精确到 0.01)
(2)迁移应用
如图,学校操场旁的地面上铺满了正方形的地砖 40×40cm, 现在向这一地面上抛掷半径为
5cm 的圆碟,圆碟与地砖间的缝隙相交的概率是 .(直接写出答案)[
25、 (8 分) 如图, 在矩形 ABCD 中, 点 E 在 BC 上, AE=AD, DF⊥AE 于 F,连
接 DE. 求证: DF=DC.
26、(12 分)如图,四边形 ABCD 中,对角线 AC、BD 相交于点 O,AC=OO,EO=DO 中,且∠ABC+∠ADC=180°.
(1)求证:四边形 ABCD 是矩形.
(2) 若∠ADF: ∠FDC=3: 2, DF⊥AC, 则∠BDF 的度数是多少
27. (12 分)如图 ,将一块长方形纸板摆放在平面直角坐标系中,使长方形纸版的一个直角顶点 与坐标原
点重合,两条边与坐标轴重合,已知 BC=4,AB=3. (1)求直线 AC 的解析式;
(2)将长方形纸板的一个直角沿 AE 折叠,使 B 点恰好落在线
段 AC 上的 B’处,折痕 AE 交 BC 边于点 E(图 2),求点坐标;
(3)在(2)的条件下,直线 AC 上是否存在一点 P,使得 S△ADP=
S△ABE 若存在,请直接写出点 P 的坐标,若不存在,请简要说
明理由.
28。 (14 分)已知:等边三角形 ABC 的边长为 4 厘米,长为 1 厘米的线段 MN 在△ABC 的边 AB 上沿 AB 方向
以 1 厘米/秒的速度向 B 点运动(运动开始时,点 M 与点 A 重合,点 N 到达点 B 时运动终止),过点 M、N 分
别作 AB 边的垂线,与△ABC 的其它边交于 P、Q 两点,线段 MN 运动的时间为 t 秒.
(1)线段 MN 在运动的过程中,t 为何值时,四边形 MNQP 为矩形并求出该矩形的面积;
(2)线段 MN 在运动的过程中,四边形 MNQP 的面积为 S,运动的时间为 t,求四边
形 MNQP 的面积 S 随运动时间 t 变化的关系式,并写出对应的 t 的取值范围.
第 4 页(共 4 页)
同课章节目录
