湖南省衡阳市逸夫中学2016届九年级下学期期中考试数学试题(附答案)
文档属性
| 名称 | 湖南省衡阳市逸夫中学2016届九年级下学期期中考试数学试题(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
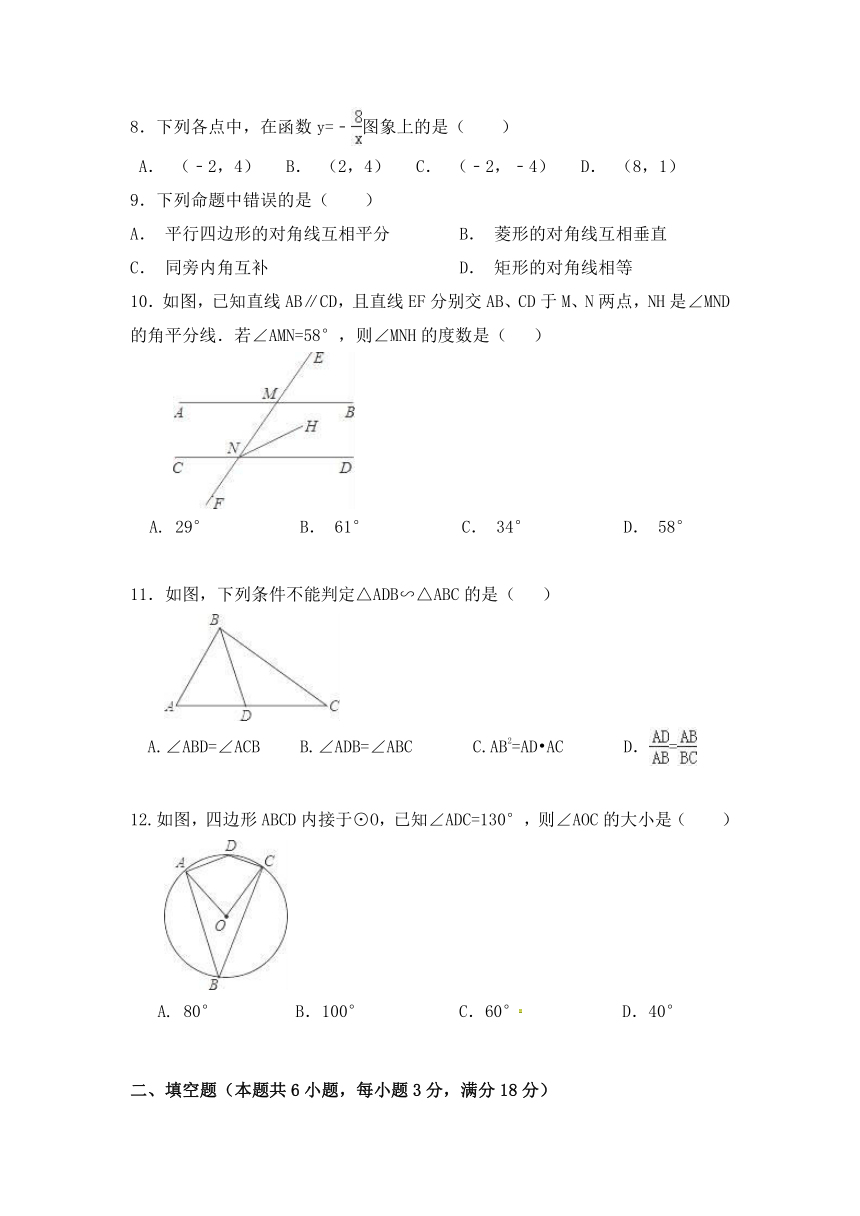
| 更新时间 | 2016-05-13 00:00:00 | ||
图片预览



文档简介
2016年上九年级数学期中考试试题
考生注意:1.本卷共26个题,共120分
2.考试时间为120分钟
一、选择题(本题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.2015的倒数为( )
A. ﹣2015 B. 2015 C. ﹣ D.
2.在数轴上表示﹣3的点与表示3的点之间的距离是( )
A. 6 B. ﹣6 C. 0 D.﹣1
3.下列运算正确的是( )
A. a6÷a3=a2 B. 5a2﹣3a2=2a C. (a3)3=a9 D. (a﹣b)2=a2﹣b2
4、已知∠α=37°,那么∠α的余角等于( )
A、37° B、53° C、63° D、143°
5.下列事件是必然事件的是( )
A. 地球绕着太阳转 B. 抛一枚硬币,正面朝上
C. 明天会下雨 D. 打开电视,正在播放新闻
6.一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
A. k>0,b>0 B. k<0,b<0 C. k<0,b>0 D. k>0,b<0
7.设x1,x2是方程x2+5x﹣3=0的两个根,则x12+x22的值是( )
A. 19 B. 25 C. 31 D. 30
8.下列各点中,在函数y=﹣图象上的是( )
A. (﹣2,4) B. (2,4) C. (﹣2,﹣4) D. (8,1)
9.下列命题中错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
10.如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=58°,则∠MNH的度数是( )
A. 29° B. 61° C. 34° D. 58°
11.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D.=
12.如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
A. 80° B.100° C.60° D.40°
二、填空题(本题共6小题,每小题3分,满分18分)
13.计算:33﹣(﹣3)= .
14. 多项式a2﹣4因式分解的结果是 .
15.在平面直角坐标系中,点(-3,2)关于轴的对称点的坐标是 .
16. 从﹣1、0、、0.3、π、这六个数中任意抽取一个,抽取到无理数的概率为 .
17.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为:5、7、9、10、7,则这组数据的众数是 .
18.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
三、解答题(共66分)
19.(本题满分6分)计算:.
20.(本题满分6分)化简:.
21.(本题满分6分)解方程组:.
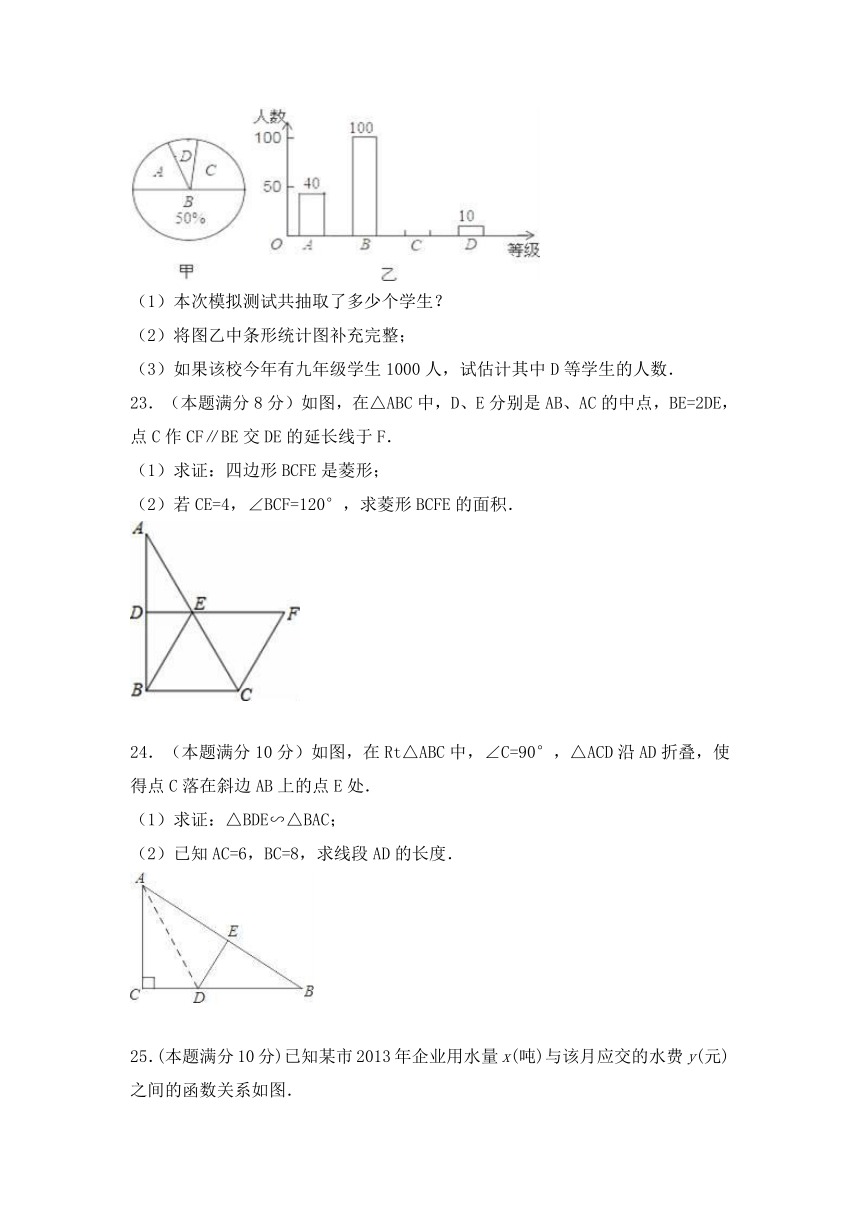
22.(本题满分8分)今年某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
23.(本题满分8分)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE, 点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
24.(本题满分10分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
25.(本题满分10分)已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(第25题图)
(1)当x≥50时,求y关于x的函数表达式.
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量.
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收元.若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
26.(本题满分12分)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(第26题图)
(1)求抛物线的表达式和对称轴.
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
2016年上九年级数学期中考试试题
考生注意:1.本卷共26个题,共120分
2.考试时间为120分钟
一、选择题(本题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.2015的倒数为( )
A. ﹣2015 B. 2015 C. ﹣ D.
2.在数轴上表示﹣3的点与表示3的点之间的距离是( )
. A. 6 B. ﹣6 C. 0 D. ﹣1
3.下列运算正确的是( )
A. a6÷a3=a2 B. 5a2﹣3a2=2a C. (a3)3=a9 D. (a﹣b)2=a2﹣b2
4、已知∠α=37°,那么∠α的余角等于( )
A、37° B、53° C、63° D、143°
5.下列事件是必然事件的是( )
A. 地球绕着太阳转 B. 抛一枚硬币,正面朝上
C. 明天会下雨 D. 打开电视,正在播放新闻
6.一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
A. k>0,b>0 B. k<0,b<0 C. k<0,b>0 D. k>0,b<0
7.设x1,x2是方程x2+5x﹣3=0的两个根,则x12+x22的值是( )
A. 19 B. 25 C. 31 D. 30
8.下列各点中,在函数y=﹣ 图象上的是( )
A. (﹣2,4) B. (2,4) C. (﹣2,﹣4) D. (8,1)
9.下列命题中错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
10.如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=58°,则∠MNH的度数是( )
A A.29° B. 61° C. 34° D. 58°
11.如图,下列条件不能判定△ADB∽△ABC的是( )
A A. ∠ABD=∠ACB B B. ∠ADB=∠ABC C C. AB2=AD AC D. =
12.如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
A A. 80° B. 100° C. 60° D. 40°
二、填空题(本题共6小题,每小题3分,满分18分)
13.计算:33﹣(﹣3)= .
14. 多项式a2﹣4因式分解的结果是 .
15.在平面直角坐标系中,点(-3,2)关于轴的对称点的坐标是 .
16. 从﹣1、0、、0.3、π、 这六个数中任意抽取一个,抽取到无理数的概率为 .
17.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为:5、7、9、10、7,则这组数据的众数是 .
18.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
三、解答题(共66分)
19.(本题满分6分)计算:.
20.(本题满分6分)化简:.
21.(本题满分6分)解方程组:.
22.(本题满分8分)今年某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
23.(本题满分8分)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE, 点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
24.(本题满分10分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
25.(本题满分10分)已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(第25题图)
(1)当x≥50时,求y关于x的函数表达式.
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量.
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收元.若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
26.(本题满分12分)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(第26题图)
(1)求抛物线的表达式和对称轴.
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
答案:
DACBA CCACA DB
13.30 14.(a+2)(a-2) 15.(3,2) 16.
17.7 18.AD=CD或BD平分∠ABC
19.原式=1+
20.原式=x+1
21.
22.解:(1)∵B等人数为100人,所占比例为50%,
∴抽取的学生数=100÷50%=200(名);
(2)C等的人数=200﹣100﹣40﹣10=50(人);
如图所示:
(3)D等学生所占的百分比为: =5%,
故该校今年有九年级学生1000人,其中D等学生的人数为:1000×5%=50(人).
23. (1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,BC=2DE.
∵CF∥BE,
∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,
∴BE=BC.
∴ BCFE是菱形;
(2)连结BF交CE于点O.
∵四边形BCFE是菱形,∠BCF=120°,
∴∠BCE=∠FCE=60°,BF⊥CE,
∴△BCE是等边三角形.
∴BC=CE=4.
∴.
∴.
24. 证明:(1)∵∠C=90°,△ACD沿AD折叠,∴∠C=∠AED=90°,∴∠DEB=∠C=90°,∵∠B=∠B,∴△BDE∽△BAC;(2)由勾股定理得,AB=10.由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.∴BE=AB﹣AE=10﹣6=4,在Rt△BDE中,由勾股定理得,DE2+BE2=BD2,即CD2+42=(8﹣CD)2,解得:CD=3,在Rt△ACD中,由勾股定理得AC2+CD2=AD2,即32+62=AD2,解得:AD=.
25.解:(1)设y关于x的函数表达式y=kx+b.
∵直线y=kx+b经过点(50,200),(60,260),
∴解得
∴y关于x的函数表达式是y=6x-100.
(2)由图可知,当y=620时,x>50,
∴6x-100=620,解得x=120.
答:该企业2013年10月份的用水量为120吨.
(3)由题意,得6x-100+(x-80)=600,
化简,得x2+40x-14000=0,
解得x1=100,x2=-140(不合题意,舍去).
答:这个企业2014年3月份的用水量是100吨.
26.解:(1)根据已知条件可设抛物线的表达式为y=a(x-1)(x-5),
把点A(0,4)的坐标代入,得a=,
∴y=(x-1)(x-5)=x2-x+4=(x-3)2-,
∴抛物线的对称轴是直线x=3.
(2)存在.
∵点A(0,4),抛物线的对称轴是直线x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4).
如解图①,连结BA′交对称轴于点P,连结AP,此时△PAB的周长最小.
(第26题图解①)
设直线BA′的函数表达式为y=kx+b,
把点A′(6,4),B(1,0)的坐标代入,得
解得
∴y=x-.
∵点P的横坐标为3,
∴点P的纵坐标为y=×3-=,
∴点P(3,).
(3)在直线AC下方的抛物线上存在点N,使△NAC面积最大.
设点N的横坐标为t,此时点N(t,t2-t+4)(1<t<5),
如解图②,过点N作NG∥y轴交AC于G,交BC于点F;作AD⊥NG于D,
(第26题图解②)
由点A(0,4)和点C(5,0)可求出直线AC的函数表达式为y=-x+4,
把x=t代入,得y=-t+4,则点G(t,-t+4),
此时:NG=-t+4-(t2-t+4)=-t2+4t.
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CNG=AD·NG+NG·CF=NG·OC=×(-t2+4t)×5=-2t2+10t=-2(t-)2+,
∴当t=时,△CAN的面积最大,最大值为,
当t=时,y=t2-t+4=-3,
∴点N(,-3).
考生注意:1.本卷共26个题,共120分
2.考试时间为120分钟
一、选择题(本题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.2015的倒数为( )
A. ﹣2015 B. 2015 C. ﹣ D.
2.在数轴上表示﹣3的点与表示3的点之间的距离是( )
A. 6 B. ﹣6 C. 0 D.﹣1
3.下列运算正确的是( )
A. a6÷a3=a2 B. 5a2﹣3a2=2a C. (a3)3=a9 D. (a﹣b)2=a2﹣b2
4、已知∠α=37°,那么∠α的余角等于( )
A、37° B、53° C、63° D、143°
5.下列事件是必然事件的是( )
A. 地球绕着太阳转 B. 抛一枚硬币,正面朝上
C. 明天会下雨 D. 打开电视,正在播放新闻
6.一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
A. k>0,b>0 B. k<0,b<0 C. k<0,b>0 D. k>0,b<0
7.设x1,x2是方程x2+5x﹣3=0的两个根,则x12+x22的值是( )
A. 19 B. 25 C. 31 D. 30
8.下列各点中,在函数y=﹣图象上的是( )
A. (﹣2,4) B. (2,4) C. (﹣2,﹣4) D. (8,1)
9.下列命题中错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
10.如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=58°,则∠MNH的度数是( )
A. 29° B. 61° C. 34° D. 58°
11.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D.=
12.如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
A. 80° B.100° C.60° D.40°
二、填空题(本题共6小题,每小题3分,满分18分)
13.计算:33﹣(﹣3)= .
14. 多项式a2﹣4因式分解的结果是 .
15.在平面直角坐标系中,点(-3,2)关于轴的对称点的坐标是 .
16. 从﹣1、0、、0.3、π、这六个数中任意抽取一个,抽取到无理数的概率为 .
17.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为:5、7、9、10、7,则这组数据的众数是 .
18.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
三、解答题(共66分)
19.(本题满分6分)计算:.
20.(本题满分6分)化简:.
21.(本题满分6分)解方程组:.
22.(本题满分8分)今年某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
23.(本题满分8分)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE, 点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
24.(本题满分10分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
25.(本题满分10分)已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(第25题图)
(1)当x≥50时,求y关于x的函数表达式.
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量.
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收元.若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
26.(本题满分12分)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(第26题图)
(1)求抛物线的表达式和对称轴.
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
2016年上九年级数学期中考试试题
考生注意:1.本卷共26个题,共120分
2.考试时间为120分钟
一、选择题(本题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.2015的倒数为( )
A. ﹣2015 B. 2015 C. ﹣ D.
2.在数轴上表示﹣3的点与表示3的点之间的距离是( )
. A. 6 B. ﹣6 C. 0 D. ﹣1
3.下列运算正确的是( )
A. a6÷a3=a2 B. 5a2﹣3a2=2a C. (a3)3=a9 D. (a﹣b)2=a2﹣b2
4、已知∠α=37°,那么∠α的余角等于( )
A、37° B、53° C、63° D、143°
5.下列事件是必然事件的是( )
A. 地球绕着太阳转 B. 抛一枚硬币,正面朝上
C. 明天会下雨 D. 打开电视,正在播放新闻
6.一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
A. k>0,b>0 B. k<0,b<0 C. k<0,b>0 D. k>0,b<0
7.设x1,x2是方程x2+5x﹣3=0的两个根,则x12+x22的值是( )
A. 19 B. 25 C. 31 D. 30
8.下列各点中,在函数y=﹣ 图象上的是( )
A. (﹣2,4) B. (2,4) C. (﹣2,﹣4) D. (8,1)
9.下列命题中错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
10.如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=58°,则∠MNH的度数是( )
A A.29° B. 61° C. 34° D. 58°
11.如图,下列条件不能判定△ADB∽△ABC的是( )
A A. ∠ABD=∠ACB B B. ∠ADB=∠ABC C C. AB2=AD AC D. =
12.如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
A A. 80° B. 100° C. 60° D. 40°
二、填空题(本题共6小题,每小题3分,满分18分)
13.计算:33﹣(﹣3)= .
14. 多项式a2﹣4因式分解的结果是 .
15.在平面直角坐标系中,点(-3,2)关于轴的对称点的坐标是 .
16. 从﹣1、0、、0.3、π、 这六个数中任意抽取一个,抽取到无理数的概率为 .
17.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为:5、7、9、10、7,则这组数据的众数是 .
18.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
三、解答题(共66分)
19.(本题满分6分)计算:.
20.(本题满分6分)化简:.
21.(本题满分6分)解方程组:.
22.(本题满分8分)今年某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
23.(本题满分8分)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE, 点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
24.(本题满分10分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
25.(本题满分10分)已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(第25题图)
(1)当x≥50时,求y关于x的函数表达式.
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量.
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收元.若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
26.(本题满分12分)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(第26题图)
(1)求抛物线的表达式和对称轴.
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
答案:
DACBA CCACA DB
13.30 14.(a+2)(a-2) 15.(3,2) 16.
17.7 18.AD=CD或BD平分∠ABC
19.原式=1+
20.原式=x+1
21.
22.解:(1)∵B等人数为100人,所占比例为50%,
∴抽取的学生数=100÷50%=200(名);
(2)C等的人数=200﹣100﹣40﹣10=50(人);
如图所示:
(3)D等学生所占的百分比为: =5%,
故该校今年有九年级学生1000人,其中D等学生的人数为:1000×5%=50(人).
23. (1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,BC=2DE.
∵CF∥BE,
∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,
∴BE=BC.
∴ BCFE是菱形;
(2)连结BF交CE于点O.
∵四边形BCFE是菱形,∠BCF=120°,
∴∠BCE=∠FCE=60°,BF⊥CE,
∴△BCE是等边三角形.
∴BC=CE=4.
∴.
∴.
24. 证明:(1)∵∠C=90°,△ACD沿AD折叠,∴∠C=∠AED=90°,∴∠DEB=∠C=90°,∵∠B=∠B,∴△BDE∽△BAC;(2)由勾股定理得,AB=10.由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.∴BE=AB﹣AE=10﹣6=4,在Rt△BDE中,由勾股定理得,DE2+BE2=BD2,即CD2+42=(8﹣CD)2,解得:CD=3,在Rt△ACD中,由勾股定理得AC2+CD2=AD2,即32+62=AD2,解得:AD=.
25.解:(1)设y关于x的函数表达式y=kx+b.
∵直线y=kx+b经过点(50,200),(60,260),
∴解得
∴y关于x的函数表达式是y=6x-100.
(2)由图可知,当y=620时,x>50,
∴6x-100=620,解得x=120.
答:该企业2013年10月份的用水量为120吨.
(3)由题意,得6x-100+(x-80)=600,
化简,得x2+40x-14000=0,
解得x1=100,x2=-140(不合题意,舍去).
答:这个企业2014年3月份的用水量是100吨.
26.解:(1)根据已知条件可设抛物线的表达式为y=a(x-1)(x-5),
把点A(0,4)的坐标代入,得a=,
∴y=(x-1)(x-5)=x2-x+4=(x-3)2-,
∴抛物线的对称轴是直线x=3.
(2)存在.
∵点A(0,4),抛物线的对称轴是直线x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4).
如解图①,连结BA′交对称轴于点P,连结AP,此时△PAB的周长最小.
(第26题图解①)
设直线BA′的函数表达式为y=kx+b,
把点A′(6,4),B(1,0)的坐标代入,得
解得
∴y=x-.
∵点P的横坐标为3,
∴点P的纵坐标为y=×3-=,
∴点P(3,).
(3)在直线AC下方的抛物线上存在点N,使△NAC面积最大.
设点N的横坐标为t,此时点N(t,t2-t+4)(1<t<5),
如解图②,过点N作NG∥y轴交AC于G,交BC于点F;作AD⊥NG于D,
(第26题图解②)
由点A(0,4)和点C(5,0)可求出直线AC的函数表达式为y=-x+4,
把x=t代入,得y=-t+4,则点G(t,-t+4),
此时:NG=-t+4-(t2-t+4)=-t2+4t.
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CNG=AD·NG+NG·CF=NG·OC=×(-t2+4t)×5=-2t2+10t=-2(t-)2+,
∴当t=时,△CAN的面积最大,最大值为,
当t=时,y=t2-t+4=-3,
∴点N(,-3).
同课章节目录
