9.4.1 利用角的关系判定两个三角形相似(学案含答案)
文档属性
| 名称 | 9.4.1 利用角的关系判定两个三角形相似(学案含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 780.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.4.1 利用角的关系判定两个三角形相似(学案含答案)
列清单·划重点
知识点1 相似三角形的定义
三角分别 ,三边 的两个三角形叫做相似三角形.△ABC相似于△A'B'C',记作△ABC △A'B'C'.
注意
(1)对应性:通常把表示对应顶点的字母写在对应位置上,这样写容易找到相似三角形的对应角和对应边.
(2)相似三角形的定义既是相似三角形的性质,也是相似三角形的判定.
(3)相似三角形具有传递性:若△ABC∽△A'B'C',△A'B'C'∽△A"B"C",则 △ABC∽△A"B"C".
知识点2 相似三角形的相似比
相似三角形 的比,叫做相似比.
注意
(1)相似比是有顺序的,若△ABC与△A'B'C'的相似比为k,则△A'B'C'与△ABC的相似比为 /k.若这两个相似比相等,即 则相似比为1,此时,这两个三角形全等.也就是说,全等是一种特殊的相似,特殊在相似比为1.(2)全等一定相似,相似不一定全等.
知识点3 三角形相似的条件
相似三角形的判定定理(一):
两角分别 的两个三角形相似.
符号语言:如图所示,
∵∠A=∠A',∠B=∠B',∴△ABC∽△A'B'C'.
注意
两种特殊情况的相似:①有一个锐角相等的两个直角三角形相似;②顶角相等的两个等腰三角形相似.
明考点·识方法
考点1 相似三角形判定定理一
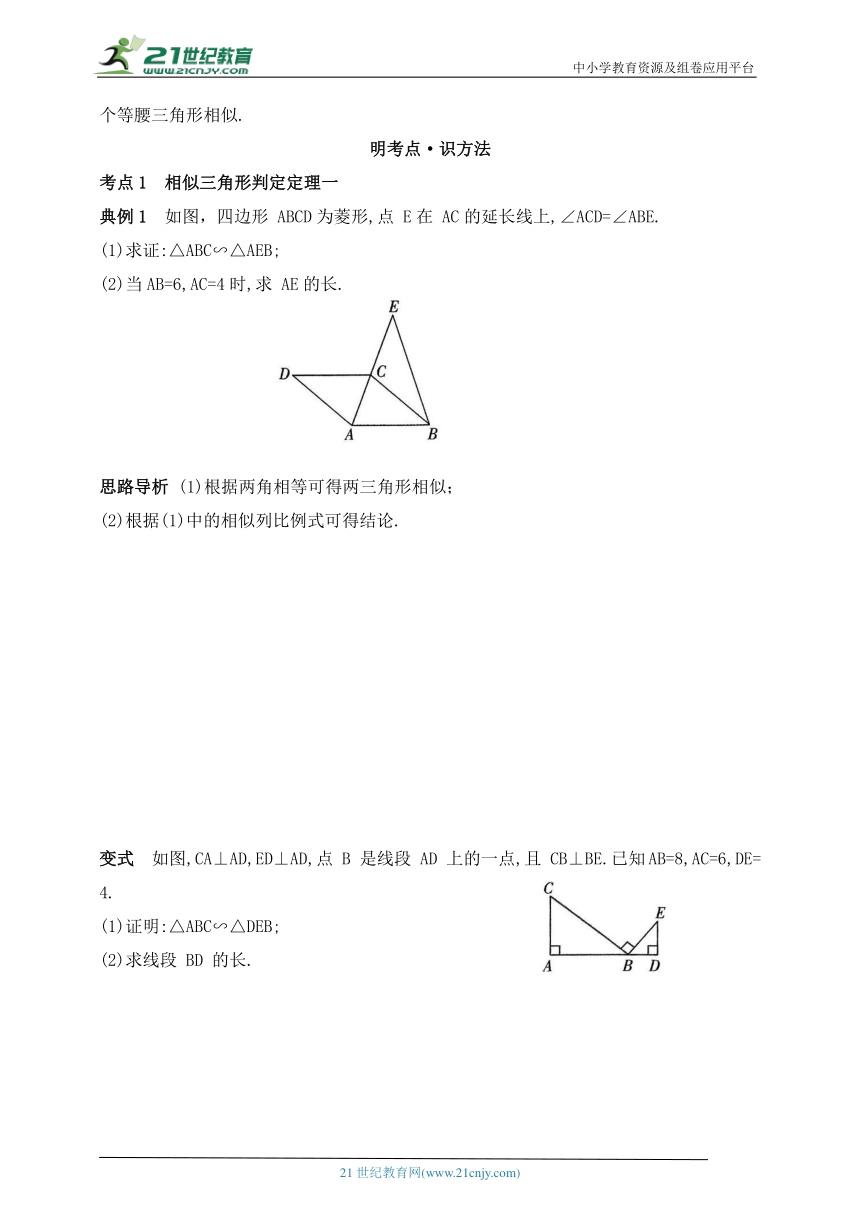
典例1 如图,四边形 ABCD为菱形,点 E在 AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
(2)当AB=6,AC=4时,求 AE的长.
思路导析 (1)根据两角相等可得两三角形相似;
(2)根据(1)中的相似列比例式可得结论.
变式 如图,CA⊥AD,ED⊥AD,点 B 是线段 AD 上的一点,且 CB⊥BE.已知AB=8,AC=6,DE=4.
(1)证明:△ABC∽△DEB;
(2)求线段 BD 的长.
考点2 相似三角形判定定理一的应用
典例2 如图,∠ABD=∠BCD=90°,DB 平分∠ADC,过点 B 作 BM ∥CD 交AD 于点 M.连接CM交 DB 于点 N.
(1)求证:
(2)若CD=6,AD=8,求 MN的长.
思路导析 (1)通过证明△ABD∽△BCD,可得可得结论;
(2)由平行线的性质可证∠MBD=∠BDC,即可证AM=MD=MB=4,由. 和勾股定理 可求 MC 的长,通过 证明 △MNB∽△CND,可得 即可求MN的长.
变式 如图,在△ABC中,AD平分∠BAC交BC 于点 D,F为AD 上一点,且 BF=BD.BF的延长线交AC于点E.
(1)求证:AB·AD=AF·AC;
(2)若∠BAC=60°,AB=4,AC=6,求 DF的长.
当堂测·夯基础
1.如图,在△ABC中,点 D在AB 边上,点 E 在AC边上,且∠1=∠2=∠3,则下列结论中不正确的是 ( )
A.△ADE∽△ABC B.△ADE∽△ACD C.△ADE∽△EDC D.△ABC∽△ACD
第1题图 第2题图
2.如图, 在 ABCD中,对角线 AC,BD 相交于点O,点 E 为OC 的中点,EF∥AB 交BC 于点F.若AB=4,则 EF的长为 ( )
A. B.1 C. D.2
3.如图,在△ABC 中,点 D,E分别在边AB,AC上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
第3题图 第4题图
4.在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片 ABCD 如图所示,点N 在边 AD 上,现将矩形折叠,折痕为 BN,点A 对应的点记为点 M,若点M恰好落在边 DC上,则图中与△NDM一定相似的三角形是 .
5.如图,在菱形ABCD中,E 为CD 延长线上一点,连接BE交AD 于点 F,∠AEB=∠C.
(1)求证:△ABE∽△BEC;
(2)若AE=4,BE=8,求CE的长.
参考答案
【列清单·划重点】
知识点1 相等 对应成比例 ∽
知识点2 对应边
知识点3 相等
【明考点·识方法】
典例1 解:(1)证明:∵四边形 ABCD 为菱形,∴∠ACD=∠BCA,
∵∠ACD=∠ABE,∴∠BCA=∠ABE,
∵∠BAC=∠EAB,∴△ABC∽△AEB;
(2)∵△ABC∽△AEB,∴ABE=AC,
变式 解:(1)证明:∵ CA⊥AD,ED⊥ AD,CB⊥BE,∴∠A=∠CBE=∠D=90°,
∴∠C+∠CBA=90°,∠CBA+∠DBE=90°,∴∠C=∠DBE,∴△ABC∽△DEB;
(2)∵△ABC∽△DEB,∴ACD=ABE,
典例2 证明:(1)∵DB平分∠ADC,∴∠ADB=∠CDB,且∠ABD=∠BCD=90°,
∴△ABD∽△BCD,∴AD=BD,
(2)∵BM∥CD,∴∠MBD=∠BDC,∴∠ADB=∠MBD,且∠ABD=90°,
∴BM=MD,∠MAB=∠MBA,∴BM=MD=AM=4,
∵BD =AD·CD,且CD=6,AD=8,
,
∵BM∥CD,∴∠BMN=∠DCN,
又∵∠MNB=∠CND,∴△MNB∽△CND,
变式 解:(1)证明:∵AD平分∠BAC,∴∠BAF=∠DAC,
又∵BF=BD,∴∠BFD=∠FDB,∴∠AFB=∠ADC,∴△AFB∽△ADC,
∴AB·AD=AF·AC;
(2)作 BH⊥AD于点 H,作 CN⊥AD于点 N,
则
∵∠BDH=∠CDN,∴△BHD∽△CND.
又∵BF=BD,BH⊥DF,
【当堂测·夯基础】
1. C 2. B 3.∠ADE=∠C(答案不唯一) 4.△MCB
5.解:(1)证明:在菱形ABCD中,∵AB∥CD,∴∠ABE=∠CEB,
又∵∠AEB=∠C,∴△ABE∽△BEC;
(2)∵△ABE∽△BEC,
∵AE=4,BE=8,AB=BC,
即CE的长为8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.4.1 利用角的关系判定两个三角形相似(学案含答案)
列清单·划重点
知识点1 相似三角形的定义
三角分别 ,三边 的两个三角形叫做相似三角形.△ABC相似于△A'B'C',记作△ABC △A'B'C'.
注意
(1)对应性:通常把表示对应顶点的字母写在对应位置上,这样写容易找到相似三角形的对应角和对应边.
(2)相似三角形的定义既是相似三角形的性质,也是相似三角形的判定.
(3)相似三角形具有传递性:若△ABC∽△A'B'C',△A'B'C'∽△A"B"C",则 △ABC∽△A"B"C".
知识点2 相似三角形的相似比
相似三角形 的比,叫做相似比.
注意
(1)相似比是有顺序的,若△ABC与△A'B'C'的相似比为k,则△A'B'C'与△ABC的相似比为 /k.若这两个相似比相等,即 则相似比为1,此时,这两个三角形全等.也就是说,全等是一种特殊的相似,特殊在相似比为1.(2)全等一定相似,相似不一定全等.
知识点3 三角形相似的条件
相似三角形的判定定理(一):
两角分别 的两个三角形相似.
符号语言:如图所示,
∵∠A=∠A',∠B=∠B',∴△ABC∽△A'B'C'.
注意
两种特殊情况的相似:①有一个锐角相等的两个直角三角形相似;②顶角相等的两个等腰三角形相似.
明考点·识方法
考点1 相似三角形判定定理一
典例1 如图,四边形 ABCD为菱形,点 E在 AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
(2)当AB=6,AC=4时,求 AE的长.
思路导析 (1)根据两角相等可得两三角形相似;
(2)根据(1)中的相似列比例式可得结论.
变式 如图,CA⊥AD,ED⊥AD,点 B 是线段 AD 上的一点,且 CB⊥BE.已知AB=8,AC=6,DE=4.
(1)证明:△ABC∽△DEB;
(2)求线段 BD 的长.
考点2 相似三角形判定定理一的应用
典例2 如图,∠ABD=∠BCD=90°,DB 平分∠ADC,过点 B 作 BM ∥CD 交AD 于点 M.连接CM交 DB 于点 N.
(1)求证:
(2)若CD=6,AD=8,求 MN的长.
思路导析 (1)通过证明△ABD∽△BCD,可得可得结论;
(2)由平行线的性质可证∠MBD=∠BDC,即可证AM=MD=MB=4,由. 和勾股定理 可求 MC 的长,通过 证明 △MNB∽△CND,可得 即可求MN的长.
变式 如图,在△ABC中,AD平分∠BAC交BC 于点 D,F为AD 上一点,且 BF=BD.BF的延长线交AC于点E.
(1)求证:AB·AD=AF·AC;
(2)若∠BAC=60°,AB=4,AC=6,求 DF的长.
当堂测·夯基础
1.如图,在△ABC中,点 D在AB 边上,点 E 在AC边上,且∠1=∠2=∠3,则下列结论中不正确的是 ( )
A.△ADE∽△ABC B.△ADE∽△ACD C.△ADE∽△EDC D.△ABC∽△ACD
第1题图 第2题图
2.如图, 在 ABCD中,对角线 AC,BD 相交于点O,点 E 为OC 的中点,EF∥AB 交BC 于点F.若AB=4,则 EF的长为 ( )
A. B.1 C. D.2
3.如图,在△ABC 中,点 D,E分别在边AB,AC上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
第3题图 第4题图
4.在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片 ABCD 如图所示,点N 在边 AD 上,现将矩形折叠,折痕为 BN,点A 对应的点记为点 M,若点M恰好落在边 DC上,则图中与△NDM一定相似的三角形是 .
5.如图,在菱形ABCD中,E 为CD 延长线上一点,连接BE交AD 于点 F,∠AEB=∠C.
(1)求证:△ABE∽△BEC;
(2)若AE=4,BE=8,求CE的长.
参考答案
【列清单·划重点】
知识点1 相等 对应成比例 ∽
知识点2 对应边
知识点3 相等
【明考点·识方法】
典例1 解:(1)证明:∵四边形 ABCD 为菱形,∴∠ACD=∠BCA,
∵∠ACD=∠ABE,∴∠BCA=∠ABE,
∵∠BAC=∠EAB,∴△ABC∽△AEB;
(2)∵△ABC∽△AEB,∴ABE=AC,
变式 解:(1)证明:∵ CA⊥AD,ED⊥ AD,CB⊥BE,∴∠A=∠CBE=∠D=90°,
∴∠C+∠CBA=90°,∠CBA+∠DBE=90°,∴∠C=∠DBE,∴△ABC∽△DEB;
(2)∵△ABC∽△DEB,∴ACD=ABE,
典例2 证明:(1)∵DB平分∠ADC,∴∠ADB=∠CDB,且∠ABD=∠BCD=90°,
∴△ABD∽△BCD,∴AD=BD,
(2)∵BM∥CD,∴∠MBD=∠BDC,∴∠ADB=∠MBD,且∠ABD=90°,
∴BM=MD,∠MAB=∠MBA,∴BM=MD=AM=4,
∵BD =AD·CD,且CD=6,AD=8,
,
∵BM∥CD,∴∠BMN=∠DCN,
又∵∠MNB=∠CND,∴△MNB∽△CND,
变式 解:(1)证明:∵AD平分∠BAC,∴∠BAF=∠DAC,
又∵BF=BD,∴∠BFD=∠FDB,∴∠AFB=∠ADC,∴△AFB∽△ADC,
∴AB·AD=AF·AC;
(2)作 BH⊥AD于点 H,作 CN⊥AD于点 N,
则
∵∠BDH=∠CDN,∴△BHD∽△CND.
又∵BF=BD,BH⊥DF,
【当堂测·夯基础】
1. C 2. B 3.∠ADE=∠C(答案不唯一) 4.△MCB
5.解:(1)证明:在菱形ABCD中,∵AB∥CD,∴∠ABE=∠CEB,
又∵∠AEB=∠C,∴△ABE∽△BEC;
(2)∵△ABE∽△BEC,
∵AE=4,BE=8,AB=BC,
即CE的长为8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
