9.4.3 利用边的关系判定两个三角形相似(学案含答案)
文档属性
| 名称 | 9.4.3 利用边的关系判定两个三角形相似(学案含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 405.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 09:43:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.4.3 利用边的关系判定两个三角形相似(学案含答案)
列清单·划重点
知识点 相似三角形的判定定理三
1.定理:
三边 的两个三角形相似.
2.符号语言
如图所示,
如果 那么△ABC △A'B'C'.
注意
(1)当已知条件中有三边时,可考虑此判定方法.在判断三边是否成比例时,应先将三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定这两个三角形是否相似.
(2)特别地,若两个直角三角形的斜边和一条直角边对应成比例,则这两个直角三角形相似.
明考点·识方法
考点1 利用相似三角形判定定理三判定三角形相似
典例1 如图所示,网格中相似的两个三角形是 ( )
A.①与② B.①与③ C.③与④ D.②与③
思路导析 用勾股定理求出两个三角形的各边长,通过三边成比例,判定两个三角形相似.
变式 如图,方格纸中每个小正方形的边长为1,△ABC和△DEF 的顶点都在格点上(小正方形的顶点).是△DEF边上的5个格点,请在这5个格点中选取2个作为三角形的顶点,使它们和点 D 构成的三角形与△ABC 相似,所有符合条件的三角形的个数为 ( )
A.2个 B.3个 C.4个 D.5个
考点2 相似三角形判定定理三的应用
典例2 一个三角形木架三边长分别是75 cm,100 cm,120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
思路导析 根据相似三角形对应边成比例,进行分类讨论求解.
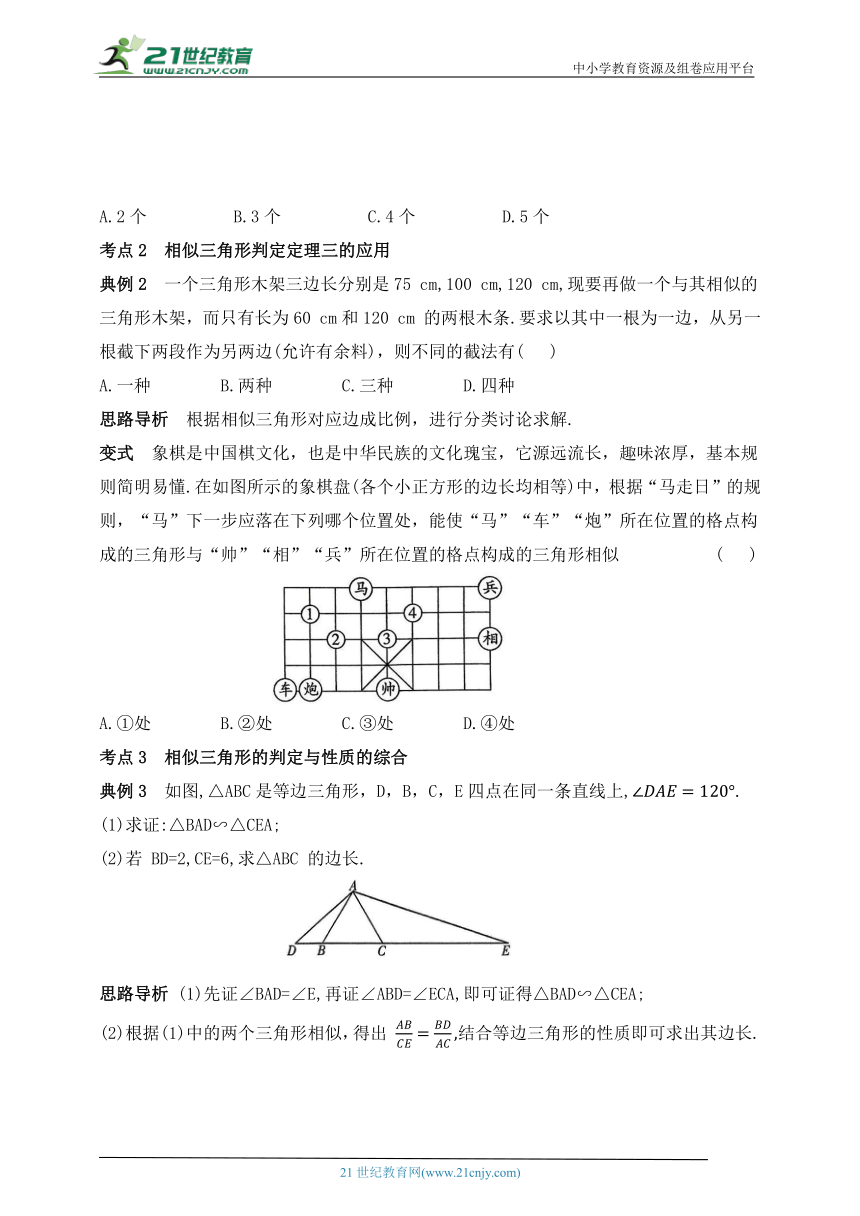
变式 象棋是中国棋文化,也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”下一步应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似 ( )
A.①处 B.②处 C.③处 D.④处
考点3 相似三角形的判定与性质的综合
典例3 如图,△ABC是等边三角形,D,B,C,E四点在同一条直线上,.
(1)求证:△BAD∽△CEA;
(2)若 BD=2,CE=6,求△ABC 的边长.
思路导析 (1)先证∠BAD=∠E,再证∠ABD=∠ECA,即可证得△BAD∽△CEA;
(2)根据(1)中的两个三角形相似,得出 结合等边三角形的性质即可求出其边长.
变式 如图,在Rt△ABC中,∠ACB =90°,CD 是△ABC的中线,作 AE⊥CD 于点 E,EF∥BC 交BD 于点F.
(1)求证:△ACE∽△BAC;
(2)若AC= ,CE=1,求 BD及EF 的长.
当堂测·夯基础
1.已知△ABC 的三边长分别为1,,,△DEF 的三边长分别则△ABC与△DEF ( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判定是否相似
2.如图在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形,现从△ABC的三个顶点中选取两个格点,再从余下的格点中选取一个格点连接成格点三角形,其中与△ABC 相似的有 ( )
A.1个 B.2个 C.3个 D.4个
3.已知△ABC的三边长分别为6 cm,7. 5cm ,9 cm,△DEF 的一边长为4 cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似 ( )
A.2 cm,3 cm B.4 cm,5 cm C.5 cm,6 cm D.6 cm,7 cm
4.如图,在平行四边形ABCD 中,连接对角线 AC,延长 AB 至点E,使 BE=AB,连接 DE,分别交 BC,AC于点F,G.若 BC=6,DG=4,求 FG的长为 .
参考答案
【列清单·划重点】
知识点 1.对应成比例 2.∽
【明考点·识方法】
典例1 B
解析:图形①的三边为2, 图形②的三边为 图形③的三边为2,2,2图形④的三边为3,,
∴①与③相似.
变式 B
典例2 B 变式 B
典例3 解:(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ABC=∠ACB=60°,
∵∠DAE=120°,∴∠BAD+∠CAE=60°,
∵∠ACB是△ACE的外角,∴∠ACB=∠E+∠CAE=60°,∴∠BAD=∠E,
∵∠ABC=∠ACB=60°,∴∠ABD=∠ECA=120°,∴△BAD∽△CEA;
(2)由(1)知△BAD∽△CEA,∴△E=BC,
∵△ABC是等边三角形,∴AB=AC,
,即△ABC的边长为
变式 解:(1)证明:∵CD 是△ABC的中线,∴AD=CD,∴∠CAD=∠ACD,
∵ AE⊥CD,∴∠AEC=∠ACB=90°,∴△ACE∽△BAC;
(2)∵△ACE∽△BAC,即 解得AB=5,
∵CD是△ABC的中线,
∵EF∥BC,∴∠DEF=∠DCB,
又∵∠EDF=∠CDB,∴△DEF∽△DCB,即 解得
【当堂测·夯基础】
1. A 2. C 3. C 4. 2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.4.3 利用边的关系判定两个三角形相似(学案含答案)
列清单·划重点
知识点 相似三角形的判定定理三
1.定理:
三边 的两个三角形相似.
2.符号语言
如图所示,
如果 那么△ABC △A'B'C'.
注意
(1)当已知条件中有三边时,可考虑此判定方法.在判断三边是否成比例时,应先将三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定这两个三角形是否相似.
(2)特别地,若两个直角三角形的斜边和一条直角边对应成比例,则这两个直角三角形相似.
明考点·识方法
考点1 利用相似三角形判定定理三判定三角形相似
典例1 如图所示,网格中相似的两个三角形是 ( )
A.①与② B.①与③ C.③与④ D.②与③
思路导析 用勾股定理求出两个三角形的各边长,通过三边成比例,判定两个三角形相似.
变式 如图,方格纸中每个小正方形的边长为1,△ABC和△DEF 的顶点都在格点上(小正方形的顶点).是△DEF边上的5个格点,请在这5个格点中选取2个作为三角形的顶点,使它们和点 D 构成的三角形与△ABC 相似,所有符合条件的三角形的个数为 ( )
A.2个 B.3个 C.4个 D.5个
考点2 相似三角形判定定理三的应用
典例2 一个三角形木架三边长分别是75 cm,100 cm,120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
思路导析 根据相似三角形对应边成比例,进行分类讨论求解.
变式 象棋是中国棋文化,也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”下一步应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似 ( )
A.①处 B.②处 C.③处 D.④处
考点3 相似三角形的判定与性质的综合
典例3 如图,△ABC是等边三角形,D,B,C,E四点在同一条直线上,.
(1)求证:△BAD∽△CEA;
(2)若 BD=2,CE=6,求△ABC 的边长.
思路导析 (1)先证∠BAD=∠E,再证∠ABD=∠ECA,即可证得△BAD∽△CEA;
(2)根据(1)中的两个三角形相似,得出 结合等边三角形的性质即可求出其边长.
变式 如图,在Rt△ABC中,∠ACB =90°,CD 是△ABC的中线,作 AE⊥CD 于点 E,EF∥BC 交BD 于点F.
(1)求证:△ACE∽△BAC;
(2)若AC= ,CE=1,求 BD及EF 的长.
当堂测·夯基础
1.已知△ABC 的三边长分别为1,,,△DEF 的三边长分别则△ABC与△DEF ( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判定是否相似
2.如图在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形,现从△ABC的三个顶点中选取两个格点,再从余下的格点中选取一个格点连接成格点三角形,其中与△ABC 相似的有 ( )
A.1个 B.2个 C.3个 D.4个
3.已知△ABC的三边长分别为6 cm,7. 5cm ,9 cm,△DEF 的一边长为4 cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似 ( )
A.2 cm,3 cm B.4 cm,5 cm C.5 cm,6 cm D.6 cm,7 cm
4.如图,在平行四边形ABCD 中,连接对角线 AC,延长 AB 至点E,使 BE=AB,连接 DE,分别交 BC,AC于点F,G.若 BC=6,DG=4,求 FG的长为 .
参考答案
【列清单·划重点】
知识点 1.对应成比例 2.∽
【明考点·识方法】
典例1 B
解析:图形①的三边为2, 图形②的三边为 图形③的三边为2,2,2图形④的三边为3,,
∴①与③相似.
变式 B
典例2 B 变式 B
典例3 解:(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ABC=∠ACB=60°,
∵∠DAE=120°,∴∠BAD+∠CAE=60°,
∵∠ACB是△ACE的外角,∴∠ACB=∠E+∠CAE=60°,∴∠BAD=∠E,
∵∠ABC=∠ACB=60°,∴∠ABD=∠ECA=120°,∴△BAD∽△CEA;
(2)由(1)知△BAD∽△CEA,∴△E=BC,
∵△ABC是等边三角形,∴AB=AC,
,即△ABC的边长为
变式 解:(1)证明:∵CD 是△ABC的中线,∴AD=CD,∴∠CAD=∠ACD,
∵ AE⊥CD,∴∠AEC=∠ACB=90°,∴△ACE∽△BAC;
(2)∵△ACE∽△BAC,即 解得AB=5,
∵CD是△ABC的中线,
∵EF∥BC,∴∠DEF=∠DCB,
又∵∠EDF=∠CDB,∴△DEF∽△DCB,即 解得
【当堂测·夯基础】
1. A 2. C 3. C 4. 2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
