9.5 相似三角形判定定理的证明(学案含答案)
文档属性
| 名称 | 9.5 相似三角形判定定理的证明(学案含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 364.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 09:40:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
9.5 相似三角形判定定理的证明(学案含答案)
列清单·划重点
知识点1 三角形相似的判定定理
定理一:两角分别 的两个三角形相似.
定理二:两边 且夹角 的两个三角形相似.
定理三:三边 的两个三角形相似.
知识点2 相似三角形判定定理的证明思路
在较大三角形上构造一个与小三角形全等的“新小三角形”,然后证明“新小三角形”与较大三角形相似.
知识点3 证明三角形相似的一般思路
判断两个三角形相似,要注意从符合判断方法的条件入手,寻求最佳途径,常见思路如下:
(1)若有一组对应角相等,可再找另一组对应角相等,或再找这组角的两邻边对应成比例.
(2)若有两组对应边成比例,可寻找夹角相等,或再找第三组对应边成比例.
(3)条件中若有平行线,可用“两角对应相等的两个三角形相似”进行判断.
(4)若是等腰三角形,可找顶角(或底角)相等,也可找底和腰对应成比例判断相似.
(5)利用三角形相似的传递性:
若,则.
明考点·识方法
考点1 相似三角形判定的简单应用
典例1 如图,点B为线段AC上一点,满足∠A=∠EBD =∠C=90°,AE=1,AB=BC=2.
(1)求CD的长度;
(2)求证:△ABE∽△BDE.
思路导析 (1)由∠ABE+∠AEB=90°=∠ABE+∠CBD,可得∠AEB=∠CBD,证明△ABE∽△CDB,则 即 计算求解即可;
(2)由勾股定理,得 由 ∠EBD=90°,可证结论.
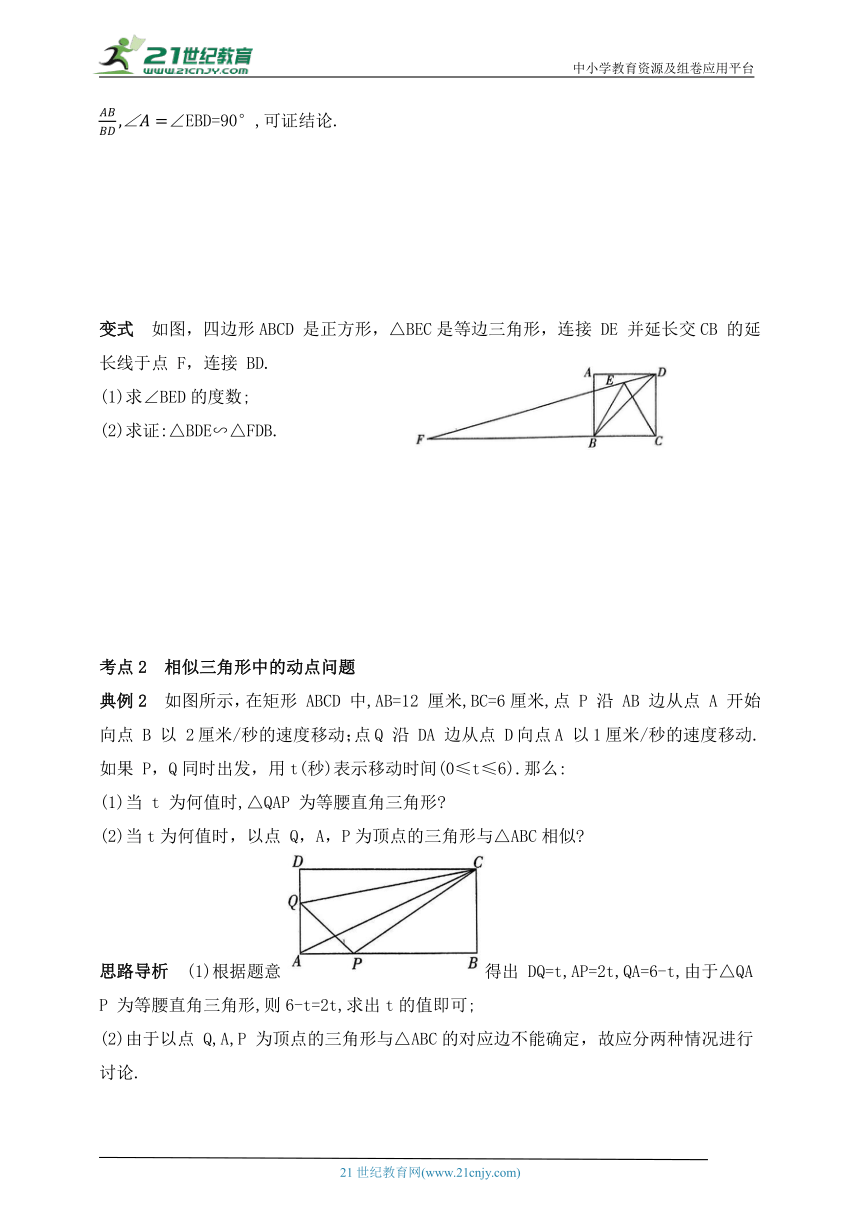
变式 如图,四边形ABCD 是正方形,△BEC是等边三角形,连接 DE 并延长交CB 的延长线于点 F,连接 BD.
(1)求∠BED的度数;
(2)求证:△BDE∽△FDB.
考点2 相似三角形中的动点问题
典例2 如图所示,在矩形 ABCD 中,AB=12 厘米,BC=6厘米,点 P 沿 AB 边从点 A 开始向点 B 以 2厘米/秒的速度移动;点Q 沿 DA 边从点 D向点A 以1厘米/秒的速度移动.如果 P,Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当 t 为何值时,△QAP 为等腰直角三角形
(2)当t为何值时,以点 Q,A,P为顶点的三角形与△ABC相似
思路导析 (1)根据题意得出 DQ=t,AP=2t,QA=6-t,由于△QAP 为等腰直角三角形,则6-t=2t,求出t的值即可;
(2)由于以点 Q,A,P 为顶点的三角形与△ABC的对应边不能确定,故应分两种情况进行讨论.
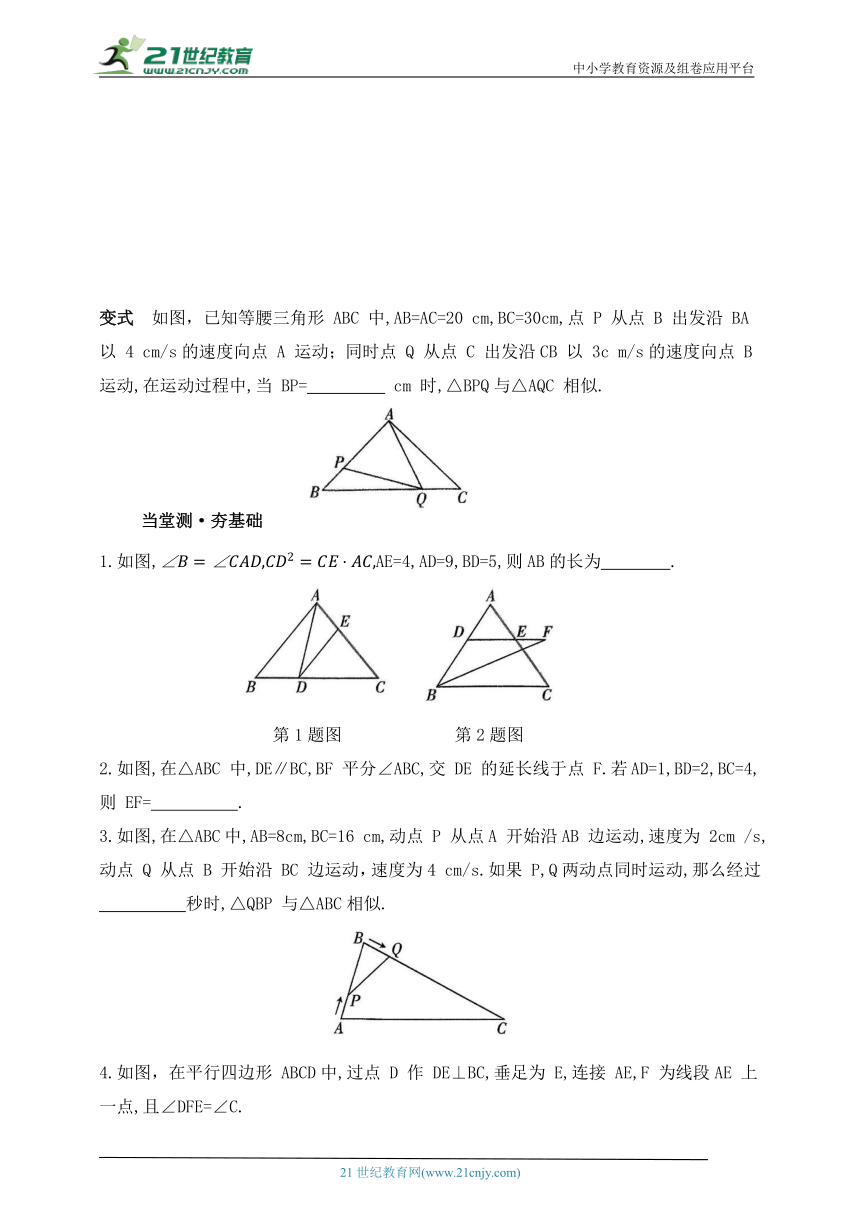
变式 如图,已知等腰三角形 ABC 中,AB=AC=20 cm,BC=30cm,点 P 从点 B 出发沿 BA 以 4 cm/s的速度向点 A 运动;同时点 Q 从点 C 出发沿CB 以 3c m/s的速度向点 B 运动,在运动过程中,当 BP= cm 时,△BPQ与△AQC 相似.
当堂测·夯基础
1.如图,AE=4,AD=9,BD=5,则AB的长为 .
第1题图 第2题图
2.如图,在△ABC 中,DE∥BC,BF 平分∠ABC,交 DE 的延长线于点 F.若AD=1,BD=2,BC=4,则 EF= .
3.如图,在△ABC中,AB=8cm,BC=16 cm,动点 P 从点A 开始沿AB 边运动,速度为 2cm /s,动点 Q 从点 B 开始沿 BC 边运动,速度为4 cm/s.如果 P,Q两动点同时运动,那么经过 秒时,△QBP 与△ABC相似.
4.如图,在平行四边形 ABCD中,过点 D 作 DE⊥BC,垂足为 E,连接 AE,F 为线段AE 上一点,且∠DFE=∠C.
(1)求证:
(2)若 ,求DF的长.
参考答案
【列清单·划重点】
知识点1 相等 成比例 相等 成比例
【明考点·识方法】
典例1 解:(1)∵∠A=∠EBD=∠C=90°,
∴ ∠ABE + ∠AEB = 90°= ∠ABE +∠CBD,即∠AEB=∠CBD,
∴△ABE∽△CDB,即 解得CD=4,∴CD的长度为4;
(2)证明:由勾股定理,得
∴△ABE∽△BDE.
变式 解:(1)∵四边形ABCD 是正方形,∴∠BCD=∠90°,BC=CD,
∵△BCE是等边三角形,∴∠BCE=∠BEC=60°,BC=CE,
,
∴∠BED = ∠BEC + ∠CED = 75°+
(2)证明:∵四边形 ABCD 是正方形,∴∠ABC=90°,∠ABD=45°,
∴∠ABF=90°,
∵∠BED=135°,∴∠BED=∠DBF,
∵∠BDE=∠BDF,∴△BDE∽△FDB.
典例2 解:(1)∵AB=12厘米,BC=6厘米,点 P沿AB 边从点A 开始向点B 以2厘米/秒的速度移动;点Q沿DA 边从点D 向点A 以1厘米/秒的速度移动,
∴DQ=t,AP=2t,QA=6-t,
当△QAP 为等腰直角三角形时6-t=2t,解得t=2;
(2)两种情况:因为∠PAQ=∠B=90°,①当 时,△QAP∽△ABC,即 解得t=1.2(秒);
②当 时,△PAQ∽△ABC时,即 解得t=3(秒).
故当经过 1.2 秒或 3 秒时,△QAP 与△ABC相似.
变式 或20
【当堂测·夯基础】
1. 2. 3. 2或0.8
4.解:(1)证明:∵在 ABCD中,∴AD∥BC,∴∠DAE=∠AEB,
∵在 ABCD中,∴AB∥CD,AD=BC,AB=CD,∴∠B+∠C=180°,
∵∠DFE=∠C,∠AFD+∠DFE=180°,∴∠B=∠AFD,
∴△ADF∽△EAB,
∵AD=BC,AB=CD,∴BC=DCD;
(2)在 Rt△AED中,由勾股定理得AE=
解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.5 相似三角形判定定理的证明(学案含答案)
列清单·划重点
知识点1 三角形相似的判定定理
定理一:两角分别 的两个三角形相似.
定理二:两边 且夹角 的两个三角形相似.
定理三:三边 的两个三角形相似.
知识点2 相似三角形判定定理的证明思路
在较大三角形上构造一个与小三角形全等的“新小三角形”,然后证明“新小三角形”与较大三角形相似.
知识点3 证明三角形相似的一般思路
判断两个三角形相似,要注意从符合判断方法的条件入手,寻求最佳途径,常见思路如下:
(1)若有一组对应角相等,可再找另一组对应角相等,或再找这组角的两邻边对应成比例.
(2)若有两组对应边成比例,可寻找夹角相等,或再找第三组对应边成比例.
(3)条件中若有平行线,可用“两角对应相等的两个三角形相似”进行判断.
(4)若是等腰三角形,可找顶角(或底角)相等,也可找底和腰对应成比例判断相似.
(5)利用三角形相似的传递性:
若,则.
明考点·识方法
考点1 相似三角形判定的简单应用
典例1 如图,点B为线段AC上一点,满足∠A=∠EBD =∠C=90°,AE=1,AB=BC=2.
(1)求CD的长度;
(2)求证:△ABE∽△BDE.
思路导析 (1)由∠ABE+∠AEB=90°=∠ABE+∠CBD,可得∠AEB=∠CBD,证明△ABE∽△CDB,则 即 计算求解即可;
(2)由勾股定理,得 由 ∠EBD=90°,可证结论.
变式 如图,四边形ABCD 是正方形,△BEC是等边三角形,连接 DE 并延长交CB 的延长线于点 F,连接 BD.
(1)求∠BED的度数;
(2)求证:△BDE∽△FDB.
考点2 相似三角形中的动点问题
典例2 如图所示,在矩形 ABCD 中,AB=12 厘米,BC=6厘米,点 P 沿 AB 边从点 A 开始向点 B 以 2厘米/秒的速度移动;点Q 沿 DA 边从点 D向点A 以1厘米/秒的速度移动.如果 P,Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当 t 为何值时,△QAP 为等腰直角三角形
(2)当t为何值时,以点 Q,A,P为顶点的三角形与△ABC相似
思路导析 (1)根据题意得出 DQ=t,AP=2t,QA=6-t,由于△QAP 为等腰直角三角形,则6-t=2t,求出t的值即可;
(2)由于以点 Q,A,P 为顶点的三角形与△ABC的对应边不能确定,故应分两种情况进行讨论.
变式 如图,已知等腰三角形 ABC 中,AB=AC=20 cm,BC=30cm,点 P 从点 B 出发沿 BA 以 4 cm/s的速度向点 A 运动;同时点 Q 从点 C 出发沿CB 以 3c m/s的速度向点 B 运动,在运动过程中,当 BP= cm 时,△BPQ与△AQC 相似.
当堂测·夯基础
1.如图,AE=4,AD=9,BD=5,则AB的长为 .
第1题图 第2题图
2.如图,在△ABC 中,DE∥BC,BF 平分∠ABC,交 DE 的延长线于点 F.若AD=1,BD=2,BC=4,则 EF= .
3.如图,在△ABC中,AB=8cm,BC=16 cm,动点 P 从点A 开始沿AB 边运动,速度为 2cm /s,动点 Q 从点 B 开始沿 BC 边运动,速度为4 cm/s.如果 P,Q两动点同时运动,那么经过 秒时,△QBP 与△ABC相似.
4.如图,在平行四边形 ABCD中,过点 D 作 DE⊥BC,垂足为 E,连接 AE,F 为线段AE 上一点,且∠DFE=∠C.
(1)求证:
(2)若 ,求DF的长.
参考答案
【列清单·划重点】
知识点1 相等 成比例 相等 成比例
【明考点·识方法】
典例1 解:(1)∵∠A=∠EBD=∠C=90°,
∴ ∠ABE + ∠AEB = 90°= ∠ABE +∠CBD,即∠AEB=∠CBD,
∴△ABE∽△CDB,即 解得CD=4,∴CD的长度为4;
(2)证明:由勾股定理,得
∴△ABE∽△BDE.
变式 解:(1)∵四边形ABCD 是正方形,∴∠BCD=∠90°,BC=CD,
∵△BCE是等边三角形,∴∠BCE=∠BEC=60°,BC=CE,
,
∴∠BED = ∠BEC + ∠CED = 75°+
(2)证明:∵四边形 ABCD 是正方形,∴∠ABC=90°,∠ABD=45°,
∴∠ABF=90°,
∵∠BED=135°,∴∠BED=∠DBF,
∵∠BDE=∠BDF,∴△BDE∽△FDB.
典例2 解:(1)∵AB=12厘米,BC=6厘米,点 P沿AB 边从点A 开始向点B 以2厘米/秒的速度移动;点Q沿DA 边从点D 向点A 以1厘米/秒的速度移动,
∴DQ=t,AP=2t,QA=6-t,
当△QAP 为等腰直角三角形时6-t=2t,解得t=2;
(2)两种情况:因为∠PAQ=∠B=90°,①当 时,△QAP∽△ABC,即 解得t=1.2(秒);
②当 时,△PAQ∽△ABC时,即 解得t=3(秒).
故当经过 1.2 秒或 3 秒时,△QAP 与△ABC相似.
变式 或20
【当堂测·夯基础】
1. 2. 3. 2或0.8
4.解:(1)证明:∵在 ABCD中,∴AD∥BC,∴∠DAE=∠AEB,
∵在 ABCD中,∴AB∥CD,AD=BC,AB=CD,∴∠B+∠C=180°,
∵∠DFE=∠C,∠AFD+∠DFE=180°,∴∠B=∠AFD,
∴△ADF∽△EAB,
∵AD=BC,AB=CD,∴BC=DCD;
(2)在 Rt△AED中,由勾股定理得AE=
解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
