9.9.1 位似图形(学案含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
9.9.1 位似图形(学案含答案)
列清单·划重点
知识点1 位似多边形的概念
如果两个相似多边形任意一组 A,A'的连线都经过 ,且有( ·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O 叫做位似中心,k就是这两个相似多边形的
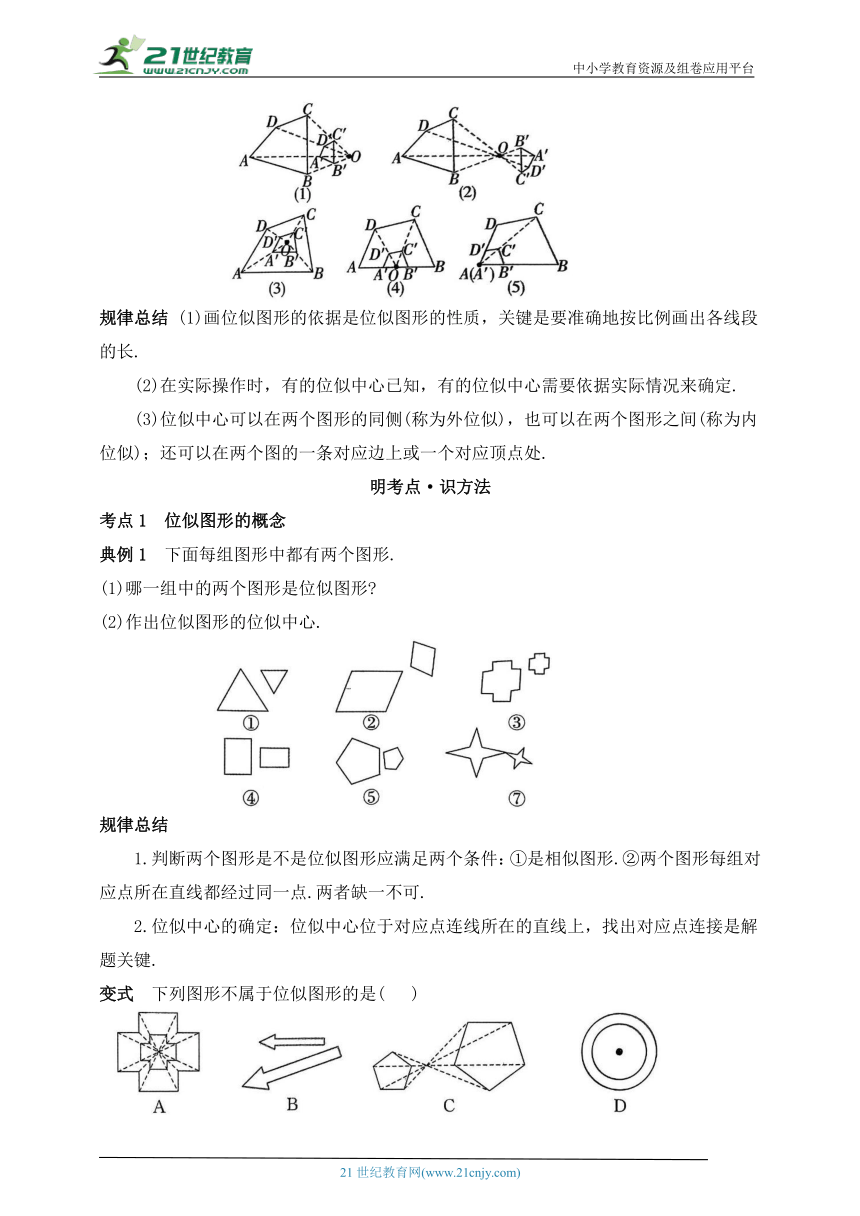
如图1,图2所示的图形都是位似图形,
注意
(1)位似图形是相似图形,是增加了条件的相似图形,这个条件就是:每组对应点所在直线都经过同一个点.而相似图形不一定是位似图形;
(2)两个位似图形可能位于位似中心的两侧,也可能位于位似中心的同侧;
(3)位似中心只有一个.
知识点2 位似多边形的性质
1.位似多边形上任意一对对应点到位似中心的距离之比等于 .
2.位似多边形上对应点和位似中心在
3.位似多边形上的对应线段
4.位似多边形是特殊的相似图形,因此位似图形具有相似图形的 性质.
注意
可以应用性质1对图形进行放大(或缩小),使得放大(或缩小)前后的两个图形是位似图形.
知识点3 位似多边形的画法
1.画位似多边形的步骤:
(1)确定 O,在原图形上取关键点;
(2)以各 为端点,向点 O作射线(或以点O为端点向各关键点作射线);
(3)在射线上截取,找关键点的 ,并使其满足放缩比例;
(4)按原图形顺次 对应点,即可得到原图形放大或缩小后的图形.
2.位似图形的基本模式:
规律总结 (1)画位似图形的依据是位似图形的性质,关键是要准确地按比例画出各线段的长.
(2)在实际操作时,有的位似中心已知,有的位似中心需要依据实际情况来确定.
(3)位似中心可以在两个图形的同侧(称为外位似),也可以在两个图形之间(称为内位似);还可以在两个图的一条对应边上或一个对应顶点处.
明考点·识方法
考点1 位似图形的概念
典例1 下面每组图形中都有两个图形.
(1)哪一组中的两个图形是位似图形
(2)作出位似图形的位似中心.
规律总结
1.判断两个图形是不是位似图形应满足两个条件:①是相似图形.②两个图形每组对应点所在直线都经过同一点.两者缺一不可.
2.位似中心的确定:位似中心位于对应点连线所在的直线上,找出对应点连接是解题关键.
变式 下列图形不属于位似图形的是( )
考点2 位似图形的性质及应用
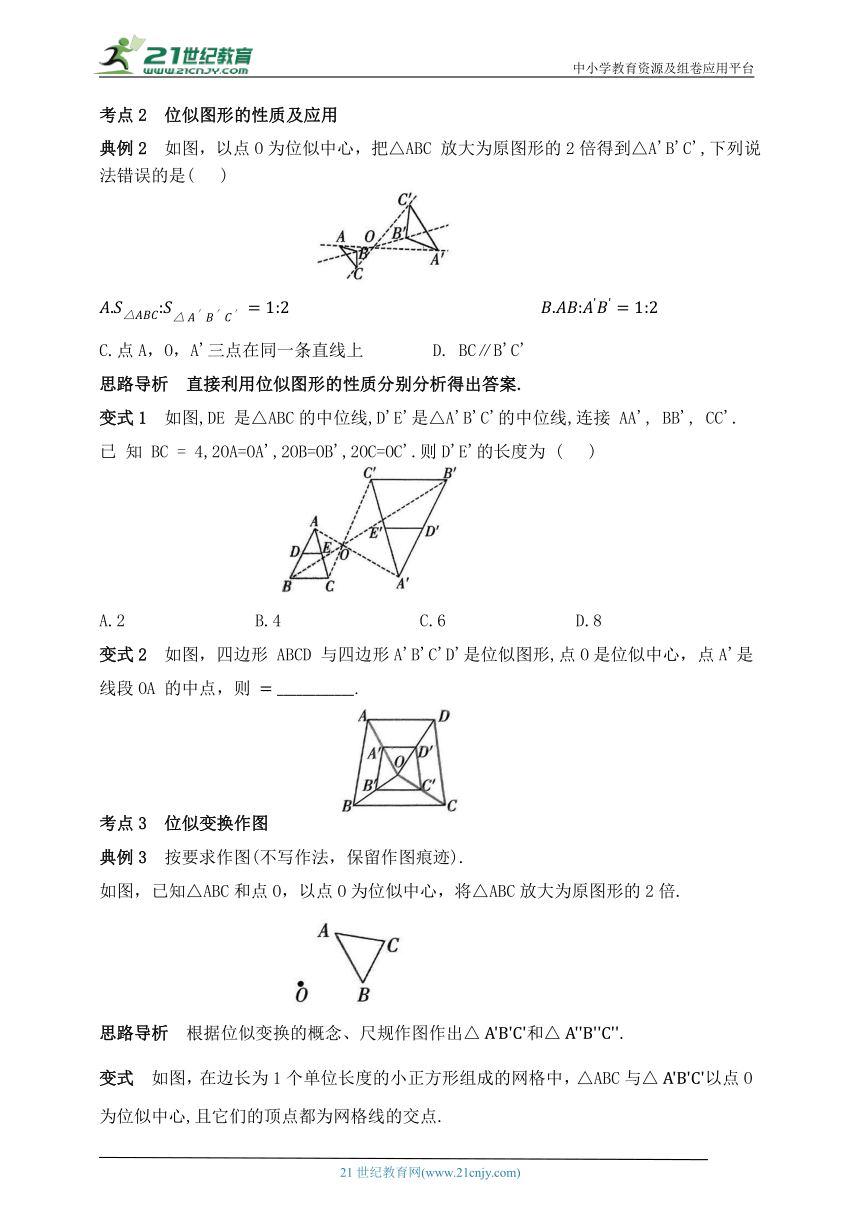
典例2 如图,以点O为位似中心,把△ABC 放大为原图形的2倍得到△A'B'C',下列说法错误的是( )
C.点A,O,A'三点在同一条直线上 D. BC∥B'C'
思路导析 直接利用位似图形的性质分别分析得出答案.
变式1 如图,DE 是△ABC的中位线,D'E'是△A'B'C'的中位线,连接 AA', BB', CC'. 已 知 BC = 4,2OA=OA',2OB=OB',2OC=OC'.则D'E'的长度为 ( )
A.2 B.4 C.6 D.8
变式2 如图,四边形 ABCD 与四边形A'B'C'D'是位似图形,点O是位似中心,点A'是线段OA 的中点,则 .
考点3 位似变换作图
典例3 按要求作图(不写作法,保留作图痕迹).
如图,已知△ABC和点O,以点O为位似中心,将△ABC放大为原图形的2倍.
思路导析 根据位似变换的概念、尺规作图作出和.
变式 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与以点O 为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点 O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是 ;
(2)请在此网格中,以点 C 为位似中心,再画一个,使它与△ABC 的位似比等于 2:1.
当堂测·夯基础
1.将△ABC的各边按如图所示的方式向外等距离扩 1 cm,得到△PNM,有以下结论:Ⅰ:△ABC与△PNM是相似三角形;Ⅱ:△ABC与△PNM是位似三角形.下列判断正确的是 ( )
A.Ⅰ正确,Ⅱ不正确 B.Ⅰ不正确,Ⅱ正确
C.Ⅰ,Ⅱ都正确 D.Ⅰ,Ⅱ都不正确
2.如图,在正方形网格中,△ABC的位似图形可以是 ( )
A.△BDE B.△FDE C.△DGF D.△BGF
3.如图,△ABC 和△DEF是以点O 为位似中心的位似图形,若OA: AD=4:5,△ABC 的面积为16,则△DEF的面积为 .
第3题图 第4题图
4.如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,点A 在线段 OA'上.若 OA: AA'=1: 2,则△ABC与△A'B'C'的周长之比为 .
5.如图,已知平行四边形 ABCD中,AE:EB=1:2.
(1)求 AE: DC的值;
(2)△AEF 与△CDF 是位似图形吗 若位似,请说明理由,并求出相似比;
(3)如果 求 S△CDF.
参考答案
【列清单·划重点】
知识点1 对应顶点 同一点 O k 相似比
知识点2 1.相似比 2.同一条直线上 3.平行或在同一条直线上 4.一切
知识点3 1.(1)位似中心 (2)关键点 (3)对应点 (4)连接
【明考点·识方法】
典例1 解:(1)是位似图形的有第①③⑤这3组;(2)位似中心O如图:
变式 B
典例2 A
变式1 B 变式2
典例3 解:如图:△A'B'C'和△A''B''C''即为所求:
变式 解:(1)如图所示:点O即为所求,△ABC与△A'B'C'的位似比是;1+2,
故答案为;112;
(2)如图所示:△A B C距为所求,
【当堂测·夯基础】
1. C 2. D 3. 81 4. 1:3
5.解:(1)∵平行四边形ABCD,∴DC=AB,
(2)位似.
∵平行四边形 ABCD,∴DC∥AB,∴∠DCF=∠EAF,∠FDC=∠FEA,
∴△AEF∽△CDF,且每组对应点连线相交于点 F,
∴△AEF 与△CDF是位似图形.∴相似比为
(3)∵△AEF∽△CDF,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.9.1 位似图形(学案含答案)
列清单·划重点
知识点1 位似多边形的概念
如果两个相似多边形任意一组 A,A'的连线都经过 ,且有( ·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O 叫做位似中心,k就是这两个相似多边形的
如图1,图2所示的图形都是位似图形,
注意
(1)位似图形是相似图形,是增加了条件的相似图形,这个条件就是:每组对应点所在直线都经过同一个点.而相似图形不一定是位似图形;
(2)两个位似图形可能位于位似中心的两侧,也可能位于位似中心的同侧;
(3)位似中心只有一个.
知识点2 位似多边形的性质
1.位似多边形上任意一对对应点到位似中心的距离之比等于 .
2.位似多边形上对应点和位似中心在
3.位似多边形上的对应线段
4.位似多边形是特殊的相似图形,因此位似图形具有相似图形的 性质.
注意
可以应用性质1对图形进行放大(或缩小),使得放大(或缩小)前后的两个图形是位似图形.
知识点3 位似多边形的画法
1.画位似多边形的步骤:
(1)确定 O,在原图形上取关键点;
(2)以各 为端点,向点 O作射线(或以点O为端点向各关键点作射线);
(3)在射线上截取,找关键点的 ,并使其满足放缩比例;
(4)按原图形顺次 对应点,即可得到原图形放大或缩小后的图形.
2.位似图形的基本模式:
规律总结 (1)画位似图形的依据是位似图形的性质,关键是要准确地按比例画出各线段的长.
(2)在实际操作时,有的位似中心已知,有的位似中心需要依据实际情况来确定.
(3)位似中心可以在两个图形的同侧(称为外位似),也可以在两个图形之间(称为内位似);还可以在两个图的一条对应边上或一个对应顶点处.
明考点·识方法
考点1 位似图形的概念
典例1 下面每组图形中都有两个图形.
(1)哪一组中的两个图形是位似图形
(2)作出位似图形的位似中心.
规律总结
1.判断两个图形是不是位似图形应满足两个条件:①是相似图形.②两个图形每组对应点所在直线都经过同一点.两者缺一不可.
2.位似中心的确定:位似中心位于对应点连线所在的直线上,找出对应点连接是解题关键.
变式 下列图形不属于位似图形的是( )
考点2 位似图形的性质及应用
典例2 如图,以点O为位似中心,把△ABC 放大为原图形的2倍得到△A'B'C',下列说法错误的是( )
C.点A,O,A'三点在同一条直线上 D. BC∥B'C'
思路导析 直接利用位似图形的性质分别分析得出答案.
变式1 如图,DE 是△ABC的中位线,D'E'是△A'B'C'的中位线,连接 AA', BB', CC'. 已 知 BC = 4,2OA=OA',2OB=OB',2OC=OC'.则D'E'的长度为 ( )
A.2 B.4 C.6 D.8
变式2 如图,四边形 ABCD 与四边形A'B'C'D'是位似图形,点O是位似中心,点A'是线段OA 的中点,则 .
考点3 位似变换作图
典例3 按要求作图(不写作法,保留作图痕迹).
如图,已知△ABC和点O,以点O为位似中心,将△ABC放大为原图形的2倍.
思路导析 根据位似变换的概念、尺规作图作出和.
变式 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与以点O 为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点 O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是 ;
(2)请在此网格中,以点 C 为位似中心,再画一个,使它与△ABC 的位似比等于 2:1.
当堂测·夯基础
1.将△ABC的各边按如图所示的方式向外等距离扩 1 cm,得到△PNM,有以下结论:Ⅰ:△ABC与△PNM是相似三角形;Ⅱ:△ABC与△PNM是位似三角形.下列判断正确的是 ( )
A.Ⅰ正确,Ⅱ不正确 B.Ⅰ不正确,Ⅱ正确
C.Ⅰ,Ⅱ都正确 D.Ⅰ,Ⅱ都不正确
2.如图,在正方形网格中,△ABC的位似图形可以是 ( )
A.△BDE B.△FDE C.△DGF D.△BGF
3.如图,△ABC 和△DEF是以点O 为位似中心的位似图形,若OA: AD=4:5,△ABC 的面积为16,则△DEF的面积为 .
第3题图 第4题图
4.如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,点A 在线段 OA'上.若 OA: AA'=1: 2,则△ABC与△A'B'C'的周长之比为 .
5.如图,已知平行四边形 ABCD中,AE:EB=1:2.
(1)求 AE: DC的值;
(2)△AEF 与△CDF 是位似图形吗 若位似,请说明理由,并求出相似比;
(3)如果 求 S△CDF.
参考答案
【列清单·划重点】
知识点1 对应顶点 同一点 O k 相似比
知识点2 1.相似比 2.同一条直线上 3.平行或在同一条直线上 4.一切
知识点3 1.(1)位似中心 (2)关键点 (3)对应点 (4)连接
【明考点·识方法】
典例1 解:(1)是位似图形的有第①③⑤这3组;(2)位似中心O如图:
变式 B
典例2 A
变式1 B 变式2
典例3 解:如图:△A'B'C'和△A''B''C''即为所求:
变式 解:(1)如图所示:点O即为所求,△ABC与△A'B'C'的位似比是;1+2,
故答案为;112;
(2)如图所示:△A B C距为所求,
【当堂测·夯基础】
1. C 2. D 3. 81 4. 1:3
5.解:(1)∵平行四边形ABCD,∴DC=AB,
(2)位似.
∵平行四边形 ABCD,∴DC∥AB,∴∠DCF=∠EAF,∠FDC=∠FEA,
∴△AEF∽△CDF,且每组对应点连线相交于点 F,
∴△AEF 与△CDF是位似图形.∴相似比为
(3)∵△AEF∽△CDF,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
