人教版高中物理选择性必修第一册3动量守恒在几类模型中的应用课件(共46张PPT)
文档属性
| 名称 | 人教版高中物理选择性必修第一册3动量守恒在几类模型中的应用课件(共46张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-03-19 00:00:00 | ||
图片预览











文档简介
(共46张PPT)
第一章 动量守恒定律
动量守恒在几类模型中的应用
学习目标
1、会用动量守恒和能量观点分析计算子弹打木块模型。
2、会用动量守恒和能量观点分析计算滑块—木板模型。
3、会用动量守恒处理爆炸、反冲和人船模型
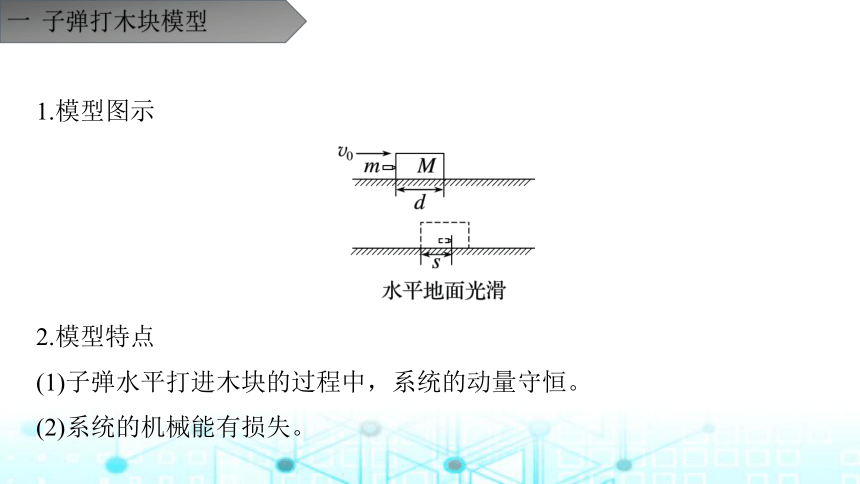
1.模型图示
2.模型特点
(1)子弹水平打进木块的过程中,系统的动量守恒。
(2)系统的机械能有损失。
3.两种情景
(1)子弹嵌入木块中,两者速度相等,机械能损失最多(完全非弹性碰撞)
动量守恒:mv0=(m+M)v
(2)子弹穿透木块
动量守恒:mv0=mv1+Mv2
例1 如图所示,在光滑的水平桌面上静止放置一个质量为980 g的长方形匀质木块,现有一质量为20 g的子弹以大小为300 m/s的水平速度沿木块的中心轴线射向木块,最终留在木块中没有射出,和木块一起以共同的速度运动。已知木块沿子弹运动方向的长度为10 cm,子弹打进木块的深度为6 cm。设木块对子弹的阻力保持不变。
(1)求子弹和木块的共同速度以及它们在此过程中
所产生的内能。
答案 6 m/s 882 J
设子弹射入木块后与木块的共同速度为v,对子弹和木块组成的系统,由动量守恒定律得mv0=(M+m)v,代入数据解得v=6 m/s
此过程系统所产生的内能
(2)若子弹是以大小为400 m/s的水平速度从同一方向水平射向该木块,则在射中木块后能否射穿该木块?
答案 能
假设子弹以v0′=400 m/s的速度入射时没有射穿木块,则对以子弹和木块组成的系统,由动量守恒定律得mv0′=(M+m)v′
解得v′=8 m/s
此过程系统损失的机械能为
由功能关系有Q=ΔE=F阻x相=F阻d
ΔE′=F阻x相′=F阻d′
因为d′>10 cm,所以能射穿木块。
拓展 在例1中,若子弹能射出木块,则:
(1)(多选)当子弹射入的速度增大时,下列说法正确的是
A.木块最终获得的动能变大
B.子弹损失的动能变大
C.子弹穿过木块的时间变短
D.木块在被击穿过程中的位移变小
√
√
子弹的入射速度越大,子弹击穿木块所用的时间越短,木块相对地面的位移越小,但子弹相对木块的位移不变,C、D正确;
木块动能的增加量ΔEk=Ffx,木块对子弹的阻力恒定,由上述分析可知木块动能的增加量变小,即木块最终获得的动能变小,子弹损失的动能也变小,A、B错误。
(2)在木块固定和不固定的两种情况下,以下说法正确的是
A.若木块固定,则子弹对木块的摩擦力的冲量为零
B.若木块不固定,则子弹减小的动能等于木块增加的动能
C.不论木块是否固定,两种情况下木块对子弹的摩擦力的冲量大小相等
D.不论木块是否固定,两种情况下子弹与木块间因摩擦产生的热量相等
√
若木块固定,子弹在木块中运动的时间t不为零,摩擦力Ff不为零,则子弹对木块的摩擦力的冲量I=Fft不为零,A错误;
若木块不固定,子弹减小的动能等于木块增加的动能与系统增加的内能之和,可知子弹减小的动能大于木块增加的动能,B错误;
木块固定时子弹射出木块所用时间较短,木块不固定时子弹射出木块所用时间较长,摩擦力大小不变,则木块不固定时木块对子弹的摩擦力的冲量大小大于木块固定时木块对子弹的摩擦力的冲量大小,C错误;
不论木块是否固定,因摩擦产生的热量等于摩擦力与木块长度的乘积,摩擦力与木块长度都不变,因此两种情况下子弹与木块间因摩擦产生的热量相等,D正确。
1.模型图示
2.模型特点
(1)系统的动量守恒,但机械能不守恒,摩擦力与两者相对位移的乘积等于系统减少的机械能。
(2)若滑块未从木板上滑下,当两者速度相同时,木板速度最大,相对位移最大。
3.求解方法
(1)求速度:根据动量守恒定律求解,研究对象为一个系统;
(2)求时间:根据动量定理求解,研究对象为一个物体;
(3)求系统产生的内能或相对位移:根据能量守恒定律Q=FfΔx或Q=E初-E末,研究对象为一个系统。
例2 质量m1=0.3 kg的小车静止在光滑的水平面上,车长L=1.5 m,现有一质量为m2=0.2 kg、可视为质点的物块,以水平向右的速度v0=2 m/s从左端滑上小车,如图所示,最后在小车上某处与小车保持相对静止,物块与小车间的动摩擦因数μ=0.5,g取10 m/s2,求:
(1)物块与小车的共同速度大小v;
答案 0.8 m/s
设物块与小车的共同速度为v,以水平向右为正
方向,根据动量守恒定律有m2v0=(m1+m2)v,
解得v= =0.8 m/s
(2)物块相对小车滑行的时间t;
答案 0.24 s
对物块由动量定理有-μm2gt=m2v-m2v0
(3)从开始到共速,小车运动的位移大小x1;
答案 0.096 m
(4)从开始到共速,物块运动的位移大小x2;
答案 0.336 m
方法一 Δx=x2-x1=0.24 m
Q=μm2g·Δx=0.24 J
(5)在此过程中系统产生的内能;
答案 0.24 J
m2v0′=(m1+m2)v′
(6)若物块不滑离小车,物块的速度不能超过多少。
答案 5 m/s
联立解得v0′=5 m/s。
拓展 在例2中,若增大物块与小车间的动摩擦因数,则因摩擦产生的内能将_____(填“增大”“减小”或“不变”)。
例3 如图所示,光滑水平面上有一平板车B,其上表面水平,质量mB=
1 kg,在其左端放置一物块A,质量mA=0.4 kg。开始A、B均处于静止状态,玩具手枪里面有一颗质量为m0=100 g的子弹以初速度v0=100 m/s水平射向A,子弹瞬间射入并留在物块中,最终物块A及子弹相对地面以16 m/s的速度滑离平板车,已知A、B间的动摩擦因数μ=0.8,
g取10 m/s2。求:
(1)子弹射入物块A的过程中物块对子弹的冲量;
答案 8 N·s,方向水平向左
子弹射入物块A的过程,由动量守恒定律得m0v0=(m0+mA)v1
解得子弹与物块A的共同速度大小为v1=20 m/s
对子弹由动量定理得I=m0v1-m0v0=-8 N·s
所以子弹射入物块A的过程中物块对子弹的冲量大小为8 N·s,方向水平向左。
(3)物块A在平板车上滑行的时间t;
答案 0.5 s
对物块A与子弹由动量定理得
-μ(m0+mA)gt=(m0+mA)v2-(m0+mA)v1
解得物块A在平板车上滑行的时间t=0.5 s
(4)求平板车的长度L。
答案 8.5 m
思考 子弹打木块模型、滑块—木板模型有什么区别与联系?
答案 这两个模型中,子弹打木块模型是一个物体从另外一个物体内部穿行,时间较短,在滑块—木板模型中,是一个物体在另外一个物体表面滑行,时间相对较长,在运动过程中都受到阻力作用,运动规律相同。
返回
考向1 “爆炸”问题
爆炸现象的三个规律
动量守恒 由于爆炸是在极短的时间内完成的,爆炸物体间的相互作用力远远大于
受到的外力,所以在爆炸过程中,系统的总动量守恒
动能增加 在爆炸过程中,由于有其他形式的能量(如化学能)转化为动能,所以爆
炸后系统的总动能增加
位置不变 爆炸的时间极短,因而作用过程中,物体产生的位移很小,一般可忽略不计,
可以认为爆炸后仍然从爆炸前的位置以新的动量开始运动
(2)炸药的化学能有多少转化为机械能?
考向2 反冲模型
D
对反冲运动的三点说明
作用原理 反冲运动是系统内物体之间的作用力和反作用力产生的效果
动量守恒 反冲运动中系统不受外力或内力远大于外力,所以反冲运动遵循
动量守恒定律
机械能增加 反冲运动中,由于有其他形式的能转化为机械能,所以系统的总
机械能增加
考向3 反冲运动中的“人船”模型
B
(1)若固定小车,求滑块运动过程中对小车的最大压力。
第一章 动量守恒定律
动量守恒在几类模型中的应用
学习目标
1、会用动量守恒和能量观点分析计算子弹打木块模型。
2、会用动量守恒和能量观点分析计算滑块—木板模型。
3、会用动量守恒处理爆炸、反冲和人船模型
1.模型图示
2.模型特点
(1)子弹水平打进木块的过程中,系统的动量守恒。
(2)系统的机械能有损失。
3.两种情景
(1)子弹嵌入木块中,两者速度相等,机械能损失最多(完全非弹性碰撞)
动量守恒:mv0=(m+M)v
(2)子弹穿透木块
动量守恒:mv0=mv1+Mv2
例1 如图所示,在光滑的水平桌面上静止放置一个质量为980 g的长方形匀质木块,现有一质量为20 g的子弹以大小为300 m/s的水平速度沿木块的中心轴线射向木块,最终留在木块中没有射出,和木块一起以共同的速度运动。已知木块沿子弹运动方向的长度为10 cm,子弹打进木块的深度为6 cm。设木块对子弹的阻力保持不变。
(1)求子弹和木块的共同速度以及它们在此过程中
所产生的内能。
答案 6 m/s 882 J
设子弹射入木块后与木块的共同速度为v,对子弹和木块组成的系统,由动量守恒定律得mv0=(M+m)v,代入数据解得v=6 m/s
此过程系统所产生的内能
(2)若子弹是以大小为400 m/s的水平速度从同一方向水平射向该木块,则在射中木块后能否射穿该木块?
答案 能
假设子弹以v0′=400 m/s的速度入射时没有射穿木块,则对以子弹和木块组成的系统,由动量守恒定律得mv0′=(M+m)v′
解得v′=8 m/s
此过程系统损失的机械能为
由功能关系有Q=ΔE=F阻x相=F阻d
ΔE′=F阻x相′=F阻d′
因为d′>10 cm,所以能射穿木块。
拓展 在例1中,若子弹能射出木块,则:
(1)(多选)当子弹射入的速度增大时,下列说法正确的是
A.木块最终获得的动能变大
B.子弹损失的动能变大
C.子弹穿过木块的时间变短
D.木块在被击穿过程中的位移变小
√
√
子弹的入射速度越大,子弹击穿木块所用的时间越短,木块相对地面的位移越小,但子弹相对木块的位移不变,C、D正确;
木块动能的增加量ΔEk=Ffx,木块对子弹的阻力恒定,由上述分析可知木块动能的增加量变小,即木块最终获得的动能变小,子弹损失的动能也变小,A、B错误。
(2)在木块固定和不固定的两种情况下,以下说法正确的是
A.若木块固定,则子弹对木块的摩擦力的冲量为零
B.若木块不固定,则子弹减小的动能等于木块增加的动能
C.不论木块是否固定,两种情况下木块对子弹的摩擦力的冲量大小相等
D.不论木块是否固定,两种情况下子弹与木块间因摩擦产生的热量相等
√
若木块固定,子弹在木块中运动的时间t不为零,摩擦力Ff不为零,则子弹对木块的摩擦力的冲量I=Fft不为零,A错误;
若木块不固定,子弹减小的动能等于木块增加的动能与系统增加的内能之和,可知子弹减小的动能大于木块增加的动能,B错误;
木块固定时子弹射出木块所用时间较短,木块不固定时子弹射出木块所用时间较长,摩擦力大小不变,则木块不固定时木块对子弹的摩擦力的冲量大小大于木块固定时木块对子弹的摩擦力的冲量大小,C错误;
不论木块是否固定,因摩擦产生的热量等于摩擦力与木块长度的乘积,摩擦力与木块长度都不变,因此两种情况下子弹与木块间因摩擦产生的热量相等,D正确。
1.模型图示
2.模型特点
(1)系统的动量守恒,但机械能不守恒,摩擦力与两者相对位移的乘积等于系统减少的机械能。
(2)若滑块未从木板上滑下,当两者速度相同时,木板速度最大,相对位移最大。
3.求解方法
(1)求速度:根据动量守恒定律求解,研究对象为一个系统;
(2)求时间:根据动量定理求解,研究对象为一个物体;
(3)求系统产生的内能或相对位移:根据能量守恒定律Q=FfΔx或Q=E初-E末,研究对象为一个系统。
例2 质量m1=0.3 kg的小车静止在光滑的水平面上,车长L=1.5 m,现有一质量为m2=0.2 kg、可视为质点的物块,以水平向右的速度v0=2 m/s从左端滑上小车,如图所示,最后在小车上某处与小车保持相对静止,物块与小车间的动摩擦因数μ=0.5,g取10 m/s2,求:
(1)物块与小车的共同速度大小v;
答案 0.8 m/s
设物块与小车的共同速度为v,以水平向右为正
方向,根据动量守恒定律有m2v0=(m1+m2)v,
解得v= =0.8 m/s
(2)物块相对小车滑行的时间t;
答案 0.24 s
对物块由动量定理有-μm2gt=m2v-m2v0
(3)从开始到共速,小车运动的位移大小x1;
答案 0.096 m
(4)从开始到共速,物块运动的位移大小x2;
答案 0.336 m
方法一 Δx=x2-x1=0.24 m
Q=μm2g·Δx=0.24 J
(5)在此过程中系统产生的内能;
答案 0.24 J
m2v0′=(m1+m2)v′
(6)若物块不滑离小车,物块的速度不能超过多少。
答案 5 m/s
联立解得v0′=5 m/s。
拓展 在例2中,若增大物块与小车间的动摩擦因数,则因摩擦产生的内能将_____(填“增大”“减小”或“不变”)。
例3 如图所示,光滑水平面上有一平板车B,其上表面水平,质量mB=
1 kg,在其左端放置一物块A,质量mA=0.4 kg。开始A、B均处于静止状态,玩具手枪里面有一颗质量为m0=100 g的子弹以初速度v0=100 m/s水平射向A,子弹瞬间射入并留在物块中,最终物块A及子弹相对地面以16 m/s的速度滑离平板车,已知A、B间的动摩擦因数μ=0.8,
g取10 m/s2。求:
(1)子弹射入物块A的过程中物块对子弹的冲量;
答案 8 N·s,方向水平向左
子弹射入物块A的过程,由动量守恒定律得m0v0=(m0+mA)v1
解得子弹与物块A的共同速度大小为v1=20 m/s
对子弹由动量定理得I=m0v1-m0v0=-8 N·s
所以子弹射入物块A的过程中物块对子弹的冲量大小为8 N·s,方向水平向左。
(3)物块A在平板车上滑行的时间t;
答案 0.5 s
对物块A与子弹由动量定理得
-μ(m0+mA)gt=(m0+mA)v2-(m0+mA)v1
解得物块A在平板车上滑行的时间t=0.5 s
(4)求平板车的长度L。
答案 8.5 m
思考 子弹打木块模型、滑块—木板模型有什么区别与联系?
答案 这两个模型中,子弹打木块模型是一个物体从另外一个物体内部穿行,时间较短,在滑块—木板模型中,是一个物体在另外一个物体表面滑行,时间相对较长,在运动过程中都受到阻力作用,运动规律相同。
返回
考向1 “爆炸”问题
爆炸现象的三个规律
动量守恒 由于爆炸是在极短的时间内完成的,爆炸物体间的相互作用力远远大于
受到的外力,所以在爆炸过程中,系统的总动量守恒
动能增加 在爆炸过程中,由于有其他形式的能量(如化学能)转化为动能,所以爆
炸后系统的总动能增加
位置不变 爆炸的时间极短,因而作用过程中,物体产生的位移很小,一般可忽略不计,
可以认为爆炸后仍然从爆炸前的位置以新的动量开始运动
(2)炸药的化学能有多少转化为机械能?
考向2 反冲模型
D
对反冲运动的三点说明
作用原理 反冲运动是系统内物体之间的作用力和反作用力产生的效果
动量守恒 反冲运动中系统不受外力或内力远大于外力,所以反冲运动遵循
动量守恒定律
机械能增加 反冲运动中,由于有其他形式的能转化为机械能,所以系统的总
机械能增加
考向3 反冲运动中的“人船”模型
B
(1)若固定小车,求滑块运动过程中对小车的最大压力。
