人教版 九年级数学下册 27.3 位似 课时练习题(含答案)
文档属性
| 名称 | 人教版 九年级数学下册 27.3 位似 课时练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 737.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 00:00:00 | ||
图片预览



文档简介
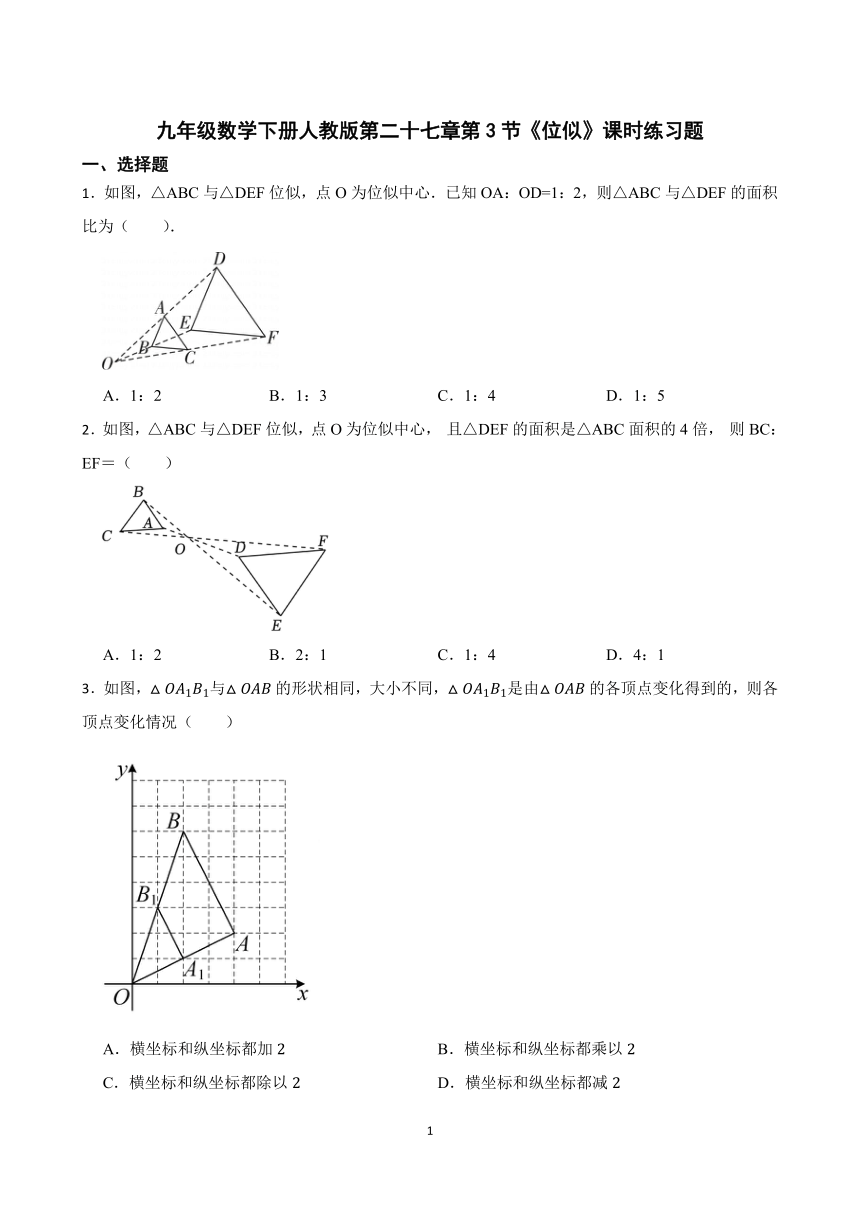
九年级数学下册人教版第二十七章第3节《位似》课时练习题
一、选择题
1.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).
A.1:2 B.1:3 C.1:4 D.1:5
2.如图,△ABC与△DEF位似,点O为位似中心, 且△DEF的面积是△ABC面积的4倍, 则BC:EF=( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,与的形状相同,大小不同,是由的各顶点变化得到的,则各顶点变化情况( )
A.横坐标和纵坐标都加 B.横坐标和纵坐标都乘以
C.横坐标和纵坐标都除以 D.横坐标和纵坐标都减
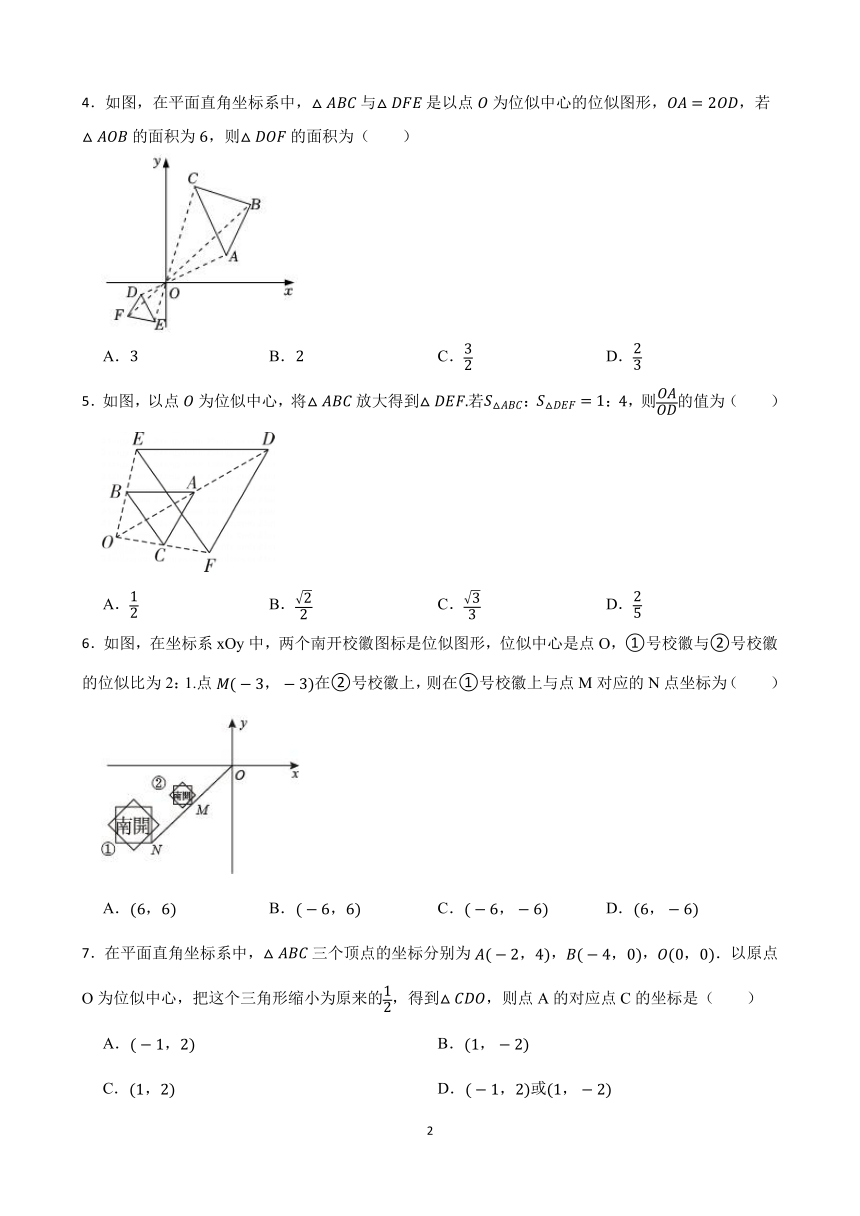
4.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,,若的面积为,则的面积为( )
A. B. C. D.
5.如图,以点为位似中心,将放大得到若::,则的值为( )
A. B. C. D.
6.如图,在坐标系xOy中,两个南开校徽图标是位似图形,位似中心是点O,①号校徽与②号校徽的位似比为2:1.点在②号校徽上,则在①号校徽上与点M对应的N点坐标为( )
A. B. C. D.
7.在平面直角坐标系中,三个顶点的坐标分别为,,.以原点O为位似中心,把这个三角形缩小为原来的,得到,则点A的对应点C的坐标是( )
A. B.
C. D.或
8.如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的异侧画 ,使 与 成位似图形,且相似比为 ,则线段DF的长度为( )
A. B.2 C. D.4
9.如图,已知与位似,位似中心为O,且的面积与的面积之比是16:9,则AO:AD的值为( ).
A.4:7 B.4:3 C.6:4 D.9:5
10.如图所示,在平面直角坐标系中,△OAB的顶点为.以点为位似中心,在第三象限内作与的位似比为的位似图形,则点的坐标是( ).
A. B. C. D.
二、填空题
11.如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为
12.如图,在平面直角坐标系中,四边形的顶点坐标分别是,若四边形与四边形关于原点位似,且四边形的面积是四边形面积的4倍,则第一象限内点的坐标为 .
13.如图,四边形ABCD与四边形EFGH位似,位似中心是点O.若,则=
14.如图所示,点是四边形ABCD内一点,分别是OA,OB,OC,OD上的点,且,若四边形的面积为,则四边形ABCD的面积为 .
15.如图,在平面直角坐标系中,等腰直角是等腰直角以原点为位似中心的位似图形,且位似比为:,点,,在,则点坐标为 .
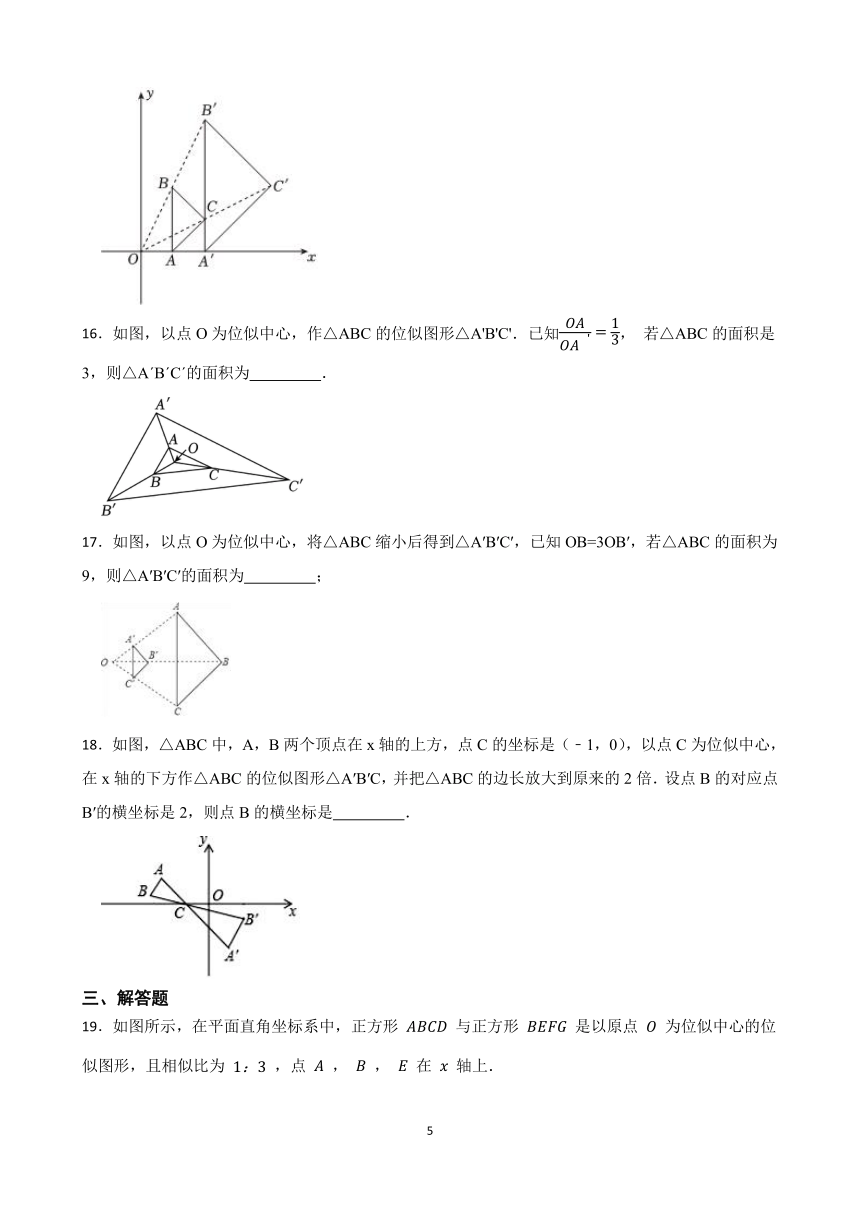
16.如图,以点O为位似中心,作△ABC的位似图形△A'B'C'.已知, 若△ABC的面积是3,则△A B C 的面积为 .
17.如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,若△ABC的面积为9,则△A′B′C′的面积为 ;
18.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .
三、解答题
19.如图所示,在平面直角坐标系中,正方形 与正方形 是以原点 为位似中心的位似图形,且相似比为 ,点 , , 在 轴上.
(1)若点 的坐标为 ,直接写出点 和点 的坐标;
(2)若正方形 的边长为 ,求点 的坐标.
20.如图,在平面直角坐标系中,的顶点均在网格格点上,且点A、B、C的坐标分别为,,.
(1)以点O为位似中心,在第一象限画出的位似图形,使与的相似比为2:1;
(2)在(1)的条件下,分别写出点B、C的对应点、的坐标.
21.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
22.如图,在平面直角坐标系中,已知线段与线段关于原点中心对称,点是点的对应点,点是点的对应点.
⑴画出线段和;
⑵画出线段以点为位似中心,位似比为的线段.
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
24.如图,每个正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)请在方格中确定位似中心O的位置,并以O为坐标原点,以网格线所在的直线为坐标轴建立平面直角坐标系.
(2)△ABC与△A1B1C1的位似比 .
(3)在图中作出△ABC关于原点O成中心对称的图形△A2B2C2.
25.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
26.在如图的方格纸中,的顶点坐标分别为,,,与是关于点P为位似中心的位似图形.
( 1 )在图中标出位似中心P的位置并直接写出点P的坐标为 .
( 2 )以原点O为位似中心,在位似中心的同侧画出的一个位似,使它与的位似比为2:1;
( 3 )的内部一点M的坐标为,直接写出点M在中的对应点的坐标为 .
27.放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,,,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接,,可证得以下结论:
①和为等腰三角形,则,(180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
答案
1-10 CACBA CDAAB
11.4:9
12.
13.
14.
15.(8,4)
16.27
17.1
18.-2.5
19.(1)解:C点坐标为 , 点坐标为
(2)解:∵正方形 与正方形 是以原点 为位似中心的位似图形,
∴正方形 的边长为 ,则正方形 的边长为 , ,
∴ : ,解得 ,
∴点 的坐标为
20.(1)解: 如图所示.
(2)解:由(1)中的图形可知 、
21.(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
22.解:⑴如图,线段和即为所求作的线段.
⑵如图,线段即为所求作的线段.
23.(1)解:如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2)
(2)解:如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4)
(3)解:如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
24.(1)解:如图所示,点O即为所求;
(2)△ABC与△A1B1C1的位似比= =2:1, 故答案为:2:1
(3)如图所示,△A2B2C2即为所求
25.解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
26.解:⑴如图,点P为所作;
故答案为:;
⑵如图,为所作;
⑶.
27.解:连接,,如图,
①∵,
∴
∴△OAD和△OEC是等腰三角形,
∴∠,∠
∴∠,∠
②∵,
∴四边形为平行四边形(两组对边分别相等的四边形是平行四边形)
③∵
∴,,三点在一条直线上;
④∵图形M和图形N是以点O为位似中心的位似图形,
∴其倍数比为三角形的边长比即:,
又,且
∴
即:当时,图形N是以点O为位似中心,把图形M放大为原来的倍得到的.
故答案为:;两组对边分别相等的四边形是平行四边形;
一、选择题
1.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).
A.1:2 B.1:3 C.1:4 D.1:5
2.如图,△ABC与△DEF位似,点O为位似中心, 且△DEF的面积是△ABC面积的4倍, 则BC:EF=( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,与的形状相同,大小不同,是由的各顶点变化得到的,则各顶点变化情况( )
A.横坐标和纵坐标都加 B.横坐标和纵坐标都乘以
C.横坐标和纵坐标都除以 D.横坐标和纵坐标都减
4.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,,若的面积为,则的面积为( )
A. B. C. D.
5.如图,以点为位似中心,将放大得到若::,则的值为( )
A. B. C. D.
6.如图,在坐标系xOy中,两个南开校徽图标是位似图形,位似中心是点O,①号校徽与②号校徽的位似比为2:1.点在②号校徽上,则在①号校徽上与点M对应的N点坐标为( )
A. B. C. D.
7.在平面直角坐标系中,三个顶点的坐标分别为,,.以原点O为位似中心,把这个三角形缩小为原来的,得到,则点A的对应点C的坐标是( )
A. B.
C. D.或
8.如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的异侧画 ,使 与 成位似图形,且相似比为 ,则线段DF的长度为( )
A. B.2 C. D.4
9.如图,已知与位似,位似中心为O,且的面积与的面积之比是16:9,则AO:AD的值为( ).
A.4:7 B.4:3 C.6:4 D.9:5
10.如图所示,在平面直角坐标系中,△OAB的顶点为.以点为位似中心,在第三象限内作与的位似比为的位似图形,则点的坐标是( ).
A. B. C. D.
二、填空题
11.如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为
12.如图,在平面直角坐标系中,四边形的顶点坐标分别是,若四边形与四边形关于原点位似,且四边形的面积是四边形面积的4倍,则第一象限内点的坐标为 .
13.如图,四边形ABCD与四边形EFGH位似,位似中心是点O.若,则=
14.如图所示,点是四边形ABCD内一点,分别是OA,OB,OC,OD上的点,且,若四边形的面积为,则四边形ABCD的面积为 .
15.如图,在平面直角坐标系中,等腰直角是等腰直角以原点为位似中心的位似图形,且位似比为:,点,,在,则点坐标为 .
16.如图,以点O为位似中心,作△ABC的位似图形△A'B'C'.已知, 若△ABC的面积是3,则△A B C 的面积为 .
17.如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,若△ABC的面积为9,则△A′B′C′的面积为 ;
18.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .
三、解答题
19.如图所示,在平面直角坐标系中,正方形 与正方形 是以原点 为位似中心的位似图形,且相似比为 ,点 , , 在 轴上.
(1)若点 的坐标为 ,直接写出点 和点 的坐标;
(2)若正方形 的边长为 ,求点 的坐标.
20.如图,在平面直角坐标系中,的顶点均在网格格点上,且点A、B、C的坐标分别为,,.
(1)以点O为位似中心,在第一象限画出的位似图形,使与的相似比为2:1;
(2)在(1)的条件下,分别写出点B、C的对应点、的坐标.
21.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
22.如图,在平面直角坐标系中,已知线段与线段关于原点中心对称,点是点的对应点,点是点的对应点.
⑴画出线段和;
⑵画出线段以点为位似中心,位似比为的线段.
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
24.如图,每个正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)请在方格中确定位似中心O的位置,并以O为坐标原点,以网格线所在的直线为坐标轴建立平面直角坐标系.
(2)△ABC与△A1B1C1的位似比 .
(3)在图中作出△ABC关于原点O成中心对称的图形△A2B2C2.
25.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
26.在如图的方格纸中,的顶点坐标分别为,,,与是关于点P为位似中心的位似图形.
( 1 )在图中标出位似中心P的位置并直接写出点P的坐标为 .
( 2 )以原点O为位似中心,在位似中心的同侧画出的一个位似,使它与的位似比为2:1;
( 3 )的内部一点M的坐标为,直接写出点M在中的对应点的坐标为 .
27.放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,,,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接,,可证得以下结论:
①和为等腰三角形,则,(180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
答案
1-10 CACBA CDAAB
11.4:9
12.
13.
14.
15.(8,4)
16.27
17.1
18.-2.5
19.(1)解:C点坐标为 , 点坐标为
(2)解:∵正方形 与正方形 是以原点 为位似中心的位似图形,
∴正方形 的边长为 ,则正方形 的边长为 , ,
∴ : ,解得 ,
∴点 的坐标为
20.(1)解: 如图所示.
(2)解:由(1)中的图形可知 、
21.(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
22.解:⑴如图,线段和即为所求作的线段.
⑵如图,线段即为所求作的线段.
23.(1)解:如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2)
(2)解:如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4)
(3)解:如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
24.(1)解:如图所示,点O即为所求;
(2)△ABC与△A1B1C1的位似比= =2:1, 故答案为:2:1
(3)如图所示,△A2B2C2即为所求
25.解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
26.解:⑴如图,点P为所作;
故答案为:;
⑵如图,为所作;
⑶.
27.解:连接,,如图,
①∵,
∴
∴△OAD和△OEC是等腰三角形,
∴∠,∠
∴∠,∠
②∵,
∴四边形为平行四边形(两组对边分别相等的四边形是平行四边形)
③∵
∴,,三点在一条直线上;
④∵图形M和图形N是以点O为位似中心的位似图形,
∴其倍数比为三角形的边长比即:,
又,且
∴
即:当时,图形N是以点O为位似中心,把图形M放大为原来的倍得到的.
故答案为:;两组对边分别相等的四边形是平行四边形;
