2025年浙江省中考数学一轮复习专题检测 专题11 一次函数的应用与综合问题(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题11 一次函数的应用与综合问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 12:45:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题11 一次函数的应用与综合问题
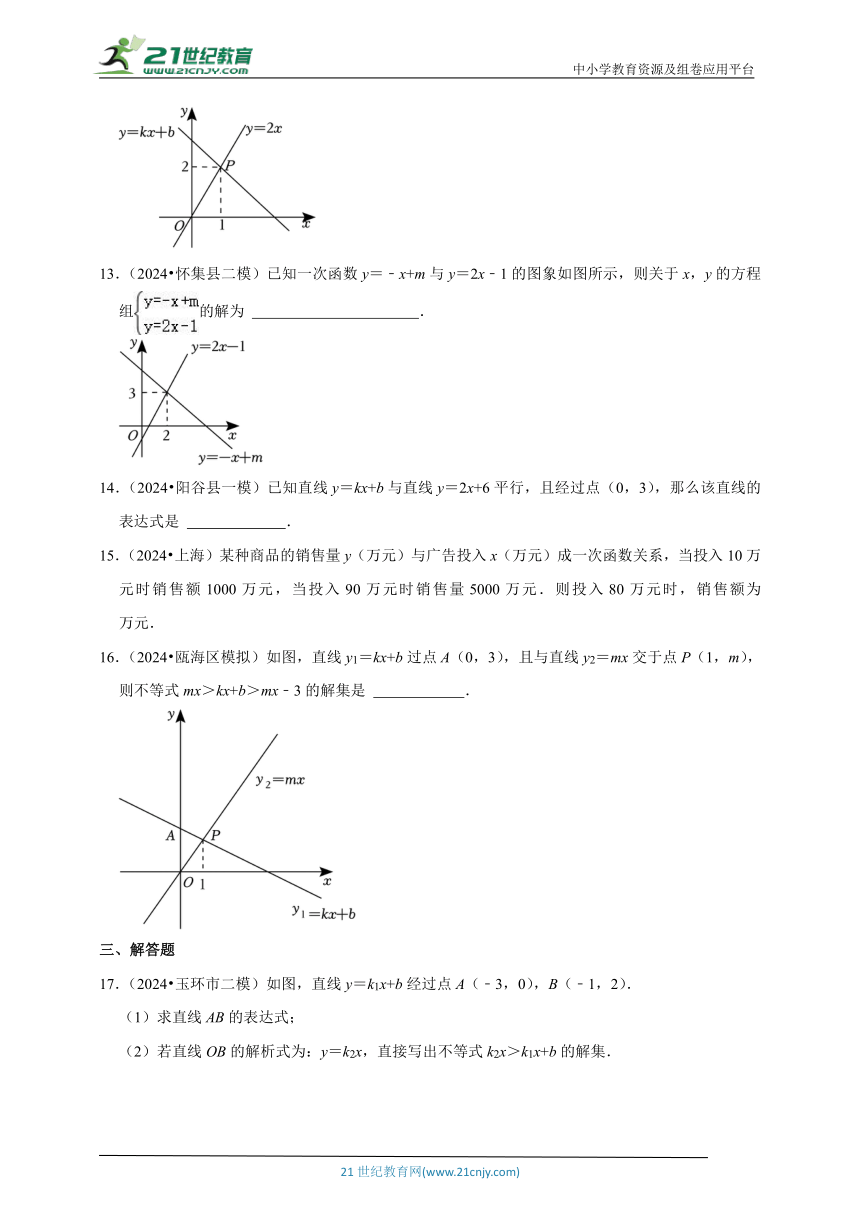
一、选择题
1.(2024 阎良区二模)如图,已知直线y=kx+b(k、b为常数,k≠0),则关于x的方程kx+b=1的解是x=( )
A.﹣4 B.﹣1 C.0 D.﹣2
2.(2023 南海区一模)某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )
A.y=20x B.y=40﹣2x C. D.y=x(40﹣2x)
3.(2024 庄浪县二模)如图,一次函数y=kx+2(k为常数且k≠0)和y=3x+1的图象相交于点A,根据图象可知关于x的方程kx+2=3x+1的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
4.(2024 昭阳区模拟)如图,直线y=ax+b(a≠0)过点A(0,2),B(3,0),则不等式ax+b>0的解集是( )
A.x>3 B.x<3 C.x>2 D.x<2
5.(2024 秦都区二模)如图是一次函数y1=kx﹣2k与y2=x+a的图象,则下列选项正确的是( )
A.k>0
B.a>0
C.当x<2时,一次函数 y1=kx﹣2k的值都为负数
D.方程kx﹣2k=x+a的解是x=3
6.(2024 揭阳一模)如图,一次函数y=kx+b(k≠0)与y=x+2的图象相交于点M(m,4),则关于x的一元一次不等式kx﹣2<x﹣b的解集为( )
A.x>4 B.x<4 C.x>2 D.x<2
7.(2024 东海县一模)函数y=kx+b的图象如图所示,下列说法正确的是( )
A.当x=﹣2时,y=1
B.k<0
C.若y=kx+b的图象与坐标轴围成的三角形面积为2,则b=2
D.若点(﹣1,m)和点(1,n)在直线上,则m>n
8.(2024 拱墅区二模)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则( )
A.当x>2时,y1<y2 B.当x<0时,y1>3,y2<3
C.b﹣n=2(m﹣a) D.关于x,y的方程组的解为
9.(2024 榆阳区三模)在平面直角坐标系中,若直线l1:y=x+k与x轴交于点A(﹣3,0),与直线l2:y=kx﹣3(k≠0)交于点B,则交点B的坐标为( )
A.(0,﹣3) B.(﹣3,0) C.(3,6) D.(6,3)
10.(2024 内蒙古)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米.
(2)该同学在体育场锻炼了15分钟.
(3)该同学跑步的平均速度是步行平均速度的2倍.
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2024 湖北模拟)直线y=ax+b(a≠0)与x轴交于点(2024,0),与y轴交于点(0,﹣2025),则关于x的方程ax+b=0的解为x= .
12.(2024 凉州区二模)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 .
13.(2024 怀集县二模)已知一次函数y=﹣x+m与y=2x﹣1的图象如图所示,则关于x,y的方程组的解为 .
14.(2024 阳谷县一模)已知直线y=kx+b与直线y=2x+6平行,且经过点(0,3),那么该直线的表达式是 .
15.(2024 上海)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额1000万元,当投入90万元时销售量5000万元.则投入80万元时,销售额为 万元.
16.(2024 瓯海区模拟)如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx﹣3的解集是 .
三、解答题
17.(2024 玉环市二模)如图,直线y=k1x+b经过点A(﹣3,0),B(﹣1,2).
(1)求直线AB的表达式;
(2)若直线OB的解析式为:y=k2x,直接写出不等式k2x>k1x+b的解集.
18.(2024 山海关区一模)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=kx﹣5k(k<0),
(1)求点A的坐标;
(2)若直线l2与直线l1有交点C(1,1),求△BCO的面积;
(3)在(2)的条件下,y轴是否存在点P使得△PAO面积与△CAO面积相等,若存在,请直接写出P点的坐标;若不存在,请说明理由.
19.(2024 河北模拟)如图所示,直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点,直线y=kx+2﹣4k(k>0)与直线y=﹣x﹣2相交于C点.
(1)请说明y=kx+2﹣4k(k>0)经过点(4,2);
(2)k=1时,点D是直线y=kx+2﹣4k(k>0)上一点,若S△DOB=2S△DOA,求点D的坐标;
(3)若点C在第三象限,求k的取值范围.
20.(2024 眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
21.(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为 ;
(2)当≤x≤a时,求y与x之间的函数关系式;
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)
22.(2024 房山区二模)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点(4,1)和(0,﹣1).
(1)求这个一次函数的解析式;
(2)当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.
23.(2024 河北模拟)如图,在平面直角坐标系中,直线l1:y=kx+b经过点A(﹣2,6),且与x轴、y轴分别相交于点B、D,与直线l2:y=2x相交于点C,点C的横坐标为1.
(1)求直线l1的解析式;
(2)点P(a,0)是x轴上的一个动点,过点P与x轴垂直的直线MN与直线l1、l2分别相交于点E、F,且点E和点F关于x轴对称,求点P的坐标;
(3)若直线l3:y=mx+m与线段CD有交点(包括线段CD的两个端点),直接写出m的取值范围.
答案与解析
一、选择题
1.(2024 阎良区二模)如图,已知直线y=kx+b(k、b为常数,k≠0),则关于x的方程kx+b=1的解是x=( )
A.﹣4 B.﹣1 C.0 D.﹣2
【点拨】根据题意知,当y=1时,x=﹣4,据此求得关于x的方程kx+b=1的解.
【解析】解:∵点(﹣4,1)在直线y=kx+b(k,b是常数,k≠0)上,
∴当y=1时,x=﹣4.
∴关于x的方程kx+b=1的解x=﹣4.
故选:A.
【点睛】此题主要考查了一次函数与一元一次方程的关系,关键是正确利用已知条件“点(﹣4,1)在直线y=kx+b(k,b是常数,k≠0)上”解答.
2.(2023 南海区一模)某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )
A.y=20x B.y=40﹣2x C. D.y=x(40﹣2x)
【点拨】由木栏的总长,可得出2x+y=40,变形后,即可得出结论.
【解析】解:∵木栏总长为40m,
∴2x+y=40,
∴y=40﹣2x.
故选:B.
【点睛】本题考查了根据实际问题列一次函数关系式,根据各数量之间的关系,找出y与x满足的函数关系是解题的关键.
3.(2024 庄浪县二模)如图,一次函数y=kx+2(k为常数且k≠0)和y=3x+1的图象相交于点A,根据图象可知关于x的方程kx+2=3x+1的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
【点拨】由y=3x+1求得交点A的横坐标,即可求得关于x的方程kx+2=3x+1的解.
【解析】解:把y=4代入y=3x+1得,4=3x+1,
解得x=1,
∴点A的横坐标为1,
∴关于x的方程kx+2=3x+1的解是x=1,
故选:A.
【点睛】此题考查了一次函数图象上点的坐标特征,一次函数与一元一次方程的关系,求得交点坐标是解题的关键.
4.(2024 昭阳区模拟)如图,直线y=ax+b(a≠0)过点A(0,2),B(3,0),则不等式ax+b>0的解集是( )
A.x>3 B.x<3 C.x>2 D.x<2
【点拨】由题意知,不等式ax+b>0的解集为一次函数图象在x轴上方部分所对应的x的取值范围,结合图象作答即可.
【解析】解:由题意知,不等式ax+b>0的解集为一次函数图象在x轴上方部分所对应的x的取值范围,
由图象可知,不等式ax+b>0的解集为x<3,
故选:B.
【点睛】本题考查了一次函数与不等式.数形结合是解题的关键.
5.(2024 秦都区二模)如图是一次函数y1=kx﹣2k与y2=x+a的图象,则下列选项正确的是( )
A.k>0
B.a>0
C.当x<2时,一次函数 y1=kx﹣2k的值都为负数
D.方程kx﹣2k=x+a的解是x=3
【点拨】根据一次函数图象的性质逐项判断即可解答.
【解析】解:∵y1=kx﹣2k的图象呈下降趋势,
∴k<0,
故A项错误;
∵y2=x+a的图象与y轴的交点在y轴的负半轴,
∴a<0,
故B项错误;
∵一次函数解析式为:y1=kx﹣2k=k(x﹣2),
∴当x=2时,y1=0,
∴一次函数与x轴的交点坐标为(2,0),
∴当x>2时,一次函数 y1=kx﹣2k的值大于0,
当x<2时,一次函数 y1=kx﹣2k的值小于0,
当x=2时,一次函数 y1=kx﹣2k的值等于0,
故C项错误;
∵由一次函数 y1=kx﹣2k与 y2=x+a的图象的交点可知
当x=3时一次函数 y1=kx﹣2k与一次函数 y2=x+a的值相等,
故D项正确;
故选:D.
【点睛】本题考查了一次函数图象的性质,掌握一次函数图象的性质是解题的关键.
6.(2024 揭阳一模)如图,一次函数y=kx+b(k≠0)与y=x+2的图象相交于点M(m,4),则关于x的一元一次不等式kx﹣2<x﹣b的解集为( )
A.x>4 B.x<4 C.x>2 D.x<2
【点拨】先利用解析式y=x+2确定M点坐标,然后结合函数图象写出y=kx+b在y=x+2下方所对应的自变量的范围即可.
【解析】解:把M(m,4)代入y=x+2,得m+2=4,
解得m=2,
则M(2,4),
∵kx﹣2<x﹣b,
∴kx+b<x+2,
由图象得关于x的不等式kx+b<x+2的解集为x>2.
即关于x的一元一次不等式kx﹣2<x﹣b的解集为x>2.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
7.(2024 东海县一模)函数y=kx+b的图象如图所示,下列说法正确的是( )
A.当x=﹣2时,y=1
B.k<0
C.若y=kx+b的图象与坐标轴围成的三角形面积为2,则b=2
D.若点(﹣1,m)和点(1,n)在直线上,则m>n
【点拨】利用x=2时,y=0可对A选项进行判断;根据一次函数的性质可对B、D选项进行判断;由于直线与y轴的正半轴的交点坐标为(0,b),根据三角形面积公式得到×2×b=2,解方程求出b,从而可对C选项进行判断.
【解析】解:∵直线经过点(﹣2,0),
∴当x=﹣2时,y=0,所以A选项不符合题意;
∵一次函数图象经过第一、三象限,
∴k>0,所以B选项不符合题意;
∵一次函数y=kx+b与x轴的交点坐标为(﹣2,0),与y轴的正半轴的交点坐标为(0,b),
∴×2×b=2,
解得b=2,所以C选项符合题意;
若点(﹣1,m)和点(1,n)在直线y=kx+b上,
而y随x的增大而增大,
∴m<n,所以D选项不符合题意.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一次函数的性质.
8.(2024 拱墅区二模)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则( )
A.当x>2时,y1<y2 B.当x<0时,y1>3,y2<3
C.b﹣n=2(m﹣a) D.关于x,y的方程组的解为
【点拨】根据一次函数与方程、不等式的关系求解.
【解析】解:A、由图象得:当x>2时,y1>y2,故A不符合题意;
B、由图象得:当x<0时,y1<3,y2>3,故B不符合题意;
C、由图象得:当x﹣2时,y1=y2,即2a+b=2m+n,
∴b﹣n=2(m﹣a),故C是符合题意;
D、由图象得:关于x,y的方程组的解为,故D不符合题意.
故选:C.
【点睛】本题考查了一次函数与方程、不等式的关系,掌握数形结合思想是解题的关键.
9.(2024 榆阳区三模)在平面直角坐标系中,若直线l1:y=x+k与x轴交于点A(﹣3,0),与直线l2:y=kx﹣3(k≠0)交于点B,则交点B的坐标为( )
A.(0,﹣3) B.(﹣3,0) C.(3,6) D.(6,3)
【点拨】把点A(﹣3,0)代入y=x+k求得k的值,然后解析式联立成方程值,解方程值即可.
【解析】解:∵直线l1:y=x+k与x轴交于点A(﹣3,0),
∴﹣3+k=0,
∴k=3,
∴直线l1为y=x+3,直线l2为y=3x﹣3,
由,解得,
∴交点B的坐标为(3,6),
故选:C.
【点睛】本题是两条直线相交问题,考查了待定系数法求一次函数的解析式,两条直线交点的求法,求得两条直线的解析式是解题的关键.
10.(2024 内蒙古)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米.
(2)该同学在体育场锻炼了15分钟.
(3)该同学跑步的平均速度是步行平均速度的2倍.
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【点拨】根据函数的图象与坐标的关系求解.
【解析】解:(1)体育场离该同学家2.5千米,故(1)是正确的;
(2)该同学在体育场锻炼的时间为:30﹣15=15分钟,故(2)是正确的;
(3)该同学跑步的平均速度:步行平均速度=(65﹣30)÷15>2,故(3)是错误的;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,
则:a÷(103﹣88)=1.5×,
解得:a=3.75,
故(4)是正确的;
故选:C.
【点睛】本题考查了一次函数的应用,掌握数形结合思想是解题的关键.
二、填空题
11.(2024 湖北模拟)直线y=ax+b(a≠0)与x轴交于点(2024,0),与y轴交于点(0,﹣2025),则关于x的方程ax+b=0的解为x= 2024 .
【点拨】根据方程ax+b=0与一次函数y=ax+b的关系即可解决问题.
【解析】解:由题知,
方程ax+b=0的解可看成一次函数y=ax+b的图象与x轴交点的横坐标,
因为直线y=ax+b(a≠0)与x轴交于点(2024,0),
素以ax+b=0的解为x=2024.
故答案为:2024.
【点睛】本题考查一次函数与一元一次方程,熟知一次函数与一元一次方程之间的关系是解题的关键.
12.(2024 凉州区二模)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 x=1 .
【点拨】根据方程kx+b=2x的解,即为直线y=2x与y=kx+b的交点的横坐标的值解答即可.
【解析】解:∵直线y=2x与y=kx+b相交于点P(1,2),
∴方程kx+b=2x的解,即为直线y=2x与y=kx+b的交点的横坐标的值,
∴方程kx+b=2x的解为x=1,
故答案为:x=1.
【点睛】本题考查了一元一次方程与一次函数的关系,利用数形结合的思想解题是解答本题的关键.
13.(2024 怀集县二模)已知一次函数y=﹣x+m与y=2x﹣1的图象如图所示,则关于x,y的方程组的解为 .
【点拨】根据两函数交点即为两函数组成的方程组的解,从而求出答案.
【解析】解:∵y=﹣x+m与y=2x﹣1的图象交于(2,3),
∴关于x、y的方程组的解是.
故答案为:.
【点睛】本题考查了一次函数与二元一次方程组交点问题,可直接根据交点写出.
14.(2024 阳谷县一模)已知直线y=kx+b与直线y=2x+6平行,且经过点(0,3),那么该直线的表达式是 y=2x+3 .
【点拨】由两直线平行可得出k=2,根据直线上一点的坐标利用一次函数图象上点的坐标特征即可求出b值,此题得解.
【解析】解:∵直线y=kx+b与直线y=2x+6平行,
∴k=2,b≠6.
∵直线y=2x+b过点(0,3),
∴b=3.
故答案为:y=2x+3.
【点睛】本题考查了两条直线相交或平行问题以及一次函数图象上点的坐标特征,由两直线平行找出k=2、b≠6是解题的关键.
15.(2024 上海)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额1000万元,当投入90万元时销售量5000万元.则投入80万元时,销售额为 4500 万元.
【点拨】设y=kx+b,根据当投入10万元时销售额1000万元,当投入90万元时销售量5000万元,可得y=50x+500,令x=80得y=50×80+500=4500.
【解析】解:设y=kx+b,
∵当投入10万元时销售额1000万元,当投入90万元时销售量5000万元,
∴,
解得,
∴y=50x+500,
当x=80时,y=50×80+500=4500,
故答案为:4500.
【点睛】本题考查一次函数的应用,解题的关键是用待定系数法求出一次函数解析式.
16.(2024 瓯海区模拟)如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx﹣3的解集是 1<x<2 .
【点拨】由于一次函数y1同时经过A、P两点,可将它们的坐标分别代入y1的解析式中,即可求得k、b与m的关系,将其代入所求不等式组中,即可求得不等式的解集.
【解析】解:由于直线y1=kx+b过点A(0,3),P(1,m),
则有:,
解得.
∴直线y1=(m﹣3)x+3.
故所求不等式组可化为:mx>(m﹣3)x+3>mx﹣3,
解得:1<x<2.
故答案为:1<x<2.
【点睛】此题主要考查了一次函数与一元一次不等式,解决此题的关键是确定k、b与m的关系,从而通过解不等式组得到其解集.
三、解答题
17.(2024 玉环市二模)如图,直线y=k1x+b经过点A(﹣3,0),B(﹣1,2).
(1)求直线AB的表达式;
(2)若直线OB的解析式为:y=k2x,直接写出不等式k2x>k1x+b的解集.
【点拨】(1)根据待定系数法求解;
(2)根据不等式与函数的关系求解.
【解析】解:(1)由题意得:,
解得:,
所以:直线AB的表达式为y=x+3;
(2)由图象得:当x<﹣1时,k2x>k1x+b.
【点睛】本题考查了一次函数与一元一次不等式的关系,掌握待定系数法和不等式与函数的关系是解题的关键.
18.(2024 山海关区一模)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=kx﹣5k(k<0),
(1)求点A的坐标;
(2)若直线l2与直线l1有交点C(1,1),求△BCO的面积;
(3)在(2)的条件下,y轴是否存在点P使得△PAO面积与△CAO面积相等,若存在,请直接写出P点的坐标;若不存在,请说明理由.
【点拨】(1)令y=0,求得x=5,即可得到点A的坐标;
(2)利用待定系数法求得直线l2的解析式,得到点B的坐标,再利用三角形的面积公式求解即可;
(3)利用三角形的面积公式求得△CAO面积,再利用,求得OP=1,据此求解即可.
【解析】解:(1)令y=0,则kx﹣5k=0,解得x=5,
∴点A的坐标为(5,0);
(2)∵直线y=kx﹣5k(k<0)经过点C(1,1),
∴k﹣5k=1,解得,
∴直线l2的解析式为,
令x=0,则,
∴点B的坐标为;
∴△BCO的面积=;
(3)∵点A的坐标为(5,0),点C(1,1),
∴△CAO面积=,
∵△PAO面积与△CAO面积相等,
∴,
∴OP=1,
∴P点的坐标为(0,1)或(0,﹣1).
【点睛】本题考查了两条直线相交或平行问题、一次函数性质,熟练掌握待定系数法求函数的解析式是关键.
19.(2024 河北模拟)如图所示,直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点,直线y=kx+2﹣4k(k>0)与直线y=﹣x﹣2相交于C点.
(1)请说明y=kx+2﹣4k(k>0)经过点(4,2);
(2)k=1时,点D是直线y=kx+2﹣4k(k>0)上一点,若S△DOB=2S△DOA,求点D的坐标;
(3)若点C在第三象限,求k的取值范围.
【点拨】(1)把x=4代入函数关系求出y的值即可;
(2)先求出A,B的坐标,进而求出OA,OB的值,再设点D的坐标为(a,a﹣2),根据S△DOB=2S△DOA,列出方程求解即可;
(3)分别求出当直线y=kx+2﹣4k(k>0)经过点A,B时k的值即可.
【解析】解:(1)当x=4时,y=kx+2﹣4k=4k+2﹣4k=2,
∴点(4,2)在直线y=kx+2﹣4k(k>0)上.
(2)∵直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点
∴A(﹣2,0),B(0,﹣2),
∴OA=2=OB,
设D的坐标为(a,a﹣2),
∵S△DOB=2S△DOA,
∴a=2|a﹣2|,
∴a=4或
∴D(4,2)或.
(3)当直线y=kx+2﹣4k(k>0)经过点A时,0=﹣2k+2﹣4k,
解得:
当直线y=kx+2﹣4k(k>0)经过点B时,有﹣2=2﹣4k,
解得:k=1
∴若点C在第三象限,则.
【点睛】本题考查了一次函数与一元一次方程,是一次函数的综合题,利用数形结合进行分析是解题的关键.
20.(2024 眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
【点拨】(1)根据题意列出分式方程解答即可;
(2)设购进A款文创产品x件,则购进B款文创产品(100﹣x)件,总利润为W,根据题意列出不等式求出x取值范围,再列出W和x的函数关系式,根据函数性质确定x的取值,求出最大利润即可.
【解析】解:(1)A款文创产品每件的进价a元,则B文创产品每件的进价是(a﹣15)元,根据题意得:
,
解得:a=80,
经检验,a=80是原分式方程的解,
80﹣15=65.
答:A款文创产品每件的进价80元,则B文创产品每件的进价是65元.
(2)设购进A款文创产品x件,则购进B款文创产品(100﹣x)件,总利润为w,根据题意得:
80x+65(100﹣x)≤7400,
解得:x≤60,
∴w=(100﹣80)x+(80﹣65)(100﹣x)=5x+1500,
∵k=5>0,w随x的增大而增大,
∴当x=60时,利润最大,w最大=5×60+1500=1800.
答:购进A款文创产品60件,购进B款文创产品40件,才能使销售完后获得的利润最大,最大利润是1800元.
【点睛】本题考查了一次函数和分式方程的应用,熟练掌握一次函数性质是解答本题的关键.
21.(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为 ;
(2)当≤x≤a时,求y与x之间的函数关系式;
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)
【点拨】(1)根据可得以平均时速为100千米/时行驶a小时路程为20千米,据此可得a的值;
(2)利用待定系数法解答即可;
(3)求出先匀速行驶小时的速度即可判断.
【解析】解:(1)由题意得,100a=20,
解得a=,
故答案为:;
(2)设当≤x≤时,y与x之间的函数关系式为y=kx+b(k≠0),则:
,
解得,
∴y=90x+2(≤x≤);
(3)当x=时,y=90×+2=9.5,
∴先匀速行驶小时的速度为:=114(千米/时),
∵114<120,
∴这辆汽车减速前没有超速.
【点睛】本题考查了一次函数的应用,掌握待定系数法求函数关系式是解答本题的关键.
22.(2024 房山区二模)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点(4,1)和(0,﹣1).
(1)求这个一次函数的解析式;
(2)当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.
【点拨】(1)用待定系数法即可得到一次函数的解析式;
(2)根据点(﹣2,﹣2)结合图象即可求得.
【解析】解:(1)∵一次函数y=kx+b(k≠0)的图象经过(4,1),(0,﹣1),
∴,
∴,
∴一次函数解析式为;
(2)把x=﹣2代入,求得y=﹣2,
∴函数y=mx(m≠0)与一次函数的交点为(﹣2,﹣2),
把点(﹣2,﹣2)代入y=mx(m≠0),求得m=1,
当两直线平行时,,
如图,
∵当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数的值,
∴.
【点睛】本题主要考查了待定系数法求一次函数的解析式,一次函数图象与系数的关系,一次函数图象上点的坐标特征,熟练掌握其性质是解决此题的关键.
23.(2024 河北模拟)如图,在平面直角坐标系中,直线l1:y=kx+b经过点A(﹣2,6),且与x轴、y轴分别相交于点B、D,与直线l2:y=2x相交于点C,点C的横坐标为1.
(1)求直线l1的解析式;
(2)点P(a,0)是x轴上的一个动点,过点P与x轴垂直的直线MN与直线l1、l2分别相交于点E、F,且点E和点F关于x轴对称,求点P的坐标;
(3)若直线l3:y=mx+m与线段CD有交点(包括线段CD的两个端点),直接写出m的取值范围.
【点拨】(1)利用一次函数图象上点的坐标特征可求出点C的坐标,根据点A、C的坐标,利用待定系数法即可求出直线l1的解析式;
(2)将x=a分别代入直线y=﹣x+,y=2x,可得点E、F的坐标,根据点E与F关于x轴对称即可求解;
(3)求出点D(0,).将C、D的坐标分别代入y=mx+m求出m的值,即可得m的取值范围.
【解析】解:(1)当x=1时,y=2x=2,
∴点C的坐标为(1,2).
将A(﹣2,6)、C(1,2)代入y=kx+b,
∴,解得,
∴直线l1的解析式为y=﹣x+;
(2)∵点P(a,0),直线l2:y=2x,直线l1的解析式为y=﹣x+,
∴E(a,﹣a+)与F(a,2a),
∵E(a,﹣a+,)与F(a,2a)关于x轴对称,
∴﹣a++2a=0,
解得a=﹣5,
∴点P的坐标为(﹣5,0);
(3)∵一次函数y=﹣x+与y轴交于点D,
∴D(0,).
直线y=mx+m经过C(1,2)时,
m+m=2,解得m=1,
直线y=mx+m经过D(0,)时,m=,
∴直线y=mx+m与线段CD有交点时,m的取值范围为1≤m≤.
【点睛】本题是一次函数综合题,考查了待定系数法求一次函数的解析式,关于x轴对称的点的坐标特点,两直线相交问题,熟练掌握一次函数的相关性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题11 一次函数的应用与综合问题
一、选择题
1.(2024 阎良区二模)如图,已知直线y=kx+b(k、b为常数,k≠0),则关于x的方程kx+b=1的解是x=( )
A.﹣4 B.﹣1 C.0 D.﹣2
2.(2023 南海区一模)某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )
A.y=20x B.y=40﹣2x C. D.y=x(40﹣2x)
3.(2024 庄浪县二模)如图,一次函数y=kx+2(k为常数且k≠0)和y=3x+1的图象相交于点A,根据图象可知关于x的方程kx+2=3x+1的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
4.(2024 昭阳区模拟)如图,直线y=ax+b(a≠0)过点A(0,2),B(3,0),则不等式ax+b>0的解集是( )
A.x>3 B.x<3 C.x>2 D.x<2
5.(2024 秦都区二模)如图是一次函数y1=kx﹣2k与y2=x+a的图象,则下列选项正确的是( )
A.k>0
B.a>0
C.当x<2时,一次函数 y1=kx﹣2k的值都为负数
D.方程kx﹣2k=x+a的解是x=3
6.(2024 揭阳一模)如图,一次函数y=kx+b(k≠0)与y=x+2的图象相交于点M(m,4),则关于x的一元一次不等式kx﹣2<x﹣b的解集为( )
A.x>4 B.x<4 C.x>2 D.x<2
7.(2024 东海县一模)函数y=kx+b的图象如图所示,下列说法正确的是( )
A.当x=﹣2时,y=1
B.k<0
C.若y=kx+b的图象与坐标轴围成的三角形面积为2,则b=2
D.若点(﹣1,m)和点(1,n)在直线上,则m>n
8.(2024 拱墅区二模)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则( )
A.当x>2时,y1<y2 B.当x<0时,y1>3,y2<3
C.b﹣n=2(m﹣a) D.关于x,y的方程组的解为
9.(2024 榆阳区三模)在平面直角坐标系中,若直线l1:y=x+k与x轴交于点A(﹣3,0),与直线l2:y=kx﹣3(k≠0)交于点B,则交点B的坐标为( )
A.(0,﹣3) B.(﹣3,0) C.(3,6) D.(6,3)
10.(2024 内蒙古)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米.
(2)该同学在体育场锻炼了15分钟.
(3)该同学跑步的平均速度是步行平均速度的2倍.
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2024 湖北模拟)直线y=ax+b(a≠0)与x轴交于点(2024,0),与y轴交于点(0,﹣2025),则关于x的方程ax+b=0的解为x= .
12.(2024 凉州区二模)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 .
13.(2024 怀集县二模)已知一次函数y=﹣x+m与y=2x﹣1的图象如图所示,则关于x,y的方程组的解为 .
14.(2024 阳谷县一模)已知直线y=kx+b与直线y=2x+6平行,且经过点(0,3),那么该直线的表达式是 .
15.(2024 上海)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额1000万元,当投入90万元时销售量5000万元.则投入80万元时,销售额为 万元.
16.(2024 瓯海区模拟)如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx﹣3的解集是 .
三、解答题
17.(2024 玉环市二模)如图,直线y=k1x+b经过点A(﹣3,0),B(﹣1,2).
(1)求直线AB的表达式;
(2)若直线OB的解析式为:y=k2x,直接写出不等式k2x>k1x+b的解集.
18.(2024 山海关区一模)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=kx﹣5k(k<0),
(1)求点A的坐标;
(2)若直线l2与直线l1有交点C(1,1),求△BCO的面积;
(3)在(2)的条件下,y轴是否存在点P使得△PAO面积与△CAO面积相等,若存在,请直接写出P点的坐标;若不存在,请说明理由.
19.(2024 河北模拟)如图所示,直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点,直线y=kx+2﹣4k(k>0)与直线y=﹣x﹣2相交于C点.
(1)请说明y=kx+2﹣4k(k>0)经过点(4,2);
(2)k=1时,点D是直线y=kx+2﹣4k(k>0)上一点,若S△DOB=2S△DOA,求点D的坐标;
(3)若点C在第三象限,求k的取值范围.
20.(2024 眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
21.(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为 ;
(2)当≤x≤a时,求y与x之间的函数关系式;
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)
22.(2024 房山区二模)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点(4,1)和(0,﹣1).
(1)求这个一次函数的解析式;
(2)当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.
23.(2024 河北模拟)如图,在平面直角坐标系中,直线l1:y=kx+b经过点A(﹣2,6),且与x轴、y轴分别相交于点B、D,与直线l2:y=2x相交于点C,点C的横坐标为1.
(1)求直线l1的解析式;
(2)点P(a,0)是x轴上的一个动点,过点P与x轴垂直的直线MN与直线l1、l2分别相交于点E、F,且点E和点F关于x轴对称,求点P的坐标;
(3)若直线l3:y=mx+m与线段CD有交点(包括线段CD的两个端点),直接写出m的取值范围.
答案与解析
一、选择题
1.(2024 阎良区二模)如图,已知直线y=kx+b(k、b为常数,k≠0),则关于x的方程kx+b=1的解是x=( )
A.﹣4 B.﹣1 C.0 D.﹣2
【点拨】根据题意知,当y=1时,x=﹣4,据此求得关于x的方程kx+b=1的解.
【解析】解:∵点(﹣4,1)在直线y=kx+b(k,b是常数,k≠0)上,
∴当y=1时,x=﹣4.
∴关于x的方程kx+b=1的解x=﹣4.
故选:A.
【点睛】此题主要考查了一次函数与一元一次方程的关系,关键是正确利用已知条件“点(﹣4,1)在直线y=kx+b(k,b是常数,k≠0)上”解答.
2.(2023 南海区一模)某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )
A.y=20x B.y=40﹣2x C. D.y=x(40﹣2x)
【点拨】由木栏的总长,可得出2x+y=40,变形后,即可得出结论.
【解析】解:∵木栏总长为40m,
∴2x+y=40,
∴y=40﹣2x.
故选:B.
【点睛】本题考查了根据实际问题列一次函数关系式,根据各数量之间的关系,找出y与x满足的函数关系是解题的关键.
3.(2024 庄浪县二模)如图,一次函数y=kx+2(k为常数且k≠0)和y=3x+1的图象相交于点A,根据图象可知关于x的方程kx+2=3x+1的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
【点拨】由y=3x+1求得交点A的横坐标,即可求得关于x的方程kx+2=3x+1的解.
【解析】解:把y=4代入y=3x+1得,4=3x+1,
解得x=1,
∴点A的横坐标为1,
∴关于x的方程kx+2=3x+1的解是x=1,
故选:A.
【点睛】此题考查了一次函数图象上点的坐标特征,一次函数与一元一次方程的关系,求得交点坐标是解题的关键.
4.(2024 昭阳区模拟)如图,直线y=ax+b(a≠0)过点A(0,2),B(3,0),则不等式ax+b>0的解集是( )
A.x>3 B.x<3 C.x>2 D.x<2
【点拨】由题意知,不等式ax+b>0的解集为一次函数图象在x轴上方部分所对应的x的取值范围,结合图象作答即可.
【解析】解:由题意知,不等式ax+b>0的解集为一次函数图象在x轴上方部分所对应的x的取值范围,
由图象可知,不等式ax+b>0的解集为x<3,
故选:B.
【点睛】本题考查了一次函数与不等式.数形结合是解题的关键.
5.(2024 秦都区二模)如图是一次函数y1=kx﹣2k与y2=x+a的图象,则下列选项正确的是( )
A.k>0
B.a>0
C.当x<2时,一次函数 y1=kx﹣2k的值都为负数
D.方程kx﹣2k=x+a的解是x=3
【点拨】根据一次函数图象的性质逐项判断即可解答.
【解析】解:∵y1=kx﹣2k的图象呈下降趋势,
∴k<0,
故A项错误;
∵y2=x+a的图象与y轴的交点在y轴的负半轴,
∴a<0,
故B项错误;
∵一次函数解析式为:y1=kx﹣2k=k(x﹣2),
∴当x=2时,y1=0,
∴一次函数与x轴的交点坐标为(2,0),
∴当x>2时,一次函数 y1=kx﹣2k的值大于0,
当x<2时,一次函数 y1=kx﹣2k的值小于0,
当x=2时,一次函数 y1=kx﹣2k的值等于0,
故C项错误;
∵由一次函数 y1=kx﹣2k与 y2=x+a的图象的交点可知
当x=3时一次函数 y1=kx﹣2k与一次函数 y2=x+a的值相等,
故D项正确;
故选:D.
【点睛】本题考查了一次函数图象的性质,掌握一次函数图象的性质是解题的关键.
6.(2024 揭阳一模)如图,一次函数y=kx+b(k≠0)与y=x+2的图象相交于点M(m,4),则关于x的一元一次不等式kx﹣2<x﹣b的解集为( )
A.x>4 B.x<4 C.x>2 D.x<2
【点拨】先利用解析式y=x+2确定M点坐标,然后结合函数图象写出y=kx+b在y=x+2下方所对应的自变量的范围即可.
【解析】解:把M(m,4)代入y=x+2,得m+2=4,
解得m=2,
则M(2,4),
∵kx﹣2<x﹣b,
∴kx+b<x+2,
由图象得关于x的不等式kx+b<x+2的解集为x>2.
即关于x的一元一次不等式kx﹣2<x﹣b的解集为x>2.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
7.(2024 东海县一模)函数y=kx+b的图象如图所示,下列说法正确的是( )
A.当x=﹣2时,y=1
B.k<0
C.若y=kx+b的图象与坐标轴围成的三角形面积为2,则b=2
D.若点(﹣1,m)和点(1,n)在直线上,则m>n
【点拨】利用x=2时,y=0可对A选项进行判断;根据一次函数的性质可对B、D选项进行判断;由于直线与y轴的正半轴的交点坐标为(0,b),根据三角形面积公式得到×2×b=2,解方程求出b,从而可对C选项进行判断.
【解析】解:∵直线经过点(﹣2,0),
∴当x=﹣2时,y=0,所以A选项不符合题意;
∵一次函数图象经过第一、三象限,
∴k>0,所以B选项不符合题意;
∵一次函数y=kx+b与x轴的交点坐标为(﹣2,0),与y轴的正半轴的交点坐标为(0,b),
∴×2×b=2,
解得b=2,所以C选项符合题意;
若点(﹣1,m)和点(1,n)在直线y=kx+b上,
而y随x的增大而增大,
∴m<n,所以D选项不符合题意.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一次函数的性质.
8.(2024 拱墅区二模)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则( )
A.当x>2时,y1<y2 B.当x<0时,y1>3,y2<3
C.b﹣n=2(m﹣a) D.关于x,y的方程组的解为
【点拨】根据一次函数与方程、不等式的关系求解.
【解析】解:A、由图象得:当x>2时,y1>y2,故A不符合题意;
B、由图象得:当x<0时,y1<3,y2>3,故B不符合题意;
C、由图象得:当x﹣2时,y1=y2,即2a+b=2m+n,
∴b﹣n=2(m﹣a),故C是符合题意;
D、由图象得:关于x,y的方程组的解为,故D不符合题意.
故选:C.
【点睛】本题考查了一次函数与方程、不等式的关系,掌握数形结合思想是解题的关键.
9.(2024 榆阳区三模)在平面直角坐标系中,若直线l1:y=x+k与x轴交于点A(﹣3,0),与直线l2:y=kx﹣3(k≠0)交于点B,则交点B的坐标为( )
A.(0,﹣3) B.(﹣3,0) C.(3,6) D.(6,3)
【点拨】把点A(﹣3,0)代入y=x+k求得k的值,然后解析式联立成方程值,解方程值即可.
【解析】解:∵直线l1:y=x+k与x轴交于点A(﹣3,0),
∴﹣3+k=0,
∴k=3,
∴直线l1为y=x+3,直线l2为y=3x﹣3,
由,解得,
∴交点B的坐标为(3,6),
故选:C.
【点睛】本题是两条直线相交问题,考查了待定系数法求一次函数的解析式,两条直线交点的求法,求得两条直线的解析式是解题的关键.
10.(2024 内蒙古)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米.
(2)该同学在体育场锻炼了15分钟.
(3)该同学跑步的平均速度是步行平均速度的2倍.
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【点拨】根据函数的图象与坐标的关系求解.
【解析】解:(1)体育场离该同学家2.5千米,故(1)是正确的;
(2)该同学在体育场锻炼的时间为:30﹣15=15分钟,故(2)是正确的;
(3)该同学跑步的平均速度:步行平均速度=(65﹣30)÷15>2,故(3)是错误的;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,
则:a÷(103﹣88)=1.5×,
解得:a=3.75,
故(4)是正确的;
故选:C.
【点睛】本题考查了一次函数的应用,掌握数形结合思想是解题的关键.
二、填空题
11.(2024 湖北模拟)直线y=ax+b(a≠0)与x轴交于点(2024,0),与y轴交于点(0,﹣2025),则关于x的方程ax+b=0的解为x= 2024 .
【点拨】根据方程ax+b=0与一次函数y=ax+b的关系即可解决问题.
【解析】解:由题知,
方程ax+b=0的解可看成一次函数y=ax+b的图象与x轴交点的横坐标,
因为直线y=ax+b(a≠0)与x轴交于点(2024,0),
素以ax+b=0的解为x=2024.
故答案为:2024.
【点睛】本题考查一次函数与一元一次方程,熟知一次函数与一元一次方程之间的关系是解题的关键.
12.(2024 凉州区二模)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 x=1 .
【点拨】根据方程kx+b=2x的解,即为直线y=2x与y=kx+b的交点的横坐标的值解答即可.
【解析】解:∵直线y=2x与y=kx+b相交于点P(1,2),
∴方程kx+b=2x的解,即为直线y=2x与y=kx+b的交点的横坐标的值,
∴方程kx+b=2x的解为x=1,
故答案为:x=1.
【点睛】本题考查了一元一次方程与一次函数的关系,利用数形结合的思想解题是解答本题的关键.
13.(2024 怀集县二模)已知一次函数y=﹣x+m与y=2x﹣1的图象如图所示,则关于x,y的方程组的解为 .
【点拨】根据两函数交点即为两函数组成的方程组的解,从而求出答案.
【解析】解:∵y=﹣x+m与y=2x﹣1的图象交于(2,3),
∴关于x、y的方程组的解是.
故答案为:.
【点睛】本题考查了一次函数与二元一次方程组交点问题,可直接根据交点写出.
14.(2024 阳谷县一模)已知直线y=kx+b与直线y=2x+6平行,且经过点(0,3),那么该直线的表达式是 y=2x+3 .
【点拨】由两直线平行可得出k=2,根据直线上一点的坐标利用一次函数图象上点的坐标特征即可求出b值,此题得解.
【解析】解:∵直线y=kx+b与直线y=2x+6平行,
∴k=2,b≠6.
∵直线y=2x+b过点(0,3),
∴b=3.
故答案为:y=2x+3.
【点睛】本题考查了两条直线相交或平行问题以及一次函数图象上点的坐标特征,由两直线平行找出k=2、b≠6是解题的关键.
15.(2024 上海)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额1000万元,当投入90万元时销售量5000万元.则投入80万元时,销售额为 4500 万元.
【点拨】设y=kx+b,根据当投入10万元时销售额1000万元,当投入90万元时销售量5000万元,可得y=50x+500,令x=80得y=50×80+500=4500.
【解析】解:设y=kx+b,
∵当投入10万元时销售额1000万元,当投入90万元时销售量5000万元,
∴,
解得,
∴y=50x+500,
当x=80时,y=50×80+500=4500,
故答案为:4500.
【点睛】本题考查一次函数的应用,解题的关键是用待定系数法求出一次函数解析式.
16.(2024 瓯海区模拟)如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx﹣3的解集是 1<x<2 .
【点拨】由于一次函数y1同时经过A、P两点,可将它们的坐标分别代入y1的解析式中,即可求得k、b与m的关系,将其代入所求不等式组中,即可求得不等式的解集.
【解析】解:由于直线y1=kx+b过点A(0,3),P(1,m),
则有:,
解得.
∴直线y1=(m﹣3)x+3.
故所求不等式组可化为:mx>(m﹣3)x+3>mx﹣3,
解得:1<x<2.
故答案为:1<x<2.
【点睛】此题主要考查了一次函数与一元一次不等式,解决此题的关键是确定k、b与m的关系,从而通过解不等式组得到其解集.
三、解答题
17.(2024 玉环市二模)如图,直线y=k1x+b经过点A(﹣3,0),B(﹣1,2).
(1)求直线AB的表达式;
(2)若直线OB的解析式为:y=k2x,直接写出不等式k2x>k1x+b的解集.
【点拨】(1)根据待定系数法求解;
(2)根据不等式与函数的关系求解.
【解析】解:(1)由题意得:,
解得:,
所以:直线AB的表达式为y=x+3;
(2)由图象得:当x<﹣1时,k2x>k1x+b.
【点睛】本题考查了一次函数与一元一次不等式的关系,掌握待定系数法和不等式与函数的关系是解题的关键.
18.(2024 山海关区一模)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=kx﹣5k(k<0),
(1)求点A的坐标;
(2)若直线l2与直线l1有交点C(1,1),求△BCO的面积;
(3)在(2)的条件下,y轴是否存在点P使得△PAO面积与△CAO面积相等,若存在,请直接写出P点的坐标;若不存在,请说明理由.
【点拨】(1)令y=0,求得x=5,即可得到点A的坐标;
(2)利用待定系数法求得直线l2的解析式,得到点B的坐标,再利用三角形的面积公式求解即可;
(3)利用三角形的面积公式求得△CAO面积,再利用,求得OP=1,据此求解即可.
【解析】解:(1)令y=0,则kx﹣5k=0,解得x=5,
∴点A的坐标为(5,0);
(2)∵直线y=kx﹣5k(k<0)经过点C(1,1),
∴k﹣5k=1,解得,
∴直线l2的解析式为,
令x=0,则,
∴点B的坐标为;
∴△BCO的面积=;
(3)∵点A的坐标为(5,0),点C(1,1),
∴△CAO面积=,
∵△PAO面积与△CAO面积相等,
∴,
∴OP=1,
∴P点的坐标为(0,1)或(0,﹣1).
【点睛】本题考查了两条直线相交或平行问题、一次函数性质,熟练掌握待定系数法求函数的解析式是关键.
19.(2024 河北模拟)如图所示,直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点,直线y=kx+2﹣4k(k>0)与直线y=﹣x﹣2相交于C点.
(1)请说明y=kx+2﹣4k(k>0)经过点(4,2);
(2)k=1时,点D是直线y=kx+2﹣4k(k>0)上一点,若S△DOB=2S△DOA,求点D的坐标;
(3)若点C在第三象限,求k的取值范围.
【点拨】(1)把x=4代入函数关系求出y的值即可;
(2)先求出A,B的坐标,进而求出OA,OB的值,再设点D的坐标为(a,a﹣2),根据S△DOB=2S△DOA,列出方程求解即可;
(3)分别求出当直线y=kx+2﹣4k(k>0)经过点A,B时k的值即可.
【解析】解:(1)当x=4时,y=kx+2﹣4k=4k+2﹣4k=2,
∴点(4,2)在直线y=kx+2﹣4k(k>0)上.
(2)∵直线y=﹣x﹣2与x轴相交于A点,与y轴相交于B点
∴A(﹣2,0),B(0,﹣2),
∴OA=2=OB,
设D的坐标为(a,a﹣2),
∵S△DOB=2S△DOA,
∴a=2|a﹣2|,
∴a=4或
∴D(4,2)或.
(3)当直线y=kx+2﹣4k(k>0)经过点A时,0=﹣2k+2﹣4k,
解得:
当直线y=kx+2﹣4k(k>0)经过点B时,有﹣2=2﹣4k,
解得:k=1
∴若点C在第三象限,则.
【点睛】本题考查了一次函数与一元一次方程,是一次函数的综合题,利用数形结合进行分析是解题的关键.
20.(2024 眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
【点拨】(1)根据题意列出分式方程解答即可;
(2)设购进A款文创产品x件,则购进B款文创产品(100﹣x)件,总利润为W,根据题意列出不等式求出x取值范围,再列出W和x的函数关系式,根据函数性质确定x的取值,求出最大利润即可.
【解析】解:(1)A款文创产品每件的进价a元,则B文创产品每件的进价是(a﹣15)元,根据题意得:
,
解得:a=80,
经检验,a=80是原分式方程的解,
80﹣15=65.
答:A款文创产品每件的进价80元,则B文创产品每件的进价是65元.
(2)设购进A款文创产品x件,则购进B款文创产品(100﹣x)件,总利润为w,根据题意得:
80x+65(100﹣x)≤7400,
解得:x≤60,
∴w=(100﹣80)x+(80﹣65)(100﹣x)=5x+1500,
∵k=5>0,w随x的增大而增大,
∴当x=60时,利润最大,w最大=5×60+1500=1800.
答:购进A款文创产品60件,购进B款文创产品40件,才能使销售完后获得的利润最大,最大利润是1800元.
【点睛】本题考查了一次函数和分式方程的应用,熟练掌握一次函数性质是解答本题的关键.
21.(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为 ;
(2)当≤x≤a时,求y与x之间的函数关系式;
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)
【点拨】(1)根据可得以平均时速为100千米/时行驶a小时路程为20千米,据此可得a的值;
(2)利用待定系数法解答即可;
(3)求出先匀速行驶小时的速度即可判断.
【解析】解:(1)由题意得,100a=20,
解得a=,
故答案为:;
(2)设当≤x≤时,y与x之间的函数关系式为y=kx+b(k≠0),则:
,
解得,
∴y=90x+2(≤x≤);
(3)当x=时,y=90×+2=9.5,
∴先匀速行驶小时的速度为:=114(千米/时),
∵114<120,
∴这辆汽车减速前没有超速.
【点睛】本题考查了一次函数的应用,掌握待定系数法求函数关系式是解答本题的关键.
22.(2024 房山区二模)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点(4,1)和(0,﹣1).
(1)求这个一次函数的解析式;
(2)当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.
【点拨】(1)用待定系数法即可得到一次函数的解析式;
(2)根据点(﹣2,﹣2)结合图象即可求得.
【解析】解:(1)∵一次函数y=kx+b(k≠0)的图象经过(4,1),(0,﹣1),
∴,
∴,
∴一次函数解析式为;
(2)把x=﹣2代入,求得y=﹣2,
∴函数y=mx(m≠0)与一次函数的交点为(﹣2,﹣2),
把点(﹣2,﹣2)代入y=mx(m≠0),求得m=1,
当两直线平行时,,
如图,
∵当x>﹣2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数的值,
∴.
【点睛】本题主要考查了待定系数法求一次函数的解析式,一次函数图象与系数的关系,一次函数图象上点的坐标特征,熟练掌握其性质是解决此题的关键.
23.(2024 河北模拟)如图,在平面直角坐标系中,直线l1:y=kx+b经过点A(﹣2,6),且与x轴、y轴分别相交于点B、D,与直线l2:y=2x相交于点C,点C的横坐标为1.
(1)求直线l1的解析式;
(2)点P(a,0)是x轴上的一个动点,过点P与x轴垂直的直线MN与直线l1、l2分别相交于点E、F,且点E和点F关于x轴对称,求点P的坐标;
(3)若直线l3:y=mx+m与线段CD有交点(包括线段CD的两个端点),直接写出m的取值范围.
【点拨】(1)利用一次函数图象上点的坐标特征可求出点C的坐标,根据点A、C的坐标,利用待定系数法即可求出直线l1的解析式;
(2)将x=a分别代入直线y=﹣x+,y=2x,可得点E、F的坐标,根据点E与F关于x轴对称即可求解;
(3)求出点D(0,).将C、D的坐标分别代入y=mx+m求出m的值,即可得m的取值范围.
【解析】解:(1)当x=1时,y=2x=2,
∴点C的坐标为(1,2).
将A(﹣2,6)、C(1,2)代入y=kx+b,
∴,解得,
∴直线l1的解析式为y=﹣x+;
(2)∵点P(a,0),直线l2:y=2x,直线l1的解析式为y=﹣x+,
∴E(a,﹣a+)与F(a,2a),
∵E(a,﹣a+,)与F(a,2a)关于x轴对称,
∴﹣a++2a=0,
解得a=﹣5,
∴点P的坐标为(﹣5,0);
(3)∵一次函数y=﹣x+与y轴交于点D,
∴D(0,).
直线y=mx+m经过C(1,2)时,
m+m=2,解得m=1,
直线y=mx+m经过D(0,)时,m=,
∴直线y=mx+m与线段CD有交点时,m的取值范围为1≤m≤.
【点睛】本题是一次函数综合题,考查了待定系数法求一次函数的解析式,关于x轴对称的点的坐标特点,两直线相交问题,熟练掌握一次函数的相关性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
