江苏省南京市雨花台中学2024-2025苏科版七年级下数学第5周阶段性训练试卷(含详解)
文档属性
| 名称 | 江苏省南京市雨花台中学2024-2025苏科版七年级下数学第5周阶段性训练试卷(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 532.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 00:00:00 | ||
图片预览



文档简介
江苏省南京市雨花台中学2024-2025苏科版七下数学第5周阶段性训练
一.选择题(共3小题)
1.设a=﹣0.32,b=﹣32,c=(﹣)﹣2,d=(﹣)0,则a,b,c,d的大小关系是( )
A.a<b<c<d B.b<a<c<d C.b<a<d<c D.a<b<d<c
2.下列命题中,真命题是( )
A.如果a2=b2,那么a=b.
B.三角形的三条高线交于一点
C.两条直线被第三条直线所截,同位角相等
D.在同一平面内,两边分别平行的两角相等或互补
3.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是( )
A.③④ B.①②④ C.①②③ D.①②③④
二.填空题(共10小题)
4.若24+24=2a,35+35+35=3b,则a﹣b的值为 .
5.5811的个位数字为 .
6.已知5a=4,5b=6,5c=9,则a,b,c之间满足的等量关系是 .
7.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 cm.
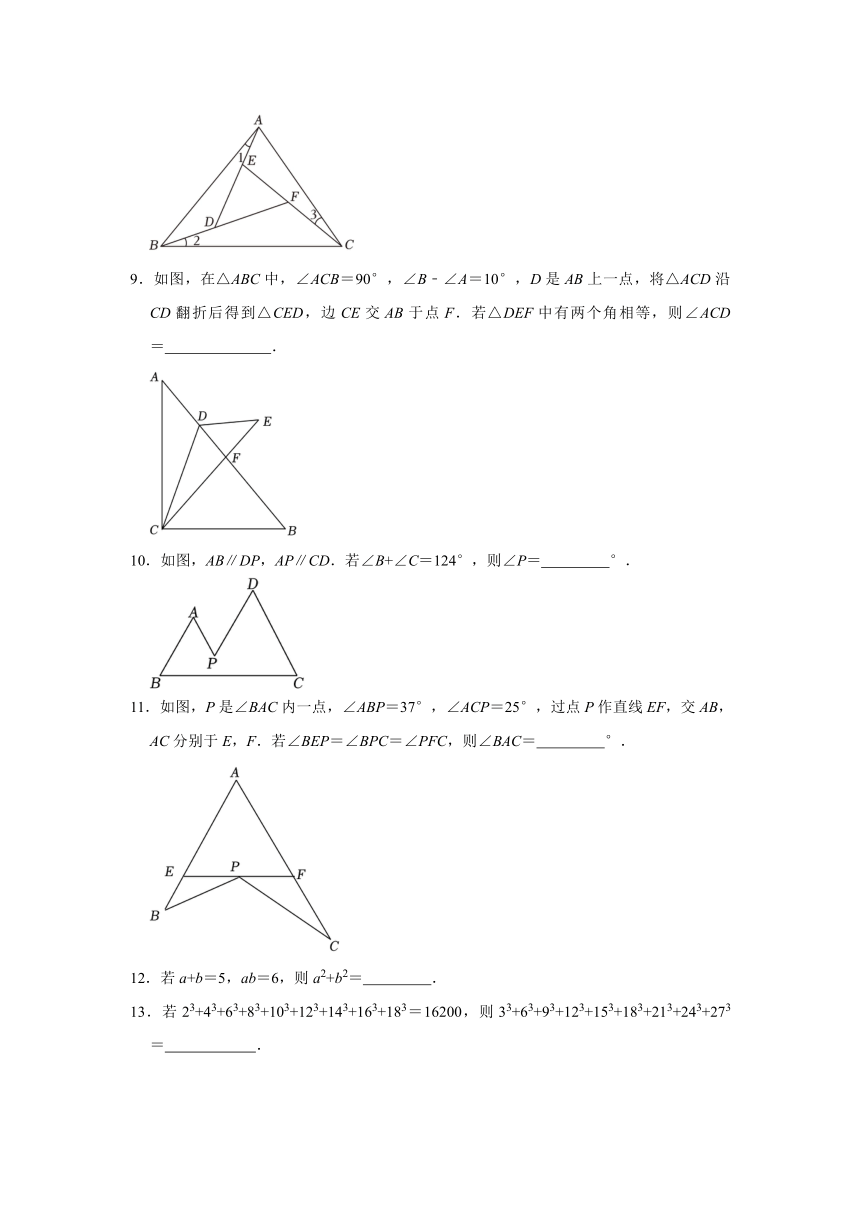
8.如图,在△ABC中,∠1=∠2=∠3.若∠ABC=45°,∠DFE=50°,则∠BAC= °.
9.如图,在△ABC中,∠ACB=90°,∠B﹣∠A=10°,D是AB上一点,将△ACD沿CD翻折后得到△CED,边CE交AB于点F.若△DEF中有两个角相等,则∠ACD= .
10.如图,AB∥DP,AP∥CD.若∠B+∠C=124°,则∠P= °.
11.如图,P是∠BAC内一点,∠ABP=37°,∠ACP=25°,过点P作直线EF,交AB,AC分别于E,F.若∠BEP=∠BPC=∠PFC,则∠BAC= °.
12.若a+b=5,ab=6,则a2+b2= .
13.若23+43+63+83+103+123+143+163+183=16200,则33+63+93+123+153+183+213+243+273= .
三.解答题(共3小题)
14.【概念学习】我们知道:如果一条射线把一个角分成两个相等的角,这条射线叫做这个角的角平分线.我们规定:如果两条射线把一个角分成三个相等的角,这两条射线都叫做这个角的角三分线.如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD、BE叫∠ABC的角三分线.其中BD是“邻AB角三分线”,BE是“邻BC角三分线”.
【概念理解】(1)如图2,在△ABC中,∠A=55°,∠B=65°,若∠C的角三分线CD交AB于点D,则∠ADC= .
【概念应用】(2)如图3,在△ABC中,BP、CP分别是∠ABC邻AB角三分线和∠ACB邻AC角三分线,若∠BPC=100°,求∠A的度数;
【延伸推广】(3)在△ABC中,∠ABD是△ABC的外角,∠C的角三分线与∠ABD的角三分线交于点P,若∠A=m°,∠C=n°,请直接写出分类情况和相应的∠BPC的度数.
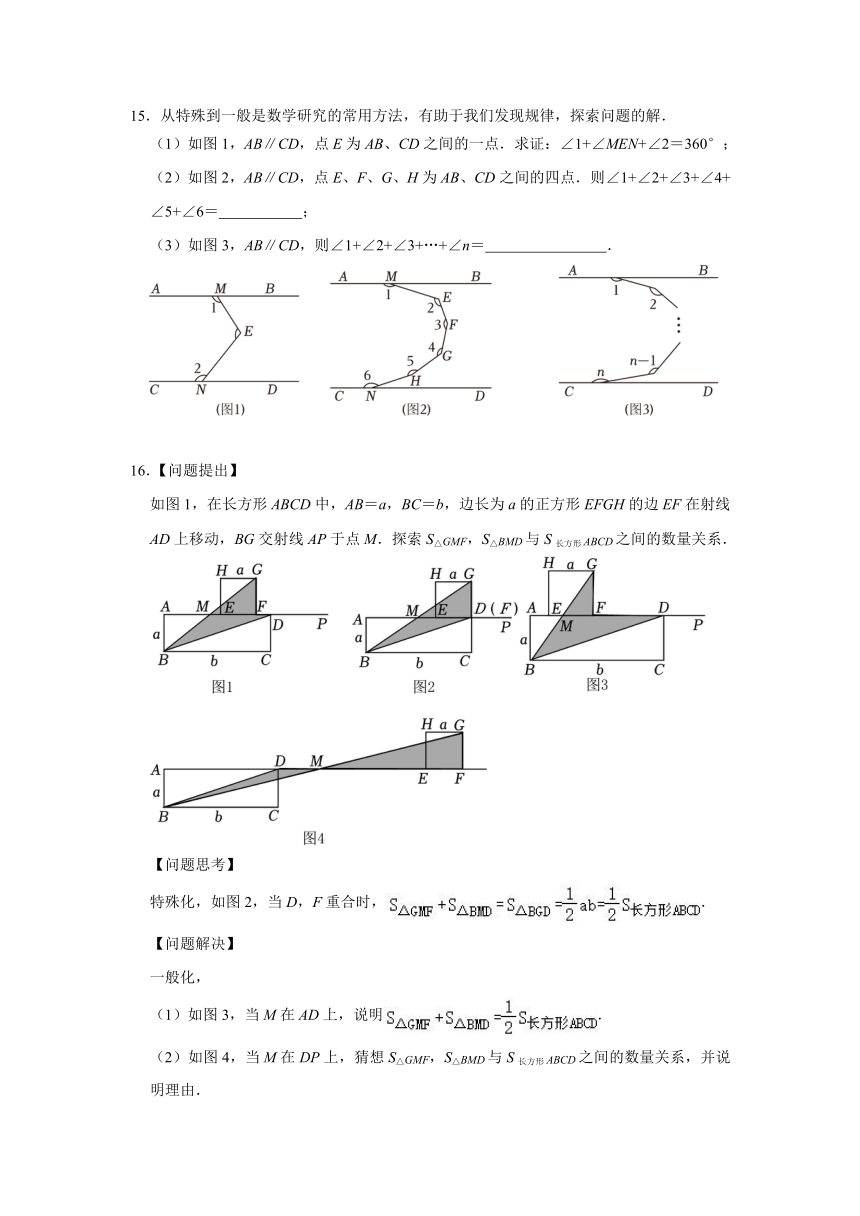
15.从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解.
(1)如图1,AB∥CD,点E为AB、CD之间的一点.求证:∠1+∠MEN+∠2=360°;
(2)如图2,AB∥CD,点E、F、G、H为AB、CD之间的四点.则∠1+∠2+∠3+∠4+∠5+∠6= ;
(3)如图3,AB∥CD,则∠1+∠2+∠3+…+∠n= .
16.【问题提出】
如图1,在长方形ABCD中,AB=a,BC=b,边长为a的正方形EFGH的边EF在射线AD上移动,BG交射线AP于点M.探索S△GMF,S△BMD与S长方形ABCD之间的数量关系.
【问题思考】
特殊化,如图2,当D,F重合时,.
【问题解决】
一般化,
(1)如图3,当M在AD上,说明.
(2)如图4,当M在DP上,猜想S△GMF,S△BMD与S长方形ABCD之间的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:∵a=﹣0.09,b=﹣9,c=32=9,d=1,
又∵﹣9<﹣0.09<1<9,
∴b<a<d<c.
故选:C.
2.【解答】解:A、如果a2=b2,那么a=±b,故本选项说法是假命题,不符合题意;
B、三角形的三条高所在的直线交于一点,故本选项说法是假命题,不符合题意;
C、两条平行线被第三条直线所截,同位角相等,故本选项说法是假命题,不符合题意;
D、在同一平面内,两边分别平行的两角相等或互补,是真命题,符合题意;
故选:D.
3.【解答】解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故正确;
④无法证明CA平分∠BCG,故错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正确;
②∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴,
∴∠DFE=360°﹣135°﹣90°=135°,
∴,
∴∠CGE=2∠DFB,
∴,故正确.
∴正确的为:①②③,
故选:C.
二.填空题(共10小题)
4.【解答】解:∵24+24=2a,35+35+35=3b,
∴2a=2×24=25,3b=3×35=36.
∴a=5,b=6.
∴a﹣b=5﹣6=﹣1.
故答案为:﹣1.
5.【解答】解:∵8的一次方尾数是8,
8的二次方尾数是4,
8的3次方尾数是2,
8的四次方尾数是6,
8的5次方尾数是8,
……
∴尾数四个一循环,次序8、4、2、6.
∵11÷4=2……3,
∴5811的个位数字为:2.
故答案为:2.
6.【解答】解:∵5a=4,5b=6,5c=9,
∴4×9=62,
∴5a 5c=(5b)2,
∴5a+c=52b,
∴a+c=2b,
故答案为:a+c=2b.
7.【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
8.【解答】解:∵∠EDF是△ABD的一个外角,
∴∠EDF=∠1+∠ABD,
∵∠1=∠2,
∴∠EDF=∠2+∠ABD=∠ABC,
即∠ABC=∠EDF;
∵∠DEF是△ACE的一个外角,
∴∠DEF=∠3+∠CAE,
∵∠1=∠3,
∴∠DEF=∠1+∠CAE=∠BAC,
得∠EDF=∠ABC=45°,
∵∠DFE=50°,
∴∠DEF=180°﹣∠EDF﹣∠DFE=85°,
即∠BAC=85°.
故答案为:85.
9.【解答】解:在△ABC中,∠ACB=90°,
∴∠B+∠A=90°,
∵∠B﹣∠A=10°,
∴∠A=40°,∠B=50°,
设∠ACD=x°,则∠CDF=(40+x)°,∠ADC=180°﹣40°﹣x°=(140﹣x)°,
由折叠可知:∠ADC=∠CDE,∠E=∠A=40°,
当∠DFE=∠E=40°时,
∵∠FDE+∠DFE+∠E=180°,
∴∠FDE=180°﹣40°﹣40°=100°,
∴140﹣x=100+40+x,
解得x=0(不存在);
当∠FDE=∠E=40°时,
∴140﹣x=40+40+x,
解得x=30,
即∠ACD=30°;
当∠DFE=∠FDE时,
∵∠FDE+∠DFE+∠E=180°,
∴∠FDE==70°,
∴140﹣x=70+40+x,
解得x=15,
即∠ACD=15°,
综上,∠ACD=15°或30°,
故答案为:15°或30°.
10.【解答】解:延长AP交BC于点E,如图,
∵AB∥DP,AP∥CD,
∴∠A=∠APD,∠C=∠AEB,
∵∠B+∠C=124°,
∴∠B+∠AEB=124°,
∴∠A=180°﹣(∠B+∠AEB)=56°,
∴∠APD=56°.
故答案为:56.
11.【解答】解:如图,连接BC,
由题意知,∠BAC+∠ABP+∠PBC+∠PCB+∠ACP=180°,
∴∠PBC+∠PCB=118°﹣∠BAC,
∵∠BEP=∠BPC=∠PFC,
∴,,
∵∠BPC+∠PBC+∠PCB=180°,
∴,
解得∠BAC=56°,
故答案为:56.
12.【解答】解:a2+b2=(a+b)2﹣2ab=13.
13.【解答】解:∵23+43+63+83+103+123+143+163+183
=23×(13+23+33+……+93)
=
=16200,
∴33+63+93+123+153+183+213+243+273
=33×(13+23+33+……93)
=
=54675.
故答案为:54675.
三.解答题(共3小题)
14.【解答】解:(1)∵∠A=55°,∠B=65°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣55°﹣65°=60°,
①当CD是“邻AC三分线”时,∠BCD=∠ACB=×60°=40°,
∴∠ADC=∠BCD+∠B=40°+65°=105°;
②当CD是“邻BC三分线”时,∠BCD=∠ACB=×60°=20°,
∠ADC=∠BCD+∠B=20°+65°=85°;
综上所述,∠ADC为85°或105°,
故答案为:85°或105°;
(2)∵BP、CP分别是∠ABC邻AB角三分线和∠ACB邻AC角三分线,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∵∠BPC=100°,
∴∠PBC+∠PCB=180°﹣∠BPC=180°﹣100°=80°,
∵∠PBC+∠PCB=(∠ABC+∠ACB),
∴(∠ABC+∠ACB)=80°,
∴∠ABC+∠ACB=120°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣120°=60°;
(3)分为四种情况:
①如图1,当BP和CP分别是“邻AB三分线”、“邻AC三分线”时,
∠PCB=∠ACB=n°,
由题意得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=m°;
②如图2,当BP和CP分别是“邻AB三分线”、“邻BC三分线”时,
∠PCB=∠ACB=n°,
由题意可知:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=;
③如图3,当BP和CP分别是“邻BD三分线”、“邻AC三分线”时,
当m°>n°时,如图3,
∠PCB=∠ACB=n°,
由外角可得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=;
当m°<n°时,如图4,
∠FCB=∠ACB=n°,
由题意得:∠DBE=∠PBC=∠ABD=(m°+n°),
∴∠BPC=∠FCB﹣∠PBC=n°﹣(m°+n°)=;
④如图5,当BP和CP分别是“邻BD三分线”、“邻BC三分线”时,
∠PCB=∠ACB=n°,
由题意得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=m°;
综合上述,∠BPC的度数是m°或或或或m°.
15.【解答】(1)证明:过点E作EF∥CD,
∵AB∥CD,
∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°,
∴∠1+∠2+∠MEN=360;
(2)解:过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,
∵CD∥AB,
∴EQ∥FW∥GR∥HY∥AB∥CD,
∴∠1+∠MEQ=180°,∠QEF+∠EFW=180°,∠WFG+∠FGR=180°,∠RGH+∠GHY=180°,∠YHN+∠6=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°.
故答案为:900°;
(3)解:同(2)理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n﹣1).
故答案为:180°(n﹣1).
16.【解答】(1)证明:在△BMA和△GMF中,
,
∴△BMA≌△GMF(AAS),
∴S△BMA=S△GMF,
∴,
∴;
(2)解:.理由如下:
同(1)可知△BMA≌△GMF(AAS),则S△BMA=S△GMF,
∴,
∴.
一.选择题(共3小题)
1.设a=﹣0.32,b=﹣32,c=(﹣)﹣2,d=(﹣)0,则a,b,c,d的大小关系是( )
A.a<b<c<d B.b<a<c<d C.b<a<d<c D.a<b<d<c
2.下列命题中,真命题是( )
A.如果a2=b2,那么a=b.
B.三角形的三条高线交于一点
C.两条直线被第三条直线所截,同位角相等
D.在同一平面内,两边分别平行的两角相等或互补
3.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是( )
A.③④ B.①②④ C.①②③ D.①②③④
二.填空题(共10小题)
4.若24+24=2a,35+35+35=3b,则a﹣b的值为 .
5.5811的个位数字为 .
6.已知5a=4,5b=6,5c=9,则a,b,c之间满足的等量关系是 .
7.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 cm.
8.如图,在△ABC中,∠1=∠2=∠3.若∠ABC=45°,∠DFE=50°,则∠BAC= °.
9.如图,在△ABC中,∠ACB=90°,∠B﹣∠A=10°,D是AB上一点,将△ACD沿CD翻折后得到△CED,边CE交AB于点F.若△DEF中有两个角相等,则∠ACD= .
10.如图,AB∥DP,AP∥CD.若∠B+∠C=124°,则∠P= °.
11.如图,P是∠BAC内一点,∠ABP=37°,∠ACP=25°,过点P作直线EF,交AB,AC分别于E,F.若∠BEP=∠BPC=∠PFC,则∠BAC= °.
12.若a+b=5,ab=6,则a2+b2= .
13.若23+43+63+83+103+123+143+163+183=16200,则33+63+93+123+153+183+213+243+273= .
三.解答题(共3小题)
14.【概念学习】我们知道:如果一条射线把一个角分成两个相等的角,这条射线叫做这个角的角平分线.我们规定:如果两条射线把一个角分成三个相等的角,这两条射线都叫做这个角的角三分线.如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD、BE叫∠ABC的角三分线.其中BD是“邻AB角三分线”,BE是“邻BC角三分线”.
【概念理解】(1)如图2,在△ABC中,∠A=55°,∠B=65°,若∠C的角三分线CD交AB于点D,则∠ADC= .
【概念应用】(2)如图3,在△ABC中,BP、CP分别是∠ABC邻AB角三分线和∠ACB邻AC角三分线,若∠BPC=100°,求∠A的度数;
【延伸推广】(3)在△ABC中,∠ABD是△ABC的外角,∠C的角三分线与∠ABD的角三分线交于点P,若∠A=m°,∠C=n°,请直接写出分类情况和相应的∠BPC的度数.
15.从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解.
(1)如图1,AB∥CD,点E为AB、CD之间的一点.求证:∠1+∠MEN+∠2=360°;
(2)如图2,AB∥CD,点E、F、G、H为AB、CD之间的四点.则∠1+∠2+∠3+∠4+∠5+∠6= ;
(3)如图3,AB∥CD,则∠1+∠2+∠3+…+∠n= .
16.【问题提出】
如图1,在长方形ABCD中,AB=a,BC=b,边长为a的正方形EFGH的边EF在射线AD上移动,BG交射线AP于点M.探索S△GMF,S△BMD与S长方形ABCD之间的数量关系.
【问题思考】
特殊化,如图2,当D,F重合时,.
【问题解决】
一般化,
(1)如图3,当M在AD上,说明.
(2)如图4,当M在DP上,猜想S△GMF,S△BMD与S长方形ABCD之间的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:∵a=﹣0.09,b=﹣9,c=32=9,d=1,
又∵﹣9<﹣0.09<1<9,
∴b<a<d<c.
故选:C.
2.【解答】解:A、如果a2=b2,那么a=±b,故本选项说法是假命题,不符合题意;
B、三角形的三条高所在的直线交于一点,故本选项说法是假命题,不符合题意;
C、两条平行线被第三条直线所截,同位角相等,故本选项说法是假命题,不符合题意;
D、在同一平面内,两边分别平行的两角相等或互补,是真命题,符合题意;
故选:D.
3.【解答】解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故正确;
④无法证明CA平分∠BCG,故错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正确;
②∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴,
∴∠DFE=360°﹣135°﹣90°=135°,
∴,
∴∠CGE=2∠DFB,
∴,故正确.
∴正确的为:①②③,
故选:C.
二.填空题(共10小题)
4.【解答】解:∵24+24=2a,35+35+35=3b,
∴2a=2×24=25,3b=3×35=36.
∴a=5,b=6.
∴a﹣b=5﹣6=﹣1.
故答案为:﹣1.
5.【解答】解:∵8的一次方尾数是8,
8的二次方尾数是4,
8的3次方尾数是2,
8的四次方尾数是6,
8的5次方尾数是8,
……
∴尾数四个一循环,次序8、4、2、6.
∵11÷4=2……3,
∴5811的个位数字为:2.
故答案为:2.
6.【解答】解:∵5a=4,5b=6,5c=9,
∴4×9=62,
∴5a 5c=(5b)2,
∴5a+c=52b,
∴a+c=2b,
故答案为:a+c=2b.
7.【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
8.【解答】解:∵∠EDF是△ABD的一个外角,
∴∠EDF=∠1+∠ABD,
∵∠1=∠2,
∴∠EDF=∠2+∠ABD=∠ABC,
即∠ABC=∠EDF;
∵∠DEF是△ACE的一个外角,
∴∠DEF=∠3+∠CAE,
∵∠1=∠3,
∴∠DEF=∠1+∠CAE=∠BAC,
得∠EDF=∠ABC=45°,
∵∠DFE=50°,
∴∠DEF=180°﹣∠EDF﹣∠DFE=85°,
即∠BAC=85°.
故答案为:85.
9.【解答】解:在△ABC中,∠ACB=90°,
∴∠B+∠A=90°,
∵∠B﹣∠A=10°,
∴∠A=40°,∠B=50°,
设∠ACD=x°,则∠CDF=(40+x)°,∠ADC=180°﹣40°﹣x°=(140﹣x)°,
由折叠可知:∠ADC=∠CDE,∠E=∠A=40°,
当∠DFE=∠E=40°时,
∵∠FDE+∠DFE+∠E=180°,
∴∠FDE=180°﹣40°﹣40°=100°,
∴140﹣x=100+40+x,
解得x=0(不存在);
当∠FDE=∠E=40°时,
∴140﹣x=40+40+x,
解得x=30,
即∠ACD=30°;
当∠DFE=∠FDE时,
∵∠FDE+∠DFE+∠E=180°,
∴∠FDE==70°,
∴140﹣x=70+40+x,
解得x=15,
即∠ACD=15°,
综上,∠ACD=15°或30°,
故答案为:15°或30°.
10.【解答】解:延长AP交BC于点E,如图,
∵AB∥DP,AP∥CD,
∴∠A=∠APD,∠C=∠AEB,
∵∠B+∠C=124°,
∴∠B+∠AEB=124°,
∴∠A=180°﹣(∠B+∠AEB)=56°,
∴∠APD=56°.
故答案为:56.
11.【解答】解:如图,连接BC,
由题意知,∠BAC+∠ABP+∠PBC+∠PCB+∠ACP=180°,
∴∠PBC+∠PCB=118°﹣∠BAC,
∵∠BEP=∠BPC=∠PFC,
∴,,
∵∠BPC+∠PBC+∠PCB=180°,
∴,
解得∠BAC=56°,
故答案为:56.
12.【解答】解:a2+b2=(a+b)2﹣2ab=13.
13.【解答】解:∵23+43+63+83+103+123+143+163+183
=23×(13+23+33+……+93)
=
=16200,
∴33+63+93+123+153+183+213+243+273
=33×(13+23+33+……93)
=
=54675.
故答案为:54675.
三.解答题(共3小题)
14.【解答】解:(1)∵∠A=55°,∠B=65°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣55°﹣65°=60°,
①当CD是“邻AC三分线”时,∠BCD=∠ACB=×60°=40°,
∴∠ADC=∠BCD+∠B=40°+65°=105°;
②当CD是“邻BC三分线”时,∠BCD=∠ACB=×60°=20°,
∠ADC=∠BCD+∠B=20°+65°=85°;
综上所述,∠ADC为85°或105°,
故答案为:85°或105°;
(2)∵BP、CP分别是∠ABC邻AB角三分线和∠ACB邻AC角三分线,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∵∠BPC=100°,
∴∠PBC+∠PCB=180°﹣∠BPC=180°﹣100°=80°,
∵∠PBC+∠PCB=(∠ABC+∠ACB),
∴(∠ABC+∠ACB)=80°,
∴∠ABC+∠ACB=120°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣120°=60°;
(3)分为四种情况:
①如图1,当BP和CP分别是“邻AB三分线”、“邻AC三分线”时,
∠PCB=∠ACB=n°,
由题意得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=m°;
②如图2,当BP和CP分别是“邻AB三分线”、“邻BC三分线”时,
∠PCB=∠ACB=n°,
由题意可知:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=;
③如图3,当BP和CP分别是“邻BD三分线”、“邻AC三分线”时,
当m°>n°时,如图3,
∠PCB=∠ACB=n°,
由外角可得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=;
当m°<n°时,如图4,
∠FCB=∠ACB=n°,
由题意得:∠DBE=∠PBC=∠ABD=(m°+n°),
∴∠BPC=∠FCB﹣∠PBC=n°﹣(m°+n°)=;
④如图5,当BP和CP分别是“邻BD三分线”、“邻BC三分线”时,
∠PCB=∠ACB=n°,
由题意得:∠PBD=∠ABD=(m°+n°),
∴∠BPC=∠PBD﹣∠PCB=(m°+n°)﹣n°=m°;
综合上述,∠BPC的度数是m°或或或或m°.
15.【解答】(1)证明:过点E作EF∥CD,
∵AB∥CD,
∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°,
∴∠1+∠2+∠MEN=360;
(2)解:过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,
∵CD∥AB,
∴EQ∥FW∥GR∥HY∥AB∥CD,
∴∠1+∠MEQ=180°,∠QEF+∠EFW=180°,∠WFG+∠FGR=180°,∠RGH+∠GHY=180°,∠YHN+∠6=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°.
故答案为:900°;
(3)解:同(2)理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n﹣1).
故答案为:180°(n﹣1).
16.【解答】(1)证明:在△BMA和△GMF中,
,
∴△BMA≌△GMF(AAS),
∴S△BMA=S△GMF,
∴,
∴;
(2)解:.理由如下:
同(1)可知△BMA≌△GMF(AAS),则S△BMA=S△GMF,
∴,
∴.
同课章节目录
