北师大版小学数学六年级下册第一单元圆柱和圆锥综合素养测评A卷(含答案)
文档属性
| 名称 | 北师大版小学数学六年级下册第一单元圆柱和圆锥综合素养测评A卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 870.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-16 20:03:46 | ||
图片预览



文档简介
第一单元综合素养测评 A卷
“四基”与“四能”
时间:90分钟 满分:100分+10分
一、填空。(每空1分,共18分)
1.550 dm3=( ) m3 38000 cm2=( ) dm2
0.09 L=( ) mL 4600 mL=( ) cm3=( ) dm3
2.把一张长15.7 dm、宽8 dm 的长方形硬纸板卷成一个圆柱形纸
筒(接口处忽略不计) ,这个圆柱形纸筒的底面周长是( )
dm,高是( ) dm,侧面积是( ) dm2 。
3.用玉米笼装玉米,不仅能减少晾晒玉米的占地面积,还能起到很好的通风作用。李伯伯用铁丝网围成了一个圆柱形的玉米笼,如图,这个玉米笼大约能圈( ) m3 的玉米棒。(忽略玉米棒间的空隙)
4. 曹冲称象时,利用转化的思想,把大象的质量转化成石头的质量。我们在推导圆柱体积公式时,也利用了转化的思想,把圆柱转化成近似的长方体。如图,若转化成的长方体的长是6.28 dm,高是3 dm ,则原来这个圆柱的底面半径是( ) dm,体积是( ) dm3 。
5.如图,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件, 每个圆锥形零件的体积是( ) cm3 。
6.一个圆锥的体积是21 cm3,底面积是7 cm2 ,它的高是( ) cm 。
7.一个圆锥形橡皮泥,底面积是36 cm2,高是12 cm 。若把它捏
成同样高的圆柱,则圆柱的底面积是( ) cm2 ;若把它捏成底面积与圆锥相等的圆柱,则圆柱的高是( ) cm 。
8.如图,一个圆柱形蛋糕盒的底面半径是10 cm,用8 m 长的彩带正好可以捆扎5个这样的蛋糕盒(打结处均长20 cm) , 这个蛋糕盒的高是( ) cm 。
9.把一块石头浸没在一个底面周长是62.8 cm 的圆柱形容器里,容器里的水面高度上升了1.2 cm (水未溢出) ,这块石头的体积是( ) cm3 。
10.如图,如果将一段圆柱形木料截成两个小圆柱,那么它的表面积将增加6.28 cm2 ;如果将它沿底面直径垂直底面截成体积相等的两部分,那么它的表面积将增加80 cm2 。原来这段圆柱形木料的体积是( ) cm3 。
二、选择。(每题2分,共12分)
1.一个圆柱形喷水池,底面直径是10 m,深0.75 m 。求这个喷水
池的占地面积,下面列式正确的是( ) 。
A.3.14×(10÷2) 2 B.10×3.14×0.75
C.3.14×(10÷2) 2+3.14×10×0.75 D.3.14×102
2.如图,下面两个三角形分别绕轴旋转一周后所形成的图形甲、
乙的体积相比较,( ) 。
A. _甲= _乙 B. _甲< _乙
C. _甲> _乙 D.无法比较
3.如果正方体、圆柱、圆锥的底面积相等,高也相等,那么下列
说法正确的是( ) 。
A.圆锥的体积是正方体的 B.圆柱的体积是圆锥的
C.圆柱的体积比正方体的体积小 D.圆柱和正方体的表面积相等
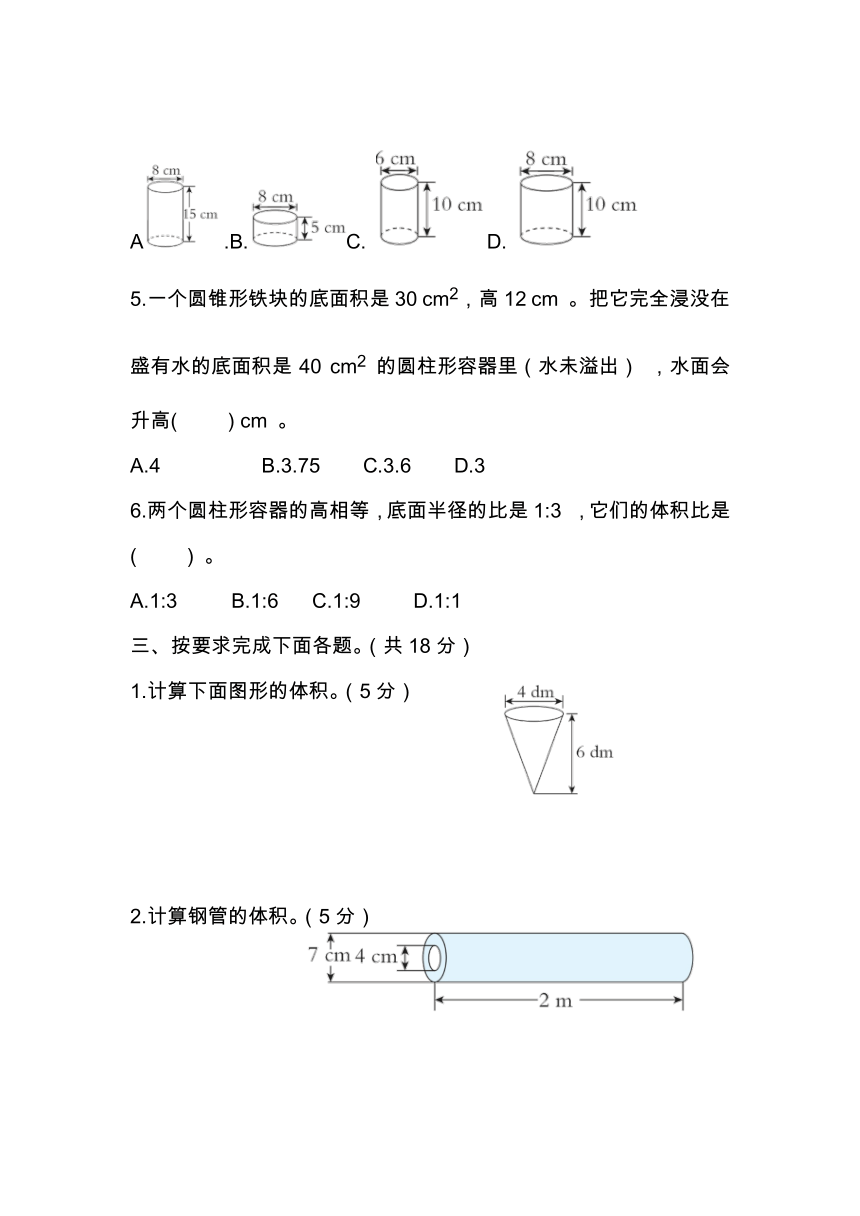
4.如图,一个圆锥形容器内装满了水,将这些水全部倒入圆柱形容器( ) 中正好装满。(容器厚度忽略不计)
A.B.C. D.
5.一个圆锥形铁块的底面积是30 cm2,高12 cm 。把它完全浸没在盛有水的底面积是40 cm2 的圆柱形容器里(水未溢出) ,水面会升高( ) cm 。
A.4 B.3.75 C.3.6 D.3
6.两个圆柱形容器的高相等,底面半径的比是1:3 ,它们的体积比是( ) 。
A.1:3 B.1:6 C.1:9 D.1:1
三、按要求完成下面各题。(共18分)
1.计算下面图形的体积。(5分)
2.计算钢管的体积。(5分)
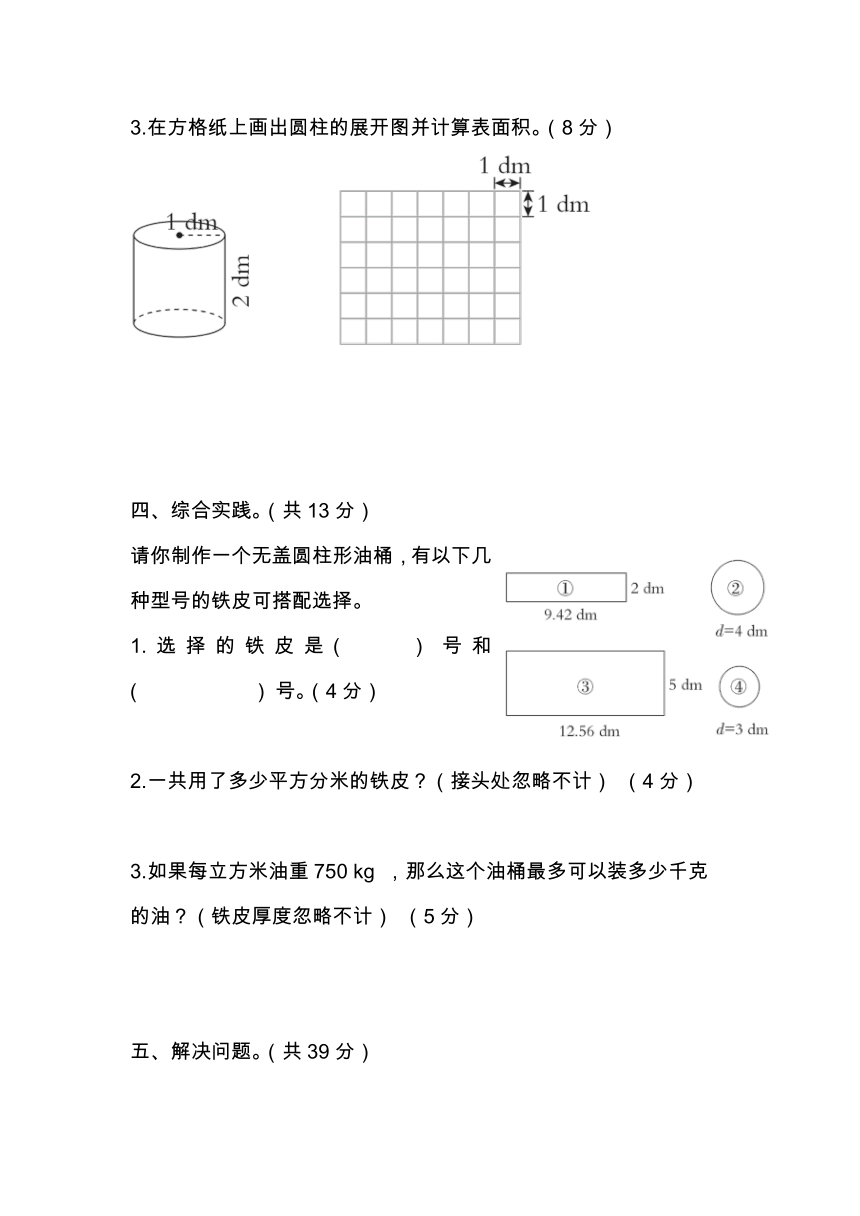
3.在方格纸上画出圆柱的展开图并计算表面积。(8分)
四、综合实践。(共13分)
请你制作一个无盖圆柱形油桶,有以下几种型号的铁皮可搭配选择。
1.选择的铁皮是( ) 号和( ) 号。(4分)
2.一共用了多少平方分米的铁皮?(接头处忽略不计) (4分)
3.如果每立方米油重750 kg ,那么这个油桶最多可以装多少千克
的油?(铁皮厚度忽略不计) (5分)
五、解决问题。(共39分)
1.同同想用硬纸板做一个底面半径是6 cm,高15 cm 的圆柱形笔筒。
如果接缝处不计,那么做这个笔筒至少需要多少平方厘米的硬纸
板?(5分)
2. 一堆煤呈圆锥形,底面直径为6 m,高1.5 m,每立方米煤重1.4t 。当李叔叔用一辆质量为3 t 的卡车一次性运走这堆煤时,能安全通过图中的桥吗?试通过计算说明。(6分)
3.一根高8 m的圆柱形木料,把它的高截短3 m 后,表面积减少了
18.84 m^2 。这根圆柱形木料的体积减少了多少立方米?(5分)
4.我们在探究圆柱的体积公式时,是将一个圆柱转化为一个近似的长方体得到的。现在将转化得到的长方体翻转一下摆放,如图。
1)观察上图,我们发现翻转后长方体的底面积等于圆柱的( ) ,长方体的高等于圆柱的( ) ,因此圆柱的体积还可以这样计算:__________________________________。(4分)
(2)用你的发现解决下面的问题。(4分)
有一个圆柱,侧面积是80 dm^2,底面半径是5 dm ,它的体积是
多少?
5.为了测量一个瓶子的容积,蓝蓝所在的学习小组进行了实验(如图) ,并记录下相关数据。
①整个瓶子的高度是23 cm ;
②瓶子圆柱形部分的内直径是6 cm ;
③把瓶子正放时,水的高度是5 cm ;
④把瓶子倒放时,无水部分是圆柱形,高是15 cm 。
(1)要求这个瓶子的容积,上面记录中有用的信息是( ) 。(填序号) (3分)
(2)请根据选出的信息,求出这个瓶子的容积。(5分)
6.如图,饮料瓶中装满饮料,现在要将饮料倒入圆锥形的玻璃杯中。已知玻璃杯杯口的直径是饮料瓶底面直径的一半,饮料瓶中的饮料一
共能倒满多少杯?(7分)
挑战题:甲、乙两个圆柱形容器,底面积之比是2:3 ,甲容器中的水深是6 cm,乙容器中的水深是8 cm 。现在往两个容器中加入同样多
的水,使两个容器中的水深相等,这时容器中的水深是多少厘米?
参考答案
一、1.
2. 15.7 8 125.6(或8 15.7 125.6)
3. 5.652
4.2 37.68
5.120
6.9
7.12 4
8.15
9. 376.8
10. 62.8
二、1.A 2.C 3.A 4.B 5.D 6.C
三、1.
2.
3.
四、1. ① ④(或② ③)
2. 选①④。
9.42×2+3.14×(3÷2) 2=25.905(dm2)
答:一共用了25.905 dm2 的铁皮。
选②③。
12.56×5+3.14×(4÷2) 2=75.36(dm2)
答:一共用了75.36 dm2 的铁皮。
3.
五、1. 3.14×62+3.14×6×2×15=678.24(cm2)
答:做这个笔筒至少需要678.24 cm2 的硬纸板。
2. 3.14×(6÷2)2×1.5÷3×1.4=19.782(t)
19.782+3=22.782(t)
22.782>20
答:不能安全通过图中的桥。
3. 18.84÷3÷3.14÷2=1(m)
3.14×1^2×3=9.42(m3)
答:这根圆柱形木料的体积减少了9.42 m3 。
4.(1)侧面积的一半 底面半径 圆柱的体积=圆柱侧面积的一半×底面半径
(2)80÷2×5=200(dm3)
答:它的体积是200 dm3 。
5.(1)②③④
(2)3.14×(6÷2) 2×(5+15)=565.2(cm3)
565.2 cm3=565.2 mL
答:这个瓶子的容积是565.2 mL 。
6. 饮料瓶的底面积∶玻璃杯的底面积=22:1=4:1
饮料瓶的体积∶玻璃杯的体积=4×(8+12):1×8×=30:1
答:饮料瓶中的饮料一共能倒满30杯。
挑战题:解:设这时容器中的水深是 cm 。
( 6)×2=( 8)×3
=12
答:这时容器中的水深是12 cm 。
“四基”与“四能”
时间:90分钟 满分:100分+10分
一、填空。(每空1分,共18分)
1.550 dm3=( ) m3 38000 cm2=( ) dm2
0.09 L=( ) mL 4600 mL=( ) cm3=( ) dm3
2.把一张长15.7 dm、宽8 dm 的长方形硬纸板卷成一个圆柱形纸
筒(接口处忽略不计) ,这个圆柱形纸筒的底面周长是( )
dm,高是( ) dm,侧面积是( ) dm2 。
3.用玉米笼装玉米,不仅能减少晾晒玉米的占地面积,还能起到很好的通风作用。李伯伯用铁丝网围成了一个圆柱形的玉米笼,如图,这个玉米笼大约能圈( ) m3 的玉米棒。(忽略玉米棒间的空隙)
4. 曹冲称象时,利用转化的思想,把大象的质量转化成石头的质量。我们在推导圆柱体积公式时,也利用了转化的思想,把圆柱转化成近似的长方体。如图,若转化成的长方体的长是6.28 dm,高是3 dm ,则原来这个圆柱的底面半径是( ) dm,体积是( ) dm3 。
5.如图,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件, 每个圆锥形零件的体积是( ) cm3 。
6.一个圆锥的体积是21 cm3,底面积是7 cm2 ,它的高是( ) cm 。
7.一个圆锥形橡皮泥,底面积是36 cm2,高是12 cm 。若把它捏
成同样高的圆柱,则圆柱的底面积是( ) cm2 ;若把它捏成底面积与圆锥相等的圆柱,则圆柱的高是( ) cm 。
8.如图,一个圆柱形蛋糕盒的底面半径是10 cm,用8 m 长的彩带正好可以捆扎5个这样的蛋糕盒(打结处均长20 cm) , 这个蛋糕盒的高是( ) cm 。
9.把一块石头浸没在一个底面周长是62.8 cm 的圆柱形容器里,容器里的水面高度上升了1.2 cm (水未溢出) ,这块石头的体积是( ) cm3 。
10.如图,如果将一段圆柱形木料截成两个小圆柱,那么它的表面积将增加6.28 cm2 ;如果将它沿底面直径垂直底面截成体积相等的两部分,那么它的表面积将增加80 cm2 。原来这段圆柱形木料的体积是( ) cm3 。
二、选择。(每题2分,共12分)
1.一个圆柱形喷水池,底面直径是10 m,深0.75 m 。求这个喷水
池的占地面积,下面列式正确的是( ) 。
A.3.14×(10÷2) 2 B.10×3.14×0.75
C.3.14×(10÷2) 2+3.14×10×0.75 D.3.14×102
2.如图,下面两个三角形分别绕轴旋转一周后所形成的图形甲、
乙的体积相比较,( ) 。
A. _甲= _乙 B. _甲< _乙
C. _甲> _乙 D.无法比较
3.如果正方体、圆柱、圆锥的底面积相等,高也相等,那么下列
说法正确的是( ) 。
A.圆锥的体积是正方体的 B.圆柱的体积是圆锥的
C.圆柱的体积比正方体的体积小 D.圆柱和正方体的表面积相等
4.如图,一个圆锥形容器内装满了水,将这些水全部倒入圆柱形容器( ) 中正好装满。(容器厚度忽略不计)
A.B.C. D.
5.一个圆锥形铁块的底面积是30 cm2,高12 cm 。把它完全浸没在盛有水的底面积是40 cm2 的圆柱形容器里(水未溢出) ,水面会升高( ) cm 。
A.4 B.3.75 C.3.6 D.3
6.两个圆柱形容器的高相等,底面半径的比是1:3 ,它们的体积比是( ) 。
A.1:3 B.1:6 C.1:9 D.1:1
三、按要求完成下面各题。(共18分)
1.计算下面图形的体积。(5分)
2.计算钢管的体积。(5分)
3.在方格纸上画出圆柱的展开图并计算表面积。(8分)
四、综合实践。(共13分)
请你制作一个无盖圆柱形油桶,有以下几种型号的铁皮可搭配选择。
1.选择的铁皮是( ) 号和( ) 号。(4分)
2.一共用了多少平方分米的铁皮?(接头处忽略不计) (4分)
3.如果每立方米油重750 kg ,那么这个油桶最多可以装多少千克
的油?(铁皮厚度忽略不计) (5分)
五、解决问题。(共39分)
1.同同想用硬纸板做一个底面半径是6 cm,高15 cm 的圆柱形笔筒。
如果接缝处不计,那么做这个笔筒至少需要多少平方厘米的硬纸
板?(5分)
2. 一堆煤呈圆锥形,底面直径为6 m,高1.5 m,每立方米煤重1.4t 。当李叔叔用一辆质量为3 t 的卡车一次性运走这堆煤时,能安全通过图中的桥吗?试通过计算说明。(6分)
3.一根高8 m的圆柱形木料,把它的高截短3 m 后,表面积减少了
18.84 m^2 。这根圆柱形木料的体积减少了多少立方米?(5分)
4.我们在探究圆柱的体积公式时,是将一个圆柱转化为一个近似的长方体得到的。现在将转化得到的长方体翻转一下摆放,如图。
1)观察上图,我们发现翻转后长方体的底面积等于圆柱的( ) ,长方体的高等于圆柱的( ) ,因此圆柱的体积还可以这样计算:__________________________________。(4分)
(2)用你的发现解决下面的问题。(4分)
有一个圆柱,侧面积是80 dm^2,底面半径是5 dm ,它的体积是
多少?
5.为了测量一个瓶子的容积,蓝蓝所在的学习小组进行了实验(如图) ,并记录下相关数据。
①整个瓶子的高度是23 cm ;
②瓶子圆柱形部分的内直径是6 cm ;
③把瓶子正放时,水的高度是5 cm ;
④把瓶子倒放时,无水部分是圆柱形,高是15 cm 。
(1)要求这个瓶子的容积,上面记录中有用的信息是( ) 。(填序号) (3分)
(2)请根据选出的信息,求出这个瓶子的容积。(5分)
6.如图,饮料瓶中装满饮料,现在要将饮料倒入圆锥形的玻璃杯中。已知玻璃杯杯口的直径是饮料瓶底面直径的一半,饮料瓶中的饮料一
共能倒满多少杯?(7分)
挑战题:甲、乙两个圆柱形容器,底面积之比是2:3 ,甲容器中的水深是6 cm,乙容器中的水深是8 cm 。现在往两个容器中加入同样多
的水,使两个容器中的水深相等,这时容器中的水深是多少厘米?
参考答案
一、1.
2. 15.7 8 125.6(或8 15.7 125.6)
3. 5.652
4.2 37.68
5.120
6.9
7.12 4
8.15
9. 376.8
10. 62.8
二、1.A 2.C 3.A 4.B 5.D 6.C
三、1.
2.
3.
四、1. ① ④(或② ③)
2. 选①④。
9.42×2+3.14×(3÷2) 2=25.905(dm2)
答:一共用了25.905 dm2 的铁皮。
选②③。
12.56×5+3.14×(4÷2) 2=75.36(dm2)
答:一共用了75.36 dm2 的铁皮。
3.
五、1. 3.14×62+3.14×6×2×15=678.24(cm2)
答:做这个笔筒至少需要678.24 cm2 的硬纸板。
2. 3.14×(6÷2)2×1.5÷3×1.4=19.782(t)
19.782+3=22.782(t)
22.782>20
答:不能安全通过图中的桥。
3. 18.84÷3÷3.14÷2=1(m)
3.14×1^2×3=9.42(m3)
答:这根圆柱形木料的体积减少了9.42 m3 。
4.(1)侧面积的一半 底面半径 圆柱的体积=圆柱侧面积的一半×底面半径
(2)80÷2×5=200(dm3)
答:它的体积是200 dm3 。
5.(1)②③④
(2)3.14×(6÷2) 2×(5+15)=565.2(cm3)
565.2 cm3=565.2 mL
答:这个瓶子的容积是565.2 mL 。
6. 饮料瓶的底面积∶玻璃杯的底面积=22:1=4:1
饮料瓶的体积∶玻璃杯的体积=4×(8+12):1×8×=30:1
答:饮料瓶中的饮料一共能倒满30杯。
挑战题:解:设这时容器中的水深是 cm 。
( 6)×2=( 8)×3
=12
答:这时容器中的水深是12 cm 。
