第8章 三角形 能力培优测试卷(含答案) 2024-2025学年华东师大版七年级数学下册
文档属性
| 名称 | 第8章 三角形 能力培优测试卷(含答案) 2024-2025学年华东师大版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 167.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 00:00:00 | ||
图片预览

文档简介
第8章 三角形
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.关于三角形的三个内角,下列说法错误的是 ( )
A.必有一内角不小于60° B.最多有两个锐角
C.最少有两个锐角 D.必有一内角不大于60°
2.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E,HE是△AEC的中线,那么以AD为高的三角形有 ( )
A.2个 B.3个 C.5个 D.6个
3.若正多边形的一个外角是60°,则这个正多边形的边数是 ( )
A.4 B.5 C.6 D.7
4.若一个三角形的三个内角的度数比为2∶3∶4,则这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
5.如图,在△ABC中,∠C=90°,AD平分∠BAC,∠CDA=70°,则∠B的度数为( )
A.60° B.50° C.40° D.30°
6.用13根同样长的火柴棒在桌面上摆一个三角形(不许折断,且全部用完),能摆出不同形状的三角形的个数是 ( )
A.6 B.5 C.4 D.3
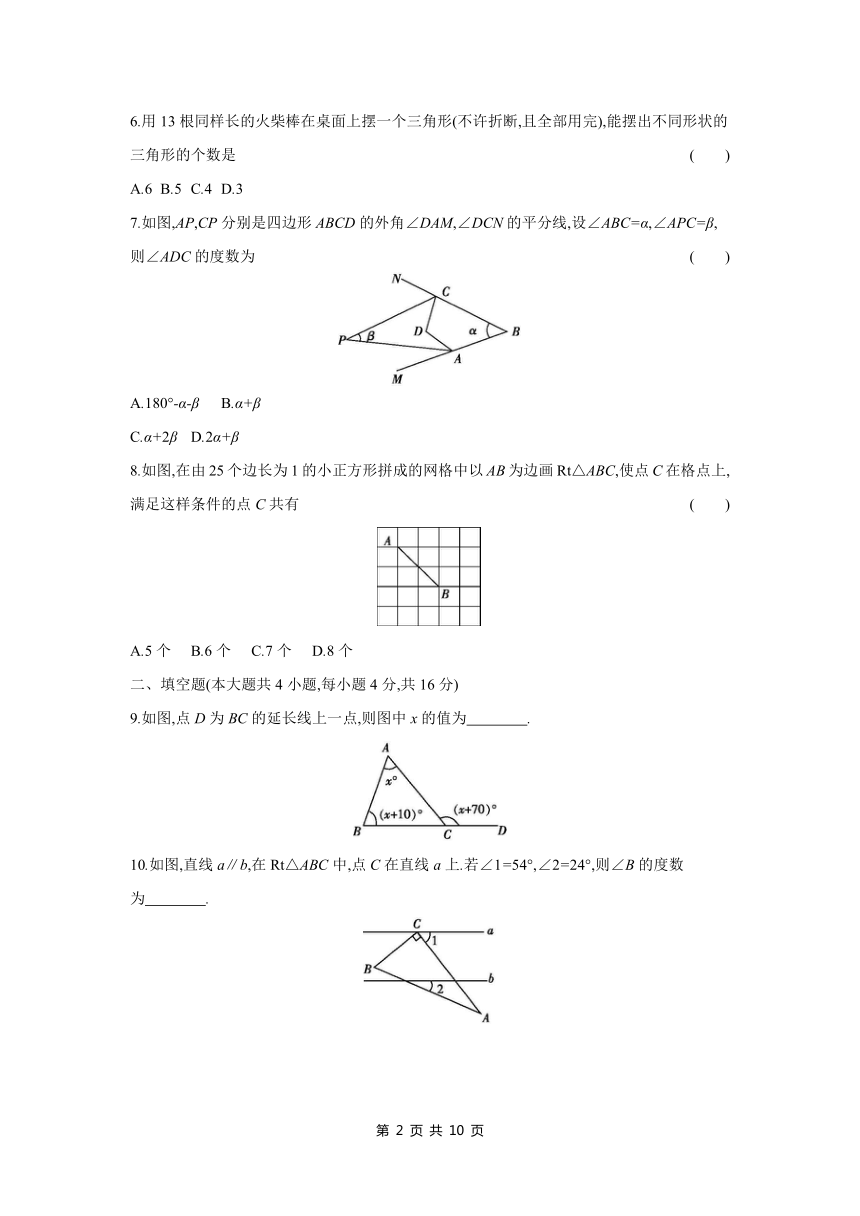
7.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为 ( )
A.180°-α-β B.α+β
C.α+2β D.2α+β
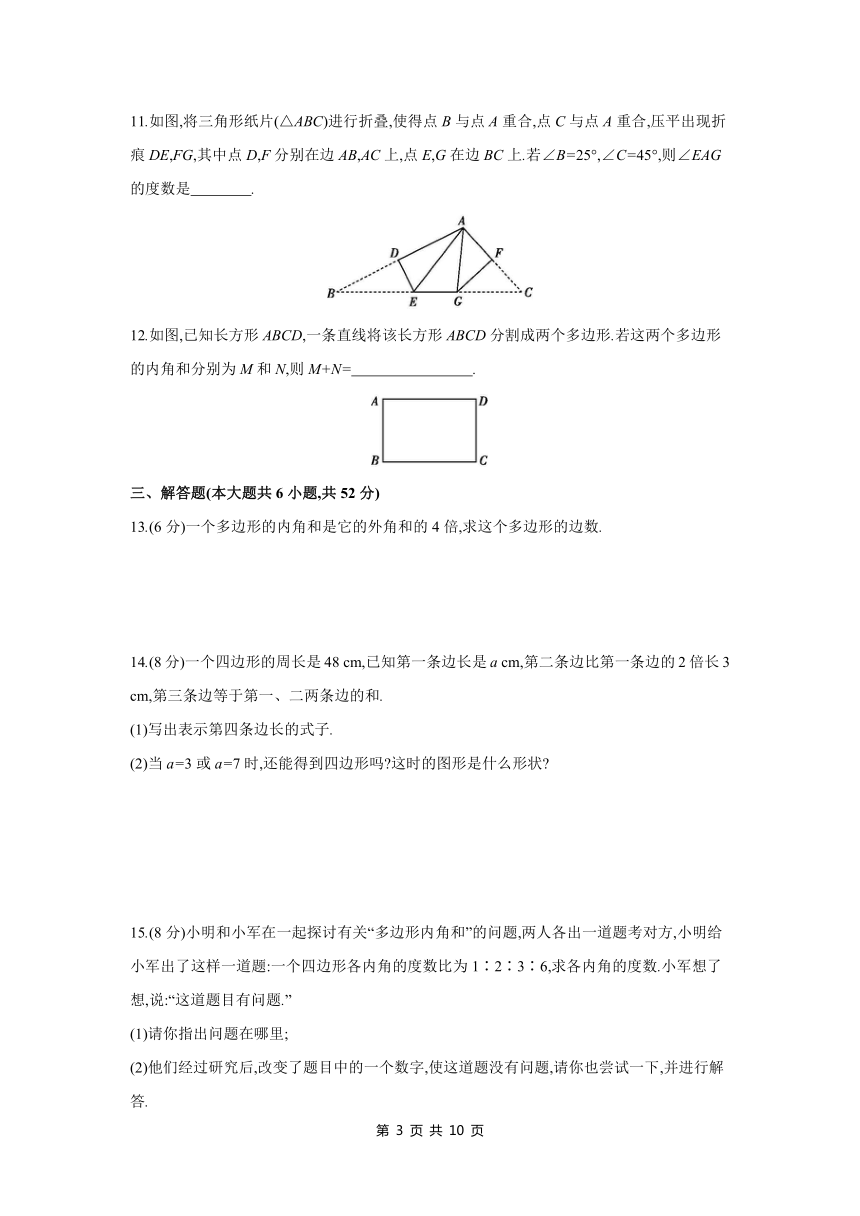
8.如图,在由25个边长为1的小正方形拼成的网格中以AB为边画Rt△ABC,使点C在格点上,满足这样条件的点C共有 ( )
A.5个 B.6个 C.7个 D.8个
二、填空题(本大题共4小题,每小题4分,共16分)
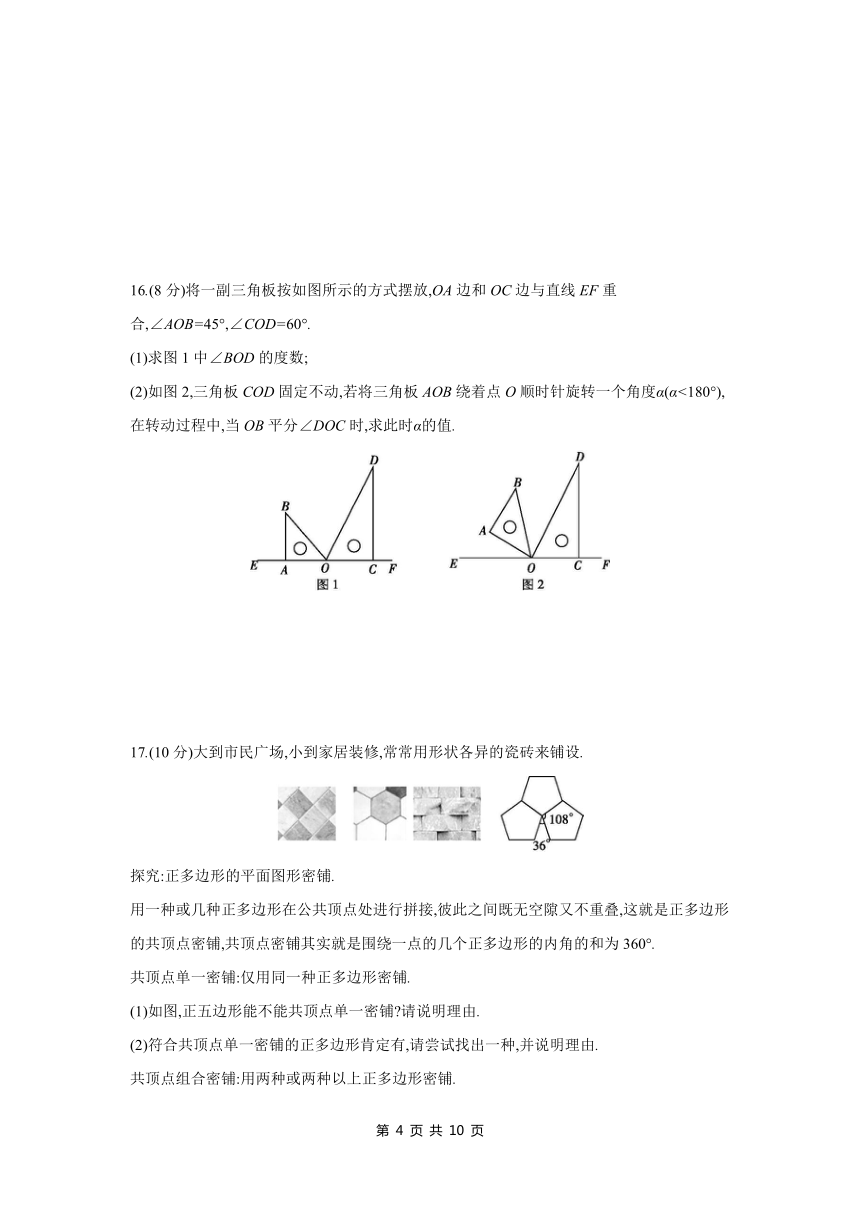
9.如图,点D为BC的延长线上一点,则图中x的值为 .
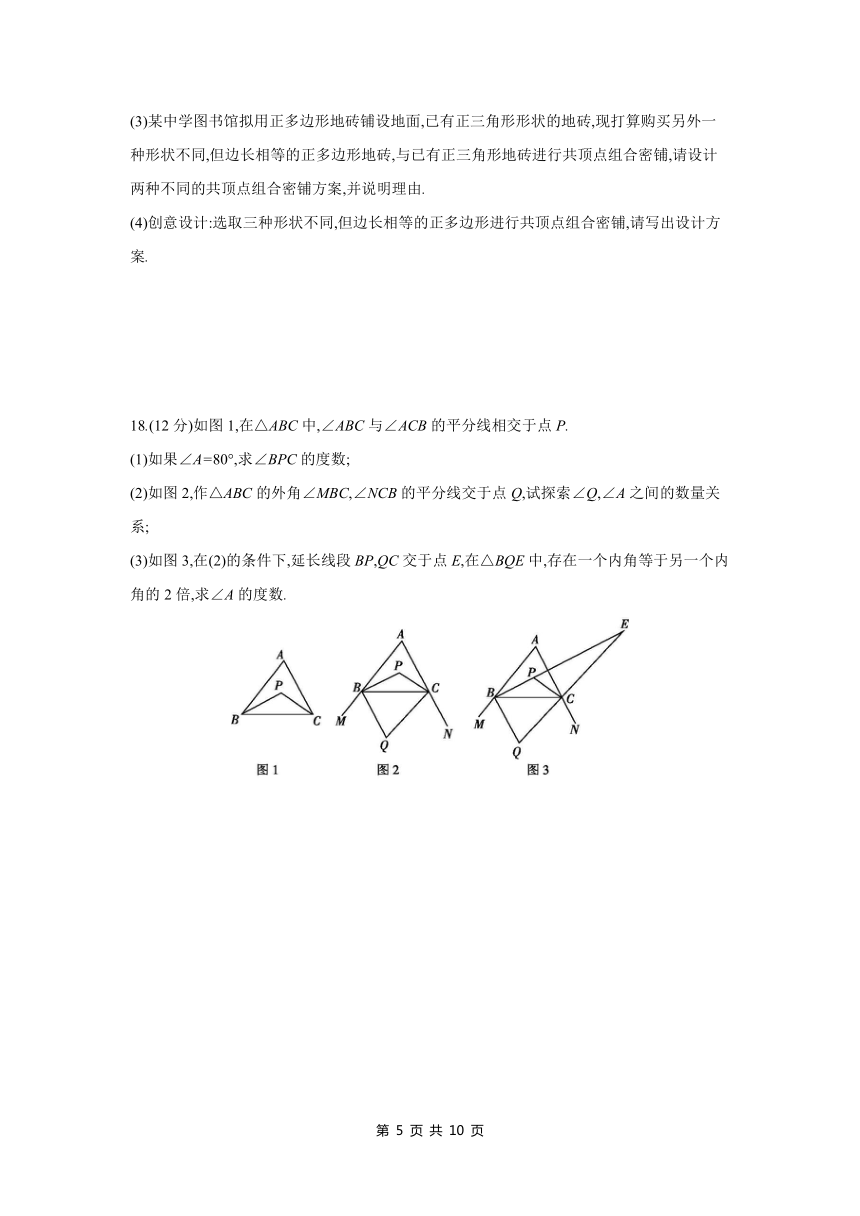
10.如图,直线a∥b,在Rt△ABC中,点C在直线a上.若∠1=54°,∠2=24°,则∠B的度数为 .
11.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中点D,F分别在边AB,AC上,点E,G在边BC上.若∠B=25°,∠C=45°,则∠EAG的度数是 .
12.如图,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N= .
三、解答题(本大题共6小题,共52分)
13.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
14.(8分)一个四边形的周长是48 cm,已知第一条边长是a cm,第二条边比第一条边的2倍长3 cm,第三条边等于第一、二两条边的和.
(1)写出表示第四条边长的式子.
(2)当a=3或a=7时,还能得到四边形吗 这时的图形是什么形状
15.(8分)小明和小军在一起探讨有关“多边形内角和”的问题,两人各出一道题考对方,小明给小军出了这样一道题:一个四边形各内角的度数比为1∶2∶3∶6,求各内角的度数.小军想了想,说:“这道题目有问题.”
(1)请你指出问题在哪里;
(2)他们经过研究后,改变了题目中的一个数字,使这道题没有问题,请你也尝试一下,并进行解答.
16.(8分)将一副三角板按如图所示的方式摆放,OA边和OC边与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数;
(2)如图2,三角板COD固定不动,若将三角板AOB绕着点O顺时针旋转一个角度α(α<180°),在转动过程中,当OB平分∠DOC时,求此时α的值.
17.(10分)大到市民广场,小到家居装修,常常用形状各异的瓷砖来铺设.
探究:正多边形的平面图形密铺.
用一种或几种正多边形在公共顶点处进行拼接,彼此之间既无空隙又不重叠,这就是正多边形的共顶点密铺,共顶点密铺其实就是围绕一点的几个正多边形的内角的和为360°.
共顶点单一密铺:仅用同一种正多边形密铺.
(1)如图,正五边形能不能共顶点单一密铺 请说明理由.
(2)符合共顶点单一密铺的正多边形肯定有,请尝试找出一种,并说明理由.
共顶点组合密铺:用两种或两种以上正多边形密铺.
(3)某中学图书馆拟用正多边形地砖铺设地面,已有正三角形形状的地砖,现打算购买另外一种形状不同,但边长相等的正多边形地砖,与已有正三角形地砖进行共顶点组合密铺,请设计两种不同的共顶点组合密铺方案,并说明理由.
(4)创意设计:选取三种形状不同,但边长相等的正多边形进行共顶点组合密铺,请写出设计方案.
18.(12分)如图1,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探索∠Q,∠A之间的数量关系;
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B D C A B B C D
1.B 解析:锐角三角形有三个锐角.
2.D 解析:共有6个,分别是△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.
解题思路 根据三角形的高的概念判断即可.
易错警示 有同学认为三角形的高一定是在三角形的内部,易忽视钝角三角形的高可以在三角形的外部而漏算△ACE,也可能忽视了直角三角形的高可以与边重合而漏写了以AD为直角边的直角三角形,即△ADB,△ADE,△ADC.
3.C 解析:设所求正多边形的边数为n,则60°·n=360°,解得n=6.
4.A 解析:∵三角形的三个内角的度数比为2∶3∶4,∴三个内角分别是180°×=40°,180°×=60°,180°×=80°,∴该三角形是锐角三角形.
5.B 解析:∵∠C=90°,∠CDA=70°,∴∠CAD=90°-∠CDA=20°,∵AD平分∠BAC,∴∠CAB=40°,∴∠B=90°-40°=50°.
6.B 解析:∵三角形两边之和大于第三边,∴只能有5种结果,即①1,6,6;②2,5,6;③3,5,5;④4,4,5;⑤3,4,6.
7.C 解析:在四边形ABCD中,∠ADC=360°-α-(∠DCB+∠DAB)=360°-α-(360°-2∠PCD-2∠PAD)=2(∠PCD+∠PAD)-α=2(∠ADC-β)-α,∴∠ADC=α+2β.
8.D 解析:如图,满足这样条件的点C共有8个.
二、填空题
9.60 解析:由三角形外角的性质,可得x+70=x+x+10,解得x=60.
10.60° 解析:如图,∵a∥b,∴∠1=∠3=54°,∵∠3=∠2+∠A,∴∠A=54°-24°=30°,∵∠ACB=90°,∴∠B=90°-30°=60°.
11.40° 解析:∵∠B=25°,∠C=45°,∴∠BAC=180°-25°-45°=110°,由折叠可得∠BAE=∠B=25°,∠CAG=∠C=45°,∴∠EAG=110°-(25°+45°)=40°.
12.360°或540°或720° 解析:不同的划分方法有4种,见图:
M+N不同的值有3种,分别是360°,540°和720°.
三、解答题
13.解:设这个多边形的边数为n. (1分)
依题意,得(n-2)×180=4×360,
解得n=10. (5分)
答:这个多边形的边数是10. (6分)
14.解:(1)第四条边长为(42-6a)cm. (4分)
(2)当a=3时,四条边的边长分别为3 cm,9 cm,12 cm,24 cm,
∵3+9+12=24,∴不是四边形,是一条线段; (6分)
当a=7时,四条边的边长分别为7 cm,17 cm,24 cm,0 cm,
显然,不是四边形,仍然是一条线段. (8分)
15.解:(1)根据题中条件可知,四边形中最大内角的度数为(4-2)×180°×=180°,
∵四边形的每一个内角都小于180°,
∴这个角不能是四边形的内角. (4分)
(2)答案不唯一,如将度数比改为1∶2∶3∶4即可.
∵四边形的内角和为360°,
∴四个内角分别为360°×=36°,360°×=72°,360°×=108°,360°×=144°. (8分)
16.解:(1)∵∠AOB+∠BOD+∠COD=180°,又∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°-∠AOB-∠COD=75°. (4分)
(2)如图,当OB平分∠DOC时,
∵∠DOC=60°,
∴∠DOB=∠BOC=30°,
∴∠BOE=150°.
∵∠BOA=45°,∴∠EOA=α=105°. (8分)
17.解:(1)设有x个正五边形.
∵正五边形的每一个内角为108°,
若想用x个108°围成360°,则108x=360.
解得x=(不符合题意).
∴正五边形不可以共顶点单一密铺. (2分)
(2)正方形可以共顶点单一密铺.
设有x个正方形.
∵正方形的每一个内角为90°,
若想用x个90°围成360°,则90x=360.
解得x=4.
∴正方形可以共顶点单一密铺. (4分)
(3)①正三角形与正方形可以共顶点组合密铺.
设有x个正三角形,y个正方形.
∵正三角形的每一个内角为60°,正方形的每一个内角是90°,
若想用x个60°与y个90°围成360°,
则60x+90y=360,即2x+3y=12,
这个二元一次方程的正整数解为x=3,y=2.
∴正三角形与正方形可以共顶点组合密铺. (6分)
②正三角形与正六边形可以共顶点组合密铺.
设有x个正三角形,y个正六边形.
∵正三角形的每一个内角为60°,正六边形的每一个内角是120°,
若想用x个60°与y个120°围成360°,
则60x+120y=360,即x+2y=6,
这个二元一次方程的正整数解为x=2,y=2或x=4,y=1,
∴正三角形与正六边形可以共顶点组合密铺. (8分)
(4)正三角形、正方形与正六边形可以共顶点组合密铺.
设有x个正三角形、y个正方形、z个正六边形,
∵正三角形的每一个内角为60°,正方形的每一个内角是90°,正六边形的每一个内角是120°,
若想用x个60°、y个90°与z个120°围成360°,
则60x+90y+120z=360,即2x+3y+4z=12.
这个三元一次方程的正整数解为x=1,y=2,z=1.
∴正三角形、正方形与正六边形可以共顶点组合密铺. (10分)
18.解:(1)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠BPC=180°-(∠ABC+∠ACB)=180°-×100°=130°. (2分)
(2)∵外角∠MBC,∠NCB的平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°-∠ABC-∠ACB)=(180°+∠A)=90°+∠A, (4分)
∴∠Q=180°-(90°+∠A)=90°-∠A. (5分)
(3)如图,延长BC至点F.
∵CQ为△ABC的外角∠NCB的平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°. (8分)
如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°-∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°. (12分)
解题思路 (1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠BPC即可解决问题.(2)根据三角形外角的性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求出∠CBQ+∠BCQ,最后根据三角形的内角和定理即可求解.(3)在△BQE中,由于∠Q=90°-∠A,求出∠E=∠A,∠EBQ=90°,所以如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q.分别列出方程,求解即可.
技巧点拨 我们常常会遇到确定两个角的平分线的夹角的度数问题,解此类问题的关键是识别好角平分线相交型的三个重要模型及其结论,这样可以帮助我们在解题时迅速找到思维的切入点,从而有效地打开解题通道.
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.关于三角形的三个内角,下列说法错误的是 ( )
A.必有一内角不小于60° B.最多有两个锐角
C.最少有两个锐角 D.必有一内角不大于60°
2.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E,HE是△AEC的中线,那么以AD为高的三角形有 ( )
A.2个 B.3个 C.5个 D.6个
3.若正多边形的一个外角是60°,则这个正多边形的边数是 ( )
A.4 B.5 C.6 D.7
4.若一个三角形的三个内角的度数比为2∶3∶4,则这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
5.如图,在△ABC中,∠C=90°,AD平分∠BAC,∠CDA=70°,则∠B的度数为( )
A.60° B.50° C.40° D.30°
6.用13根同样长的火柴棒在桌面上摆一个三角形(不许折断,且全部用完),能摆出不同形状的三角形的个数是 ( )
A.6 B.5 C.4 D.3
7.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为 ( )
A.180°-α-β B.α+β
C.α+2β D.2α+β
8.如图,在由25个边长为1的小正方形拼成的网格中以AB为边画Rt△ABC,使点C在格点上,满足这样条件的点C共有 ( )
A.5个 B.6个 C.7个 D.8个
二、填空题(本大题共4小题,每小题4分,共16分)
9.如图,点D为BC的延长线上一点,则图中x的值为 .
10.如图,直线a∥b,在Rt△ABC中,点C在直线a上.若∠1=54°,∠2=24°,则∠B的度数为 .
11.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中点D,F分别在边AB,AC上,点E,G在边BC上.若∠B=25°,∠C=45°,则∠EAG的度数是 .
12.如图,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N= .
三、解答题(本大题共6小题,共52分)
13.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
14.(8分)一个四边形的周长是48 cm,已知第一条边长是a cm,第二条边比第一条边的2倍长3 cm,第三条边等于第一、二两条边的和.
(1)写出表示第四条边长的式子.
(2)当a=3或a=7时,还能得到四边形吗 这时的图形是什么形状
15.(8分)小明和小军在一起探讨有关“多边形内角和”的问题,两人各出一道题考对方,小明给小军出了这样一道题:一个四边形各内角的度数比为1∶2∶3∶6,求各内角的度数.小军想了想,说:“这道题目有问题.”
(1)请你指出问题在哪里;
(2)他们经过研究后,改变了题目中的一个数字,使这道题没有问题,请你也尝试一下,并进行解答.
16.(8分)将一副三角板按如图所示的方式摆放,OA边和OC边与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数;
(2)如图2,三角板COD固定不动,若将三角板AOB绕着点O顺时针旋转一个角度α(α<180°),在转动过程中,当OB平分∠DOC时,求此时α的值.
17.(10分)大到市民广场,小到家居装修,常常用形状各异的瓷砖来铺设.
探究:正多边形的平面图形密铺.
用一种或几种正多边形在公共顶点处进行拼接,彼此之间既无空隙又不重叠,这就是正多边形的共顶点密铺,共顶点密铺其实就是围绕一点的几个正多边形的内角的和为360°.
共顶点单一密铺:仅用同一种正多边形密铺.
(1)如图,正五边形能不能共顶点单一密铺 请说明理由.
(2)符合共顶点单一密铺的正多边形肯定有,请尝试找出一种,并说明理由.
共顶点组合密铺:用两种或两种以上正多边形密铺.
(3)某中学图书馆拟用正多边形地砖铺设地面,已有正三角形形状的地砖,现打算购买另外一种形状不同,但边长相等的正多边形地砖,与已有正三角形地砖进行共顶点组合密铺,请设计两种不同的共顶点组合密铺方案,并说明理由.
(4)创意设计:选取三种形状不同,但边长相等的正多边形进行共顶点组合密铺,请写出设计方案.
18.(12分)如图1,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探索∠Q,∠A之间的数量关系;
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B D C A B B C D
1.B 解析:锐角三角形有三个锐角.
2.D 解析:共有6个,分别是△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.
解题思路 根据三角形的高的概念判断即可.
易错警示 有同学认为三角形的高一定是在三角形的内部,易忽视钝角三角形的高可以在三角形的外部而漏算△ACE,也可能忽视了直角三角形的高可以与边重合而漏写了以AD为直角边的直角三角形,即△ADB,△ADE,△ADC.
3.C 解析:设所求正多边形的边数为n,则60°·n=360°,解得n=6.
4.A 解析:∵三角形的三个内角的度数比为2∶3∶4,∴三个内角分别是180°×=40°,180°×=60°,180°×=80°,∴该三角形是锐角三角形.
5.B 解析:∵∠C=90°,∠CDA=70°,∴∠CAD=90°-∠CDA=20°,∵AD平分∠BAC,∴∠CAB=40°,∴∠B=90°-40°=50°.
6.B 解析:∵三角形两边之和大于第三边,∴只能有5种结果,即①1,6,6;②2,5,6;③3,5,5;④4,4,5;⑤3,4,6.
7.C 解析:在四边形ABCD中,∠ADC=360°-α-(∠DCB+∠DAB)=360°-α-(360°-2∠PCD-2∠PAD)=2(∠PCD+∠PAD)-α=2(∠ADC-β)-α,∴∠ADC=α+2β.
8.D 解析:如图,满足这样条件的点C共有8个.
二、填空题
9.60 解析:由三角形外角的性质,可得x+70=x+x+10,解得x=60.
10.60° 解析:如图,∵a∥b,∴∠1=∠3=54°,∵∠3=∠2+∠A,∴∠A=54°-24°=30°,∵∠ACB=90°,∴∠B=90°-30°=60°.
11.40° 解析:∵∠B=25°,∠C=45°,∴∠BAC=180°-25°-45°=110°,由折叠可得∠BAE=∠B=25°,∠CAG=∠C=45°,∴∠EAG=110°-(25°+45°)=40°.
12.360°或540°或720° 解析:不同的划分方法有4种,见图:
M+N不同的值有3种,分别是360°,540°和720°.
三、解答题
13.解:设这个多边形的边数为n. (1分)
依题意,得(n-2)×180=4×360,
解得n=10. (5分)
答:这个多边形的边数是10. (6分)
14.解:(1)第四条边长为(42-6a)cm. (4分)
(2)当a=3时,四条边的边长分别为3 cm,9 cm,12 cm,24 cm,
∵3+9+12=24,∴不是四边形,是一条线段; (6分)
当a=7时,四条边的边长分别为7 cm,17 cm,24 cm,0 cm,
显然,不是四边形,仍然是一条线段. (8分)
15.解:(1)根据题中条件可知,四边形中最大内角的度数为(4-2)×180°×=180°,
∵四边形的每一个内角都小于180°,
∴这个角不能是四边形的内角. (4分)
(2)答案不唯一,如将度数比改为1∶2∶3∶4即可.
∵四边形的内角和为360°,
∴四个内角分别为360°×=36°,360°×=72°,360°×=108°,360°×=144°. (8分)
16.解:(1)∵∠AOB+∠BOD+∠COD=180°,又∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°-∠AOB-∠COD=75°. (4分)
(2)如图,当OB平分∠DOC时,
∵∠DOC=60°,
∴∠DOB=∠BOC=30°,
∴∠BOE=150°.
∵∠BOA=45°,∴∠EOA=α=105°. (8分)
17.解:(1)设有x个正五边形.
∵正五边形的每一个内角为108°,
若想用x个108°围成360°,则108x=360.
解得x=(不符合题意).
∴正五边形不可以共顶点单一密铺. (2分)
(2)正方形可以共顶点单一密铺.
设有x个正方形.
∵正方形的每一个内角为90°,
若想用x个90°围成360°,则90x=360.
解得x=4.
∴正方形可以共顶点单一密铺. (4分)
(3)①正三角形与正方形可以共顶点组合密铺.
设有x个正三角形,y个正方形.
∵正三角形的每一个内角为60°,正方形的每一个内角是90°,
若想用x个60°与y个90°围成360°,
则60x+90y=360,即2x+3y=12,
这个二元一次方程的正整数解为x=3,y=2.
∴正三角形与正方形可以共顶点组合密铺. (6分)
②正三角形与正六边形可以共顶点组合密铺.
设有x个正三角形,y个正六边形.
∵正三角形的每一个内角为60°,正六边形的每一个内角是120°,
若想用x个60°与y个120°围成360°,
则60x+120y=360,即x+2y=6,
这个二元一次方程的正整数解为x=2,y=2或x=4,y=1,
∴正三角形与正六边形可以共顶点组合密铺. (8分)
(4)正三角形、正方形与正六边形可以共顶点组合密铺.
设有x个正三角形、y个正方形、z个正六边形,
∵正三角形的每一个内角为60°,正方形的每一个内角是90°,正六边形的每一个内角是120°,
若想用x个60°、y个90°与z个120°围成360°,
则60x+90y+120z=360,即2x+3y+4z=12.
这个三元一次方程的正整数解为x=1,y=2,z=1.
∴正三角形、正方形与正六边形可以共顶点组合密铺. (10分)
18.解:(1)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠BPC=180°-(∠ABC+∠ACB)=180°-×100°=130°. (2分)
(2)∵外角∠MBC,∠NCB的平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°-∠ABC-∠ACB)=(180°+∠A)=90°+∠A, (4分)
∴∠Q=180°-(90°+∠A)=90°-∠A. (5分)
(3)如图,延长BC至点F.
∵CQ为△ABC的外角∠NCB的平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°. (8分)
如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°-∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°. (12分)
解题思路 (1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠BPC即可解决问题.(2)根据三角形外角的性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求出∠CBQ+∠BCQ,最后根据三角形的内角和定理即可求解.(3)在△BQE中,由于∠Q=90°-∠A,求出∠E=∠A,∠EBQ=90°,所以如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q.分别列出方程,求解即可.
技巧点拨 我们常常会遇到确定两个角的平分线的夹角的度数问题,解此类问题的关键是识别好角平分线相交型的三个重要模型及其结论,这样可以帮助我们在解题时迅速找到思维的切入点,从而有效地打开解题通道.
