第9章 轴对称、平移与旋转 基础过关测试卷(含答案) 2024-2025学年华东师大版七年级数学下册
文档属性
| 名称 | 第9章 轴对称、平移与旋转 基础过关测试卷(含答案) 2024-2025学年华东师大版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 10:54:36 | ||
图片预览



文档简介
第9章 轴对称、平移与旋转
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.京剧被誉为我国国粹,为传承民族文化,某中学开展了“京剧进课堂”的实践活动,学生们制作了各式各样的脸谱.下列脸谱中,不是轴对称图形的是 ( )
2.下列图案中,能通过左边图案平移得到的是 ( )
3.下列图形中,是中心对称图形的是 ( )
4.下列图形中,是全等图形的是 ( )
A.①和② B.③和④ C.①和③ D.②和③
5.下列图形中,对称轴条数最多的是 ( )
6.如图,已知图中的两个三角形全等,则∠1的度数为 ( )
A.72° B.60° C.50° D.58°
7.如图,将一块含30°角的直角三角板ABC绕点C顺时针旋转到△A'B'C,当点B,C,A'在同一条直线上时,三角板ABC旋转的角度为 ( )
A.150° B.120° C.60° D.30°
8.如图,将周长为12 cm的△ABC沿BC方向向右平移3 cm得到△DEF,则四边形ABFD的周长为 ( )
A.24 cm B.21 cm C.18 cm D.15 cm
二、填空题(本大题共4小题,每小题4分,共16分)
9.某同学从平面镜里看到镜子对面的电子钟的示数如图所示,这时的实际时间是 .
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得到∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的度数是 .
11.如图,已知△ABC≌△ADE,∠A=120°,∠ABC=20°,则∠BOD= .
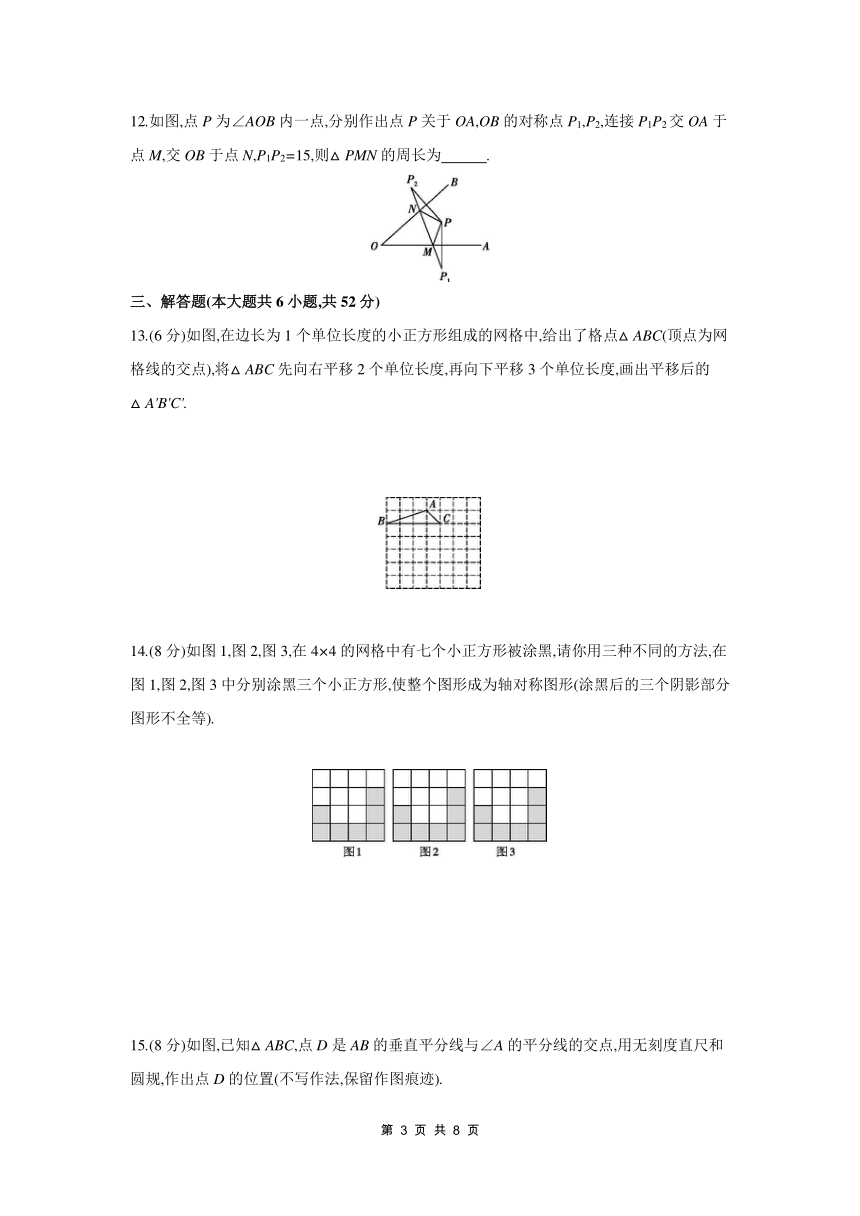
12.如图,点P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,P1P2=15,则△PMN的周长为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点),将△ABC先向右平移2个单位长度,再向下平移3个单位长度,画出平移后的△A'B'C'.
14.(8分)如图1,图2,图3,在4×4的网格中有七个小正方形被涂黑,请你用三种不同的方法,在图1,图2,图3中分别涂黑三个小正方形,使整个图形成为轴对称图形(涂黑后的三个阴影部分图形不全等).
15.(8分)如图,已知△ABC,点D是AB的垂直平分线与∠A的平分线的交点,用无刻度直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).
16.(8分)如图,在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
17.(10分)如图,已知△ABC≌△ADE,其中点B和点D是对应点,点C和点E是对应点.
(1)写出对应边和对应角.
(2)∠BAD和∠CAE相等吗 请说明理由.
18.(12分)如图,将线段AB向右平移至线段DC,使点A与点D对应,点B与点C对应,连接AD,BC,∠A=2∠B.
(1)求∠BCD的度数;
(2)若点F,G,E依次为BC的延长线上的点,且∠EFD=∠EDF,∠FDG=30°,请判断DG是否平分∠CDE,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B C D B A D A C
1.B 解析:A,C,D左右对称,是轴对称图形,B不是轴对称图形.
2.C 解析:通过平移得到的图案,形状必须与原图案相同,角度也必须与原图案相同,观察图形可知选C.
3.D
4.B 解析:③和④可以完全重合,因此是全等图形的是③和④.
5.A 解析:选项A有无数条对称轴;选项B有五条对称轴;选项C有三条对称轴;选项D有四条对称轴.
6.D 解析:∵∠1是三角形a,c两边的夹角,根据全等三角形的性质可得∠1=180°-50°-72°=58°.
7.A 解析:∵将一块含30°角的直角三角板ABC绕点C顺时针旋转到△A'B'C,∴BC与B'C是对应边,∴旋转角∠BCB'=180°-30°=150°.
8.C 解析:∵将周长为12 cm的△ABC沿BC方向向右平移3 cm得到△DEF,∴DF=AC,AD=CF=3 cm,∴四边形ABFD的周长=AB+BF+DF+AD=AB+BC+CF+AC+AD=△ABC的周长+AD+CF=12+3+3=18(cm).
二、填空题
9.10:51 解析:∵是从平面镜看,∴对称轴为竖直方向的直线,∵2的对称数字是5,平面镜中数字的顺序与实际数字的顺序相反,∴这时的实际时间是10:51.
10.105° 解析:∵把∠AOB沿着MN的方向平移一定距离后得到∠CPD,∴BO∥DP,∴∠BON=∠DPN=50°,∵∠AOM+∠AOB+∠BON=180°,∴∠AOB=180°-25°-50°=105°.
11.160° 解析:∵△ABC≌△ADE,∠ABC=20°,∴∠ADE=20°,由外角的性质可知∠BOD=∠ADE+∠BCD=∠ADE+∠ABC+∠A=20°+20°+120°=160°.
12.15 解析:∵点P关于OA的对称点是P1,点P关于OB的对称点是P2,∴PM=P1M,PN=P2N,∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15.
三、解答题
13.解:如图所示,△A'B'C'为所求. (6分)
14.解:答案不唯一,如图所示. (8分)
15.解:如图所示,点D为所求. (8分)
要点归纳 1.利用尺规作线段AB的垂直平分线的方法:(1)分别以点A和B为圆心、相同长(大于线段AB长的一半)为半径作弧,两弧分别相交于点P和点Q;(2)作直线PQ.直线PQ就是所要求作的线段AB的垂直平分线.
2.利用尺规作∠AOB的平分线的方法:(1)以点O为圆心、任意长为半径作弧,与角的两边分别交于M,N两点;(2)分别以点M和N为圆心、相同长(大于线段MN长的一半)为半径作弧,在∠AOB内,两弧相交于点P;(3)作射线OP.射线OP就是所要求作的∠AOB的平分线.
16.解:(1)在△ABC中,∵∠B+∠ACB=30°,∴∠BAC=150°. (2分)
∵△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,旋转角为∠BAD,∴旋转角的度数为150°. (4分)
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AD=AB=4,AC=AE,
∴∠BAE=360°-150°-150°=60°, (7分)
∵点C为AD的中点,∴AC=AD=2,∴AE=2. (8分)
17.解:(1)对应边是AB和AD,AC和AE,BC和DE;
对应角是∠BAC与∠DAE,∠B和∠D,∠C和∠E. (5分)
(2)∠BAD=∠CAE,理由如下:
∵△ABC≌△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE. (10分)
18.解:(1)由平移的性质,得AB∥DC,AD∥BC,
∴∠B+∠BCD=180°,∠A+∠B=180°.
∵∠A=2∠B,∴∠B=60°,∴∠BCD=180°-60°=120°. (4分)
(2)DG平分∠CDE. (5分)
理由:∵AB∥DC,∴∠DCE=∠B=60°.
由三角形外角的性质,得∠CDF=∠DFE-60°,
∵∠FDG=30°,∴∠CDG=∠CDF+30°=∠DFE-60°+30°=∠DFE-30°,
∵∠EDG=∠EDF-∠FDG=∠EDF-30°,
又∵∠DFE=∠EDF,∴∠CDG=∠EDG,∴DG平分∠CDE. (12分)
思路点拨 “线段AB向右平移至线段DC”这里隐含的条件为AB∥DC,AD∥BC,利用平行线的性质,得出∠A+∠B=180°,结合题目已给的条件∠A=2∠B,即可解出一些角度,从而解决问题(1);问题(2)这种判断题,适合条件与结论双向推理,可以先逆向推理得出∠GDE的一些信息,得出∠GDE=∠FDE-∠GDF=∠FDE-30°=∠DFE-30°,接下来的目的就是寻找∠DFE与∠CDG的关系了,这时需顺向推理,结合三角形的外角性质和问题(1)得出的结论,得出∠CDG=∠CDF+∠FDG=∠CDF+30°=∠DFE-∠DCF+30°=∠DFE-30°,从而推出∠GDE=∠CDG,即可判断是平分.
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.京剧被誉为我国国粹,为传承民族文化,某中学开展了“京剧进课堂”的实践活动,学生们制作了各式各样的脸谱.下列脸谱中,不是轴对称图形的是 ( )
2.下列图案中,能通过左边图案平移得到的是 ( )
3.下列图形中,是中心对称图形的是 ( )
4.下列图形中,是全等图形的是 ( )
A.①和② B.③和④ C.①和③ D.②和③
5.下列图形中,对称轴条数最多的是 ( )
6.如图,已知图中的两个三角形全等,则∠1的度数为 ( )
A.72° B.60° C.50° D.58°
7.如图,将一块含30°角的直角三角板ABC绕点C顺时针旋转到△A'B'C,当点B,C,A'在同一条直线上时,三角板ABC旋转的角度为 ( )
A.150° B.120° C.60° D.30°
8.如图,将周长为12 cm的△ABC沿BC方向向右平移3 cm得到△DEF,则四边形ABFD的周长为 ( )
A.24 cm B.21 cm C.18 cm D.15 cm
二、填空题(本大题共4小题,每小题4分,共16分)
9.某同学从平面镜里看到镜子对面的电子钟的示数如图所示,这时的实际时间是 .
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得到∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的度数是 .
11.如图,已知△ABC≌△ADE,∠A=120°,∠ABC=20°,则∠BOD= .
12.如图,点P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,P1P2=15,则△PMN的周长为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点),将△ABC先向右平移2个单位长度,再向下平移3个单位长度,画出平移后的△A'B'C'.
14.(8分)如图1,图2,图3,在4×4的网格中有七个小正方形被涂黑,请你用三种不同的方法,在图1,图2,图3中分别涂黑三个小正方形,使整个图形成为轴对称图形(涂黑后的三个阴影部分图形不全等).
15.(8分)如图,已知△ABC,点D是AB的垂直平分线与∠A的平分线的交点,用无刻度直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).
16.(8分)如图,在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
17.(10分)如图,已知△ABC≌△ADE,其中点B和点D是对应点,点C和点E是对应点.
(1)写出对应边和对应角.
(2)∠BAD和∠CAE相等吗 请说明理由.
18.(12分)如图,将线段AB向右平移至线段DC,使点A与点D对应,点B与点C对应,连接AD,BC,∠A=2∠B.
(1)求∠BCD的度数;
(2)若点F,G,E依次为BC的延长线上的点,且∠EFD=∠EDF,∠FDG=30°,请判断DG是否平分∠CDE,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B C D B A D A C
1.B 解析:A,C,D左右对称,是轴对称图形,B不是轴对称图形.
2.C 解析:通过平移得到的图案,形状必须与原图案相同,角度也必须与原图案相同,观察图形可知选C.
3.D
4.B 解析:③和④可以完全重合,因此是全等图形的是③和④.
5.A 解析:选项A有无数条对称轴;选项B有五条对称轴;选项C有三条对称轴;选项D有四条对称轴.
6.D 解析:∵∠1是三角形a,c两边的夹角,根据全等三角形的性质可得∠1=180°-50°-72°=58°.
7.A 解析:∵将一块含30°角的直角三角板ABC绕点C顺时针旋转到△A'B'C,∴BC与B'C是对应边,∴旋转角∠BCB'=180°-30°=150°.
8.C 解析:∵将周长为12 cm的△ABC沿BC方向向右平移3 cm得到△DEF,∴DF=AC,AD=CF=3 cm,∴四边形ABFD的周长=AB+BF+DF+AD=AB+BC+CF+AC+AD=△ABC的周长+AD+CF=12+3+3=18(cm).
二、填空题
9.10:51 解析:∵是从平面镜看,∴对称轴为竖直方向的直线,∵2的对称数字是5,平面镜中数字的顺序与实际数字的顺序相反,∴这时的实际时间是10:51.
10.105° 解析:∵把∠AOB沿着MN的方向平移一定距离后得到∠CPD,∴BO∥DP,∴∠BON=∠DPN=50°,∵∠AOM+∠AOB+∠BON=180°,∴∠AOB=180°-25°-50°=105°.
11.160° 解析:∵△ABC≌△ADE,∠ABC=20°,∴∠ADE=20°,由外角的性质可知∠BOD=∠ADE+∠BCD=∠ADE+∠ABC+∠A=20°+20°+120°=160°.
12.15 解析:∵点P关于OA的对称点是P1,点P关于OB的对称点是P2,∴PM=P1M,PN=P2N,∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15.
三、解答题
13.解:如图所示,△A'B'C'为所求. (6分)
14.解:答案不唯一,如图所示. (8分)
15.解:如图所示,点D为所求. (8分)
要点归纳 1.利用尺规作线段AB的垂直平分线的方法:(1)分别以点A和B为圆心、相同长(大于线段AB长的一半)为半径作弧,两弧分别相交于点P和点Q;(2)作直线PQ.直线PQ就是所要求作的线段AB的垂直平分线.
2.利用尺规作∠AOB的平分线的方法:(1)以点O为圆心、任意长为半径作弧,与角的两边分别交于M,N两点;(2)分别以点M和N为圆心、相同长(大于线段MN长的一半)为半径作弧,在∠AOB内,两弧相交于点P;(3)作射线OP.射线OP就是所要求作的∠AOB的平分线.
16.解:(1)在△ABC中,∵∠B+∠ACB=30°,∴∠BAC=150°. (2分)
∵△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,旋转角为∠BAD,∴旋转角的度数为150°. (4分)
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AD=AB=4,AC=AE,
∴∠BAE=360°-150°-150°=60°, (7分)
∵点C为AD的中点,∴AC=AD=2,∴AE=2. (8分)
17.解:(1)对应边是AB和AD,AC和AE,BC和DE;
对应角是∠BAC与∠DAE,∠B和∠D,∠C和∠E. (5分)
(2)∠BAD=∠CAE,理由如下:
∵△ABC≌△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE. (10分)
18.解:(1)由平移的性质,得AB∥DC,AD∥BC,
∴∠B+∠BCD=180°,∠A+∠B=180°.
∵∠A=2∠B,∴∠B=60°,∴∠BCD=180°-60°=120°. (4分)
(2)DG平分∠CDE. (5分)
理由:∵AB∥DC,∴∠DCE=∠B=60°.
由三角形外角的性质,得∠CDF=∠DFE-60°,
∵∠FDG=30°,∴∠CDG=∠CDF+30°=∠DFE-60°+30°=∠DFE-30°,
∵∠EDG=∠EDF-∠FDG=∠EDF-30°,
又∵∠DFE=∠EDF,∴∠CDG=∠EDG,∴DG平分∠CDE. (12分)
思路点拨 “线段AB向右平移至线段DC”这里隐含的条件为AB∥DC,AD∥BC,利用平行线的性质,得出∠A+∠B=180°,结合题目已给的条件∠A=2∠B,即可解出一些角度,从而解决问题(1);问题(2)这种判断题,适合条件与结论双向推理,可以先逆向推理得出∠GDE的一些信息,得出∠GDE=∠FDE-∠GDF=∠FDE-30°=∠DFE-30°,接下来的目的就是寻找∠DFE与∠CDG的关系了,这时需顺向推理,结合三角形的外角性质和问题(1)得出的结论,得出∠CDG=∠CDF+∠FDG=∠CDF+30°=∠DFE-∠DCF+30°=∠DFE-30°,从而推出∠GDE=∠CDG,即可判断是平分.
