第9章 轴对称、平移与旋转 能力提优测试卷(含答案) 2024-2025学年华东师大版七年级数学下册
文档属性
| 名称 | 第9章 轴对称、平移与旋转 能力提优测试卷(含答案) 2024-2025学年华东师大版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 10:55:00 | ||
图片预览


文档简介
第9章 轴对称、平移与旋转
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
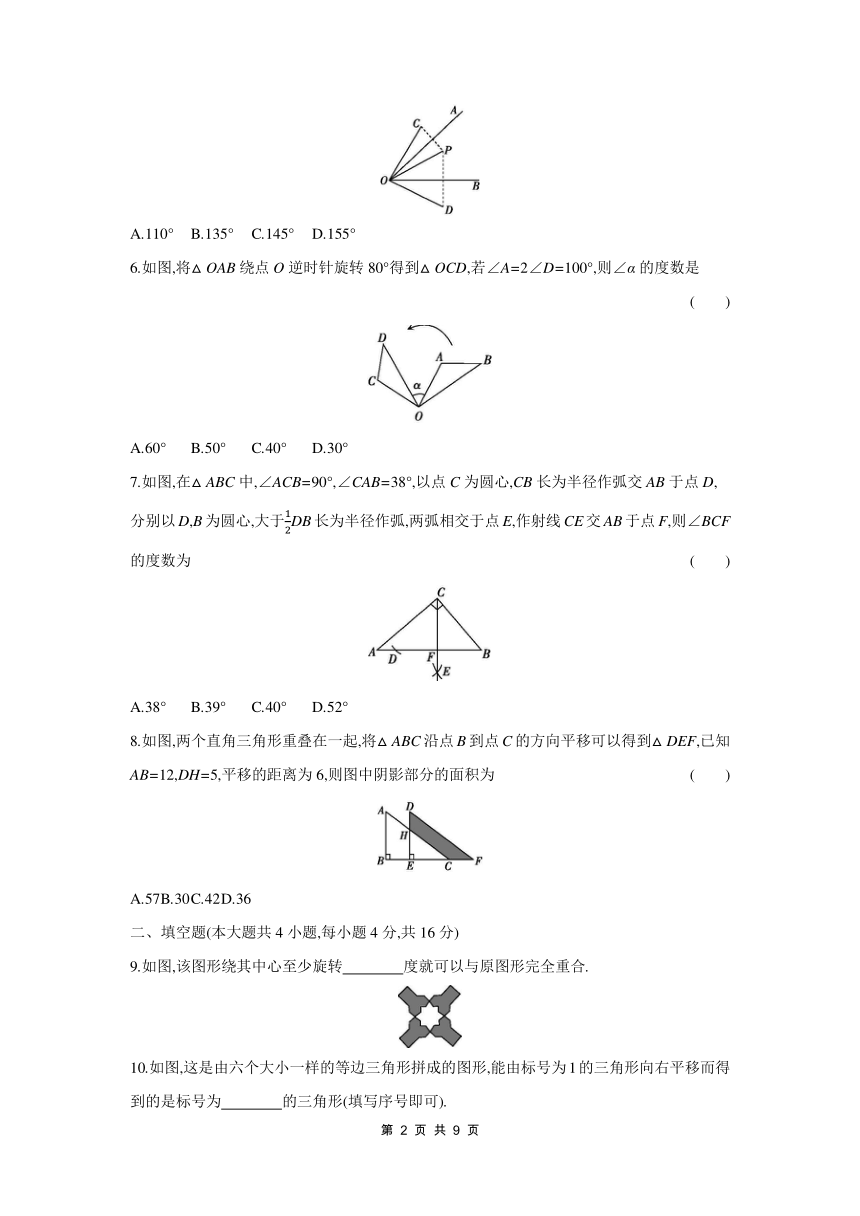
1.第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行,如图所示的巴黎奥运会项目图标中,既是轴对称图形又是中心对称图形的是 ( )
2.对折一张长方形的纸,然后用笔尖在上面扎出“B”,再把它打开铺平,你可见到 ( )
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 ( )
A.点A与点A'是对称点 B.BO=B'O
C.∠AOB=∠A'OB' D.∠ACB=∠C'A'B'
4.下列说法正确的是 ( )
A.两个等腰三角形一定全等
B.形状相同的两个三角形全等
C.周长相等的两个三角形全等
D.全等三角形的周长一定相等
5.如图,点P为∠AOB内一点,分别作点P关于直线OA,OB的对称点C,D,若∠COD=70°,则∠CPD的度数是 ( )
A.110° B.135° C.145° D.155°
6.如图,将△OAB绕点O逆时针旋转80°得到△OCD,若∠A=2∠D=100°,则∠α的度数是 ( )
A.60° B.50° C.40° D.30°
7.如图,在△ABC中,∠ACB=90°,∠CAB=38°,以点C为圆心,CB长为半径作弧交AB于点D,分别以D,B为圆心,大于DB长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则∠BCF的度数为 ( )
A.38° B.39° C.40° D.52°
8.如图,两个直角三角形重叠在一起,将△ABC沿点B到点C的方向平移可以得到△DEF,已知AB=12,DH=5,平移的距离为6,则图中阴影部分的面积为 ( )
A.57 B.30 C.42 D.36
二、填空题(本大题共4小题,每小题4分,共16分)
9.如图,该图形绕其中心至少旋转 度就可以与原图形完全重合.
10.如图,这是由六个大小一样的等边三角形拼成的图形,能由标号为1的三角形向右平移而得到的是标号为 的三角形(填写序号即可).
11.如图,△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是 .
12.折纸是一门古老而有趣的艺术,现代数学家藤田文章和羽鸟公士郎甚至为折纸建立了一套完整的“折纸几何学公理”.如图,南南在课余时间拿出一张长方形纸片ABCD(∠A=∠B=∠C=∠D=90°),他先将纸片沿EF折叠,再将折叠后的纸片沿GH折叠,使得GD'与A'B'在同一条直线上,展开纸片后测量发现∠BFE=60°,则∠DGH= °.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,△ABC绕着顶点A逆时针旋转得到△ADE,∠B=40°,∠E=60°,AB∥DE,求∠DAC的度数.
14.(8分)如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE 请说明理由.
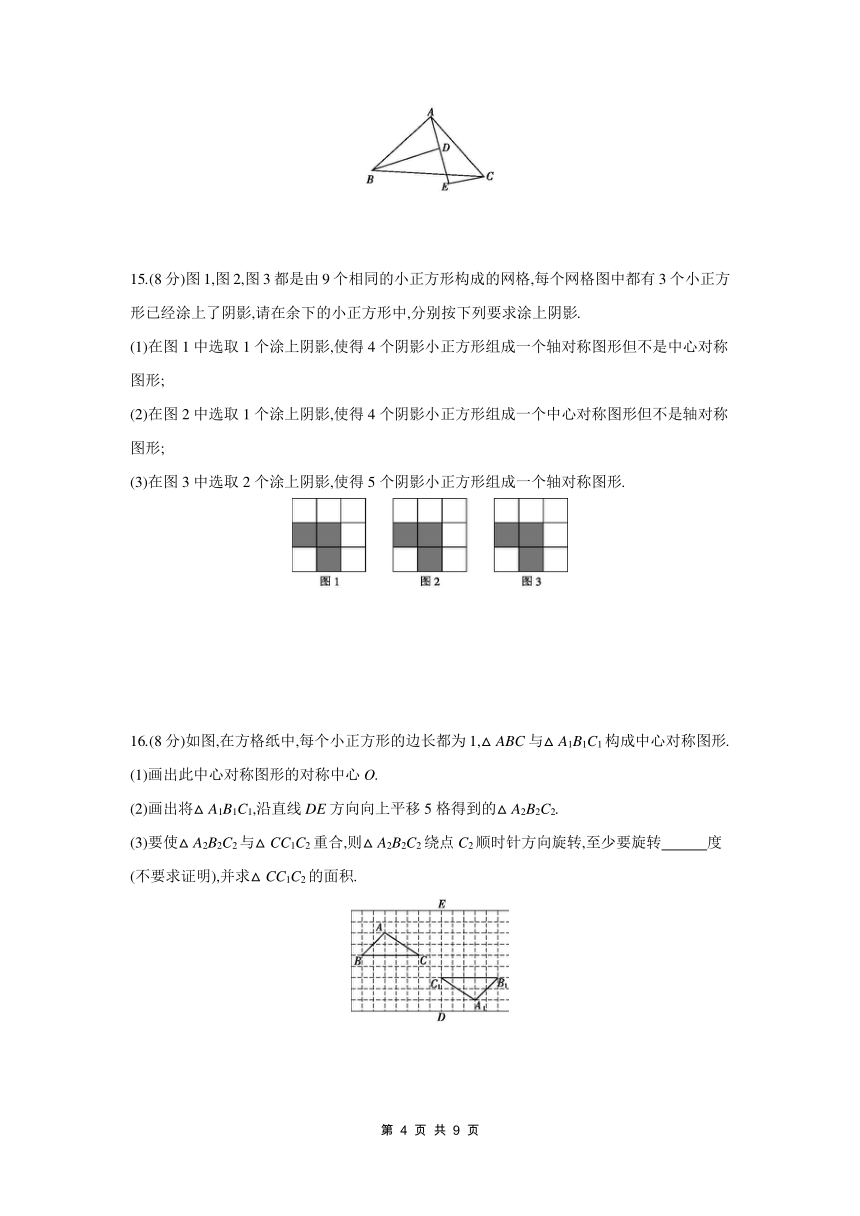
15.(8分)图1,图2,图3都是由9个相同的小正方形构成的网格,每个网格图中都有3个小正方形已经涂上了阴影,请在余下的小正方形中,分别按下列要求涂上阴影.
(1)在图1中选取1个涂上阴影,使得4个阴影小正方形组成一个轴对称图形但不是中心对称图形;
(2)在图2中选取1个涂上阴影,使得4个阴影小正方形组成一个中心对称图形但不是轴对称图形;
(3)在图3中选取2个涂上阴影,使得5个阴影小正方形组成一个轴对称图形.
16.(8分)如图,在方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成中心对称图形.
(1)画出此中心对称图形的对称中心O.
(2)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2.
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转 度(不要求证明),并求△CC1C2的面积.
17.(10分)某公园有很多的长方形草地,草地里修了很多有趣的小路,这些草地都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路(FF1=EE1=1),长方形除去阴影部分后剩余部分为草坪,则草坪的面积为 .
(2)如图2,有两条宽均为1米的小路(图中阴影部分),其余部分为草坪,求草坪的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
18.(12分)如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)观察猜想:
将图1中的三角板OCD沿AB的方向平移至图2的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN的度数是 .
(2)操作探究:
将图1中的三角板OCD绕点O按顺时针方向旋转,使边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数.
(3)深化拓展:
将图1中的三角板OCD绕点O按顺时针方向旋转一周,在旋转的过程中,当边OC旋转多少度时,边CD恰好与边MN平行
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C D D C B A A
1.D 解析:A.图形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;B.图形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;C.图形是中心对称图形,但不是轴对称图形,故本选项不符合题意;D.图形既是中心对称图形,也是轴对称图形,故本选项符合题意.
2.C 解析:根据对折之后打开铺平可知,折痕左右的图案是关于折痕成轴对称,观察选项可得只有C选项符合.
3.D 解析:∵△ABC与△A'B'C'关于点O成中心对称,∴点A与点A'是对称点,BO=B'O,∠AOB=∠A'OB',∴A,B,C选项都不符合题意,∵∠ACB与∠C'A'B'不是对应角,∴∠ACB=∠C'A'B'不成立,D选项符合题意.
4.D 解析:A.两个等腰三角形不一定全等,所以此选项不符合题意;B.形状相同的两个三角形不一定全等,所以此选项不符合题意;C.周长相等的两个三角形不一定全等,所以此选项不符合题意;D.全等三角形的周长一定相等,所以此选项符合题意.
5.C 解析:根据对称知,∠C=∠OPC,∠D=∠OPD.∵∠COD=70°,∴∠C+∠D=∠CPD=×(360°-70°)=145°.
6.B 解析:∵将△OAB绕点O逆时针旋转80°,∴∠A=∠C,∠AOC=80°,∴∠DOC=80°-α,∵∠A=2∠D=100°,∴∠D=50°,∴∠C+∠D+∠DOC=180°,∴100°+50°+80°-α=180°,解得α=50°.
7.A 解析:∵∠ACB=90°,∠CAB=38°,∴∠B=90°-∠CAB=52°,由作图可知,CE⊥AB,∴∠BCF=90°-∠B=38°.
8.A 解析:∵将△ABC沿点B到点C的方向平移可以得到△DEF,∴S△ABC=S△DEF,∴S阴影+S△EHC=S梯形ABEH+S△EHC,∴S阴影=S梯形ABEH=×(AB+EH)×BE=×(12+12-5)×6=57.
二、填空题
9.90 解析:把图形中的每个阴影部分与相邻的空白部分当作一个部分,因而整个圆周被分成4个完全相同的部分,每个部分对应的圆心角是360°÷4=90°,因而最少旋转的度数是90°.
10.5 解析:图中标号为5的三角形可由标号为1的三角形向右平移而得到.
11.4 解析:依题意有△DOC的面积等于△AOB的面积,等于6,CD=AB=3,根据三角形的面积公式,得CD边上的高为6×2÷3=4.
12.15 解析:由折叠得,∠AEF=∠A'EF,∠D=∠D'=90°,∠A=∠A'=90°,∠DGH=∠D'GH,∵ABCD是长方形,∠BFE=60°,∴AD∥BC,∴∠AEF+∠BFE=180°,∠GEF=∠BFE=60°,∴∠AEF=120°,∴∠A'EF=120°,∴∠A'EG=∠A'EF-∠GEF=60°,∴∠A'GE=30°,∵GD'与A'B'在同一条直线上,∴∠DGD'=∠A'GE=30°,∴∠DGH=∠DGD'=15°.
三、解答题
13.解:∵△ABC绕着顶点A逆时针旋转得到△ADE,
∴△ABC≌△ADE,
∴∠C=∠E=60°,∠D=∠B=40°,
∴∠BAC=180°-40°-60°=80°,
∵AB∥DE,
∴∠BAD=∠D=40°,
∴∠DAC=∠BAC-∠BAD=80°-40°=40°,
∴∠DAC的度数为40°. (6分)
14.解:(1)证明:∵△BAD≌△ACE,
∴BD=AE,AD=CE.
∴BD=AE=AD+DE=CE+DE,即BD=DE+CE. (4分)
(2)当△ABD满足∠ADB=90°时,BD∥CE. (5分)
理由:当∠ADB=90°时,∠BDE=180°-∠ADB=90°.
∵△BAD≌△ACE,∴∠E=∠ADB=90°,
∴∠BDE=∠E,
∴BD∥CE. (8分)
命题分析 这道题目的关键在于理解全等三角形的性质和平行线的判定方法.问题(1)的证明相对直接,只需要利用全等三角形的性质和线段的和差关系,关键找准对应线段;问题(2)的证明需要更多的几何知识,特别是角度的性质和平行线的判定,这里利用的是内错角相等,两直线平行这个判定.
15.解:(1)如图1所示(答案不唯一); (2分)
(2)如图2所示(答案不唯一); (5分)
(3)如图3所示(答案不唯一). (8分)
16.解:(1)如图,点O为所求. (2分)
(2)如图,△A2B2C2为所求. (5分)
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转90度. (7分)
=×5×2=5. (8分)
17.解:(1)将小路往左平移,直到E,F与A,B重合,则平移后的四边形EFF1E1是一个长方形,并且EF=AB=30,FF1=EE1=1,
则草坪的面积为50×30-1×30=1 470(平方米),
故答案为1 470平方米; (3分)
(2)小路往AB,AD边平移,直到小路与草地的边重合,
则草坪的面积为(50-1)×(30-1)=1 421(平方米); (6分)
(3)将小路往AB,AD,DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为30-1+50+30-1=108(米),
故答案为108米. (10分)
18.解:(1)∵∠ECN=45°,∠ENC=30°,∴∠CEN=105°.
故答案为105°. (1分)
(2)∵OD平分∠MON,∴∠DON=∠MON=×90°=45°,
∴∠DON=∠D=45°,∴CD∥AB,
∴∠CEN=180°-∠MNO=180°-30°=150°. (4分)
(3)如图1,当CD在AB的上方时,设OM与CD相交于点F,
∵CD∥MN,∴∠OFD=∠M=60°,
在△ODF中,∠FOD=180°-∠D-∠OFD=180°-45°-60°=75°,
∴旋转的度数为75°; (7分)
如图2,当CD在AB的下方时,设直线OM与CD相交于点F,
∵CD∥MN,∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转的度数为75°+180°=255°.
综上所述,当边OC旋转75°或255°时,边CD恰好与边MN平行. (12分)
易错警示 这道题涉及图形的平移和旋转.1.对于条件易忽视,三角板的平移,则会带来平行线关系,这个条件易忽视;2.图形在变化,易弄错线段、角之间的对应关系;3.借助画图帮助分析旋转后的图形特点,易画错线段的位置,导致后续的计算错误;4.问题(3)中,只考虑到一种平行情况,实际有两种,思考不全面而容易出错.
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行,如图所示的巴黎奥运会项目图标中,既是轴对称图形又是中心对称图形的是 ( )
2.对折一张长方形的纸,然后用笔尖在上面扎出“B”,再把它打开铺平,你可见到 ( )
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 ( )
A.点A与点A'是对称点 B.BO=B'O
C.∠AOB=∠A'OB' D.∠ACB=∠C'A'B'
4.下列说法正确的是 ( )
A.两个等腰三角形一定全等
B.形状相同的两个三角形全等
C.周长相等的两个三角形全等
D.全等三角形的周长一定相等
5.如图,点P为∠AOB内一点,分别作点P关于直线OA,OB的对称点C,D,若∠COD=70°,则∠CPD的度数是 ( )
A.110° B.135° C.145° D.155°
6.如图,将△OAB绕点O逆时针旋转80°得到△OCD,若∠A=2∠D=100°,则∠α的度数是 ( )
A.60° B.50° C.40° D.30°
7.如图,在△ABC中,∠ACB=90°,∠CAB=38°,以点C为圆心,CB长为半径作弧交AB于点D,分别以D,B为圆心,大于DB长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则∠BCF的度数为 ( )
A.38° B.39° C.40° D.52°
8.如图,两个直角三角形重叠在一起,将△ABC沿点B到点C的方向平移可以得到△DEF,已知AB=12,DH=5,平移的距离为6,则图中阴影部分的面积为 ( )
A.57 B.30 C.42 D.36
二、填空题(本大题共4小题,每小题4分,共16分)
9.如图,该图形绕其中心至少旋转 度就可以与原图形完全重合.
10.如图,这是由六个大小一样的等边三角形拼成的图形,能由标号为1的三角形向右平移而得到的是标号为 的三角形(填写序号即可).
11.如图,△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是 .
12.折纸是一门古老而有趣的艺术,现代数学家藤田文章和羽鸟公士郎甚至为折纸建立了一套完整的“折纸几何学公理”.如图,南南在课余时间拿出一张长方形纸片ABCD(∠A=∠B=∠C=∠D=90°),他先将纸片沿EF折叠,再将折叠后的纸片沿GH折叠,使得GD'与A'B'在同一条直线上,展开纸片后测量发现∠BFE=60°,则∠DGH= °.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,△ABC绕着顶点A逆时针旋转得到△ADE,∠B=40°,∠E=60°,AB∥DE,求∠DAC的度数.
14.(8分)如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE 请说明理由.
15.(8分)图1,图2,图3都是由9个相同的小正方形构成的网格,每个网格图中都有3个小正方形已经涂上了阴影,请在余下的小正方形中,分别按下列要求涂上阴影.
(1)在图1中选取1个涂上阴影,使得4个阴影小正方形组成一个轴对称图形但不是中心对称图形;
(2)在图2中选取1个涂上阴影,使得4个阴影小正方形组成一个中心对称图形但不是轴对称图形;
(3)在图3中选取2个涂上阴影,使得5个阴影小正方形组成一个轴对称图形.
16.(8分)如图,在方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成中心对称图形.
(1)画出此中心对称图形的对称中心O.
(2)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2.
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转 度(不要求证明),并求△CC1C2的面积.
17.(10分)某公园有很多的长方形草地,草地里修了很多有趣的小路,这些草地都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路(FF1=EE1=1),长方形除去阴影部分后剩余部分为草坪,则草坪的面积为 .
(2)如图2,有两条宽均为1米的小路(图中阴影部分),其余部分为草坪,求草坪的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
18.(12分)如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)观察猜想:
将图1中的三角板OCD沿AB的方向平移至图2的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN的度数是 .
(2)操作探究:
将图1中的三角板OCD绕点O按顺时针方向旋转,使边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数.
(3)深化拓展:
将图1中的三角板OCD绕点O按顺时针方向旋转一周,在旋转的过程中,当边OC旋转多少度时,边CD恰好与边MN平行
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C D D C B A A
1.D 解析:A.图形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;B.图形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;C.图形是中心对称图形,但不是轴对称图形,故本选项不符合题意;D.图形既是中心对称图形,也是轴对称图形,故本选项符合题意.
2.C 解析:根据对折之后打开铺平可知,折痕左右的图案是关于折痕成轴对称,观察选项可得只有C选项符合.
3.D 解析:∵△ABC与△A'B'C'关于点O成中心对称,∴点A与点A'是对称点,BO=B'O,∠AOB=∠A'OB',∴A,B,C选项都不符合题意,∵∠ACB与∠C'A'B'不是对应角,∴∠ACB=∠C'A'B'不成立,D选项符合题意.
4.D 解析:A.两个等腰三角形不一定全等,所以此选项不符合题意;B.形状相同的两个三角形不一定全等,所以此选项不符合题意;C.周长相等的两个三角形不一定全等,所以此选项不符合题意;D.全等三角形的周长一定相等,所以此选项符合题意.
5.C 解析:根据对称知,∠C=∠OPC,∠D=∠OPD.∵∠COD=70°,∴∠C+∠D=∠CPD=×(360°-70°)=145°.
6.B 解析:∵将△OAB绕点O逆时针旋转80°,∴∠A=∠C,∠AOC=80°,∴∠DOC=80°-α,∵∠A=2∠D=100°,∴∠D=50°,∴∠C+∠D+∠DOC=180°,∴100°+50°+80°-α=180°,解得α=50°.
7.A 解析:∵∠ACB=90°,∠CAB=38°,∴∠B=90°-∠CAB=52°,由作图可知,CE⊥AB,∴∠BCF=90°-∠B=38°.
8.A 解析:∵将△ABC沿点B到点C的方向平移可以得到△DEF,∴S△ABC=S△DEF,∴S阴影+S△EHC=S梯形ABEH+S△EHC,∴S阴影=S梯形ABEH=×(AB+EH)×BE=×(12+12-5)×6=57.
二、填空题
9.90 解析:把图形中的每个阴影部分与相邻的空白部分当作一个部分,因而整个圆周被分成4个完全相同的部分,每个部分对应的圆心角是360°÷4=90°,因而最少旋转的度数是90°.
10.5 解析:图中标号为5的三角形可由标号为1的三角形向右平移而得到.
11.4 解析:依题意有△DOC的面积等于△AOB的面积,等于6,CD=AB=3,根据三角形的面积公式,得CD边上的高为6×2÷3=4.
12.15 解析:由折叠得,∠AEF=∠A'EF,∠D=∠D'=90°,∠A=∠A'=90°,∠DGH=∠D'GH,∵ABCD是长方形,∠BFE=60°,∴AD∥BC,∴∠AEF+∠BFE=180°,∠GEF=∠BFE=60°,∴∠AEF=120°,∴∠A'EF=120°,∴∠A'EG=∠A'EF-∠GEF=60°,∴∠A'GE=30°,∵GD'与A'B'在同一条直线上,∴∠DGD'=∠A'GE=30°,∴∠DGH=∠DGD'=15°.
三、解答题
13.解:∵△ABC绕着顶点A逆时针旋转得到△ADE,
∴△ABC≌△ADE,
∴∠C=∠E=60°,∠D=∠B=40°,
∴∠BAC=180°-40°-60°=80°,
∵AB∥DE,
∴∠BAD=∠D=40°,
∴∠DAC=∠BAC-∠BAD=80°-40°=40°,
∴∠DAC的度数为40°. (6分)
14.解:(1)证明:∵△BAD≌△ACE,
∴BD=AE,AD=CE.
∴BD=AE=AD+DE=CE+DE,即BD=DE+CE. (4分)
(2)当△ABD满足∠ADB=90°时,BD∥CE. (5分)
理由:当∠ADB=90°时,∠BDE=180°-∠ADB=90°.
∵△BAD≌△ACE,∴∠E=∠ADB=90°,
∴∠BDE=∠E,
∴BD∥CE. (8分)
命题分析 这道题目的关键在于理解全等三角形的性质和平行线的判定方法.问题(1)的证明相对直接,只需要利用全等三角形的性质和线段的和差关系,关键找准对应线段;问题(2)的证明需要更多的几何知识,特别是角度的性质和平行线的判定,这里利用的是内错角相等,两直线平行这个判定.
15.解:(1)如图1所示(答案不唯一); (2分)
(2)如图2所示(答案不唯一); (5分)
(3)如图3所示(答案不唯一). (8分)
16.解:(1)如图,点O为所求. (2分)
(2)如图,△A2B2C2为所求. (5分)
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转90度. (7分)
=×5×2=5. (8分)
17.解:(1)将小路往左平移,直到E,F与A,B重合,则平移后的四边形EFF1E1是一个长方形,并且EF=AB=30,FF1=EE1=1,
则草坪的面积为50×30-1×30=1 470(平方米),
故答案为1 470平方米; (3分)
(2)小路往AB,AD边平移,直到小路与草地的边重合,
则草坪的面积为(50-1)×(30-1)=1 421(平方米); (6分)
(3)将小路往AB,AD,DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为30-1+50+30-1=108(米),
故答案为108米. (10分)
18.解:(1)∵∠ECN=45°,∠ENC=30°,∴∠CEN=105°.
故答案为105°. (1分)
(2)∵OD平分∠MON,∴∠DON=∠MON=×90°=45°,
∴∠DON=∠D=45°,∴CD∥AB,
∴∠CEN=180°-∠MNO=180°-30°=150°. (4分)
(3)如图1,当CD在AB的上方时,设OM与CD相交于点F,
∵CD∥MN,∴∠OFD=∠M=60°,
在△ODF中,∠FOD=180°-∠D-∠OFD=180°-45°-60°=75°,
∴旋转的度数为75°; (7分)
如图2,当CD在AB的下方时,设直线OM与CD相交于点F,
∵CD∥MN,∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转的度数为75°+180°=255°.
综上所述,当边OC旋转75°或255°时,边CD恰好与边MN平行. (12分)
易错警示 这道题涉及图形的平移和旋转.1.对于条件易忽视,三角板的平移,则会带来平行线关系,这个条件易忽视;2.图形在变化,易弄错线段、角之间的对应关系;3.借助画图帮助分析旋转后的图形特点,易画错线段的位置,导致后续的计算错误;4.问题(3)中,只考虑到一种平行情况,实际有两种,思考不全面而容易出错.
