期末测试卷(一)(含答案) 2024-2025学年华东师大版七年级数学下册
文档属性
| 名称 | 期末测试卷(一)(含答案) 2024-2025学年华东师大版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 194.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 10:53:53 | ||
图片预览



文档简介
期末测试卷(一)
时间:90分钟 满分:120分
考试范围:下册全部内容
题序 一 二 三 评卷人 总分
得分
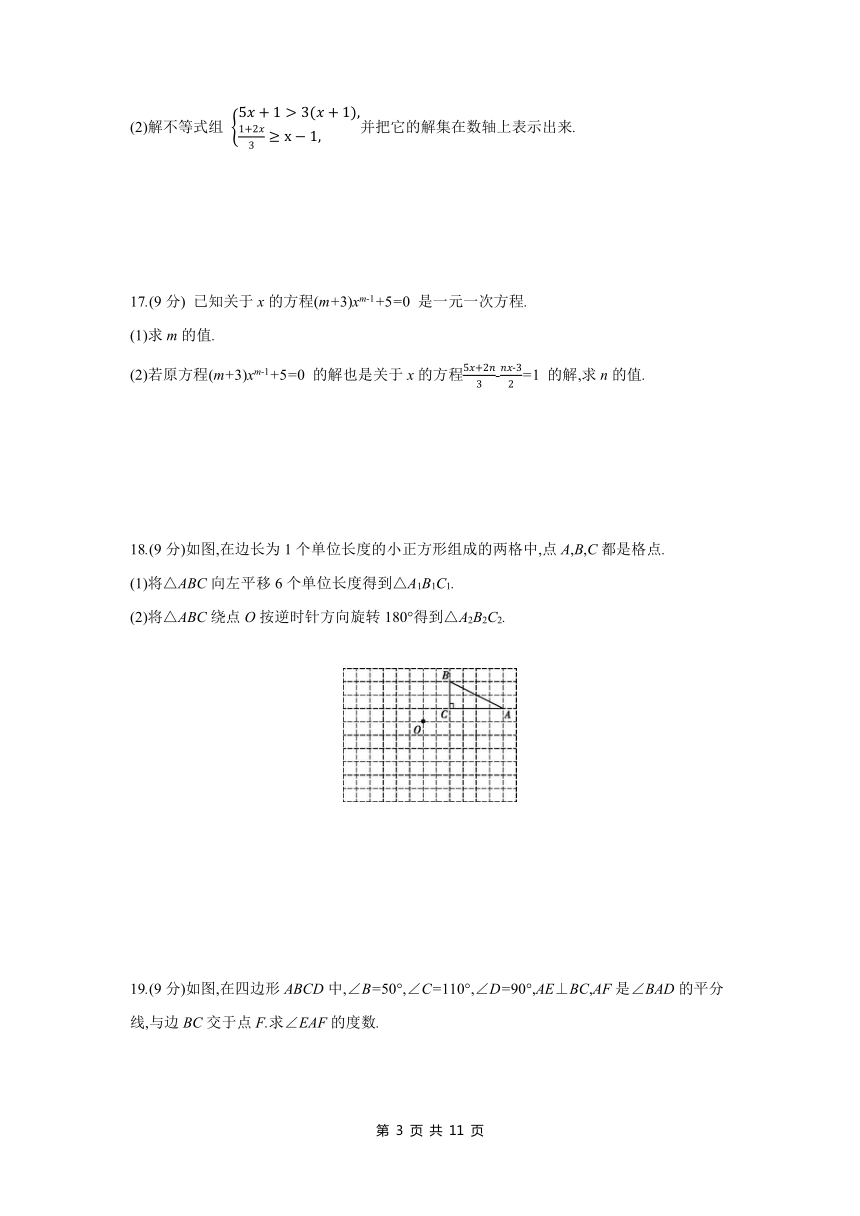
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,下列“月亮”可以由左边图案平移得到的是 ( )
2.二元一次方程2x-y=1有无数多组解,下列四组值中是该方程的解的是 ( )
A. B. C. D.
3.不等式2-x<1的解集在数轴上表示正确的是 ( )
4.下列方程的变形,计算结果正确的同学是 ( )
A.小明 B.小红 C.小英 D.小聪
5.下列图形中,既是轴对称图形又是中心对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
6.《九章算术》中的方程问题:“五只雀、六只燕,共重1斤(等于16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少 ”设每只雀、燕的重量各为x两、y两,可列方程组 ( )
A. B.
C. D.
7.若一个三角形的两个不同的外角之和为300°,那么该三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
8.若不等式组的解集为2A.-1 B.0 C.1 D.2 025
9.△ABC的两边是方程组的解,第三边长为奇数,则符合条件的三角形有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC的度数为 ( )
A.50° B.60° C.70° D.80°
二、填空题(本大题共5小题,每小题3分,共15分)
11.若方程 =3的解是x=5,则a的值为 .
12.某数学学习小组发现:通过连多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有3条,那么该多边形的内角和是 .
13.如图,这个图案是由8个全等的四边形拼成的,其中AD=1 cm,BC=2 cm,则AF= cm.
14.已知则x+y-2 025的值为 .
15.在△ABC中,AH是BC边上的高,若∠BAH=25°,则∠ABC的度数为 .
三、解答题(本大题共8小题,共75分)
16.(10分)(1)解方程组:
(2)解不等式组 并把它的解集在数轴上表示出来.
17.(9分) 已知关于x的方程(m+3)xm-1+5=0 是一元一次方程.
(1)求m的值.
(2)若原方程(m+3)xm-1+5=0 的解也是关于x的方程-=1 的解,求n的值.
18.(9分)如图,在边长为1个单位长度的小正方形组成的两格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1.
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2.
19.(9分)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
20.(9分)如图,这是由五个大小相同的小正方块拼凑而成的.
(1)该图是轴对称图形吗 如果是,请画出对称轴.
(2)若移动一个小方块重新拼凑成一个新的轴对称图形,共有几种方法(相同方法算一种) 请你画出图形和对称轴.
21.(9分)已知a,b,c分别为△ABC的三边长,且满足a+b-4c+24=0,a-b-2c+10=0.
(1)求c的取值范围.
(2)若△ABC的周长为21,求a,b,c的值.
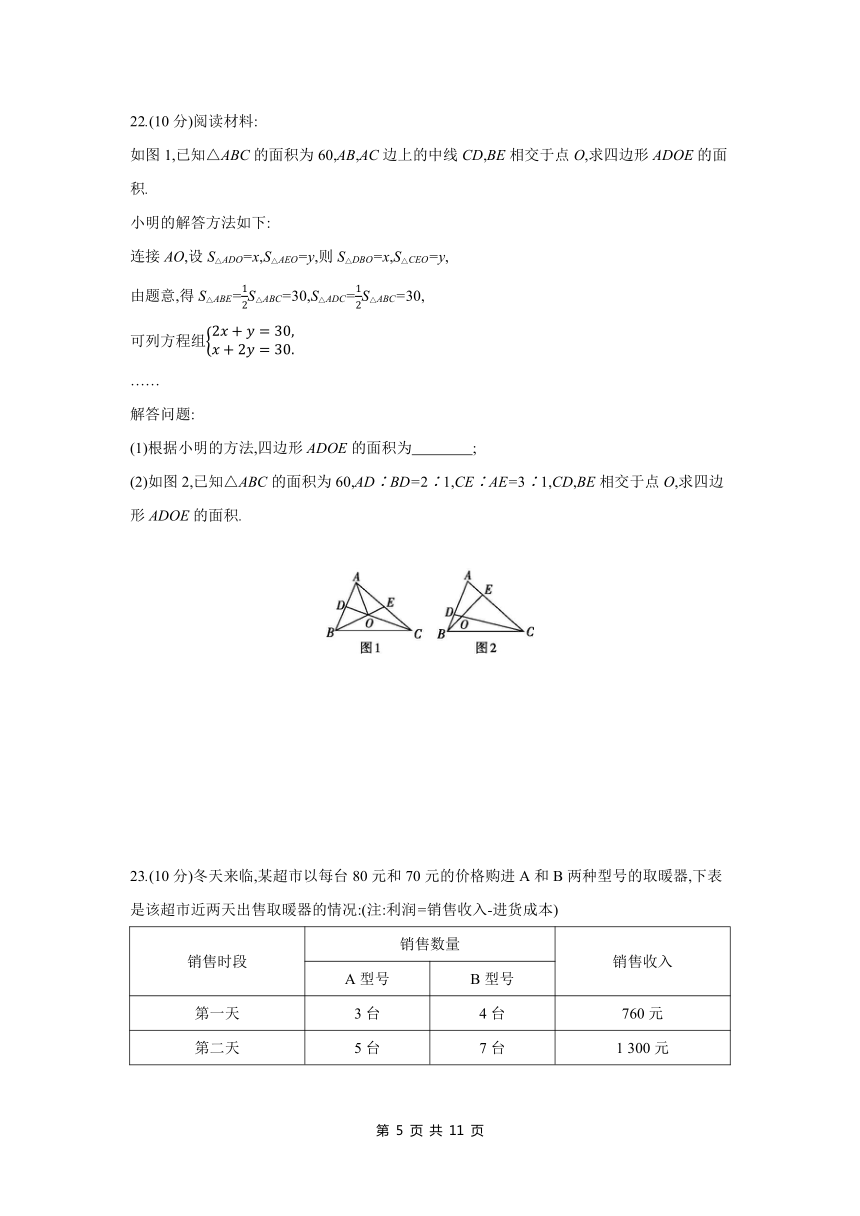
22.(10分)阅读材料:
如图1,已知△ABC的面积为60,AB,AC边上的中线CD,BE相交于点O,求四边形ADOE的面积.
小明的解答方法如下:
连接AO,设S△ADO=x,S△AEO=y,则S△DBO=x,S△CEO=y,
由题意,得S△ABE=S△ABC=30,S△ADC=S△ABC=30,
可列方程组
……
解答问题:
(1)根据小明的方法,四边形ADOE的面积为 ;
(2)如图2,已知△ABC的面积为60,AD∶BD=2∶1,CE∶AE=3∶1,CD,BE相交于点O,求四边形ADOE的面积.
23.(10分)冬天来临,某超市以每台80元和70元的价格购进A和B两种型号的取暖器,下表是该超市近两天出售取暖器的情况:(注:利润=销售收入-进货成本)
销售时段 销售数量 销售收入
A型号 B型号
第一天 3台 4台 760元
第二天 5台 7台 1 300元
(1)分别求A,B两种型号的取暖器的销售单价.
(2)该超市准备用不超过3 020元的资金购进这两种型号的取暖器共40台,则A型号的取暖器最多能采购多少台
(3)在(2)的条件下,超市销售完这40台取暖器能否实现利润超过1 400元的目标 若能,通过计算给出相应的购进方案;若不能,请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C B A D B C C C B C
1.C
2.B 解析:把各选项数值代入方程2x-y=1中,B选项符合.
3.A 解析:不等式2-x<1的解集为x>1,在数轴上表示如A选项所示.
4.D 解析:由2+x=5,得x=5-2;由3x=7,得x=;由3-2(x-2)=-1,得3-2x+4=-1.
5.B 解析:第一个和第三个图形既是轴对称图形又是中心对称图形;第二个图形不是轴对称图形,是中心对称图形;第四个图形是轴对称图形,不是中心对称图形,既是轴对称图形又是中心对称图形的有2个.
6.C
7.C 解析:∵一个三角形的两个不同的外角之和为300°,∴另一个外角为60°,∴这个内角为180°-60°=120°,∴这个三角形是钝角三角形.
8.C 解析:由x-a>0,得x>a,由3x+b<6,得x<,由不等式组的解集为29.B 解析:方程组的解为∵△ABC的两边是方程组的解,第三边长为奇数,∴2<第三边长<6 ,∴第三边长可以为3或5,∴符合条件的三角形有2个.
10.C 解析:∵在△ABC中,∠ACB=90°,∠A=25°,∴∠B=90°-∠A=65°.∵△CBD沿CD折叠得△CED,∴∠BCD= ∠ACB=45°,∴∠BDC=180°-∠B-∠BCD=70°.
二、填空题
11.1 解析:把x=5代入方程 =3,得 =3,解得a=1.
12.720° 解析:∵n边形的一个顶点出发的对角线共有(n-3)条,∴n-3=3,∴n=6,∴内角和=(6-2)×180°=720°.
13.12 解析:由图可知,图中有8个全等的四边形,所以AF=4AD+4BC=4×1+4×2=12 cm.
14.-2 022 解析:①+②,得5x+5y=15,则x+y=3,∴x+y-2 025=3-2 025=-2 022.
15.65°或115° 解析:如图1,∠ABC=90°-25°=65°;如图2,∠ABC=∠AHB+∠BAH=90°+25°=115°.
三、解答题
16.(1)解:由①×4,得2x+8y=28,③
③-②,得y=23,解得y=3.
将y=3代入②,得x=2,
所以原方程组的解为 (5分)
(2)解:
解不等式①,得x>1,
解不等式②,得x≤4.
∴不等式组的解集为1在数轴上表示不等式组的解集如图所示: (10分)
17.解:(1)∵关于x的方程(m+3)xm-1+5=0 是一元一次方程,
∴m-1=1,解得m=2.
(2)把m=2代入原方程,得5x+5=0,解得x=-1. (4分)
把x=-1代入方程-=1 ,得-=1 ,
去分母,得2(-5+2n)-3(-n-3)=6,
去括号,得-10+4n+3n+9=6,
移项、合并同类项,得7n=7,
解得n=1. (9分)
18.解:(1)如图,△A1B1C1为所求. (4分)
(2)如图,△A2B2C2为所求. (9分)
19.解:∵∠B=50°,∠C=110°,∠D=90°,
∴∠BAD=360°-∠B-∠C-∠D=110°.
∵AF是∠BAD的平分线,
∴∠BAF=∠BAD=55°. (5分)
∵AE⊥BC,∴∠AEB=90°,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAF=∠BAF-∠BAE=55°-40°=15°. (9分)
20.解:(1)是轴对称图形,对称轴如图所示. (2分)
(2)有3种,如图. (9分)
21.解:(1)根据三角形三边关系可知a+b>c,a-b∵a+b-4c+24=0,a-b-2c+10=0,∴a+b=4c-24,a-b=2c-10,
∴解得8(2)根据题意,得解得
∴3c-17+c-7+c=21,解得c=9,
∴a=3×9-17=10,b=9-7=2. (9分)
22.解:(1)连接AO,设S△ADO=x,S△AEO=y,则S△DBO=x,S△CEO=y,
由题意,得S△ABE=S△ABC=30,S△ADC=S△ABC=30,
可列方程组
解得
∴S四边形ADOE=S△ADO+S△AEO=x+y=20,
故答案为20. (3分)
(2)连接AO,如图所示:
设S△DBO=a,S△AEO=b,
∵AD∶BD=2∶1,CE∶AE=3∶1,
∴S△ADO=2a,S△CEO=3b,
∴S△ACD=2a+4b,S△ABE=3a+b,S四边形ADOE=2a+b,
∵AD∶BD=2∶1,CE∶AE=3∶1,
∴AD∶AB=2∶3,AE∶AC=1∶4,
∴S△ACD=S△ABC=40,S△ABE=S△ABC=15,
∴
解得
∴S四边形ADOE=2a+b=13. (10分)
核心突破 此题主要考查了三角形的面积,由三角形的中线与面积的关系推广到一般比例情况,并利用了方程思想求解,解答此题的关键是理解同高(或等高)的两个三角形的面积之比等于对应底边的比.
23.解:(1)设A,B两种型号取暖器的销售单价分别为x元、y元.
根据题意,得解得
答:A,B两种型号取暖器的销售单价分别为120元、100元. (3分)
(2)设购进A型号取暖器a台,则购进B型号取暖器(40-a)台.
根据题意,得80a+70(40-a)≤3 020,解得a≤22.
答:A型号的取暖器最多能采购22台. (6分)
(3)由(2)可得(120-80)a+(100-70)(40-a)>1 400,解得a>20.
因为a≤22且a为整数,
所以a可取21或22,
所以在(2)的条件下该超市能实现利润超过1 400元的目标.
购进方案:
方案一:购进A型号取暖器21台,B型号取暖器19台.
方案二:购进A型号取暖器22台,B型号取暖器18台. (10分)
时间:90分钟 满分:120分
考试范围:下册全部内容
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,下列“月亮”可以由左边图案平移得到的是 ( )
2.二元一次方程2x-y=1有无数多组解,下列四组值中是该方程的解的是 ( )
A. B. C. D.
3.不等式2-x<1的解集在数轴上表示正确的是 ( )
4.下列方程的变形,计算结果正确的同学是 ( )
A.小明 B.小红 C.小英 D.小聪
5.下列图形中,既是轴对称图形又是中心对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
6.《九章算术》中的方程问题:“五只雀、六只燕,共重1斤(等于16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少 ”设每只雀、燕的重量各为x两、y两,可列方程组 ( )
A. B.
C. D.
7.若一个三角形的两个不同的外角之和为300°,那么该三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
8.若不等式组的解集为2
9.△ABC的两边是方程组的解,第三边长为奇数,则符合条件的三角形有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC的度数为 ( )
A.50° B.60° C.70° D.80°
二、填空题(本大题共5小题,每小题3分,共15分)
11.若方程 =3的解是x=5,则a的值为 .
12.某数学学习小组发现:通过连多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有3条,那么该多边形的内角和是 .
13.如图,这个图案是由8个全等的四边形拼成的,其中AD=1 cm,BC=2 cm,则AF= cm.
14.已知则x+y-2 025的值为 .
15.在△ABC中,AH是BC边上的高,若∠BAH=25°,则∠ABC的度数为 .
三、解答题(本大题共8小题,共75分)
16.(10分)(1)解方程组:
(2)解不等式组 并把它的解集在数轴上表示出来.
17.(9分) 已知关于x的方程(m+3)xm-1+5=0 是一元一次方程.
(1)求m的值.
(2)若原方程(m+3)xm-1+5=0 的解也是关于x的方程-=1 的解,求n的值.
18.(9分)如图,在边长为1个单位长度的小正方形组成的两格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1.
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2.
19.(9分)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
20.(9分)如图,这是由五个大小相同的小正方块拼凑而成的.
(1)该图是轴对称图形吗 如果是,请画出对称轴.
(2)若移动一个小方块重新拼凑成一个新的轴对称图形,共有几种方法(相同方法算一种) 请你画出图形和对称轴.
21.(9分)已知a,b,c分别为△ABC的三边长,且满足a+b-4c+24=0,a-b-2c+10=0.
(1)求c的取值范围.
(2)若△ABC的周长为21,求a,b,c的值.
22.(10分)阅读材料:
如图1,已知△ABC的面积为60,AB,AC边上的中线CD,BE相交于点O,求四边形ADOE的面积.
小明的解答方法如下:
连接AO,设S△ADO=x,S△AEO=y,则S△DBO=x,S△CEO=y,
由题意,得S△ABE=S△ABC=30,S△ADC=S△ABC=30,
可列方程组
……
解答问题:
(1)根据小明的方法,四边形ADOE的面积为 ;
(2)如图2,已知△ABC的面积为60,AD∶BD=2∶1,CE∶AE=3∶1,CD,BE相交于点O,求四边形ADOE的面积.
23.(10分)冬天来临,某超市以每台80元和70元的价格购进A和B两种型号的取暖器,下表是该超市近两天出售取暖器的情况:(注:利润=销售收入-进货成本)
销售时段 销售数量 销售收入
A型号 B型号
第一天 3台 4台 760元
第二天 5台 7台 1 300元
(1)分别求A,B两种型号的取暖器的销售单价.
(2)该超市准备用不超过3 020元的资金购进这两种型号的取暖器共40台,则A型号的取暖器最多能采购多少台
(3)在(2)的条件下,超市销售完这40台取暖器能否实现利润超过1 400元的目标 若能,通过计算给出相应的购进方案;若不能,请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C B A D B C C C B C
1.C
2.B 解析:把各选项数值代入方程2x-y=1中,B选项符合.
3.A 解析:不等式2-x<1的解集为x>1,在数轴上表示如A选项所示.
4.D 解析:由2+x=5,得x=5-2;由3x=7,得x=;由3-2(x-2)=-1,得3-2x+4=-1.
5.B 解析:第一个和第三个图形既是轴对称图形又是中心对称图形;第二个图形不是轴对称图形,是中心对称图形;第四个图形是轴对称图形,不是中心对称图形,既是轴对称图形又是中心对称图形的有2个.
6.C
7.C 解析:∵一个三角形的两个不同的外角之和为300°,∴另一个外角为60°,∴这个内角为180°-60°=120°,∴这个三角形是钝角三角形.
8.C 解析:由x-a>0,得x>a,由3x+b<6,得x<,由不等式组的解集为2
10.C 解析:∵在△ABC中,∠ACB=90°,∠A=25°,∴∠B=90°-∠A=65°.∵△CBD沿CD折叠得△CED,∴∠BCD= ∠ACB=45°,∴∠BDC=180°-∠B-∠BCD=70°.
二、填空题
11.1 解析:把x=5代入方程 =3,得 =3,解得a=1.
12.720° 解析:∵n边形的一个顶点出发的对角线共有(n-3)条,∴n-3=3,∴n=6,∴内角和=(6-2)×180°=720°.
13.12 解析:由图可知,图中有8个全等的四边形,所以AF=4AD+4BC=4×1+4×2=12 cm.
14.-2 022 解析:①+②,得5x+5y=15,则x+y=3,∴x+y-2 025=3-2 025=-2 022.
15.65°或115° 解析:如图1,∠ABC=90°-25°=65°;如图2,∠ABC=∠AHB+∠BAH=90°+25°=115°.
三、解答题
16.(1)解:由①×4,得2x+8y=28,③
③-②,得y=23,解得y=3.
将y=3代入②,得x=2,
所以原方程组的解为 (5分)
(2)解:
解不等式①,得x>1,
解不等式②,得x≤4.
∴不等式组的解集为1
17.解:(1)∵关于x的方程(m+3)xm-1+5=0 是一元一次方程,
∴m-1=1,解得m=2.
(2)把m=2代入原方程,得5x+5=0,解得x=-1. (4分)
把x=-1代入方程-=1 ,得-=1 ,
去分母,得2(-5+2n)-3(-n-3)=6,
去括号,得-10+4n+3n+9=6,
移项、合并同类项,得7n=7,
解得n=1. (9分)
18.解:(1)如图,△A1B1C1为所求. (4分)
(2)如图,△A2B2C2为所求. (9分)
19.解:∵∠B=50°,∠C=110°,∠D=90°,
∴∠BAD=360°-∠B-∠C-∠D=110°.
∵AF是∠BAD的平分线,
∴∠BAF=∠BAD=55°. (5分)
∵AE⊥BC,∴∠AEB=90°,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAF=∠BAF-∠BAE=55°-40°=15°. (9分)
20.解:(1)是轴对称图形,对称轴如图所示. (2分)
(2)有3种,如图. (9分)
21.解:(1)根据三角形三边关系可知a+b>c,a-b
∴解得8
∴3c-17+c-7+c=21,解得c=9,
∴a=3×9-17=10,b=9-7=2. (9分)
22.解:(1)连接AO,设S△ADO=x,S△AEO=y,则S△DBO=x,S△CEO=y,
由题意,得S△ABE=S△ABC=30,S△ADC=S△ABC=30,
可列方程组
解得
∴S四边形ADOE=S△ADO+S△AEO=x+y=20,
故答案为20. (3分)
(2)连接AO,如图所示:
设S△DBO=a,S△AEO=b,
∵AD∶BD=2∶1,CE∶AE=3∶1,
∴S△ADO=2a,S△CEO=3b,
∴S△ACD=2a+4b,S△ABE=3a+b,S四边形ADOE=2a+b,
∵AD∶BD=2∶1,CE∶AE=3∶1,
∴AD∶AB=2∶3,AE∶AC=1∶4,
∴S△ACD=S△ABC=40,S△ABE=S△ABC=15,
∴
解得
∴S四边形ADOE=2a+b=13. (10分)
核心突破 此题主要考查了三角形的面积,由三角形的中线与面积的关系推广到一般比例情况,并利用了方程思想求解,解答此题的关键是理解同高(或等高)的两个三角形的面积之比等于对应底边的比.
23.解:(1)设A,B两种型号取暖器的销售单价分别为x元、y元.
根据题意,得解得
答:A,B两种型号取暖器的销售单价分别为120元、100元. (3分)
(2)设购进A型号取暖器a台,则购进B型号取暖器(40-a)台.
根据题意,得80a+70(40-a)≤3 020,解得a≤22.
答:A型号的取暖器最多能采购22台. (6分)
(3)由(2)可得(120-80)a+(100-70)(40-a)>1 400,解得a>20.
因为a≤22且a为整数,
所以a可取21或22,
所以在(2)的条件下该超市能实现利润超过1 400元的目标.
购进方案:
方案一:购进A型号取暖器21台,B型号取暖器19台.
方案二:购进A型号取暖器22台,B型号取暖器18台. (10分)
同课章节目录
