2.2 一元二次方程的应用 学案(无答案)北师大版数学九年级上册
文档属性
| 名称 | 2.2 一元二次方程的应用 学案(无答案)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 499.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 00:00:00 | ||
图片预览



文档简介
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.07.14
第二章 一元二次方程
§2.2 一元二次方程的应用
【学习目标】
1. 在已有的一元二次方程解法的基础上,探索出一元二次方程根与系数的关系并运用;
2. 经历用一元二次方程解会用一元二次方程解决有关几何问题,进一步理解方程是刻画客观世界的有效模型;
3. 能够熟练列一元二次方程的方法解决有关商品的销售问题和平均变化率等问题。
【学习过程】
一、一元二次方程的根与系数的关系
一元二次方程根与系数的关系(韦达定理):=__________,=__________。
例1 已知方程的一个根是2,求它的另一个根及k的值。
例2 设是方程的两个根,不解方程,求代数式和的值。
[识记理解1]
1. 设是一元二次方程的两个根,不解方程,求代数式和的值。
2. 已知方程的一个根是1,求它的另一个根及m的值。
3. 求一个一元二次方程,使它的两个根分别为(1)4,;(2),。
二、几何问题
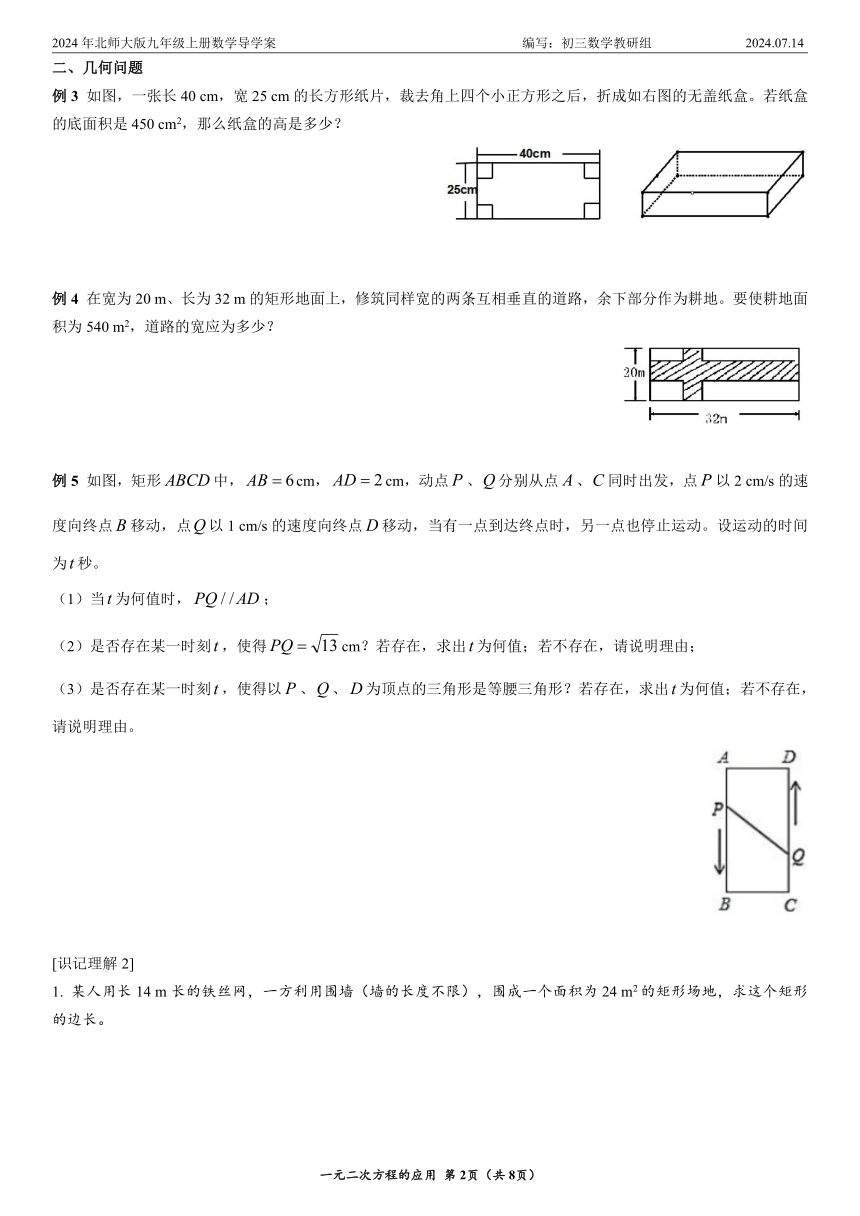
例3 如图,一张长40 cm,宽25 cm的长方形纸片,裁去角上四个小正方形之后,折成如右图的无盖纸盒。若纸盒的底面积是450 cm2,那么纸盒的高是多少?
例4 在宽为20 m、长为32 m的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为耕地。要使耕地面积为540 m2,道路的宽应为多少?
例5 如图,矩形中,cm,cm,动点、分别从点、同时出发,点以2 cm/s的速度向终点移动,点以1 cm/s的速度向终点移动,当有一点到达终点时,另一点也停止运动。设运动的时间为秒。
(1)当为何值时,;
(2)是否存在某一时刻,使得cm?若存在,求出为何值;若不存在,请说明理由;
(3)是否存在某一时刻,使得以、、为顶点的三角形是等腰三角形?若存在,求出为何值;若不存在,请说明理由。
[识记理解2]
1. 某人用长14 m长的铁丝网,一方利用围墙(墙的长度不限),围成一个面积为24 m2的矩形场地,求这个矩形的边长。
2. 在长为40米、宽为22米的矩形地面内,修筑两条同样宽且互相垂直的道路,余下的铺上草坪,要使草坪的面积达到760平方米,道路的宽应为多少?
三、变化率问题
例6 为了绿化学校附近的荒山,某校初三年级学生连续三年春季上山植树,至今已成活了2000棵。已知这些学生在初一时种了400棵,若平均成活率95%,求这个年级每年植树数的平均增长率。(精确到0.1%)
例7 在某次举行的促销活动中,某商品经连续两次降价后,售价变为原来的81%,若两次降价的百分率相同,求该商品每次降价的百分率。
[识记理解3]
1. 某服装店花1200元进了一批服装,按40%的利润定价,无人购买,决定打折出售。但仍无人购买,结果又一次打折后才售完,经结算这批服装共盈利280元。若两次打折相同,问每次打了多少折?
2. 近期,哈尔滨冰雪大世界受到广大游客的喜爱,游玩人数剧增,元旦三天假期,第一天游客数量a万人,第二天人数比第一天增长200%,第三天在第二天的基础上回落25%,求第二天和第三天这两天的平均增长率。
四、营销经济问题
例8 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施。经调查发现,在一定范围内,衬衫的单价每降一元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1200元,衬衫的单价应降多少元?
例9 新华商场销售某种冰箱,每台进价为2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台。商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
[识记理解4]
1. 某商场礼品柜台购进大量贺年卡,一种贺年卡平均每天可销售500张,每张盈利0.3元。为了尽快减少库存,商场决定采取适当的措施。调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天多售出300张。商场要想平均每天盈利160元,每张贺年卡应降价多少元?
2. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个。调查表明:这种台灯的售价每上涨1元,其销售量就将减少10个。为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
3. 一个农业合作社以64000元的成本收获了某种农产品80 t,目前可以以1200元/t的价格售出。如果储藏起来,每星期会损失2 t,且每星期需支付各种费用1600元,但同时每星期每吨的价格将上涨200元。那么,储藏多少个星期出售这批农产品可获利122000元?
【知能提升】
一、选择题
1. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )
A. . B. C. D.
2. 鸡瘟是一种传播速度很快的传染病,一轮传染为一天的时间,某养鸡场于某日发现一例鸡瘟病例,两天后发现共有169只鸡患有这种病。若每例病鸡传染健康鸡的只数均相同,则每只病鸡传染健康鸡的只数为( )
A. 11只 B. 12只. C. 13只 D. 14只
3. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理)。销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件。已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )
A. B.
C. D. .
4. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )
A. B. C. . D.
5. 《周髀算经》中有一种几何方法可以用来解形如的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为:24×4+25=121,边长为11,故得的正数解为,小明按此方法解关于x的方程时,构造出同样的图形。已知大正方形的面积为10,小正方形的面积为4,则( )
A. , B. , C. , D. ,.
6. 2023年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包。若此次抢红包活动,群内所有人共收到90个红包,则该群一共有( )
A. 9人 B. 10人. C. 11人 D. 12人
7. 某商店从厂家以每件18元的价格购进一批商品。该商品可以自行定价。据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出件,但物价部门限定每件商品加价不能超过进货价的25%,如果商店计划要获利400元。则每件商品的售价应定为( )
A. 22元. B. 24元 C. 26元 D. 28元
8. 如图1,在矩形中,动点从点出发,以2 cm/s的速度沿折线向终点运动。设点的运动时间为t s,△的面积为S cm2,图2是点运动过程中S与t之间函数关系的图象,则的长为( )
A. 10 cm. B. 8 cm C. 14 cm D. 12 cm
二、填空题
9. 已知,是方程的两个根,则的值是______________。
10. 有一人患了流感,经过两轮传染后共有169人患了流感,每轮传染中平均一个人传染了_______人。
11. 如图,小明同学用一张长11 cm,宽7 cm的矩形纸板制作一个底面积为21 cm2的无盖长方体纸盒。他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计)。设剪去的正方形边长为x cm,则可列出关于x的方程为______________________________。
第11题图 第12题图
12. 如图,有一块长20 cm,宽10 cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96 cm2的无盖的盒子,则这个盒子的容积为____________cm3。
13. 将进货单价为40元的商品按50元出售时,就能卖出500个,已知这种商品每个涨价1元,其销售量就减少10个,为了赚得8000元的利润,商品售价应为________元。
14. 2021年7月29日,山西省政府新闻办举行新闻发布会,2020年山西省教育经费支出首次突破700亿元,达到733.4亿元,成为继社会保障支出后的第二大支出。据有关资料显示,2018年山西省教育经费支出为668.96亿元,若2019,2020这两年山西省教育经费支出的年平均增长率相同,求这两年的年平均增长率。若设这两年的年平均增长率为x,则根据题意,可列方程为______________________________。
15. 如图,在等腰中,,cm,动点从点出发沿折线向点终以cm/s的速度运动,于点。设运动时间为t s,当t =___________s时,△的面积为4 cm2。
第15题图 第16题图
16. 某农场要建一个饲养场(矩形),两面靠现有墙(位置的墙最大可用长度为27 m,位置的墙最大可用长度为15 m),另两面用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图的三处各留1 m宽的门(不用木栏)。建成后木栏总长45 m。若饲养场的面积为180 m2,则饲养场的一边的长为_______。
三、解答题
17. 已知关于x的方程。
(1)证明:此方程有两个不相等的实数根。
(2)设此方程的两个根分别为,,若,求m的值。
18. 受益于国家支持新能源汽车发展和“一带一路”发展战略,某市汽车零部件生产企业的利润逐年提高,据统计,2022年利润为2亿元,2024年利润为2.88亿元。
(1)求该企业从2022年到2024年利润的年平均增长率;
(2)若利润的年平均增长率不变,该企业2025年的利润能否超过3.5亿元?
19. 如图,某中学课外兴题小组准备围建一个矩形花园,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边上要预留2 m宽的入口(如图中所示,不用篱笆),已知墙长为28 m。
(1)当矩形的长为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园?若能,求出长;若不能,说明理由。
20. 在刚刚过去的“五一”假期中,某超市为迎接“五一”小长假购物高潮,经销甲、乙两种品牌的洗衣液。市场上甲种品牌洗衣液的进价比乙种品牌洗衣液的进价每瓶便宜10元,该超市用6000元购进的甲种品牌洗衣液与用8000元购进的乙种品牌洗衣液的瓶数相同。
(1)求甲、乙两种品牌的洗衣液的进价;
(2)在销售中,该超市决定将甲种品牌的洗衣液以每瓶45元售出,每天固定售出100瓶;但调查发现,乙种品牌的洗衣液每瓶售价50元时,每天可售出140瓶,并且当乙种品牌的洗衣液每瓶售价每提高1元时,乙种品牌的洗衣液每天就会少售出2瓶,当乙种品牌的洗衣液的每瓶售价为多少元时,两种品牌的洗衣液每天的利润之和可达到4700元?
21. 如图,在中,,cm,cm,点从点开始沿边向点以1 cm/s的速度移动,点从点开始沿边向点以2 cm/s的速度移动,点与点分别从点、点同时出发,当有一点到达终点时,另一点也停止运动。设运动的时间为秒。
(1)求同时出发几秒后,cm;
(2)的面积能否等于7 cm2,若能,请求出此时运动的时间;若不能,请说明理由。
一元二次方程的应用 第1页(共7页)
第二章 一元二次方程
§2.2 一元二次方程的应用
【学习目标】
1. 在已有的一元二次方程解法的基础上,探索出一元二次方程根与系数的关系并运用;
2. 经历用一元二次方程解会用一元二次方程解决有关几何问题,进一步理解方程是刻画客观世界的有效模型;
3. 能够熟练列一元二次方程的方法解决有关商品的销售问题和平均变化率等问题。
【学习过程】
一、一元二次方程的根与系数的关系
一元二次方程根与系数的关系(韦达定理):=__________,=__________。
例1 已知方程的一个根是2,求它的另一个根及k的值。
例2 设是方程的两个根,不解方程,求代数式和的值。
[识记理解1]
1. 设是一元二次方程的两个根,不解方程,求代数式和的值。
2. 已知方程的一个根是1,求它的另一个根及m的值。
3. 求一个一元二次方程,使它的两个根分别为(1)4,;(2),。
二、几何问题
例3 如图,一张长40 cm,宽25 cm的长方形纸片,裁去角上四个小正方形之后,折成如右图的无盖纸盒。若纸盒的底面积是450 cm2,那么纸盒的高是多少?
例4 在宽为20 m、长为32 m的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为耕地。要使耕地面积为540 m2,道路的宽应为多少?
例5 如图,矩形中,cm,cm,动点、分别从点、同时出发,点以2 cm/s的速度向终点移动,点以1 cm/s的速度向终点移动,当有一点到达终点时,另一点也停止运动。设运动的时间为秒。
(1)当为何值时,;
(2)是否存在某一时刻,使得cm?若存在,求出为何值;若不存在,请说明理由;
(3)是否存在某一时刻,使得以、、为顶点的三角形是等腰三角形?若存在,求出为何值;若不存在,请说明理由。
[识记理解2]
1. 某人用长14 m长的铁丝网,一方利用围墙(墙的长度不限),围成一个面积为24 m2的矩形场地,求这个矩形的边长。
2. 在长为40米、宽为22米的矩形地面内,修筑两条同样宽且互相垂直的道路,余下的铺上草坪,要使草坪的面积达到760平方米,道路的宽应为多少?
三、变化率问题
例6 为了绿化学校附近的荒山,某校初三年级学生连续三年春季上山植树,至今已成活了2000棵。已知这些学生在初一时种了400棵,若平均成活率95%,求这个年级每年植树数的平均增长率。(精确到0.1%)
例7 在某次举行的促销活动中,某商品经连续两次降价后,售价变为原来的81%,若两次降价的百分率相同,求该商品每次降价的百分率。
[识记理解3]
1. 某服装店花1200元进了一批服装,按40%的利润定价,无人购买,决定打折出售。但仍无人购买,结果又一次打折后才售完,经结算这批服装共盈利280元。若两次打折相同,问每次打了多少折?
2. 近期,哈尔滨冰雪大世界受到广大游客的喜爱,游玩人数剧增,元旦三天假期,第一天游客数量a万人,第二天人数比第一天增长200%,第三天在第二天的基础上回落25%,求第二天和第三天这两天的平均增长率。
四、营销经济问题
例8 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施。经调查发现,在一定范围内,衬衫的单价每降一元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1200元,衬衫的单价应降多少元?
例9 新华商场销售某种冰箱,每台进价为2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台。商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
[识记理解4]
1. 某商场礼品柜台购进大量贺年卡,一种贺年卡平均每天可销售500张,每张盈利0.3元。为了尽快减少库存,商场决定采取适当的措施。调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天多售出300张。商场要想平均每天盈利160元,每张贺年卡应降价多少元?
2. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个。调查表明:这种台灯的售价每上涨1元,其销售量就将减少10个。为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
3. 一个农业合作社以64000元的成本收获了某种农产品80 t,目前可以以1200元/t的价格售出。如果储藏起来,每星期会损失2 t,且每星期需支付各种费用1600元,但同时每星期每吨的价格将上涨200元。那么,储藏多少个星期出售这批农产品可获利122000元?
【知能提升】
一、选择题
1. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )
A. . B. C. D.
2. 鸡瘟是一种传播速度很快的传染病,一轮传染为一天的时间,某养鸡场于某日发现一例鸡瘟病例,两天后发现共有169只鸡患有这种病。若每例病鸡传染健康鸡的只数均相同,则每只病鸡传染健康鸡的只数为( )
A. 11只 B. 12只. C. 13只 D. 14只
3. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理)。销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件。已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )
A. B.
C. D. .
4. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )
A. B. C. . D.
5. 《周髀算经》中有一种几何方法可以用来解形如的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为:24×4+25=121,边长为11,故得的正数解为,小明按此方法解关于x的方程时,构造出同样的图形。已知大正方形的面积为10,小正方形的面积为4,则( )
A. , B. , C. , D. ,.
6. 2023年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包。若此次抢红包活动,群内所有人共收到90个红包,则该群一共有( )
A. 9人 B. 10人. C. 11人 D. 12人
7. 某商店从厂家以每件18元的价格购进一批商品。该商品可以自行定价。据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出件,但物价部门限定每件商品加价不能超过进货价的25%,如果商店计划要获利400元。则每件商品的售价应定为( )
A. 22元. B. 24元 C. 26元 D. 28元
8. 如图1,在矩形中,动点从点出发,以2 cm/s的速度沿折线向终点运动。设点的运动时间为t s,△的面积为S cm2,图2是点运动过程中S与t之间函数关系的图象,则的长为( )
A. 10 cm. B. 8 cm C. 14 cm D. 12 cm
二、填空题
9. 已知,是方程的两个根,则的值是______________。
10. 有一人患了流感,经过两轮传染后共有169人患了流感,每轮传染中平均一个人传染了_______人。
11. 如图,小明同学用一张长11 cm,宽7 cm的矩形纸板制作一个底面积为21 cm2的无盖长方体纸盒。他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计)。设剪去的正方形边长为x cm,则可列出关于x的方程为______________________________。
第11题图 第12题图
12. 如图,有一块长20 cm,宽10 cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96 cm2的无盖的盒子,则这个盒子的容积为____________cm3。
13. 将进货单价为40元的商品按50元出售时,就能卖出500个,已知这种商品每个涨价1元,其销售量就减少10个,为了赚得8000元的利润,商品售价应为________元。
14. 2021年7月29日,山西省政府新闻办举行新闻发布会,2020年山西省教育经费支出首次突破700亿元,达到733.4亿元,成为继社会保障支出后的第二大支出。据有关资料显示,2018年山西省教育经费支出为668.96亿元,若2019,2020这两年山西省教育经费支出的年平均增长率相同,求这两年的年平均增长率。若设这两年的年平均增长率为x,则根据题意,可列方程为______________________________。
15. 如图,在等腰中,,cm,动点从点出发沿折线向点终以cm/s的速度运动,于点。设运动时间为t s,当t =___________s时,△的面积为4 cm2。
第15题图 第16题图
16. 某农场要建一个饲养场(矩形),两面靠现有墙(位置的墙最大可用长度为27 m,位置的墙最大可用长度为15 m),另两面用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图的三处各留1 m宽的门(不用木栏)。建成后木栏总长45 m。若饲养场的面积为180 m2,则饲养场的一边的长为_______。
三、解答题
17. 已知关于x的方程。
(1)证明:此方程有两个不相等的实数根。
(2)设此方程的两个根分别为,,若,求m的值。
18. 受益于国家支持新能源汽车发展和“一带一路”发展战略,某市汽车零部件生产企业的利润逐年提高,据统计,2022年利润为2亿元,2024年利润为2.88亿元。
(1)求该企业从2022年到2024年利润的年平均增长率;
(2)若利润的年平均增长率不变,该企业2025年的利润能否超过3.5亿元?
19. 如图,某中学课外兴题小组准备围建一个矩形花园,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边上要预留2 m宽的入口(如图中所示,不用篱笆),已知墙长为28 m。
(1)当矩形的长为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园?若能,求出长;若不能,说明理由。
20. 在刚刚过去的“五一”假期中,某超市为迎接“五一”小长假购物高潮,经销甲、乙两种品牌的洗衣液。市场上甲种品牌洗衣液的进价比乙种品牌洗衣液的进价每瓶便宜10元,该超市用6000元购进的甲种品牌洗衣液与用8000元购进的乙种品牌洗衣液的瓶数相同。
(1)求甲、乙两种品牌的洗衣液的进价;
(2)在销售中,该超市决定将甲种品牌的洗衣液以每瓶45元售出,每天固定售出100瓶;但调查发现,乙种品牌的洗衣液每瓶售价50元时,每天可售出140瓶,并且当乙种品牌的洗衣液每瓶售价每提高1元时,乙种品牌的洗衣液每天就会少售出2瓶,当乙种品牌的洗衣液的每瓶售价为多少元时,两种品牌的洗衣液每天的利润之和可达到4700元?
21. 如图,在中,,cm,cm,点从点开始沿边向点以1 cm/s的速度移动,点从点开始沿边向点以2 cm/s的速度移动,点与点分别从点、点同时出发,当有一点到达终点时,另一点也停止运动。设运动的时间为秒。
(1)求同时出发几秒后,cm;
(2)的面积能否等于7 cm2,若能,请求出此时运动的时间;若不能,请说明理由。
一元二次方程的应用 第1页(共7页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
