4.2 相似多边形与相似三角形的判定定理 导学案(无答案)北师大版九年级上册数学
文档属性
| 名称 | 4.2 相似多边形与相似三角形的判定定理 导学案(无答案)北师大版九年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 922.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:25:35 | ||
图片预览

文档简介
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.10.19
第四章 图形的相似
§4.2 相似多边形与相似三角形的判定定理
【学习目标】
1. 掌握相似三角形和相似多边形的概念,并灵活运用相似三角形的判定定理证明和解决有关问题;
2. 掌握黄金分割的基本概念,提高运用“类比”思想的自觉性,提高推理能力。
【学习过程】
一、相似多边形的定义、判定与性质
1. 定义:各角分别______________,各边_____________的两个多边形叫做相似多边形。相似多边形的对应边的比叫做_____________,通常用_____来表示。
2. 性质:相似多边形的对应角___________,对应边_____________。
3. 判定:如果两个多边形的对应角___________,对应边的比___________,那么这两个多边形相似。
例1 如图,矩形的长,宽。
(1)如图①,若沿矩形四周有宽为2的环形区域,图中所形成的两个矩形与相似吗?请说明理由。
(2)如图②,为多少时,图中的两个矩形相似?
[识记理解1]
1. 将一张报纸对折后的半张报纸和整张报纸相似,则整张报纸的宽与长的比为多少?
二、相似三角形的判定定理
1. 判定定理1:_____________________________________________________________________________。
例2 如图,和的边、相交于点,且,点在上,求证:。
[识记理解2]
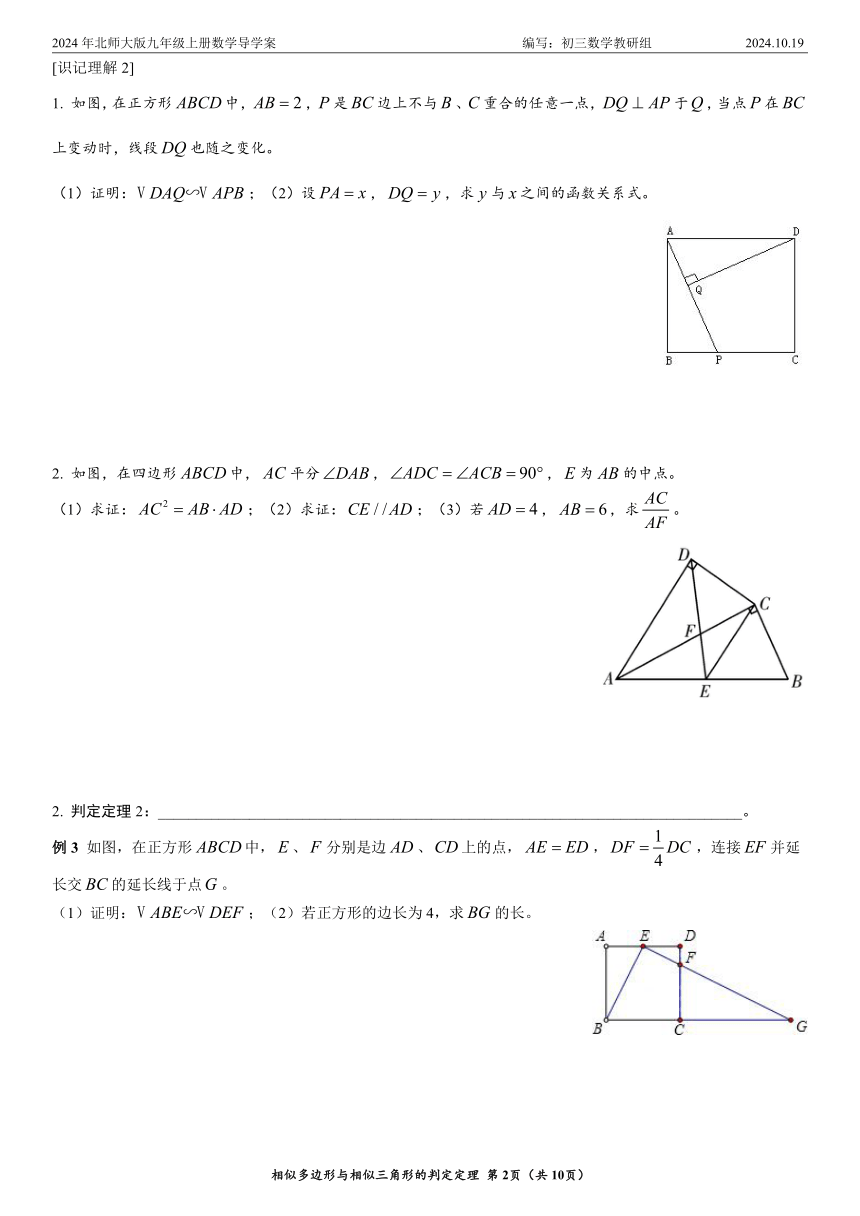
1. 如图,在正方形中,,是边上不与、重合的任意一点,于,当点在上变动时,线段也随之变化。
(1)证明:;(2)设,,求与之间的函数关系式。
2. 如图,在四边形中,平分,,为的中点。
(1)求证:;(2)求证:;(3)若,,求。
2. 判定定理2:_____________________________________________________________________________。
例3 如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点。
(1)证明:;(2)若正方形的边长为4,求的长。
[识记理解3]
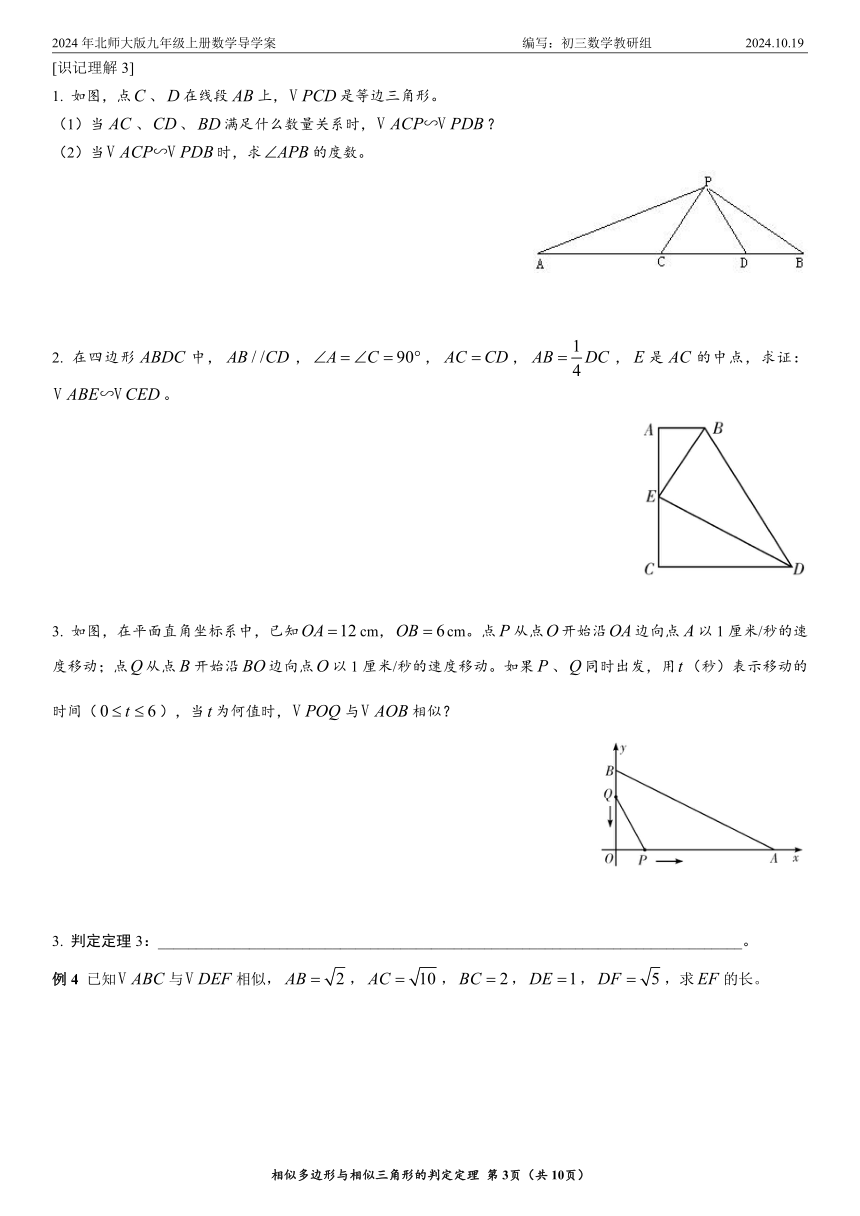
1. 如图,点、在线段上,是等边三角形。
(1)当、、满足什么数量关系时,?
(2)当时,求的度数。
2. 在四边形中,,,,,是的中点,求证:。
3. 如图,在平面直角坐标系中,已知cm,cm。点从点开始沿边向点以1厘米/秒的速度移动;点从点开始沿边向点以1厘米/秒的速度移动。如果、同时出发,用(秒)表示移动的时间(),当为何值时,与相似?
3. 判定定理3:_____________________________________________________________________________。
例4 已知与相似,,,,,,求的长。
[识记理解4]
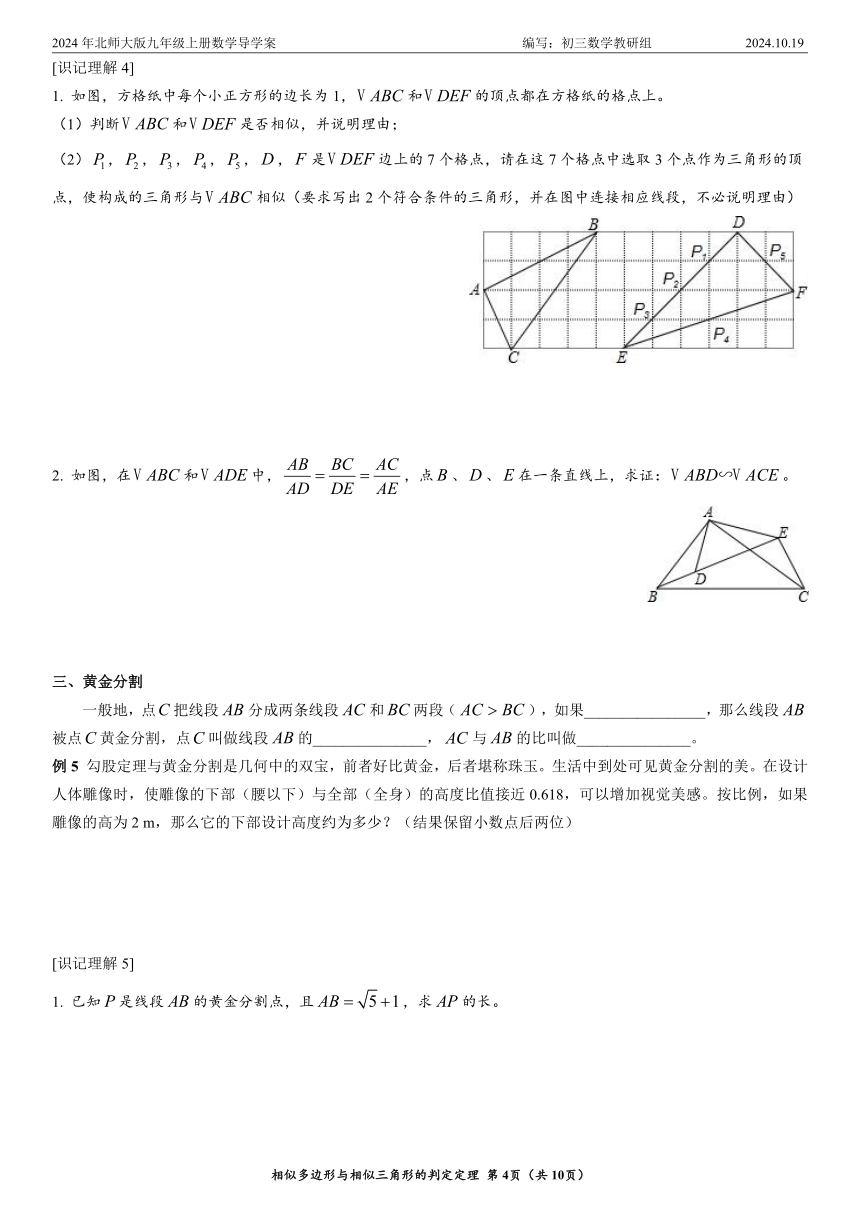
1. 如图,方格纸中每个小正方形的边长为1,和的顶点都在方格纸的格点上。
(1)判断和是否相似,并说明理由;
(2),,,,,,是边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由)
2. 如图,在和中,,点、、在一条直线上,求证:。
三、黄金分割
一般地,点把线段分成两条线段和两段(),如果________________,那么线段被点黄金分割,点叫做线段的_______________,与的比叫做_______________。
例5 勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉。生活中到处可见黄金分割的美。在设计人体雕像时,使雕像的下部(腰以下)与全部(全身)的高度比值接近0.618,可以增加视觉美感。按比例,如果雕像的高为2 m,那么它的下部设计高度约为多少?(结果保留小数点后两位)
[识记理解5]
1. 已知是线段的黄金分割点,且,求的长。
【知能提升】
一、选择题
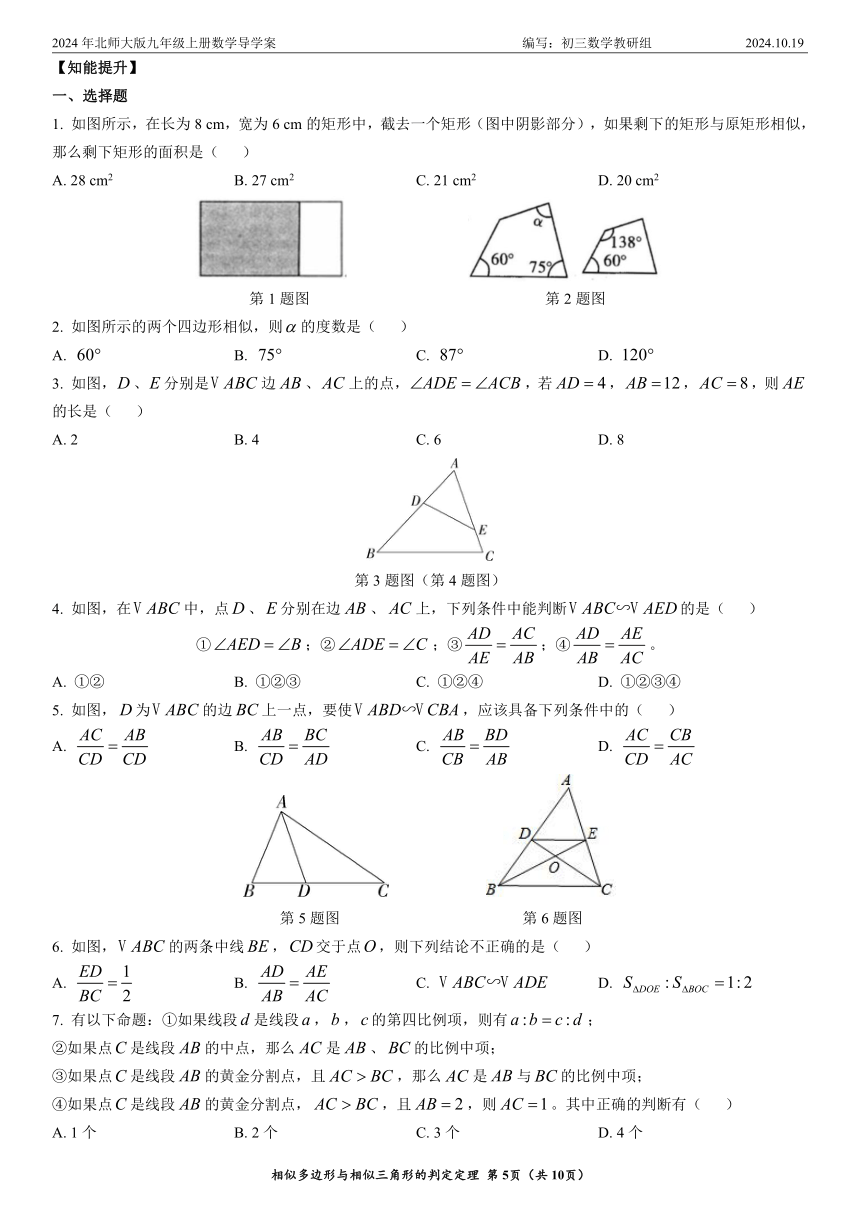
1. 如图所示,在长为8 cm,宽为6 cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A. 28 cm2 B. 27 cm2 C. 21 cm2 D. 20 cm2
第1题图 第2题图
2. 如图所示的两个四边形相似,则的度数是( )
A. B. C. D.
3. 如图,、分别是边、上的点,,若,,,则的长是( )
A. 2 B. 4 C. 6 D. 8
第3题图(第4题图)
4. 如图,在中,点、分别在边、上,下列条件中能判断的是( )
①;②;③;④。
A. ①② B. ①②③ C. ①②④ D. ①②③④
5. 如图,为的边上一点,要使,应该具备下列条件中的( )
A. B. C. D.
第5题图 第6题图
6. 如图,的两条中线,交于点,则下列结论不正确的是( )
A. B. C. D.
7. 有以下命题:①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则。其中正确的判断有( )
A. 1个 B. 2个 C. 3个 D. 4个
(2019·全国高考理科数学I卷)8. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是。若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( )
A. 165 cm B. 175 cm C. 185 cm D. 190 cm
9. 已知的三边长分别为6 cm,7.5 cm,9 cm,的一边长为4 cm,当这两个三角形相似时,的另两边长可以是( )
A. 2 cm,3 cm B. 4 cm,5 cm C. 5 cm,6 cm D. 6 cm,7 cm
10. 如图,点在上,点在上,,,下列结论正确的是( )
A. B. C. D.
第10题图
二、填空题
11. 如图,在平行四边形中,点是边上一点,且,交于点,则_______。
第11题图 第12题图
12. 如图,、交于点,于点,于点,若,,,则_______。
13. 如图,于点,于点,与交于点,,,,则______。
第13题图 第14题图
14. 如图,,,,,则的长为_________。
15. 如图,,若,,,则_________。
第15题图 第16题图
16. 如图,矩形中,,,点是边上一点,若与相似,则_______。
17. 如图,在矩形中,,,为边上的动点。当时,的长为_________。
第17题图 第18题图
18. 如图,添加一个条件:____________________,使(写出一个即可)。
19. 如图,在中,,,,点,分别在,上,将沿折叠,点的对应点刚好落在上。当时,的长为_________。
第19题图
20. 我们把宽与长的比是的矩形叫做黄金矩形。黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。已知四边形是黄金矩形,边的长度为,则该矩形的周长为__________________。
21. 在某一温度中,人体的新陈代谢水平处于最佳状态,这个温度与人体的正常体温(37 ℃)的比值正好是黄金比,那么这个使人新陈代谢水平处于最佳状态的温度约是_________℃(精确到0.1 ℃)。
22. 如图所示,顶角为的第一个黄金三角形的腰,底边与腰之比为,为第二个黄金三角形,依此类推,第2024个黄金三角形的周长为__________。
第22题图
三、解答题
23. 如图,在等边三角形中,点、分别在、上,且,求证:。
24. 如图,正方形的边长为6,点是边上的一个动点,过点作交边于点,当时,求的长。
25. 已知:如图,是边上的一点,且。求证:。
26. 如图,点、在线段上,是等边三角形,且,,。求证:。
27. 如图,点在平行四边形的边上,连接并延长与的延长线交于点。
(1)求证:;
(2)当,且时,求的长。
28. 如图,已知中,,,,点为的中点,在线段上取点,使与相似,求的长。
29. 如图,在四边形中,,相交于点,点在上,且。
(1)与相等吗?为什么?
(2)判断与是否相似,并说明理由。
30. 如图所示,在矩形中,cm,cm。点沿边从点开始向点以2 cm/s的速度移动,点沿边从点开始向点以1 cm/s的速移动,如果、同时出发,用(s)表示移动的时间()。
(1)当为何值时,为等腰直角三角形;
(2)求四边形的面积;
(3)当t为何值时,与相似。
31. 如图,在中,点在边上,且,已知,。
(I)求的度数;
(II)我们把有一个内角等于的等腰三角形称为黄金三角形。它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比。
(1)写出图中所有的黄金三角形,选一个说明理由;
(2)求的长。
相似多边形与相似三角形的判定定理 第1页(共7页)
第四章 图形的相似
§4.2 相似多边形与相似三角形的判定定理
【学习目标】
1. 掌握相似三角形和相似多边形的概念,并灵活运用相似三角形的判定定理证明和解决有关问题;
2. 掌握黄金分割的基本概念,提高运用“类比”思想的自觉性,提高推理能力。
【学习过程】
一、相似多边形的定义、判定与性质
1. 定义:各角分别______________,各边_____________的两个多边形叫做相似多边形。相似多边形的对应边的比叫做_____________,通常用_____来表示。
2. 性质:相似多边形的对应角___________,对应边_____________。
3. 判定:如果两个多边形的对应角___________,对应边的比___________,那么这两个多边形相似。
例1 如图,矩形的长,宽。
(1)如图①,若沿矩形四周有宽为2的环形区域,图中所形成的两个矩形与相似吗?请说明理由。
(2)如图②,为多少时,图中的两个矩形相似?
[识记理解1]
1. 将一张报纸对折后的半张报纸和整张报纸相似,则整张报纸的宽与长的比为多少?
二、相似三角形的判定定理
1. 判定定理1:_____________________________________________________________________________。
例2 如图,和的边、相交于点,且,点在上,求证:。
[识记理解2]
1. 如图,在正方形中,,是边上不与、重合的任意一点,于,当点在上变动时,线段也随之变化。
(1)证明:;(2)设,,求与之间的函数关系式。
2. 如图,在四边形中,平分,,为的中点。
(1)求证:;(2)求证:;(3)若,,求。
2. 判定定理2:_____________________________________________________________________________。
例3 如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点。
(1)证明:;(2)若正方形的边长为4,求的长。
[识记理解3]
1. 如图,点、在线段上,是等边三角形。
(1)当、、满足什么数量关系时,?
(2)当时,求的度数。
2. 在四边形中,,,,,是的中点,求证:。
3. 如图,在平面直角坐标系中,已知cm,cm。点从点开始沿边向点以1厘米/秒的速度移动;点从点开始沿边向点以1厘米/秒的速度移动。如果、同时出发,用(秒)表示移动的时间(),当为何值时,与相似?
3. 判定定理3:_____________________________________________________________________________。
例4 已知与相似,,,,,,求的长。
[识记理解4]
1. 如图,方格纸中每个小正方形的边长为1,和的顶点都在方格纸的格点上。
(1)判断和是否相似,并说明理由;
(2),,,,,,是边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由)
2. 如图,在和中,,点、、在一条直线上,求证:。
三、黄金分割
一般地,点把线段分成两条线段和两段(),如果________________,那么线段被点黄金分割,点叫做线段的_______________,与的比叫做_______________。
例5 勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉。生活中到处可见黄金分割的美。在设计人体雕像时,使雕像的下部(腰以下)与全部(全身)的高度比值接近0.618,可以增加视觉美感。按比例,如果雕像的高为2 m,那么它的下部设计高度约为多少?(结果保留小数点后两位)
[识记理解5]
1. 已知是线段的黄金分割点,且,求的长。
【知能提升】
一、选择题
1. 如图所示,在长为8 cm,宽为6 cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A. 28 cm2 B. 27 cm2 C. 21 cm2 D. 20 cm2
第1题图 第2题图
2. 如图所示的两个四边形相似,则的度数是( )
A. B. C. D.
3. 如图,、分别是边、上的点,,若,,,则的长是( )
A. 2 B. 4 C. 6 D. 8
第3题图(第4题图)
4. 如图,在中,点、分别在边、上,下列条件中能判断的是( )
①;②;③;④。
A. ①② B. ①②③ C. ①②④ D. ①②③④
5. 如图,为的边上一点,要使,应该具备下列条件中的( )
A. B. C. D.
第5题图 第6题图
6. 如图,的两条中线,交于点,则下列结论不正确的是( )
A. B. C. D.
7. 有以下命题:①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则。其中正确的判断有( )
A. 1个 B. 2个 C. 3个 D. 4个
(2019·全国高考理科数学I卷)8. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是。若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( )
A. 165 cm B. 175 cm C. 185 cm D. 190 cm
9. 已知的三边长分别为6 cm,7.5 cm,9 cm,的一边长为4 cm,当这两个三角形相似时,的另两边长可以是( )
A. 2 cm,3 cm B. 4 cm,5 cm C. 5 cm,6 cm D. 6 cm,7 cm
10. 如图,点在上,点在上,,,下列结论正确的是( )
A. B. C. D.
第10题图
二、填空题
11. 如图,在平行四边形中,点是边上一点,且,交于点,则_______。
第11题图 第12题图
12. 如图,、交于点,于点,于点,若,,,则_______。
13. 如图,于点,于点,与交于点,,,,则______。
第13题图 第14题图
14. 如图,,,,,则的长为_________。
15. 如图,,若,,,则_________。
第15题图 第16题图
16. 如图,矩形中,,,点是边上一点,若与相似,则_______。
17. 如图,在矩形中,,,为边上的动点。当时,的长为_________。
第17题图 第18题图
18. 如图,添加一个条件:____________________,使(写出一个即可)。
19. 如图,在中,,,,点,分别在,上,将沿折叠,点的对应点刚好落在上。当时,的长为_________。
第19题图
20. 我们把宽与长的比是的矩形叫做黄金矩形。黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。已知四边形是黄金矩形,边的长度为,则该矩形的周长为__________________。
21. 在某一温度中,人体的新陈代谢水平处于最佳状态,这个温度与人体的正常体温(37 ℃)的比值正好是黄金比,那么这个使人新陈代谢水平处于最佳状态的温度约是_________℃(精确到0.1 ℃)。
22. 如图所示,顶角为的第一个黄金三角形的腰,底边与腰之比为,为第二个黄金三角形,依此类推,第2024个黄金三角形的周长为__________。
第22题图
三、解答题
23. 如图,在等边三角形中,点、分别在、上,且,求证:。
24. 如图,正方形的边长为6,点是边上的一个动点,过点作交边于点,当时,求的长。
25. 已知:如图,是边上的一点,且。求证:。
26. 如图,点、在线段上,是等边三角形,且,,。求证:。
27. 如图,点在平行四边形的边上,连接并延长与的延长线交于点。
(1)求证:;
(2)当,且时,求的长。
28. 如图,已知中,,,,点为的中点,在线段上取点,使与相似,求的长。
29. 如图,在四边形中,,相交于点,点在上,且。
(1)与相等吗?为什么?
(2)判断与是否相似,并说明理由。
30. 如图所示,在矩形中,cm,cm。点沿边从点开始向点以2 cm/s的速度移动,点沿边从点开始向点以1 cm/s的速移动,如果、同时出发,用(s)表示移动的时间()。
(1)当为何值时,为等腰直角三角形;
(2)求四边形的面积;
(3)当t为何值时,与相似。
31. 如图,在中,点在边上,且,已知,。
(I)求的度数;
(II)我们把有一个内角等于的等腰三角形称为黄金三角形。它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比。
(1)写出图中所有的黄金三角形,选一个说明理由;
(2)求的长。
相似多边形与相似三角形的判定定理 第1页(共7页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
