6.2 反比例函数的应用及反比例函数和一次函数的结合 导学案 (无答案)北师大版(2024)数学九年级上册
文档属性
| 名称 | 6.2 反比例函数的应用及反比例函数和一次函数的结合 导学案 (无答案)北师大版(2024)数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 426.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:43:16 | ||
图片预览

文档简介
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.08.07
第六章 反比例函数
§6.2 反比例函数的应用及反比例函数和一次函数的结合
【学习目标】
1. 利用反比例函数解决实际问题,并清楚自变量的取值;
2. 进一步加深图像与函数的关系,明确两函数表达式之间的关系。
【学习过程】
一、反比例函数的简单应用
例1 学校的学生专用智能饮水机里水的温度(℃)与时间(分)之间的函数关系如图所示,当水的温度为20 ℃时,饮水机自动开始加热,当加热到100 ℃时自动停止加热(线段),随后水温开始下降,当水温降至20 ℃时(为双曲线的一部分),饮水机又自动开始加热……根据图中提供的信息,解答下列问题:
(1)分别求出饮水机里水的温度上升和下降阶段与之间的函数表达式;
(2)下课时,同学们纷纷用水杯去盛水喝。此时,饮水机里水的温度刚好达到100 ℃。据了解,饮水机1分钟可以满足12位同学的盛水要求,学生喝水的最佳温度在30 ℃~45 ℃,请问在大课间30分钟时间里有多少位同学可以盛到最佳温度的水?
[识记理解1]
为了预防疾病,某单位对办公室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例,药物燃烧后,与成反比例(如图)。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时与药物燃烧后,关于的函数关系式;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过几分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
二、反比例函数与一次函数的综合
例2 已知,反比例函数和一次函数,其中一次函数的图象经过点。
(1)试求反比例函数的表达式;
(2)若点在第一象限,且同时在上述两函数的图象上,求点的坐标。
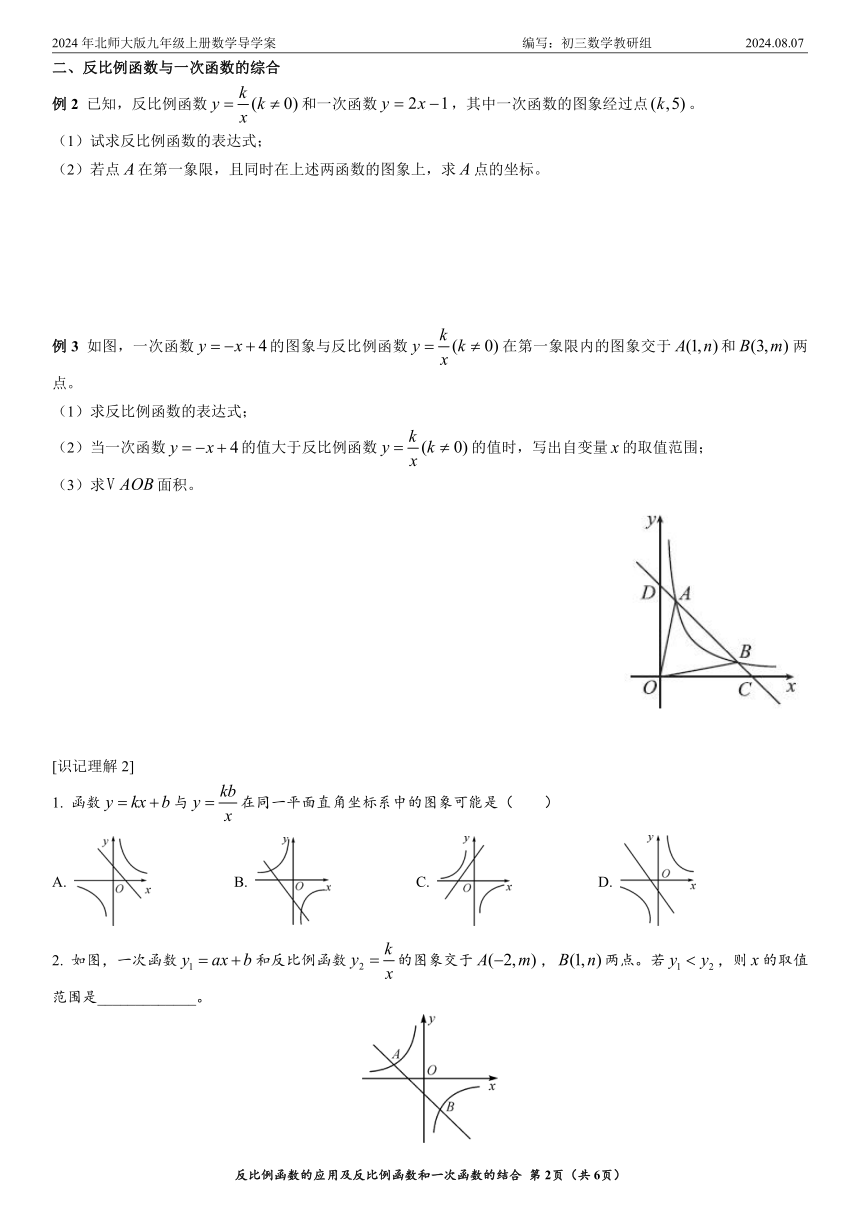
例3 如图,一次函数的图象与反比例函数在第一象限内的图象交于和两点。
(1)求反比例函数的表达式;
(2)当一次函数的值大于反比例函数的值时,写出自变量的取值范围;
(3)求面积。
[识记理解2]
1. 函数与在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
2. 如图,一次函数和反比例函数的图象交于,两点。若,则的取值范围是_____________。
【知能提升】
一、选择题
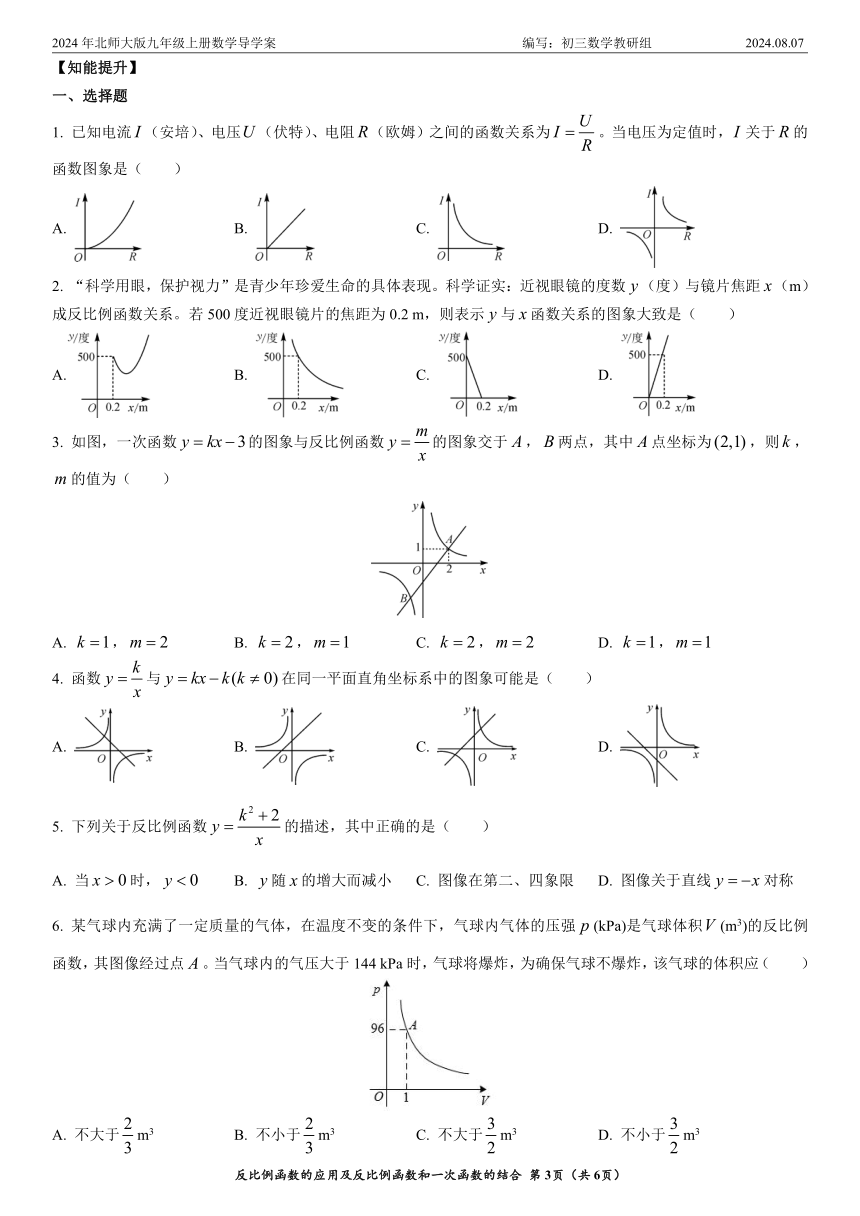
1. 已知电流(安培)、电压(伏特)、电阻(欧姆)之间的函数关系为。当电压为定值时,关于的函数图象是( )
A. B. C. D.
2. “科学用眼,保护视力”是青少年珍爱生命的具体表现。科学证实:近视眼镜的度数(度)与镜片焦距(m)成反比例函数关系。若500度近视眼镜片的焦距为0.2 m,则表示与函数关系的图象大致是( )
A. B. C. D.
3. 如图,一次函数的图象与反比例函数的图象交于,两点,其中点坐标为,则,的值为( )
A. , B. , C. , D. ,
4. 函数与在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
5. 下列关于反比例函数的描述,其中正确的是( )
A. 当时, B. 随的增大而减小 C. 图像在第二、四象限 D. 图像关于直线对称
6. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强(kPa)是气球体积(m3)的反比例函数,其图像经过点。当气球内的气压大于144 kPa时,气球将爆炸,为确保气球不爆炸,该气球的体积应( )
A. 不大于m3 B. 不小于m3 C. 不大于m3 D. 不小于m3
7. 如图,在平面直角坐标系中,直线与双曲线交于点,,若,,过点作轴,垂足为,连接,则的面积是( )
A. 2 B. C. 3 D. 6
8. 如图,正比例函数与反比例函数的图象交于,两点,轴,交轴于点,在射线上取点,且,若,则的值为( )
A. 2 B. 4 C. 6 D. 8
二、填空题
9. 已知反比例函数,当时,的取值范围是______________。
10. 我国自主研发多种新冠病毒有效用药已经用于临床救治。某新冠病毒研究团队测得成人注射一针某种药物后体内抗体浓度y(微克/mL)与注射时间天之间的函数关系如图所示(当时,与是正比例函数关系;当时,与是反比例函数关系)。则体内抗体浓度高于70微克/mL时,相应的自变量的取值范围是___________。
第10题图 第11题图
11. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点,过点作轴,垂足为,且,则以下结论:①;②当时,;③当时,;④当时,随的增大而增大,随的增大而减小。其中正确结论的是____________。
三、解答题
12. 一艘载满货物的轮船到达目的地后开始卸货,平均卸货速度(吨/天)随卸货天数(天)的变化而变化。已知与是反比例函数关系,图像如图所示。
(1)求与之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过6天卸载完毕,那么平均每天至少要卸货多少吨?
13. 已知学生注意力指标随时间(分钟)变化的函数图象如下图所示,当和时,函数图象是线段;当时,图象是反比例函数的一部分,轴。
(1)求点坐标;
(2)当满足什么条件时,学生注意力指标不低于30。
14. 如图,一次函数的图象与y轴正半轴交于点C,与反比例函数的图象交于,两点,若,点的纵坐标为3。
(1)求反比例函数的解析式;
(2)求的面积。
15. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于A,B两点。
(1)求反比例函数的表达式及点的坐标;
(2)点在轴上,连接,,若的面积为18,求满足条件的点的坐标。
16. 如图,一次函数的图象与反比例函数的图象相交于,两点,其中点的坐标为,点的坐标为。
(1)根据图象,直接写出满足的的取值范围;
(2)求这两个函数的表达式;
(3)点在线段上,且S△AOP : S△BOP=1:2,求点的坐标。
反比例函数的应用及反比例函数和一次函数的结合 第1页(共7页)
第六章 反比例函数
§6.2 反比例函数的应用及反比例函数和一次函数的结合
【学习目标】
1. 利用反比例函数解决实际问题,并清楚自变量的取值;
2. 进一步加深图像与函数的关系,明确两函数表达式之间的关系。
【学习过程】
一、反比例函数的简单应用
例1 学校的学生专用智能饮水机里水的温度(℃)与时间(分)之间的函数关系如图所示,当水的温度为20 ℃时,饮水机自动开始加热,当加热到100 ℃时自动停止加热(线段),随后水温开始下降,当水温降至20 ℃时(为双曲线的一部分),饮水机又自动开始加热……根据图中提供的信息,解答下列问题:
(1)分别求出饮水机里水的温度上升和下降阶段与之间的函数表达式;
(2)下课时,同学们纷纷用水杯去盛水喝。此时,饮水机里水的温度刚好达到100 ℃。据了解,饮水机1分钟可以满足12位同学的盛水要求,学生喝水的最佳温度在30 ℃~45 ℃,请问在大课间30分钟时间里有多少位同学可以盛到最佳温度的水?
[识记理解1]
为了预防疾病,某单位对办公室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例,药物燃烧后,与成反比例(如图)。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时与药物燃烧后,关于的函数关系式;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过几分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
二、反比例函数与一次函数的综合
例2 已知,反比例函数和一次函数,其中一次函数的图象经过点。
(1)试求反比例函数的表达式;
(2)若点在第一象限,且同时在上述两函数的图象上,求点的坐标。
例3 如图,一次函数的图象与反比例函数在第一象限内的图象交于和两点。
(1)求反比例函数的表达式;
(2)当一次函数的值大于反比例函数的值时,写出自变量的取值范围;
(3)求面积。
[识记理解2]
1. 函数与在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
2. 如图,一次函数和反比例函数的图象交于,两点。若,则的取值范围是_____________。
【知能提升】
一、选择题
1. 已知电流(安培)、电压(伏特)、电阻(欧姆)之间的函数关系为。当电压为定值时,关于的函数图象是( )
A. B. C. D.
2. “科学用眼,保护视力”是青少年珍爱生命的具体表现。科学证实:近视眼镜的度数(度)与镜片焦距(m)成反比例函数关系。若500度近视眼镜片的焦距为0.2 m,则表示与函数关系的图象大致是( )
A. B. C. D.
3. 如图,一次函数的图象与反比例函数的图象交于,两点,其中点坐标为,则,的值为( )
A. , B. , C. , D. ,
4. 函数与在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
5. 下列关于反比例函数的描述,其中正确的是( )
A. 当时, B. 随的增大而减小 C. 图像在第二、四象限 D. 图像关于直线对称
6. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强(kPa)是气球体积(m3)的反比例函数,其图像经过点。当气球内的气压大于144 kPa时,气球将爆炸,为确保气球不爆炸,该气球的体积应( )
A. 不大于m3 B. 不小于m3 C. 不大于m3 D. 不小于m3
7. 如图,在平面直角坐标系中,直线与双曲线交于点,,若,,过点作轴,垂足为,连接,则的面积是( )
A. 2 B. C. 3 D. 6
8. 如图,正比例函数与反比例函数的图象交于,两点,轴,交轴于点,在射线上取点,且,若,则的值为( )
A. 2 B. 4 C. 6 D. 8
二、填空题
9. 已知反比例函数,当时,的取值范围是______________。
10. 我国自主研发多种新冠病毒有效用药已经用于临床救治。某新冠病毒研究团队测得成人注射一针某种药物后体内抗体浓度y(微克/mL)与注射时间天之间的函数关系如图所示(当时,与是正比例函数关系;当时,与是反比例函数关系)。则体内抗体浓度高于70微克/mL时,相应的自变量的取值范围是___________。
第10题图 第11题图
11. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点,过点作轴,垂足为,且,则以下结论:①;②当时,;③当时,;④当时,随的增大而增大,随的增大而减小。其中正确结论的是____________。
三、解答题
12. 一艘载满货物的轮船到达目的地后开始卸货,平均卸货速度(吨/天)随卸货天数(天)的变化而变化。已知与是反比例函数关系,图像如图所示。
(1)求与之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过6天卸载完毕,那么平均每天至少要卸货多少吨?
13. 已知学生注意力指标随时间(分钟)变化的函数图象如下图所示,当和时,函数图象是线段;当时,图象是反比例函数的一部分,轴。
(1)求点坐标;
(2)当满足什么条件时,学生注意力指标不低于30。
14. 如图,一次函数的图象与y轴正半轴交于点C,与反比例函数的图象交于,两点,若,点的纵坐标为3。
(1)求反比例函数的解析式;
(2)求的面积。
15. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于A,B两点。
(1)求反比例函数的表达式及点的坐标;
(2)点在轴上,连接,,若的面积为18,求满足条件的点的坐标。
16. 如图,一次函数的图象与反比例函数的图象相交于,两点,其中点的坐标为,点的坐标为。
(1)根据图象,直接写出满足的的取值范围;
(2)求这两个函数的表达式;
(3)点在线段上,且S△AOP : S△BOP=1:2,求点的坐标。
反比例函数的应用及反比例函数和一次函数的结合 第1页(共7页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
