1.1 菱形的性质与判定 导学案 (无答案)北师大版(2024)数学九年级上册
文档属性
| 名称 | 1.1 菱形的性质与判定 导学案 (无答案)北师大版(2024)数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:43:43 | ||
图片预览

文档简介
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.08.09
第一章 特殊的平行四边形
§1.1 菱形的性质与判定
【学习目标】
1. 经历从现实生活中抽象出图形的过程,了解菱形的定义,并探究归纳出菱形的性质;
2. 总结归纳菱形与平行四边形的关系,掌握菱形的判定方法,发展合情的推理能力;
3. 体会菱形的轴对称性,并能运用菱形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。
【学习过程】
一、菱形的定义与性质
1. 定义:菱形是一种特殊的____________,____________________的平行四边形是菱形。
2. 性质
(1)边的性质:________________________________________________________________________。
(2)角的性质:________________________________________________________________________。
(3)对角线的性质:____________________________________________________________________。
(4)对称性:菱形是____________图形,也是____________图形。
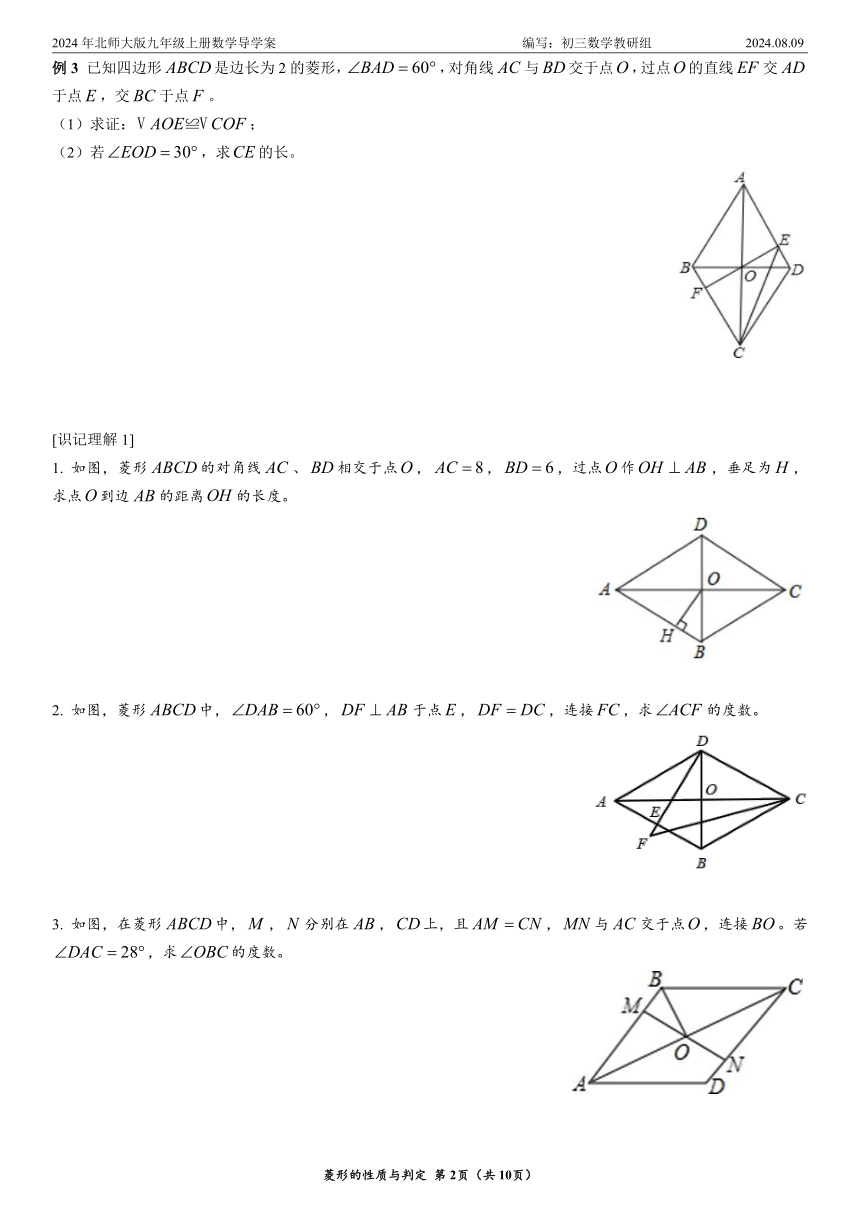
例1 如图,在菱形中,是边上一点,且。有下列结论:①;②是等边三角形;③是等腰三角形;④。若结论正确,请证明,不正确请说明理由。
例2 如图,在菱形中,,的垂直平分线交对角线于点,垂足为,连接,求的度数。
例3 已知四边形是边长为2的菱形,,对角线与交于点,过点的直线交于点,交于点。
(1)求证:;
(2)若,求的长。
[识记理解1]
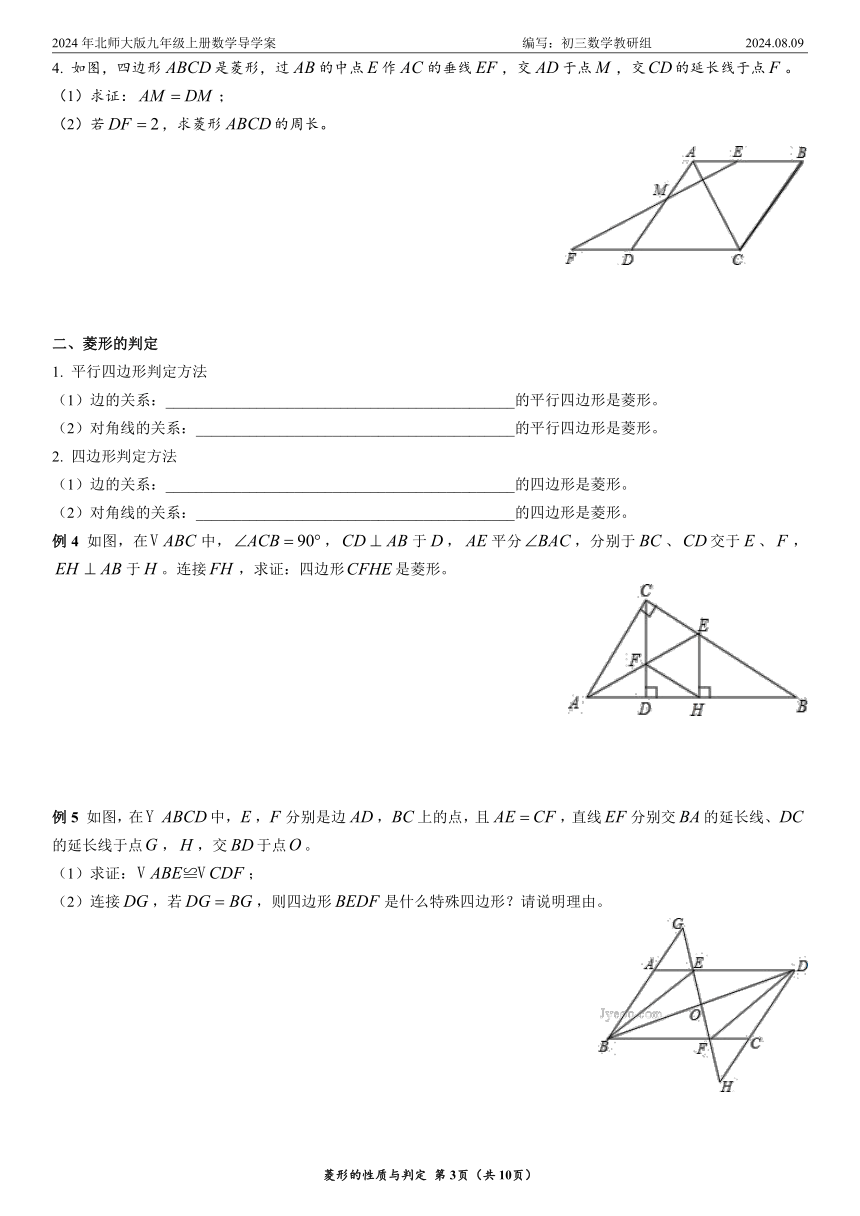
1. 如图,菱形的对角线、相交于点,,,过点作,垂足为,求点到边的距离的长度。
2. 如图,菱形中,,于点,,连接,求的度数。
3. 如图,在菱形中,,分别在,上,且,与交于点,连接。若,求的度数。
4. 如图,四边形是菱形,过的中点作的垂线,交于点,交的延长线于点。
(1)求证:;
(2)若,求菱形的周长。
二、菱形的判定
1. 平行四边形判定方法
(1)边的关系:______________________________________________的平行四边形是菱形。
(2)对角线的关系:__________________________________________的平行四边形是菱形。
2. 四边形判定方法
(1)边的关系:______________________________________________的四边形是菱形。
(2)对角线的关系:__________________________________________的四边形是菱形。
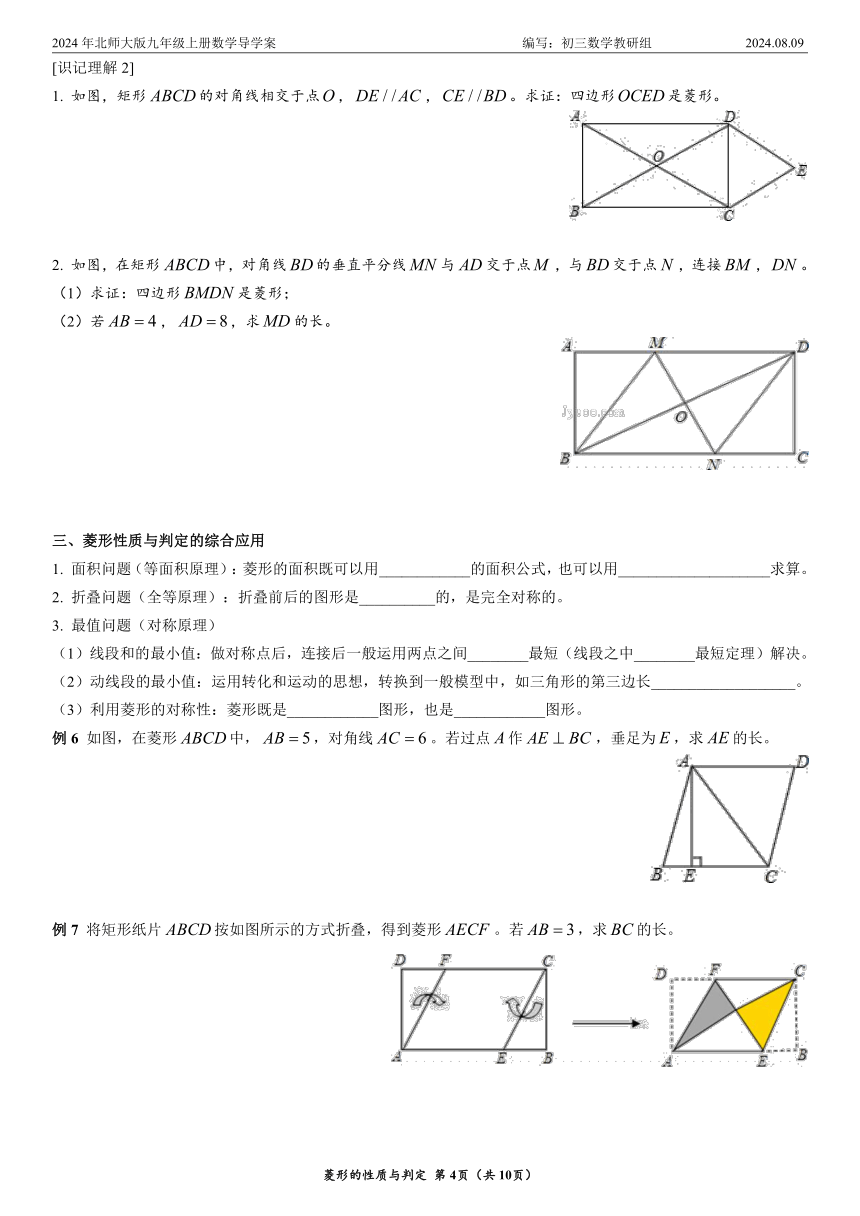
例4 如图,在中,,于,平分,分别于、交于、,于。连接,求证:四边形是菱形。
例5 如图,在中,,分别是边,上的点,且,直线分别交的延长线、的延长线于点,,交于点。
(1)求证:;
(2)连接,若,则四边形是什么特殊四边形?请说明理由。
[识记理解2]
1. 如图,矩形的对角线相交于点,,。求证:四边形是菱形。
2. 如图,在矩形中,对角线的垂直平分线与交于点,与交于点,连接,。
(1)求证:四边形是菱形;
(2)若,,求的长。
三、菱形性质与判定的综合应用
1. 面积问题(等面积原理):菱形的面积既可以用____________的面积公式,也可以用____________________求算。
2. 折叠问题(全等原理):折叠前后的图形是__________的,是完全对称的。
3. 最值问题(对称原理)
(1)线段和的最小值:做对称点后,连接后一般运用两点之间________最短(线段之中________最短定理)解决。
(2)动线段的最小值:运用转化和运动的思想,转换到一般模型中,如三角形的第三边长___________________。
(3)利用菱形的对称性:菱形既是____________图形,也是____________图形。
例6 如图,在菱形中,,对角线。若过点作,垂足为,求的长。
例7 将矩形纸片按如图所示的方式折叠,得到菱形。若,求的长。
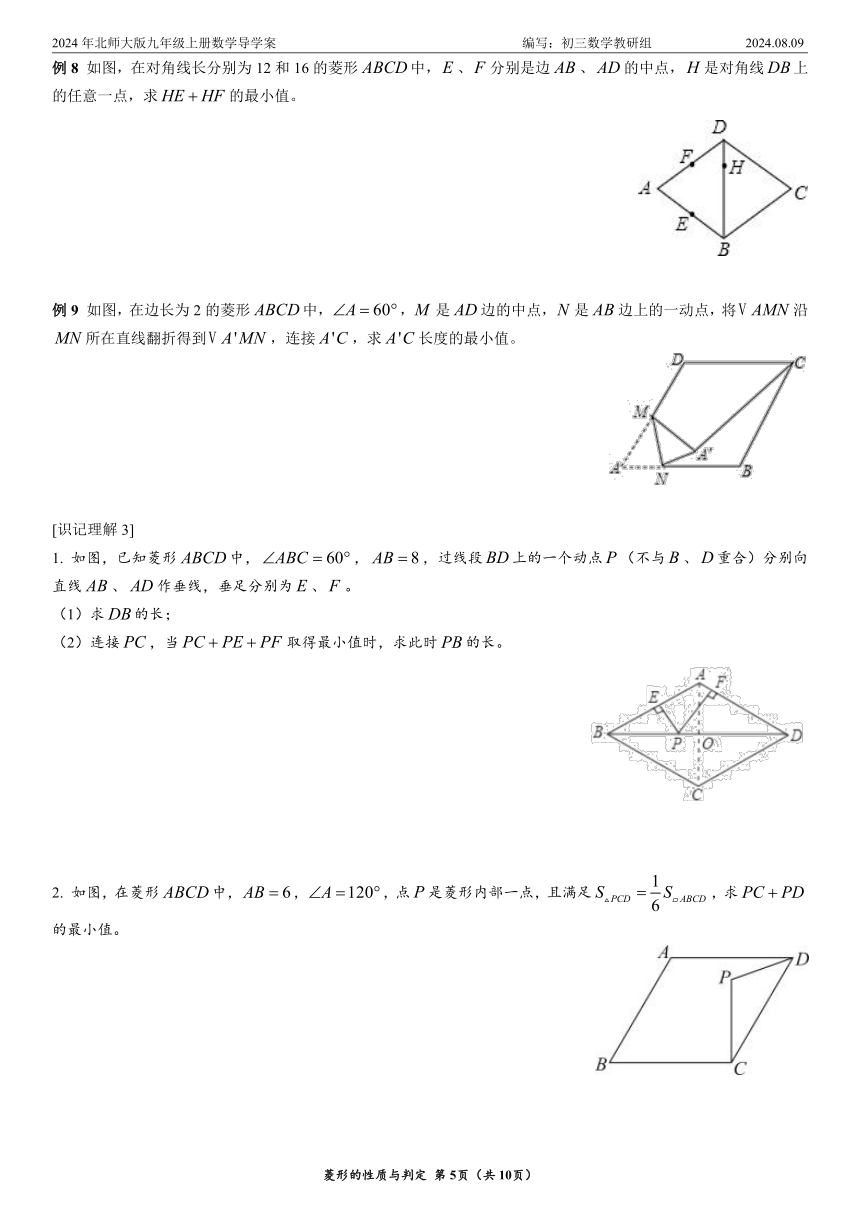
例8 如图,在对角线长分别为12和16的菱形中,、分别是边、的中点,是对角线上的任意一点,求的最小值。
例9 如图,在边长为2的菱形中,,是边的中点,是边上的一动点,将沿所在直线翻折得到,连接,求长度的最小值。
[识记理解3]
1. 如图,已知菱形中,,,过线段上的一个动点(不与、重合)分别向直线、作垂线,垂足分别为、。
(1)求的长;
(2)连接,当取得最小值时,求此时的长。
2. 如图,在菱形中,,,点是菱形内部一点,且满足,求的最小值。
【知能提升】
一、选择题
1. 已知四边形的对角线相等,顺次连接四边形的四条边中点,得到的新四边形的形状是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
2. 下列条件中,能判定平行四边形是菱形的是( )
A. 对角线互相垂直 B. 对角线相等 C. 对角线互相平分 D. 有一个角是直角
3. 如图,菱形中,对角线、交于点,为中点,菱形的周长为24,则的长等于( )
A. 12 B. 6 C. 4 D. 3
第3题图 第4题图
4. 如图,四边形是菱形,点、分别在边、上,且,。若,则的度数为( )
A. B. C. D.
5. 如图,菱形的对角线与相交于点,垂直平分,垂足为点,则的度数为( )
A. B. C. D.
第5题图 第6题图
6. 两张全等的矩形纸片,按如图方式交叉叠放在一起,,。若,,则图中重叠阴影部分的面积为( )
A. 2 B. C. D.
7. 如图,过的对角线的中点作两条互相垂直的直线,分别交,,,于,,,四点,连接,,,,下列结论正确的是( )
A. B. C. D. 四边形是菱形
第7题图 第8题图
8. 如图,在菱形中,,,点、分别在边、上,且,则的最小值是( )
A. 2 B. 3 C. D.
9. 如图,已知某广场菱形花坛的周长是24米,,则花坛对角线的长等于( )米
A. B. C. D.
第9题图 第10题图
10. 如图,与分别为的中位线与中线。在下列条件中,不能判定四边形为菱形的是( )
A. B. C. D.
11. 已知菱形的两条对角线长分别是7和8,则菱形的面积是( )
A. 56 B. 28 C. 15 D. 20
12. 如图,在菱形中,对角线、相交于点,点、分别是、的中点,连接、。若,,则的长为( )
A. B. C. D. 3
第12题图 第13题图
13. 如图,直线分别与x轴、y轴交于点、,点在线段上,线段沿翻折,点落在边上的点处。以下结论:①;②直线的解析式为;③点;④若线段上存在一点,使得以点、、、为顶点的四边形为菱形,则点的坐标是。其中正确的结论是( )
A. ①② B. ①②③ C. ①③④ D. ①②④
二、填空题
14. 如图,四边形是菱形,,,于点,是中点,连接,则的长为____________。
15. 如图,菱形中,,的垂直平分线交对角线于点,垂足为,连结,则的度数是_________。
第14题图 第15题图
16. 如图,若菱形的顶点,的坐标分别为,,点在轴上,则菱形对角线交点的坐标是_________。
第16题图 第17题图
17. 如图,菱形中,,,点是的中点,点在上,若,则线段的长为____________。
18. 如图,在菱形中,,点在上,,则的度数是____________。
第18题图 第19题图
19. 如图,在菱形中,,,点为线段上不与端点重合的一个动点。过点作直线、直线的垂线,垂足分别为、。连结,在点的运动过程中,的最小值等于___________。
20. 如图,菱形的对角线相交于点,于点,连接,,若,,则的长为____________。
第20题图 第21题图
21. 如图,△是边长为1的等边三角形,,为线段上两动点,且,过点,分别作,的平行线相交于点,分别交,于点,。现有以下结论:①;②当点与点重合时,;③;④当时,四边形为菱形。则其中正确的结论的序号是____________。
22. 已知菱形的边长为8,其中一条对角线,则另一条对角线的长为____________。
三、解答题
23. 如图,的对角线,相交于点,且,,。
(1)求证: 为菱形;
(2)过点作于点。求的长。
24. 如图,在中,是边上一点,,延长交的延长线于点,过点作交的延长线于点。求证:四边形是菱形。
25. 如图,在中,,分别是,的中点。
(1)求证:;
(2)连接,当线段与满足什么条件时,四边形是菱形?并说明理由。
26. 如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接。
(1)求证:四边形是菱形;
(2)若,,求的长。
27. 如图,在中,对角线的垂直平分线分别交、于点、,点为垂足,连接,。求证:四边形是菱形。
28. 如图,在中,点,分别为,边上的点,,。求证:平行四边形是菱形。
29. 如图,在中,平分。
(1)求证:四边形是菱形;
(2)连接交于点,延长到点,在的内部作射线,使得,过点作于点。若,,求的度数及的长。
菱形的性质与判定 第1页(共7页)
第一章 特殊的平行四边形
§1.1 菱形的性质与判定
【学习目标】
1. 经历从现实生活中抽象出图形的过程,了解菱形的定义,并探究归纳出菱形的性质;
2. 总结归纳菱形与平行四边形的关系,掌握菱形的判定方法,发展合情的推理能力;
3. 体会菱形的轴对称性,并能运用菱形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。
【学习过程】
一、菱形的定义与性质
1. 定义:菱形是一种特殊的____________,____________________的平行四边形是菱形。
2. 性质
(1)边的性质:________________________________________________________________________。
(2)角的性质:________________________________________________________________________。
(3)对角线的性质:____________________________________________________________________。
(4)对称性:菱形是____________图形,也是____________图形。
例1 如图,在菱形中,是边上一点,且。有下列结论:①;②是等边三角形;③是等腰三角形;④。若结论正确,请证明,不正确请说明理由。
例2 如图,在菱形中,,的垂直平分线交对角线于点,垂足为,连接,求的度数。
例3 已知四边形是边长为2的菱形,,对角线与交于点,过点的直线交于点,交于点。
(1)求证:;
(2)若,求的长。
[识记理解1]
1. 如图,菱形的对角线、相交于点,,,过点作,垂足为,求点到边的距离的长度。
2. 如图,菱形中,,于点,,连接,求的度数。
3. 如图,在菱形中,,分别在,上,且,与交于点,连接。若,求的度数。
4. 如图,四边形是菱形,过的中点作的垂线,交于点,交的延长线于点。
(1)求证:;
(2)若,求菱形的周长。
二、菱形的判定
1. 平行四边形判定方法
(1)边的关系:______________________________________________的平行四边形是菱形。
(2)对角线的关系:__________________________________________的平行四边形是菱形。
2. 四边形判定方法
(1)边的关系:______________________________________________的四边形是菱形。
(2)对角线的关系:__________________________________________的四边形是菱形。
例4 如图,在中,,于,平分,分别于、交于、,于。连接,求证:四边形是菱形。
例5 如图,在中,,分别是边,上的点,且,直线分别交的延长线、的延长线于点,,交于点。
(1)求证:;
(2)连接,若,则四边形是什么特殊四边形?请说明理由。
[识记理解2]
1. 如图,矩形的对角线相交于点,,。求证:四边形是菱形。
2. 如图,在矩形中,对角线的垂直平分线与交于点,与交于点,连接,。
(1)求证:四边形是菱形;
(2)若,,求的长。
三、菱形性质与判定的综合应用
1. 面积问题(等面积原理):菱形的面积既可以用____________的面积公式,也可以用____________________求算。
2. 折叠问题(全等原理):折叠前后的图形是__________的,是完全对称的。
3. 最值问题(对称原理)
(1)线段和的最小值:做对称点后,连接后一般运用两点之间________最短(线段之中________最短定理)解决。
(2)动线段的最小值:运用转化和运动的思想,转换到一般模型中,如三角形的第三边长___________________。
(3)利用菱形的对称性:菱形既是____________图形,也是____________图形。
例6 如图,在菱形中,,对角线。若过点作,垂足为,求的长。
例7 将矩形纸片按如图所示的方式折叠,得到菱形。若,求的长。
例8 如图,在对角线长分别为12和16的菱形中,、分别是边、的中点,是对角线上的任意一点,求的最小值。
例9 如图,在边长为2的菱形中,,是边的中点,是边上的一动点,将沿所在直线翻折得到,连接,求长度的最小值。
[识记理解3]
1. 如图,已知菱形中,,,过线段上的一个动点(不与、重合)分别向直线、作垂线,垂足分别为、。
(1)求的长;
(2)连接,当取得最小值时,求此时的长。
2. 如图,在菱形中,,,点是菱形内部一点,且满足,求的最小值。
【知能提升】
一、选择题
1. 已知四边形的对角线相等,顺次连接四边形的四条边中点,得到的新四边形的形状是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
2. 下列条件中,能判定平行四边形是菱形的是( )
A. 对角线互相垂直 B. 对角线相等 C. 对角线互相平分 D. 有一个角是直角
3. 如图,菱形中,对角线、交于点,为中点,菱形的周长为24,则的长等于( )
A. 12 B. 6 C. 4 D. 3
第3题图 第4题图
4. 如图,四边形是菱形,点、分别在边、上,且,。若,则的度数为( )
A. B. C. D.
5. 如图,菱形的对角线与相交于点,垂直平分,垂足为点,则的度数为( )
A. B. C. D.
第5题图 第6题图
6. 两张全等的矩形纸片,按如图方式交叉叠放在一起,,。若,,则图中重叠阴影部分的面积为( )
A. 2 B. C. D.
7. 如图,过的对角线的中点作两条互相垂直的直线,分别交,,,于,,,四点,连接,,,,下列结论正确的是( )
A. B. C. D. 四边形是菱形
第7题图 第8题图
8. 如图,在菱形中,,,点、分别在边、上,且,则的最小值是( )
A. 2 B. 3 C. D.
9. 如图,已知某广场菱形花坛的周长是24米,,则花坛对角线的长等于( )米
A. B. C. D.
第9题图 第10题图
10. 如图,与分别为的中位线与中线。在下列条件中,不能判定四边形为菱形的是( )
A. B. C. D.
11. 已知菱形的两条对角线长分别是7和8,则菱形的面积是( )
A. 56 B. 28 C. 15 D. 20
12. 如图,在菱形中,对角线、相交于点,点、分别是、的中点,连接、。若,,则的长为( )
A. B. C. D. 3
第12题图 第13题图
13. 如图,直线分别与x轴、y轴交于点、,点在线段上,线段沿翻折,点落在边上的点处。以下结论:①;②直线的解析式为;③点;④若线段上存在一点,使得以点、、、为顶点的四边形为菱形,则点的坐标是。其中正确的结论是( )
A. ①② B. ①②③ C. ①③④ D. ①②④
二、填空题
14. 如图,四边形是菱形,,,于点,是中点,连接,则的长为____________。
15. 如图,菱形中,,的垂直平分线交对角线于点,垂足为,连结,则的度数是_________。
第14题图 第15题图
16. 如图,若菱形的顶点,的坐标分别为,,点在轴上,则菱形对角线交点的坐标是_________。
第16题图 第17题图
17. 如图,菱形中,,,点是的中点,点在上,若,则线段的长为____________。
18. 如图,在菱形中,,点在上,,则的度数是____________。
第18题图 第19题图
19. 如图,在菱形中,,,点为线段上不与端点重合的一个动点。过点作直线、直线的垂线,垂足分别为、。连结,在点的运动过程中,的最小值等于___________。
20. 如图,菱形的对角线相交于点,于点,连接,,若,,则的长为____________。
第20题图 第21题图
21. 如图,△是边长为1的等边三角形,,为线段上两动点,且,过点,分别作,的平行线相交于点,分别交,于点,。现有以下结论:①;②当点与点重合时,;③;④当时,四边形为菱形。则其中正确的结论的序号是____________。
22. 已知菱形的边长为8,其中一条对角线,则另一条对角线的长为____________。
三、解答题
23. 如图,的对角线,相交于点,且,,。
(1)求证: 为菱形;
(2)过点作于点。求的长。
24. 如图,在中,是边上一点,,延长交的延长线于点,过点作交的延长线于点。求证:四边形是菱形。
25. 如图,在中,,分别是,的中点。
(1)求证:;
(2)连接,当线段与满足什么条件时,四边形是菱形?并说明理由。
26. 如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接。
(1)求证:四边形是菱形;
(2)若,,求的长。
27. 如图,在中,对角线的垂直平分线分别交、于点、,点为垂足,连接,。求证:四边形是菱形。
28. 如图,在中,点,分别为,边上的点,,。求证:平行四边形是菱形。
29. 如图,在中,平分。
(1)求证:四边形是菱形;
(2)连接交于点,延长到点,在的内部作射线,使得,过点作于点。若,,求的度数及的长。
菱形的性质与判定 第1页(共7页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
