1.2 矩形的性质与判定 导学案 (无答案)北师大版(2024)数学九年级上册
文档属性
| 名称 | 1.2 矩形的性质与判定 导学案 (无答案)北师大版(2024)数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:44:24 | ||
图片预览


文档简介
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.09.14
第一章 特殊的平行四边形
§1.2 矩形的性质与判定
【学习目标】
1. 经历从现实生活中抽象出图形的过程,了解矩形的定义,并探究归纳出矩形的性质;
2. 总结归纳矩形与平行四边形的关系,运用综合法掌握对矩形的判定,发展合情的推理能力;
3. 体会矩形的轴对称性,并能运用矩形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。
【学习过程】
一、矩形的定义与性质
1. 定义:矩形是一种特殊的____________,____________________的平行四边形是矩形。
2. 性质
(1)边的性质:________________________________________________________________________。
(2)角的性质:________________________________________________________________________。
(3)对角线的性质:____________________________________________________________________。
(4)对称性:矩形是____________图形,也是____________图形。
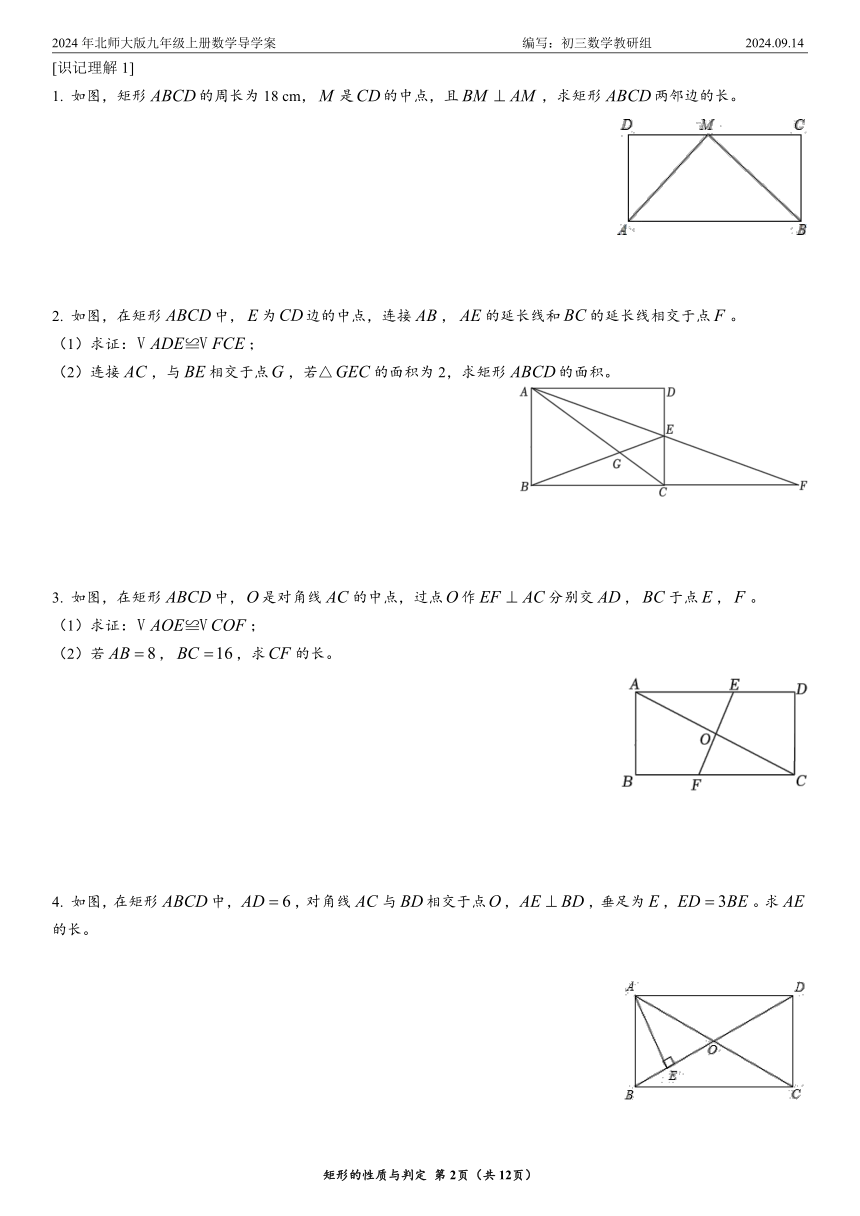
例1 如图,矩形两对角线交于点,,,求、的长及矩形的面积。
例2 如图,在矩形中,点在上,,,垂足为。
(1)求证:;
(2)若,,求的长。
例3 如图,点为矩形内一点,且。求证:。
[识记理解1]
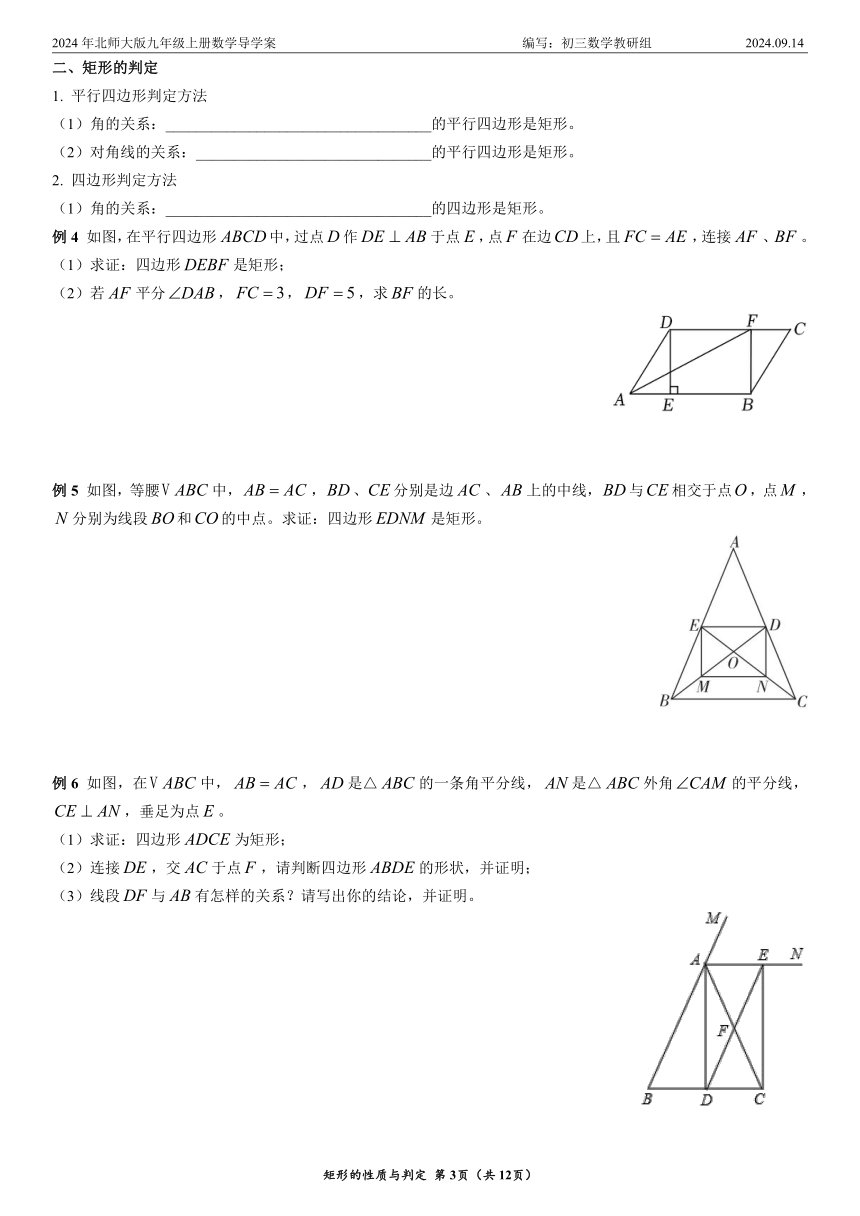
1. 如图,矩形的周长为18 cm,是的中点,且,求矩形两邻边的长。
2. 如图,在矩形中,为边的中点,连接,的延长线和的延长线相交于点。
(1)求证:;
(2)连接,与相交于点,若△的面积为2,求矩形的面积。
3. 如图,在矩形中,是对角线的中点,过点作分别交,于点,。
(1)求证:;
(2)若,,求的长。
4. 如图,在矩形中,,对角线与相交于点,,垂足为,。求的长。
二、矩形的判定
1. 平行四边形判定方法
(1)角的关系:___________________________________的平行四边形是矩形。
(2)对角线的关系:_______________________________的平行四边形是矩形。
2. 四边形判定方法
(1)角的关系:___________________________________的四边形是矩形。
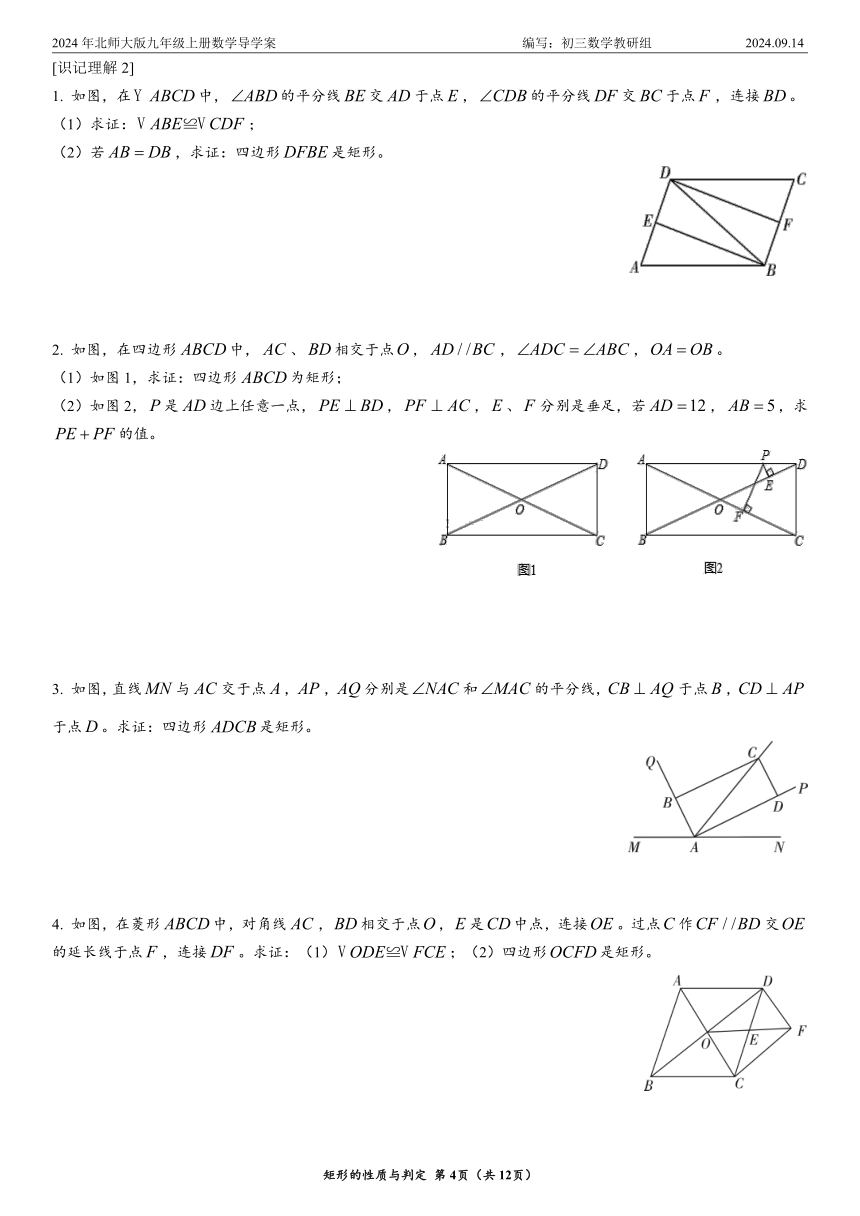
例4 如图,在平行四边形中,过点作于点,点在边上,且,连接、。
(1)求证:四边形是矩形;
(2)若平分,,,求的长。
例5 如图,等腰中,,、分别是边、上的中线,与相交于点,点,分别为线段和的中点。求证:四边形是矩形。
例6 如图,在中,,是△的一条角平分线,是△外角的平分线,,垂足为点。
(1)求证:四边形为矩形;
(2)连接,交于点,请判断四边形的形状,并证明;
(3)线段与有怎样的关系?请写出你的结论,并证明。
[识记理解2]
1. 如图,在中,的平分线交于点,的平分线交于点,连接。
(1)求证:;
(2)若,求证:四边形是矩形。
2. 如图,在四边形中,、相交于点,,,。
(1)如图1,求证:四边形为矩形;
(2)如图2,是边上任意一点,,,、分别是垂足,若,,求的值。
3. 如图,直线与交于点,,分别是和的平分线,于点,于点。求证:四边形是矩形。
4. 如图,在菱形中,对角线,相交于点,是中点,连接。过点作交的延长线于点,连接。求证:(1);(2)四边形是矩形。
三、矩形性质与判定的综合应用
1. 折叠问题(全等原理):折叠前后的图形是__________的,是完全对称的。
2. 动点问题
(1)在直角三角形中,注意特殊的角度和边,同时直角三角形斜边上的中点________________________。
(2)利用矩形的对称性:矩形既是____________图形,也是____________图形。
例7 如图,四边形是矩形,把矩形沿折叠,点落在点处,与的交点为,连接。求证:(1);(2)。
例8 如图,在矩形中,cm,、、、分别从、、、出发沿、、、方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止,已知在相同时间内,若cm(),则cm,cm,cm。
(1)当为何值时,点的运动停止;
(2)点与点可能相遇吗?点与点呢?请通过计算说明理由;
(3)当为何值时,以、Q、、为顶点的四边形是平行四边形?
例9 如图,在中,为边上的一点,是的中点,过点作的平行线交的延长线于点,且。连接。
(1)与有什么数量关系?请说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由。
[识记理解3]
1. 如图,将矩形纸片折叠,使点与点重合,折痕为,若,。求的长。
2. 如图,在矩形中,,,点是边上一点(不与、重合),连接,过点作交边于点,连接。
(1)当时,求的长;
(2)取的中点,连接,,,求的长。
3. 如图,平行四边形中,、分别为和的中点。
(1)求证:四边形是平行四边形;
(2)当的边、满足什么数量关系时,四边形是矩形,请说明理由。
【知能提升】
一、选择题
1. 在下列条件中,能够判定为矩形的是( )
A. B. C. D.
2. 下列命题为假命题的是( )
A. 两组对边分别相等的四边形是平行四边形 B. 对角线相等的平行四边形是矩形
C. 对角线互相平分且垂直的四边形是菱形 D. 一个角是直角的四边形是矩形
3. 已知在平面直角坐标系中,矩形的三个顶点的坐标为,,,则第四个顶点的坐标为( )
A. B. C. D.
4. 矩形具有而一般平行四边形不具有的性质是( )
A. 对边互相平行 B. 对边相等 C. 对角线相等 D. 对角线互相平分
5. 如图,矩形为一个正在倒水的水杯的截面图,杯中水面与的交点为,当水杯底面与水平面的夹角为时,的大小为( )
A. B. C. D.
第5题图 第6题图
6. 如图,中,是对角线、的交点,△是等边三角形,若,则平行四边形的面积是( )
A. 16 B. C. D.
7. 如图,折叠长方形的一边,使点落在边的点处,已知,,则的长是( )
A. B. 2 C. D.
第7题图 第8题图
8. 如图,四边形是矩形,,。已知,则点的坐标是( )
A. B. C. D.
9. 如图,在矩形中,cm,cm,点为上的一点,平分,则的长为( )
A. 3 cm B. 4 cm C. 5 cm D. 6 cm
10. 如图,矩形的顶点在矩形的边上,矩形的周长为10,对角线为,则图中阴影部分的面积为( )
A. 6 B. 5 C. 3 D. 10
第9题图 第10题图
11. 如图,为矩形外一点,,,则的面积是( )
A. 3 B. 4 C. 1.5 D. 2.5
第11题图 第12题图
12. 如图,在矩形中,以对角线为斜边作Rt,过点作于点,连结,若,,,则矩形的面积为( )
A. 18 B. 19 C. 20 D. 21
13. 如图,在Rt中,,为中线,点为的中点,点为的中点。若,,则的长为( )
A. 2 B. 2.5 C. 3 D. 4
第13题图 第14题图
14. 如图,在中,,,,点为边上一动点,于,于,点为中点,则的最小值为( )
A. 2.4 B. 4.8 C. 6 D. 8
15. 如图,将矩形纸片沿折叠,使点落在对角线上的处,若,则等于( )
A. B. C. D.
第15题图 第16题图
16. 如果点的坐标为,点的坐标为,则线段中点坐标为。这是小白在一本课外书上看到的一种求线段中点坐标的方法,请你利用这种方法解决下面的问题:如图,在平面直角坐标系中,矩形的顶点的坐标为,四边形是菱形,的坐标为。若直线把矩形和菱形组成的图形的面积分成相等的两部分,则直线的解析式为( )
A. B. C. D.
二、填空题
17. 如图所示,四边形为矩形,,已知,则__________。
第17题图 第18题图
18. 如图,点是矩形中边上一点,将沿折叠为,点落在上,若,则__________。
19. 如图,在矩形中,cm,cm,、分别是、的中点,则到的距离是_____cm。
第19题图 第20题图
20. 如图,点为矩形的边长上的一点,作于点,且满足。下面结论:①;②;③;④,其中正确的结论是_____________。
21.如图,在矩形中,对角线、相交于点,垂直平分交于点,若,则的长为__________。
第21题图 第22题图
22. 如图,在矩形纸片中,,,点在边上,将沿折叠,点落在点处。、分别交于点、,且,则的长为___________。
23. 如图,矩形中,,,点,,,分别在矩形各边上,且,,则四边形周长的最小值为__________。
24. 如图,点是矩形的对角线上一点,过点作,分别交、于点,,连接,,若,,则图中阴影部分的面积为__________。
第23题图 第24题图
25. 如图,在矩形中,cm,cm,点从点向点以每秒1 cm的速度运动,Q以每秒4 cm的速度从点出发,在、两点之间做往返运动,两点同时出发,点到达点为止(同时点Q也停止),当运动时间为_______________时,、Q、、四点组成矩形。
第25题图 第26题图
26. 如图,四边形是矩形,,,点在第二象限,则点的坐标是___________。
三、解答题
27. 如图,矩形的对角线、相交于点,,。
(1)求证:四边形是菱形;
(2)若,,求菱形的面积。
28. 如图,在矩形中,为对角线的中点,过点作直线分别与矩形的边,交于,两点,连接,。
(1)求证:四边形为平行四边形;
(2)若,,且,求的长。
29. 如图,在四边形中,对角线,相交于点,,,且。
(1)求证:四边形是矩形;
(2)若,,求的度数。
30. 如图,在平行四边形中,于点,延长至点,使得,连接,。
(1)求证:四边形是矩形;
(2)若,,,求的长。
31. 如图,在四边形中,,,对角线,交于点,平分交于点,连接。
(1)求证:四边形是矩形;
(2)若,求;
(3)在(2)的条件下,若,求的面积。
32. 如图,过边的中点,作,交于点,过点作,与的延长线交于点,连接,。若平分,于点。
求证:(1);(2)四边形是矩形。
33. 如图,为矩形的对角线,于点,于点。
(1)求证:;
(2)求证:四边形是平行四边形。
34. 如图,在中,对角线与相交于点,点,分别为,的中点,延长至,使,连接。
(1)求证:;
(2)当与满足什么数量关系时,四边形是矩形?请说明理由。
35. 如图,在中,,cm,cm,、是对角线上的两个动点,分别从、同时出发,相向而行,速度均为8 cm/s,运动时间为秒。
(1)若、不重合,、分别在,上,且cm,cm。求证:以、、、为顶点的四边形始终是平行四边形;
(2)若、分别是,的中点,试问当为何值时,以、、、为顶点的四边形是矩形;
(3)若、分别是折线,上的动点,分别从、开始,与、相同的速度同时出发,试问当为何值时,以、、、为顶点的四边形是菱形。
矩形的性质与判定 第1页(共7页)
第一章 特殊的平行四边形
§1.2 矩形的性质与判定
【学习目标】
1. 经历从现实生活中抽象出图形的过程,了解矩形的定义,并探究归纳出矩形的性质;
2. 总结归纳矩形与平行四边形的关系,运用综合法掌握对矩形的判定,发展合情的推理能力;
3. 体会矩形的轴对称性,并能运用矩形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。
【学习过程】
一、矩形的定义与性质
1. 定义:矩形是一种特殊的____________,____________________的平行四边形是矩形。
2. 性质
(1)边的性质:________________________________________________________________________。
(2)角的性质:________________________________________________________________________。
(3)对角线的性质:____________________________________________________________________。
(4)对称性:矩形是____________图形,也是____________图形。
例1 如图,矩形两对角线交于点,,,求、的长及矩形的面积。
例2 如图,在矩形中,点在上,,,垂足为。
(1)求证:;
(2)若,,求的长。
例3 如图,点为矩形内一点,且。求证:。
[识记理解1]
1. 如图,矩形的周长为18 cm,是的中点,且,求矩形两邻边的长。
2. 如图,在矩形中,为边的中点,连接,的延长线和的延长线相交于点。
(1)求证:;
(2)连接,与相交于点,若△的面积为2,求矩形的面积。
3. 如图,在矩形中,是对角线的中点,过点作分别交,于点,。
(1)求证:;
(2)若,,求的长。
4. 如图,在矩形中,,对角线与相交于点,,垂足为,。求的长。
二、矩形的判定
1. 平行四边形判定方法
(1)角的关系:___________________________________的平行四边形是矩形。
(2)对角线的关系:_______________________________的平行四边形是矩形。
2. 四边形判定方法
(1)角的关系:___________________________________的四边形是矩形。
例4 如图,在平行四边形中,过点作于点,点在边上,且,连接、。
(1)求证:四边形是矩形;
(2)若平分,,,求的长。
例5 如图,等腰中,,、分别是边、上的中线,与相交于点,点,分别为线段和的中点。求证:四边形是矩形。
例6 如图,在中,,是△的一条角平分线,是△外角的平分线,,垂足为点。
(1)求证:四边形为矩形;
(2)连接,交于点,请判断四边形的形状,并证明;
(3)线段与有怎样的关系?请写出你的结论,并证明。
[识记理解2]
1. 如图,在中,的平分线交于点,的平分线交于点,连接。
(1)求证:;
(2)若,求证:四边形是矩形。
2. 如图,在四边形中,、相交于点,,,。
(1)如图1,求证:四边形为矩形;
(2)如图2,是边上任意一点,,,、分别是垂足,若,,求的值。
3. 如图,直线与交于点,,分别是和的平分线,于点,于点。求证:四边形是矩形。
4. 如图,在菱形中,对角线,相交于点,是中点,连接。过点作交的延长线于点,连接。求证:(1);(2)四边形是矩形。
三、矩形性质与判定的综合应用
1. 折叠问题(全等原理):折叠前后的图形是__________的,是完全对称的。
2. 动点问题
(1)在直角三角形中,注意特殊的角度和边,同时直角三角形斜边上的中点________________________。
(2)利用矩形的对称性:矩形既是____________图形,也是____________图形。
例7 如图,四边形是矩形,把矩形沿折叠,点落在点处,与的交点为,连接。求证:(1);(2)。
例8 如图,在矩形中,cm,、、、分别从、、、出发沿、、、方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止,已知在相同时间内,若cm(),则cm,cm,cm。
(1)当为何值时,点的运动停止;
(2)点与点可能相遇吗?点与点呢?请通过计算说明理由;
(3)当为何值时,以、Q、、为顶点的四边形是平行四边形?
例9 如图,在中,为边上的一点,是的中点,过点作的平行线交的延长线于点,且。连接。
(1)与有什么数量关系?请说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由。
[识记理解3]
1. 如图,将矩形纸片折叠,使点与点重合,折痕为,若,。求的长。
2. 如图,在矩形中,,,点是边上一点(不与、重合),连接,过点作交边于点,连接。
(1)当时,求的长;
(2)取的中点,连接,,,求的长。
3. 如图,平行四边形中,、分别为和的中点。
(1)求证:四边形是平行四边形;
(2)当的边、满足什么数量关系时,四边形是矩形,请说明理由。
【知能提升】
一、选择题
1. 在下列条件中,能够判定为矩形的是( )
A. B. C. D.
2. 下列命题为假命题的是( )
A. 两组对边分别相等的四边形是平行四边形 B. 对角线相等的平行四边形是矩形
C. 对角线互相平分且垂直的四边形是菱形 D. 一个角是直角的四边形是矩形
3. 已知在平面直角坐标系中,矩形的三个顶点的坐标为,,,则第四个顶点的坐标为( )
A. B. C. D.
4. 矩形具有而一般平行四边形不具有的性质是( )
A. 对边互相平行 B. 对边相等 C. 对角线相等 D. 对角线互相平分
5. 如图,矩形为一个正在倒水的水杯的截面图,杯中水面与的交点为,当水杯底面与水平面的夹角为时,的大小为( )
A. B. C. D.
第5题图 第6题图
6. 如图,中,是对角线、的交点,△是等边三角形,若,则平行四边形的面积是( )
A. 16 B. C. D.
7. 如图,折叠长方形的一边,使点落在边的点处,已知,,则的长是( )
A. B. 2 C. D.
第7题图 第8题图
8. 如图,四边形是矩形,,。已知,则点的坐标是( )
A. B. C. D.
9. 如图,在矩形中,cm,cm,点为上的一点,平分,则的长为( )
A. 3 cm B. 4 cm C. 5 cm D. 6 cm
10. 如图,矩形的顶点在矩形的边上,矩形的周长为10,对角线为,则图中阴影部分的面积为( )
A. 6 B. 5 C. 3 D. 10
第9题图 第10题图
11. 如图,为矩形外一点,,,则的面积是( )
A. 3 B. 4 C. 1.5 D. 2.5
第11题图 第12题图
12. 如图,在矩形中,以对角线为斜边作Rt,过点作于点,连结,若,,,则矩形的面积为( )
A. 18 B. 19 C. 20 D. 21
13. 如图,在Rt中,,为中线,点为的中点,点为的中点。若,,则的长为( )
A. 2 B. 2.5 C. 3 D. 4
第13题图 第14题图
14. 如图,在中,,,,点为边上一动点,于,于,点为中点,则的最小值为( )
A. 2.4 B. 4.8 C. 6 D. 8
15. 如图,将矩形纸片沿折叠,使点落在对角线上的处,若,则等于( )
A. B. C. D.
第15题图 第16题图
16. 如果点的坐标为,点的坐标为,则线段中点坐标为。这是小白在一本课外书上看到的一种求线段中点坐标的方法,请你利用这种方法解决下面的问题:如图,在平面直角坐标系中,矩形的顶点的坐标为,四边形是菱形,的坐标为。若直线把矩形和菱形组成的图形的面积分成相等的两部分,则直线的解析式为( )
A. B. C. D.
二、填空题
17. 如图所示,四边形为矩形,,已知,则__________。
第17题图 第18题图
18. 如图,点是矩形中边上一点,将沿折叠为,点落在上,若,则__________。
19. 如图,在矩形中,cm,cm,、分别是、的中点,则到的距离是_____cm。
第19题图 第20题图
20. 如图,点为矩形的边长上的一点,作于点,且满足。下面结论:①;②;③;④,其中正确的结论是_____________。
21.如图,在矩形中,对角线、相交于点,垂直平分交于点,若,则的长为__________。
第21题图 第22题图
22. 如图,在矩形纸片中,,,点在边上,将沿折叠,点落在点处。、分别交于点、,且,则的长为___________。
23. 如图,矩形中,,,点,,,分别在矩形各边上,且,,则四边形周长的最小值为__________。
24. 如图,点是矩形的对角线上一点,过点作,分别交、于点,,连接,,若,,则图中阴影部分的面积为__________。
第23题图 第24题图
25. 如图,在矩形中,cm,cm,点从点向点以每秒1 cm的速度运动,Q以每秒4 cm的速度从点出发,在、两点之间做往返运动,两点同时出发,点到达点为止(同时点Q也停止),当运动时间为_______________时,、Q、、四点组成矩形。
第25题图 第26题图
26. 如图,四边形是矩形,,,点在第二象限,则点的坐标是___________。
三、解答题
27. 如图,矩形的对角线、相交于点,,。
(1)求证:四边形是菱形;
(2)若,,求菱形的面积。
28. 如图,在矩形中,为对角线的中点,过点作直线分别与矩形的边,交于,两点,连接,。
(1)求证:四边形为平行四边形;
(2)若,,且,求的长。
29. 如图,在四边形中,对角线,相交于点,,,且。
(1)求证:四边形是矩形;
(2)若,,求的度数。
30. 如图,在平行四边形中,于点,延长至点,使得,连接,。
(1)求证:四边形是矩形;
(2)若,,,求的长。
31. 如图,在四边形中,,,对角线,交于点,平分交于点,连接。
(1)求证:四边形是矩形;
(2)若,求;
(3)在(2)的条件下,若,求的面积。
32. 如图,过边的中点,作,交于点,过点作,与的延长线交于点,连接,。若平分,于点。
求证:(1);(2)四边形是矩形。
33. 如图,为矩形的对角线,于点,于点。
(1)求证:;
(2)求证:四边形是平行四边形。
34. 如图,在中,对角线与相交于点,点,分别为,的中点,延长至,使,连接。
(1)求证:;
(2)当与满足什么数量关系时,四边形是矩形?请说明理由。
35. 如图,在中,,cm,cm,、是对角线上的两个动点,分别从、同时出发,相向而行,速度均为8 cm/s,运动时间为秒。
(1)若、不重合,、分别在,上,且cm,cm。求证:以、、、为顶点的四边形始终是平行四边形;
(2)若、分别是,的中点,试问当为何值时,以、、、为顶点的四边形是矩形;
(3)若、分别是折线,上的动点,分别从、开始,与、相同的速度同时出发,试问当为何值时,以、、、为顶点的四边形是菱形。
矩形的性质与判定 第1页(共7页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
