9.3 用表格表示变量之间的关系 课件(共17张PPT)
文档属性
| 名称 | 9.3 用表格表示变量之间的关系 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:36:22 | ||
图片预览






文档简介
(共17张PPT)
第九章 变量之间的关系
六年级下册
3 用表格表示变量之间的关系
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
若一个长方形的周长为20 cm,一条边长为 cm(>0),面积为 cm2,则与之间满足的关系式为 .
=(10-)
新知初探
贰
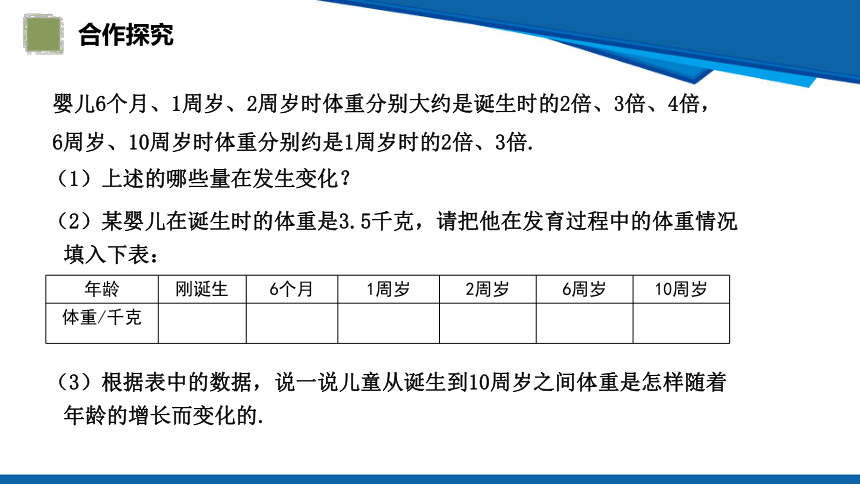
合作探究
(1)上述的哪些量在发生变化?
(2)某婴儿在诞生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
(3)根据表中的数据,说一说儿童从诞生到10周岁之间体重是怎样随着年龄的增长而变化的.
年龄 刚诞生 6个月 1周岁 2周岁 6周岁 10周岁
体重/千克
婴儿6个月、1周岁、2周岁时体重分别大约是诞生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.
典例分析
例1 一种豆子每千克的售价是2元,豆子的总售价y(元)与售出豆子的质量x(千克)之间的关系如表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)当豆子售出5千克时,总售价是 元;
(2)随着x的逐渐增大,y是怎样变化的?
(3)预测一下,当售出豆子8千克时,总售价是多少元?
10
解:(2)随着x的逐渐增大,y逐渐增大.
(3)根据规律,售出豆子的千克数乘以2即为总售价,
∴8×2=16(元),∴当售出豆子8千克时,总售价是16元.
典例分析
例2 某路公交车每月有x人次乘坐,每月的收入为y元,每人次乘坐的票价相同,下面的表格是y与x的部分数据:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 4000 5000 6000 …
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)请将表格补充完整;
解:(1)反映了收入y与人次x两个变量之间的关系,其中x是自变量,y是因变量;
(2)由表格可知:每增加500人次乘坐,每月的收入就增加1000元,表格补充如下:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 3000 4000 5000 6000 …
典例分析
例2 某路公交车每月有x人次乘坐,每月的收入为y元,每人次乘坐的票价相同,下面的表格是y与x的部分数据:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 3000 4000 5000 6000 …
(3)若该路公交车每月的支出费用为4000元,如果该路公交车每月的利润要达到10000元,则每月乘坐该路公交车要达到多少人次?(利润=收入﹣支出费用)
(3)1000÷500=2(元),(4000+10000)÷2=7000(人次).
答:每月乘坐该路公交车要达到7000人次.
当堂达标
叁
当堂达标
1.下表反映的是某地区电的使用量与应交电费之间的关系:
下列叙述错误的是( )
A.所交电费随使用量的增加而增加 B.若用电量为8千瓦时,则应交电费4.4元
C.若所交电费为2.75元,则用电量为6千瓦时 D.用电量每增加1千瓦时,电费增加0.55元
2.某公司产品的销售收入与销售量的关系如下表:
那么当销售收入为2.5万元时,销售量为 吨.
C
5
3.某河受暴雨袭击,某天此河水的水位记录为下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
(1)上表中反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
反映了时间和水位的关系.自变量:时间,因变量:水位.
4米
20到24时
课前小测
当堂达标
4.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体质量的一组对应值.
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)当所挂物体质量为3千克时,弹簧多长 不挂重物时呢
(3)若所挂重物为7千克(在允许范围内)时,你能说出此时的弹簧长度吗
解:(1)表中反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量.
(2)当所挂物体质量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米.
(3)根据表可知所挂重物为7千克(在允许范围内)时的弹簧长度=18+2×7=32(厘米).
课堂小结
肆
课堂小结
1.本节课中的量,我们主要是通过什么得到的?
2.表格在本节课中的作用是什么?
作业布置
详见教材练习题
P147 习题
谢
谢
第九章 变量之间的关系
六年级下册
3 用表格表示变量之间的关系
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
若一个长方形的周长为20 cm,一条边长为 cm(>0),面积为 cm2,则与之间满足的关系式为 .
=(10-)
新知初探
贰
合作探究
(1)上述的哪些量在发生变化?
(2)某婴儿在诞生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
(3)根据表中的数据,说一说儿童从诞生到10周岁之间体重是怎样随着年龄的增长而变化的.
年龄 刚诞生 6个月 1周岁 2周岁 6周岁 10周岁
体重/千克
婴儿6个月、1周岁、2周岁时体重分别大约是诞生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.
典例分析
例1 一种豆子每千克的售价是2元,豆子的总售价y(元)与售出豆子的质量x(千克)之间的关系如表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)当豆子售出5千克时,总售价是 元;
(2)随着x的逐渐增大,y是怎样变化的?
(3)预测一下,当售出豆子8千克时,总售价是多少元?
10
解:(2)随着x的逐渐增大,y逐渐增大.
(3)根据规律,售出豆子的千克数乘以2即为总售价,
∴8×2=16(元),∴当售出豆子8千克时,总售价是16元.
典例分析
例2 某路公交车每月有x人次乘坐,每月的收入为y元,每人次乘坐的票价相同,下面的表格是y与x的部分数据:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 4000 5000 6000 …
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)请将表格补充完整;
解:(1)反映了收入y与人次x两个变量之间的关系,其中x是自变量,y是因变量;
(2)由表格可知:每增加500人次乘坐,每月的收入就增加1000元,表格补充如下:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 3000 4000 5000 6000 …
典例分析
例2 某路公交车每月有x人次乘坐,每月的收入为y元,每人次乘坐的票价相同,下面的表格是y与x的部分数据:
x/人次 500 1000 1500 2000 2500 3000 …
y/元 1000 2000 3000 4000 5000 6000 …
(3)若该路公交车每月的支出费用为4000元,如果该路公交车每月的利润要达到10000元,则每月乘坐该路公交车要达到多少人次?(利润=收入﹣支出费用)
(3)1000÷500=2(元),(4000+10000)÷2=7000(人次).
答:每月乘坐该路公交车要达到7000人次.
当堂达标
叁
当堂达标
1.下表反映的是某地区电的使用量与应交电费之间的关系:
下列叙述错误的是( )
A.所交电费随使用量的增加而增加 B.若用电量为8千瓦时,则应交电费4.4元
C.若所交电费为2.75元,则用电量为6千瓦时 D.用电量每增加1千瓦时,电费增加0.55元
2.某公司产品的销售收入与销售量的关系如下表:
那么当销售收入为2.5万元时,销售量为 吨.
C
5
3.某河受暴雨袭击,某天此河水的水位记录为下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
(1)上表中反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
反映了时间和水位的关系.自变量:时间,因变量:水位.
4米
20到24时
课前小测
当堂达标
4.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体质量的一组对应值.
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)当所挂物体质量为3千克时,弹簧多长 不挂重物时呢
(3)若所挂重物为7千克(在允许范围内)时,你能说出此时的弹簧长度吗
解:(1)表中反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量.
(2)当所挂物体质量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米.
(3)根据表可知所挂重物为7千克(在允许范围内)时的弹簧长度=18+2×7=32(厘米).
课堂小结
肆
课堂小结
1.本节课中的量,我们主要是通过什么得到的?
2.表格在本节课中的作用是什么?
作业布置
详见教材练习题
P147 习题
谢
谢
同课章节目录
