第6章 问题解决策略:直观分析 课件(共23张PPT) 鲁教版(五四学制)(2024)数学六年级下册
文档属性
| 名称 | 第6章 问题解决策略:直观分析 课件(共23张PPT) 鲁教版(五四学制)(2024)数学六年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 11:27:47 | ||
图片预览








文档简介
(共23张PPT)
第六章 一元一次方程
六年级下册
★问题解决策略:直观分析
1.某商品原价为每件100元,降价20%后,相当于打 折出售,售价为 元,若成本为50元,则利润为 元,利润率为 。
80
30
2.某商品的进价为500元,每件售价为1000元,商店要求以40%的利润率打折出售,那么需要打 折出售此商品。
7
60%
8
课前小测
进价:购进商品时的价格(有时也叫成本价)。
售价:在销售商品时的售出价(有时称成交价,卖出价)。
标价:在销售时标出的价(有时称原价,定价)。
利润:在销售商品的过程中的纯收入,利润=售价–进价。
利润率:利润占进价的百分率,即:利润率=利润÷进价×100%。
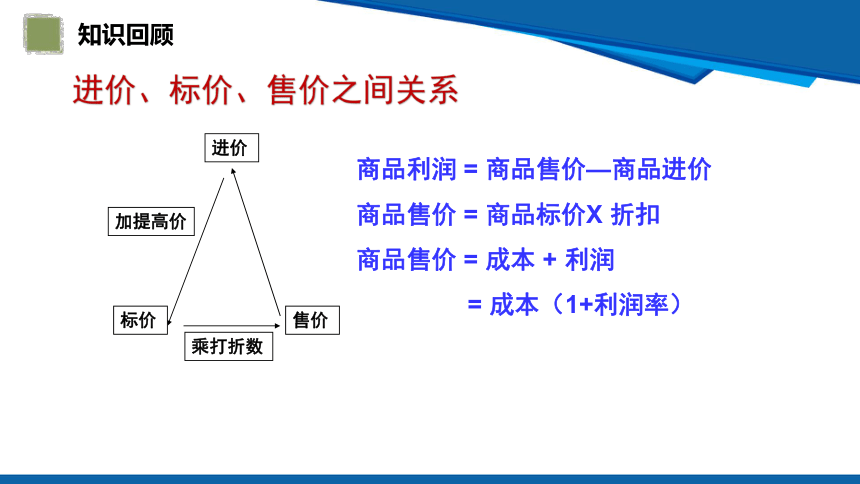
知识回顾
知识回顾
进价
售价
加提高价
标价
乘打折数
商品利润 = 商品售价—商品进价
商品售价 = 商品标价X 折扣
商品售价 = 成本 + 利润
= 成本(1+利润率)
进价、标价、售价之间关系
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
观察下面的图形与文字,说说你的想法.
1.道路标志多数用的是图形,为什么?
因为人们对图表的理解和记忆能力超过单纯的文字,这是由大脑的特点决定的.
2.实际上,借助图表直观分析数量关系,往往是解决问题的一种重要策略.
新知初探
贰
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
合作探究
【理解问题】
(1)这个问题中涉及哪些量?哪些是已知量?哪些是未知量?
每件服装的成本价、标价、售价、利润;利润是已知量,成本价、标价和售价是未知量.
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
合作探究
【理解问题】
(2)你能用文字语言描述这个问题中所蕴含的等量关系吗?
(3)采用什么方式可以更清楚地展示这个问题中各个量之间的关系?
可以借助图表来表示它们之间的关系.
服装的成本价提价后等于标价,标价再打折后等于售价,售价与成本价的差等于利润.
合作探究
【拟订计划】
(1)想象一下商店从进货、标价到销售获利的过程,你能用示意图直观地表示这一过程吗?
(2)根据示意图,你能写出哪些等量关系?
成本价×(1+40%)=标价,标价×80%=售价,售价-成本价=利润.
(3)设这种服装每件的成本为元,你能用含的代数式表示其他量吗?根据自己写出的等量关系,你能列出怎样的方程?
标价为(1+40%),售价为(1+40%)·80%,可列出方程:(1+40%)·80%-=15.
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
【解决问题】解:设每件服装的成本价为x元,根据题意,
每件服装的标价为:_______________。
每件服装的实际售价为:_______________。
每件服装的利润为:_____________________。
因此,列出方程为:______________________。
解方程,得x=_____。
因此每件服装的成本价是:_____元。
(1+40%)·x
(1+40%) ·x ·80%
(1+40%) ·x ·80%-x
(1+40%) ·x ·80%-x=15
125
125
合作探究
【实施计划】
例1 某商场将某种商品按原价的8折出售,此时商品的利润率是10%,此商品的进价为1800元,那么商品的原价是多少?
解:设该商品的原价为x元,根据题意,
每件商品的实际售价为:________。
每件商品的利润为:_____________。
因此,列出方程为:_________________。
解方程,得x=_____。
因此这种商品的原价是:_____元。
80%x
80% -1800
2475
2475
每件商品的利润率为:_______________。
典例分析
分析:销售的盈亏取决于总售价与总成本(两件衣服的成本之和)的关系。
总售价(120元) > 总成本
总售价(120元) < 总成本
总售价(120元) = 总成本
盈 利
亏 损
不盈不亏
例2 一商店以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
典例分析
设亏损25%的衣服进价是 y元,
根据题意,得 y-0.25y=60。
解得 y=80。
设盈利25%的衣服进价是 x 元,
根据题意,得 x+0.25 x=60,
解得 x=48。
解:
两件衣服总成本为x+y=48+80=128 (元)。
因为60+60=120(元),120-128=-8(元),
所以卖这两件衣服共亏损了8元。
典例分析
典例分析
例3 某单位的四幢宿舍楼在一条直线上,现要在这四幢宿舍楼之间建一个超市,使得四幢宿舍楼到超市的距离之和最短.超市应建在什么位置
解:画图分析如下:
假设四幢宿舍楼分别为点A,B,C,D,超市为点E,四幢宿舍楼到超市的距离之和即为AE+BE+CE+DE.分三种情况讨论:
①如图,当点E1位于AB上时,AE1+BE1+CE1+DE1=AD+BC+2BE1,容易发现此时当BE1最小时,距离之和最短,即当点E1位于点B时,距离之和最短为AD+BC.
②如图,当点E2位于BC上时,AE2+BE2+CE2+DE2=AD+BC.
③如图,当点E3位于CD上时,AE3+BE3+CE3+DE3=AD+BC+2CE3,容易发现此时当CE3最小时,距离之和最短,即当点E3位于点C时,距离之和最短为AD+BC.
综上,超市应建在线段BC上,即中间两幢宿舍楼连线所构成的线段上.
当堂达标
叁
当堂达标
1.某商品的进价为200元,销售价为260元,后又折价销售,所得利润率为4%,此商品是按原售价的几折销售的?
解:设商品是按原售价的折销售的,根据题意,得
(260×-200)÷200= 4%.
解得=8.
答:此商品是按原售价的8折销售的.
当堂达标
2.五个人聚会,如果每两个人要握一次手,那么五个人共握多少次手?
解:画图分析如下:
将五个人分别看作在一条直线上的五个点,五个人总共握手的次数即为每两点之间不同线段的条数。由图可知不同线段的条数为4+3+2+1=10,所以五个人共握10次手。
课堂小结
肆
= 商品售价—商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
问
题
课堂小结
1.在利用一元一次方程解决问题时,借助图表分析对解决这类问题的作用是什么?
2.销售问题中的相关知识
作业布置
详见教材练习题
P61习题2,4.5
谢
谢
第六章 一元一次方程
六年级下册
★问题解决策略:直观分析
1.某商品原价为每件100元,降价20%后,相当于打 折出售,售价为 元,若成本为50元,则利润为 元,利润率为 。
80
30
2.某商品的进价为500元,每件售价为1000元,商店要求以40%的利润率打折出售,那么需要打 折出售此商品。
7
60%
8
课前小测
进价:购进商品时的价格(有时也叫成本价)。
售价:在销售商品时的售出价(有时称成交价,卖出价)。
标价:在销售时标出的价(有时称原价,定价)。
利润:在销售商品的过程中的纯收入,利润=售价–进价。
利润率:利润占进价的百分率,即:利润率=利润÷进价×100%。
知识回顾
知识回顾
进价
售价
加提高价
标价
乘打折数
商品利润 = 商品售价—商品进价
商品售价 = 商品标价X 折扣
商品售价 = 成本 + 利润
= 成本(1+利润率)
进价、标价、售价之间关系
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
观察下面的图形与文字,说说你的想法.
1.道路标志多数用的是图形,为什么?
因为人们对图表的理解和记忆能力超过单纯的文字,这是由大脑的特点决定的.
2.实际上,借助图表直观分析数量关系,往往是解决问题的一种重要策略.
新知初探
贰
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
合作探究
【理解问题】
(1)这个问题中涉及哪些量?哪些是已知量?哪些是未知量?
每件服装的成本价、标价、售价、利润;利润是已知量,成本价、标价和售价是未知量.
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
合作探究
【理解问题】
(2)你能用文字语言描述这个问题中所蕴含的等量关系吗?
(3)采用什么方式可以更清楚地展示这个问题中各个量之间的关系?
可以借助图表来表示它们之间的关系.
服装的成本价提价后等于标价,标价再打折后等于售价,售价与成本价的差等于利润.
合作探究
【拟订计划】
(1)想象一下商店从进货、标价到销售获利的过程,你能用示意图直观地表示这一过程吗?
(2)根据示意图,你能写出哪些等量关系?
成本价×(1+40%)=标价,标价×80%=售价,售价-成本价=利润.
(3)设这种服装每件的成本为元,你能用含的代数式表示其他量吗?根据自己写出的等量关系,你能列出怎样的方程?
标价为(1+40%),售价为(1+40%)·80%,可列出方程:(1+40%)·80%-=15.
问题: 一家商店将某种服装按成本价提高40%后标价,又以八折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
【解决问题】解:设每件服装的成本价为x元,根据题意,
每件服装的标价为:_______________。
每件服装的实际售价为:_______________。
每件服装的利润为:_____________________。
因此,列出方程为:______________________。
解方程,得x=_____。
因此每件服装的成本价是:_____元。
(1+40%)·x
(1+40%) ·x ·80%
(1+40%) ·x ·80%-x
(1+40%) ·x ·80%-x=15
125
125
合作探究
【实施计划】
例1 某商场将某种商品按原价的8折出售,此时商品的利润率是10%,此商品的进价为1800元,那么商品的原价是多少?
解:设该商品的原价为x元,根据题意,
每件商品的实际售价为:________。
每件商品的利润为:_____________。
因此,列出方程为:_________________。
解方程,得x=_____。
因此这种商品的原价是:_____元。
80%x
80% -1800
2475
2475
每件商品的利润率为:_______________。
典例分析
分析:销售的盈亏取决于总售价与总成本(两件衣服的成本之和)的关系。
总售价(120元) > 总成本
总售价(120元) < 总成本
总售价(120元) = 总成本
盈 利
亏 损
不盈不亏
例2 一商店以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
典例分析
设亏损25%的衣服进价是 y元,
根据题意,得 y-0.25y=60。
解得 y=80。
设盈利25%的衣服进价是 x 元,
根据题意,得 x+0.25 x=60,
解得 x=48。
解:
两件衣服总成本为x+y=48+80=128 (元)。
因为60+60=120(元),120-128=-8(元),
所以卖这两件衣服共亏损了8元。
典例分析
典例分析
例3 某单位的四幢宿舍楼在一条直线上,现要在这四幢宿舍楼之间建一个超市,使得四幢宿舍楼到超市的距离之和最短.超市应建在什么位置
解:画图分析如下:
假设四幢宿舍楼分别为点A,B,C,D,超市为点E,四幢宿舍楼到超市的距离之和即为AE+BE+CE+DE.分三种情况讨论:
①如图,当点E1位于AB上时,AE1+BE1+CE1+DE1=AD+BC+2BE1,容易发现此时当BE1最小时,距离之和最短,即当点E1位于点B时,距离之和最短为AD+BC.
②如图,当点E2位于BC上时,AE2+BE2+CE2+DE2=AD+BC.
③如图,当点E3位于CD上时,AE3+BE3+CE3+DE3=AD+BC+2CE3,容易发现此时当CE3最小时,距离之和最短,即当点E3位于点C时,距离之和最短为AD+BC.
综上,超市应建在线段BC上,即中间两幢宿舍楼连线所构成的线段上.
当堂达标
叁
当堂达标
1.某商品的进价为200元,销售价为260元,后又折价销售,所得利润率为4%,此商品是按原售价的几折销售的?
解:设商品是按原售价的折销售的,根据题意,得
(260×-200)÷200= 4%.
解得=8.
答:此商品是按原售价的8折销售的.
当堂达标
2.五个人聚会,如果每两个人要握一次手,那么五个人共握多少次手?
解:画图分析如下:
将五个人分别看作在一条直线上的五个点,五个人总共握手的次数即为每两点之间不同线段的条数。由图可知不同线段的条数为4+3+2+1=10,所以五个人共握10次手。
课堂小结
肆
= 商品售价—商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
问
题
课堂小结
1.在利用一元一次方程解决问题时,借助图表分析对解决这类问题的作用是什么?
2.销售问题中的相关知识
作业布置
详见教材练习题
P61习题2,4.5
谢
谢
同课章节目录
