用空间向量求空间角
图片预览


文档简介
课件13张PPT。3.2立体几何中的向量方法(3)
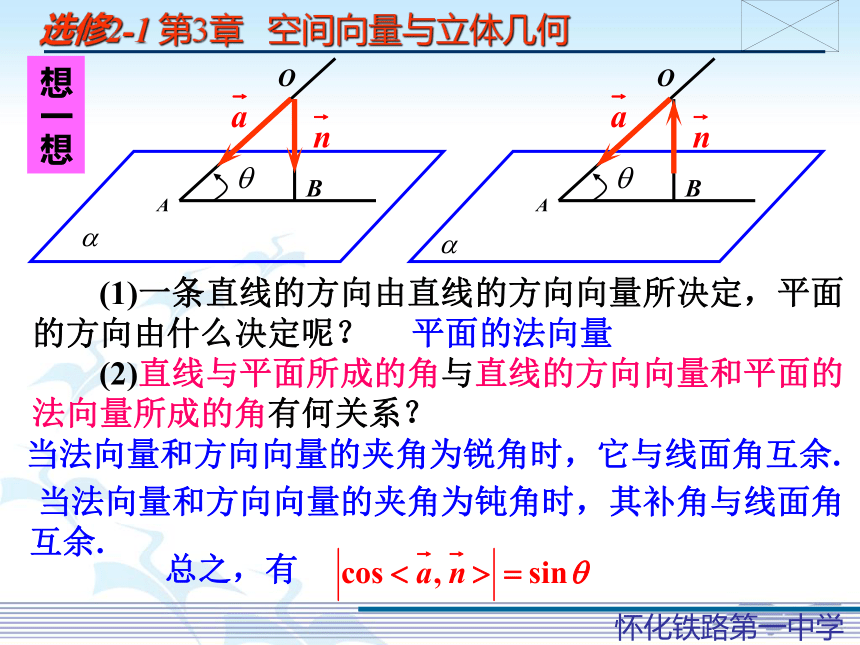
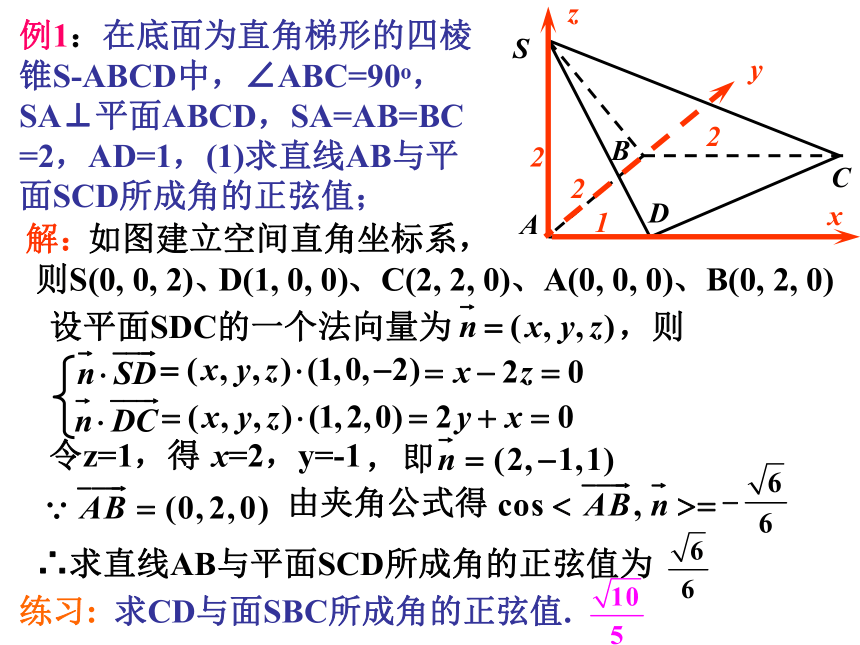
空间向量与空间角(一)一、用空间向量求直线与平面所成的角 一个平面的斜线和它在这个平面内的射影的夹角,叫做斜线和平面所成的角,也叫斜线和平面的夹角.直线和平面所成角的定义:直线和平面垂直,则直线和平面所成的角是直线和平面平行或在平面内,则直线和平面所成的角是直线和平面所成的角的范围是 (1)一条直线的方向由直线的方向向量所决定,平面的方向由什么决定呢?想一想平面的法向量 (2)直线与平面所成的角与直线的方向向量和平面的法向量所成的角有何关系?当法向量和方向向量的夹角为锐角时,它与线面角互余. 当法向量和方向向量的夹角为钝角时,其补角与线面角互余.总之,有SABC222例1:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90o,SA⊥平面ABCD,SA=AB=BC
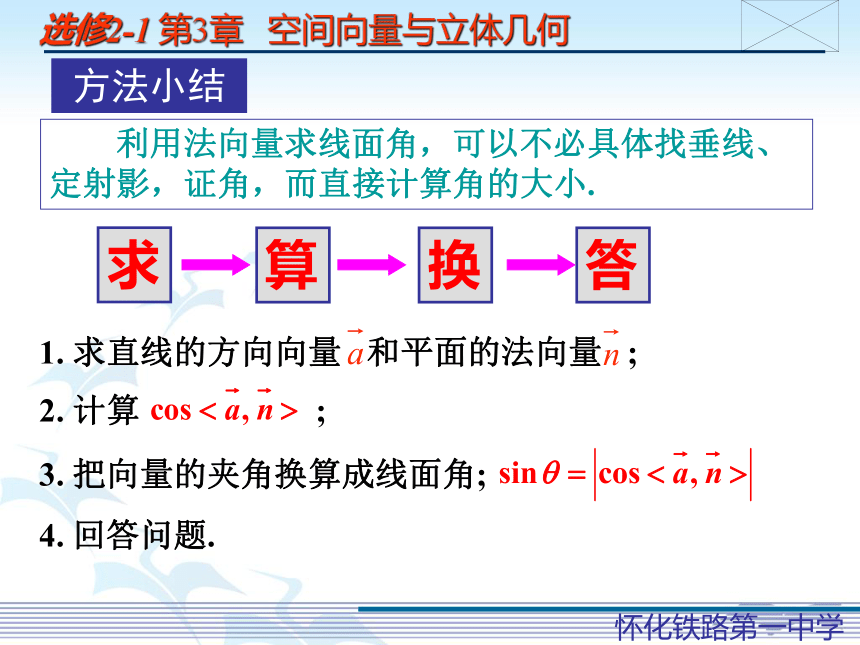
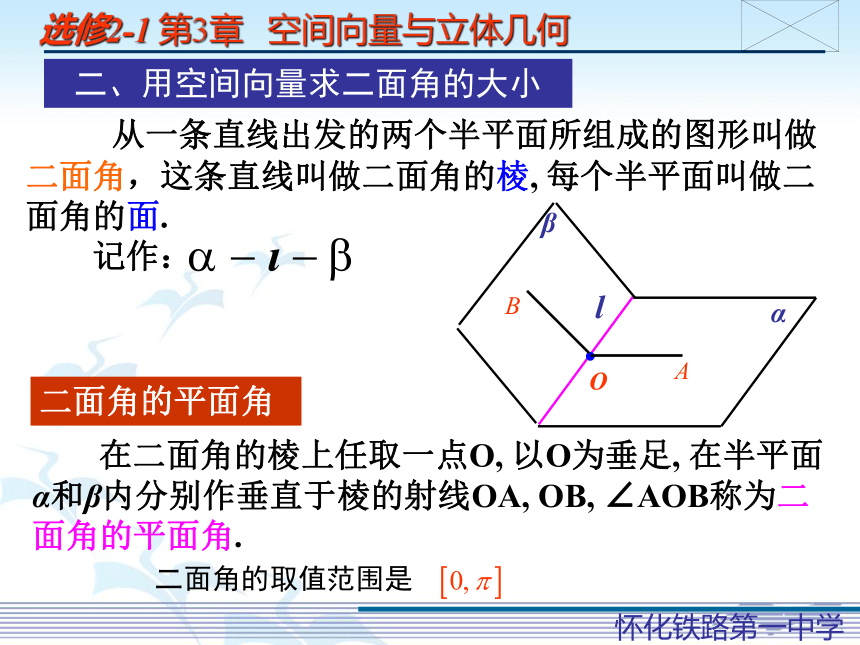
=2,AD=1,(1)求直线AB与平面SCD所成角的正弦值;D1解: 如图建立空间直角坐标系,xyz则S(0, 0, 2)、D(1, 0, 0)、C(2, 2, 0)、A(0, 0, 0)、B(0, 2, 0)设平面SDC的一个法向量为,则令z=1,得x=2,y=-1由夹角公式得∴求直线AB与平面SCD所成角的正弦值为练习: 求CD与面SBC所成角的正弦值.方法小结 利用法向量求线面角,可以不必具体找垂线、定射影,证角,而直接计算角的大小.4. 回答问题.1. 求直线的方向向量 和平面的法向量 ;2. 计算 ;3. 把向量的夹角换算成线面角;二、用空间向量求二面角的大小 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱, 每个半平面叫做二面角的面.
记作:二面角的平面角 在二面角的棱上任取一点O, 以O为垂足, 在半平面α和β内分别作垂直于棱的射线OA, OB, ∠AOB称为二面角的平面角.二面角的取值范围是<必修2>是如何求二面角的大小?1、找到或作出二面角的平面角;2、证明 1中的角就是所求的角;3、计算出此角的大小;4、回答问题.可以用平面的法向量求二面角的大小吗?平面的方向由其法向量所决定,二面角的大小与它们的法向量的夹角大小由什么关系呢? 两法向量同进同出,则两法向量的夹角与二面角互补; 两法向量一进一出,则两法向量的夹角与二面角相等;
探求解:设AB=1,则设平面CDB1的一个法向量为则显然平面ABC的一个法向量是夹角公式得故截面B1CD和底面ABC所成角的余弦值为例2:直棱 柱ABC-A1B1C1中AA1=2AB
=2BC=2CA,D为AA1中点,求平面AB C与平面B1CD所成角的余弦值. 设E、E1分别为AB、A1B1的中点,A1B1C1ABCDEE1如图建立空间直角坐标系,xyzSABD2221练习:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90o,SA⊥平面ABCD,SA=AB=BC=2,AD=1,求平面SBC与平面SCD所成的角.C求得平面SDC的一个法向量为平面SBC的一个法向量为∴ 平面SBC⊥平面SCD 方法小结 1. 求两个平面的法向量;2. 计算两个法向量的夹角的余弦值;3. 把向量的夹角换算成二面角的余弦值;如果能直观判断是锐角还是钝角? 就直接写;一个平面如果存在垂线,就不用待定系数法求法向量.如果不能判断是锐角还是钝角? 就看法向量的方向:同进同出,则互补;一进一出,就相等.4. 回答问题.三、归纳总结 利用向量求空间角的优势在于它是“一般方法” 利用向量求空间角可以不必因题制宜地采取各种技巧、方法去寻求、证明、计算对应的平面角,而采用统一的方法、步骤去计算出空间角.其不足是(1)相对而言,有时计算繁杂; (2)此方法一般需建立空间直角坐标系,而对于不便建系的图形,该方法失效或计算量大幅上升.再见!
空间向量与空间角(一)一、用空间向量求直线与平面所成的角 一个平面的斜线和它在这个平面内的射影的夹角,叫做斜线和平面所成的角,也叫斜线和平面的夹角.直线和平面所成角的定义:直线和平面垂直,则直线和平面所成的角是直线和平面平行或在平面内,则直线和平面所成的角是直线和平面所成的角的范围是 (1)一条直线的方向由直线的方向向量所决定,平面的方向由什么决定呢?想一想平面的法向量 (2)直线与平面所成的角与直线的方向向量和平面的法向量所成的角有何关系?当法向量和方向向量的夹角为锐角时,它与线面角互余. 当法向量和方向向量的夹角为钝角时,其补角与线面角互余.总之,有SABC222例1:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90o,SA⊥平面ABCD,SA=AB=BC
=2,AD=1,(1)求直线AB与平面SCD所成角的正弦值;D1解: 如图建立空间直角坐标系,xyz则S(0, 0, 2)、D(1, 0, 0)、C(2, 2, 0)、A(0, 0, 0)、B(0, 2, 0)设平面SDC的一个法向量为,则令z=1,得x=2,y=-1由夹角公式得∴求直线AB与平面SCD所成角的正弦值为练习: 求CD与面SBC所成角的正弦值.方法小结 利用法向量求线面角,可以不必具体找垂线、定射影,证角,而直接计算角的大小.4. 回答问题.1. 求直线的方向向量 和平面的法向量 ;2. 计算 ;3. 把向量的夹角换算成线面角;二、用空间向量求二面角的大小 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱, 每个半平面叫做二面角的面.
记作:二面角的平面角 在二面角的棱上任取一点O, 以O为垂足, 在半平面α和β内分别作垂直于棱的射线OA, OB, ∠AOB称为二面角的平面角.二面角的取值范围是<必修2>是如何求二面角的大小?1、找到或作出二面角的平面角;2、证明 1中的角就是所求的角;3、计算出此角的大小;4、回答问题.可以用平面的法向量求二面角的大小吗?平面的方向由其法向量所决定,二面角的大小与它们的法向量的夹角大小由什么关系呢? 两法向量同进同出,则两法向量的夹角与二面角互补; 两法向量一进一出,则两法向量的夹角与二面角相等;
探求解:设AB=1,则设平面CDB1的一个法向量为则显然平面ABC的一个法向量是夹角公式得故截面B1CD和底面ABC所成角的余弦值为例2:直棱 柱ABC-A1B1C1中AA1=2AB
=2BC=2CA,D为AA1中点,求平面AB C与平面B1CD所成角的余弦值. 设E、E1分别为AB、A1B1的中点,A1B1C1ABCDEE1如图建立空间直角坐标系,xyzSABD2221练习:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90o,SA⊥平面ABCD,SA=AB=BC=2,AD=1,求平面SBC与平面SCD所成的角.C求得平面SDC的一个法向量为平面SBC的一个法向量为∴ 平面SBC⊥平面SCD 方法小结 1. 求两个平面的法向量;2. 计算两个法向量的夹角的余弦值;3. 把向量的夹角换算成二面角的余弦值;如果能直观判断是锐角还是钝角? 就直接写;一个平面如果存在垂线,就不用待定系数法求法向量.如果不能判断是锐角还是钝角? 就看法向量的方向:同进同出,则互补;一进一出,就相等.4. 回答问题.三、归纳总结 利用向量求空间角的优势在于它是“一般方法” 利用向量求空间角可以不必因题制宜地采取各种技巧、方法去寻求、证明、计算对应的平面角,而采用统一的方法、步骤去计算出空间角.其不足是(1)相对而言,有时计算繁杂; (2)此方法一般需建立空间直角坐标系,而对于不便建系的图形,该方法失效或计算量大幅上升.再见!
