【课堂无忧】人教版四下4.10《小数的近似数》(课件)
文档属性
| 名称 | 【课堂无忧】人教版四下4.10《小数的近似数》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 00:00:00 | ||
图片预览



文档简介
(共38张PPT)
4.10
小数的近似数
(人教版)四年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
结合具体情境理解小数近似数的意义,掌握求小数近似数的方法,会应用“四舍五入”法求小数的近似数,知道精确度的含义。
01
02
经历求小数近似数的过程,通过测量、观察、发现等活动培养推理及概括能力,初步掌握“迁移”和“数形结合”等数学思想方法。
03
感受近似数的实际意义,体会数学与生活的密切联系,激发学习兴趣,培养学生的数感。
02
新知导入
李叔叔在超市买一个电饭煲和一个电饼铛。
电饭煲307元 电饼铛197元
李叔叔大约花了多少钱?估一估,算一算。
02
新知导入
李叔叔在超市买一个电饭煲和一个电饼铛。李叔叔大约花了多少钱?估一估,算一算
把307看作300,把197看作200。
300+200=500(元)
准确数
近似数
02
新知导入
像307和197这些确切的、实际的数就是准确数。
像500这一类与实际数量接近的数就是近似数。
描述数据时,有时根据实际情况不需要特别准确,就可以用接近的数来表示。
学习任务一
阅读与理解
03
任务一
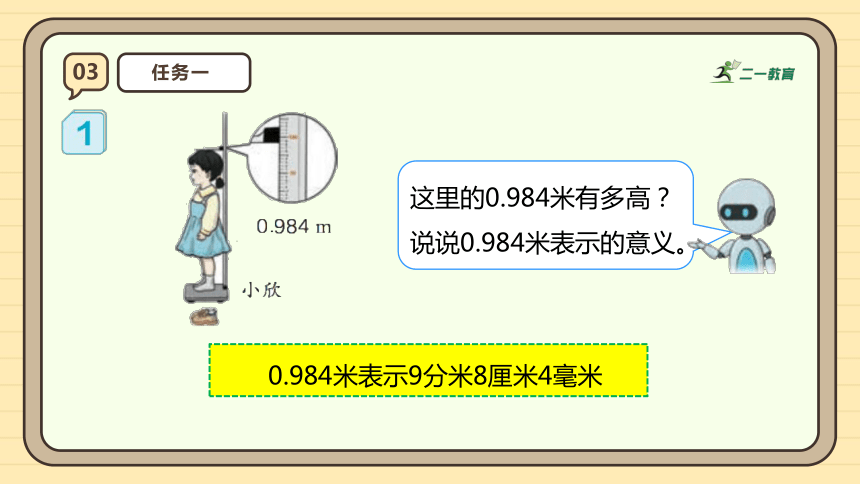
这里的0.984米有多高?说说0.984米表示的意义。
0.984米表示9分米8厘米4毫米
03
任务一
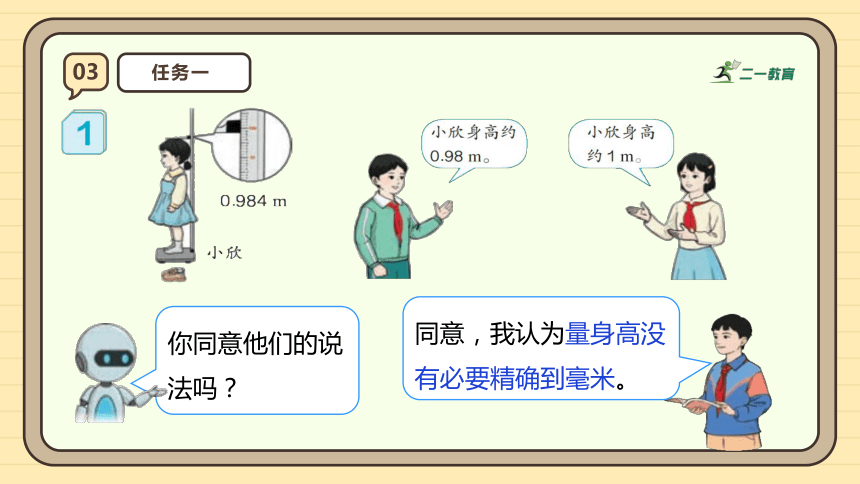
你同意他们的说法吗?
同意,我认为量身高没有必要精确到毫米。
03
任务一
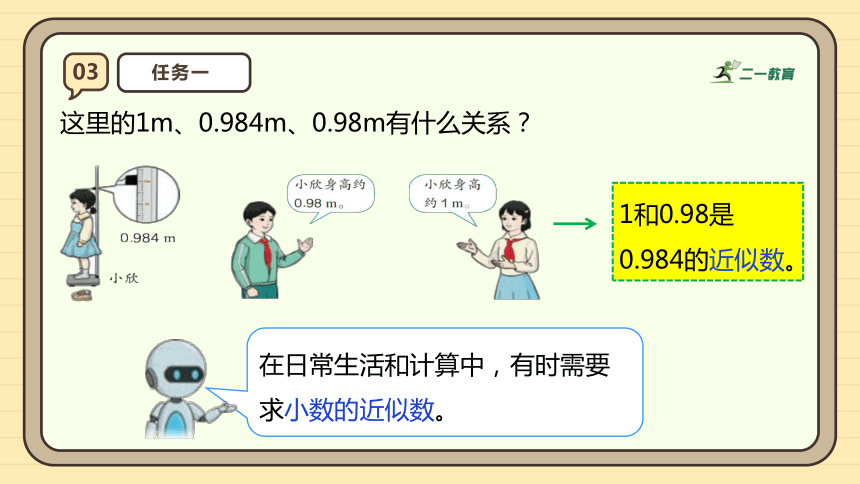
这里的1m、0.984m、0.98m有什么关系?
1和0.98是0.984的近似数。
在日常生活和计算中,有时需要求小数的近似数。
学习任务二
探究求一个小数的近似数的方法
04
任务二
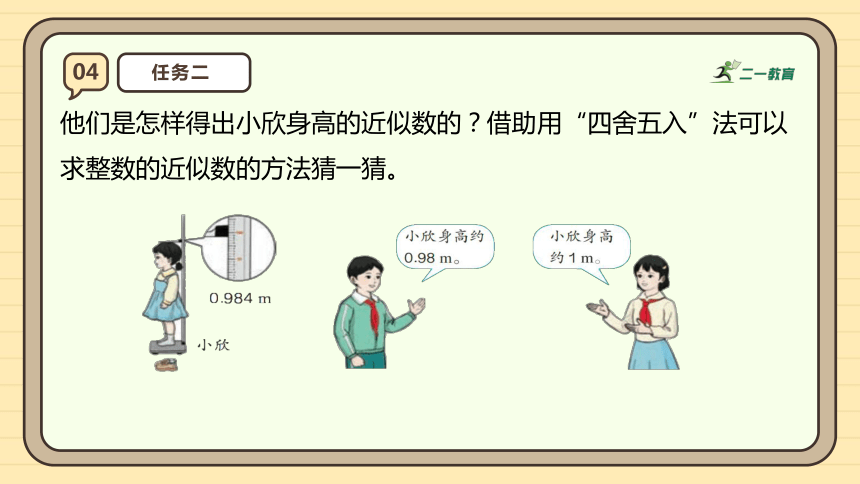
他们是怎样得出小欣身高的近似数的?借助用“四舍五入”法可以求整数的近似数的方法猜一猜。
04
任务二
求一个小数的近似数,同求整数的近似数相似,根据需要用“四舍五入”法保留一定的小数位数。
04
任务二
(1)0.984保留两位小数的近似数是多少?
0 . 9 8 4
如果保留两位小数,就要把千分位上的数省略。
小于5,舍去。
≈ 0.98
保留两位小数就是精确到百分位,需要看千分位上的数,把千分位上的数“四舍五入”。
04
任务二
(2)0.984保留一位小数的近似数是多少?
0 . 9 8 4
如果保留一位小数,就要把百分位上和后面的数省略。
大于5,向前一位进1。
≈ 1.0
保留一位小数就是精确到十分位,需要看百分位上的数,把百分位上的数“四舍五入”。
04
任务二
0 . 9 8 4
大于5,向前一位进1。
≈ 1.0
两次进1一样吗?
第一次是求近似数的方法,满5进1。
第二次9+1=10,满10进1。
两次进1结果一样,但本质不同。
四舍五入的满5进1
十进制计数法的满10进1
04
任务二
保留一位小数1.0,十分位上的“0” 能不能去掉?为什么?
0 . 9 8 4
大于5,向前一位进1。
≈ 1.0
不能去掉的,去掉后就成了1,就不是保留一位小数了。
小
提
示
注意:在表示近似数时,小数末尾的0不能去掉。
04
任务二
学习任务:
把0.984保留到整数的近似数是多少呢?打开课本50页,填一填。如果有困难可以与同伴交流,也可以询问老师。
04
任务二
(3)想一想:0.984≈__________(保留整数)
0 . 9 8 4
保留整数,要把它精确到个位,要看十分位上的数。
大于5,向前一位进1。
≈ 1
保留整数就是精确到个位,需要看十分位上的数,把十分位上的数“四舍五入”。
04
任务二
近似数“1”与近似数“1.0”数值相等,那么它们有什么不同呢?哪一个数更精确一些?
1.0
精确到十分位
1
精确到个位
两个数虽然相等,但精确度不同。
近似数1.0更精确。
04
任务二
求一个数的近似数,保留不同的位数,求得的近似数不同。保留的小数位数越多,这个近似数就越接近准确数,也就更精确。
04
任务二
结合前面求0.984的近似数,你有什么收获?
求近似数时,保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
04
任务二
怎样求一个小数的近似数?
求一个小数的近似数,用“四舍五入”法,精确到哪一位,就要看它的下一位。
05
课堂练习
基础题:
1.判断。
√
×
精确到百分位就是要保留两位小数。
05
课堂练习
基础题:
1.判断。
√
×
1.099和1.081保留一位小数后都是1.1。
05
课堂练习
基础题:
1.判断。
√
×
0.991保留一位小数,省得到的近似数是1.0,末尾的0能省略。
05
课堂练习
基础题:
2.填一填。
保留两位小数 保留一位小数 保留整数
1.063
0.996
2.217
1.06
1.1
1
1.00
1.0
1
2.22
2.2
2
05
作业设计
提高题:
3.《兰亭序》公认最好的摹本是一个长约70cm,宽约25cm的长方形,它的面积约是多少平方米 (保留两位小数)
70×25=1750cm2
=0.175m2
≈0.18m2
答:它的面积约是0.18平方米。
05
课堂练习
拓展题:
4.一个小数的小数部分是两位,当用“四舍五入”法留一位小数后近似值是4.0,这个小数原来最小是多少?最大是多少?
“四舍”得到的4.0最大是4.04。
“五入”得到的4.0最小是3.95。
答:这个小数原来最小是3.95,最大是4.04。
【知识技能类作业】
必做题:
1.按要求填一填。
5.074(保留一位小数)≈_____________
21.363(精确到百分位)≈_____________
2.0476(保留三位小数)≈_____________
6.054(保留一位小数)≈____________
20.0473(精确到百分位)≈____________
06
作业设计
5.1
21.36
2.048
6.1
20.05
06
作业设计
【知识技能类作业】
必做题:
2.每100千克海水含盐3.5千克,1千克这样的海水含盐多少千克?(得数保留两位小数)
3.5÷100=0.035(千克)
≈0.04(千克)
答:1千克这样的海水大约含盐0.04千克。
06
作业设计
【知识技能类作业】
选做题:
1.根据要求在下面的( )里填上适当的数。
(1)2.58 ≈2.58, 里可以填( )。
(2)19. 4≈20, 里最小填( )。
(3)1. ≈2.0,第一个 里一定填( ),第二个□里可以填( )。
1、2、3、4
5
9
5、6、7、8、9
06
课堂练习
【知识技能类作业】
选做题:
2.在一次演讲比赛中,李浩、林龙、陈轩前三名,三人的成绩保留两位小数记录在下面的表格中,如果将他们的成绩保留一位小数, 那么都约等于10.0分,你能确定三人的成绩以及所得的名次吗?填一填。
姓 名 成 绩 名 次
李 浩 9.9 分 第2名
林 龙 . 8分 第( )名
陈 轩 .02分 第( )名
9
9
9
3
10
1
07
课堂小结
通过今天的学习,你有哪些收获?
我会求一个小数的近似数了。
我还知道在表示小数的近似数时,小数末尾的“0”不能去掉。
08
作业布置
【综合实践类作业】
找找生活中的近似数。
09
板书设计
小数的近似数
0.984≈0.98 保留两位小数,精确到百分位
0.984≈1.0 保留一位小数,精确到十分位 “四舍五入“法
0.984≈1 保留整数,精确到个位
在表示小数的近似数时,小数末尾的“0”不能去掉。
https://www.21cnjy.com/recruitment/home/fine
4.10
小数的近似数
(人教版)四年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
结合具体情境理解小数近似数的意义,掌握求小数近似数的方法,会应用“四舍五入”法求小数的近似数,知道精确度的含义。
01
02
经历求小数近似数的过程,通过测量、观察、发现等活动培养推理及概括能力,初步掌握“迁移”和“数形结合”等数学思想方法。
03
感受近似数的实际意义,体会数学与生活的密切联系,激发学习兴趣,培养学生的数感。
02
新知导入
李叔叔在超市买一个电饭煲和一个电饼铛。
电饭煲307元 电饼铛197元
李叔叔大约花了多少钱?估一估,算一算。
02
新知导入
李叔叔在超市买一个电饭煲和一个电饼铛。李叔叔大约花了多少钱?估一估,算一算
把307看作300,把197看作200。
300+200=500(元)
准确数
近似数
02
新知导入
像307和197这些确切的、实际的数就是准确数。
像500这一类与实际数量接近的数就是近似数。
描述数据时,有时根据实际情况不需要特别准确,就可以用接近的数来表示。
学习任务一
阅读与理解
03
任务一
这里的0.984米有多高?说说0.984米表示的意义。
0.984米表示9分米8厘米4毫米
03
任务一
你同意他们的说法吗?
同意,我认为量身高没有必要精确到毫米。
03
任务一
这里的1m、0.984m、0.98m有什么关系?
1和0.98是0.984的近似数。
在日常生活和计算中,有时需要求小数的近似数。
学习任务二
探究求一个小数的近似数的方法
04
任务二
他们是怎样得出小欣身高的近似数的?借助用“四舍五入”法可以求整数的近似数的方法猜一猜。
04
任务二
求一个小数的近似数,同求整数的近似数相似,根据需要用“四舍五入”法保留一定的小数位数。
04
任务二
(1)0.984保留两位小数的近似数是多少?
0 . 9 8 4
如果保留两位小数,就要把千分位上的数省略。
小于5,舍去。
≈ 0.98
保留两位小数就是精确到百分位,需要看千分位上的数,把千分位上的数“四舍五入”。
04
任务二
(2)0.984保留一位小数的近似数是多少?
0 . 9 8 4
如果保留一位小数,就要把百分位上和后面的数省略。
大于5,向前一位进1。
≈ 1.0
保留一位小数就是精确到十分位,需要看百分位上的数,把百分位上的数“四舍五入”。
04
任务二
0 . 9 8 4
大于5,向前一位进1。
≈ 1.0
两次进1一样吗?
第一次是求近似数的方法,满5进1。
第二次9+1=10,满10进1。
两次进1结果一样,但本质不同。
四舍五入的满5进1
十进制计数法的满10进1
04
任务二
保留一位小数1.0,十分位上的“0” 能不能去掉?为什么?
0 . 9 8 4
大于5,向前一位进1。
≈ 1.0
不能去掉的,去掉后就成了1,就不是保留一位小数了。
小
提
示
注意:在表示近似数时,小数末尾的0不能去掉。
04
任务二
学习任务:
把0.984保留到整数的近似数是多少呢?打开课本50页,填一填。如果有困难可以与同伴交流,也可以询问老师。
04
任务二
(3)想一想:0.984≈__________(保留整数)
0 . 9 8 4
保留整数,要把它精确到个位,要看十分位上的数。
大于5,向前一位进1。
≈ 1
保留整数就是精确到个位,需要看十分位上的数,把十分位上的数“四舍五入”。
04
任务二
近似数“1”与近似数“1.0”数值相等,那么它们有什么不同呢?哪一个数更精确一些?
1.0
精确到十分位
1
精确到个位
两个数虽然相等,但精确度不同。
近似数1.0更精确。
04
任务二
求一个数的近似数,保留不同的位数,求得的近似数不同。保留的小数位数越多,这个近似数就越接近准确数,也就更精确。
04
任务二
结合前面求0.984的近似数,你有什么收获?
求近似数时,保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
04
任务二
怎样求一个小数的近似数?
求一个小数的近似数,用“四舍五入”法,精确到哪一位,就要看它的下一位。
05
课堂练习
基础题:
1.判断。
√
×
精确到百分位就是要保留两位小数。
05
课堂练习
基础题:
1.判断。
√
×
1.099和1.081保留一位小数后都是1.1。
05
课堂练习
基础题:
1.判断。
√
×
0.991保留一位小数,省得到的近似数是1.0,末尾的0能省略。
05
课堂练习
基础题:
2.填一填。
保留两位小数 保留一位小数 保留整数
1.063
0.996
2.217
1.06
1.1
1
1.00
1.0
1
2.22
2.2
2
05
作业设计
提高题:
3.《兰亭序》公认最好的摹本是一个长约70cm,宽约25cm的长方形,它的面积约是多少平方米 (保留两位小数)
70×25=1750cm2
=0.175m2
≈0.18m2
答:它的面积约是0.18平方米。
05
课堂练习
拓展题:
4.一个小数的小数部分是两位,当用“四舍五入”法留一位小数后近似值是4.0,这个小数原来最小是多少?最大是多少?
“四舍”得到的4.0最大是4.04。
“五入”得到的4.0最小是3.95。
答:这个小数原来最小是3.95,最大是4.04。
【知识技能类作业】
必做题:
1.按要求填一填。
5.074(保留一位小数)≈_____________
21.363(精确到百分位)≈_____________
2.0476(保留三位小数)≈_____________
6.054(保留一位小数)≈____________
20.0473(精确到百分位)≈____________
06
作业设计
5.1
21.36
2.048
6.1
20.05
06
作业设计
【知识技能类作业】
必做题:
2.每100千克海水含盐3.5千克,1千克这样的海水含盐多少千克?(得数保留两位小数)
3.5÷100=0.035(千克)
≈0.04(千克)
答:1千克这样的海水大约含盐0.04千克。
06
作业设计
【知识技能类作业】
选做题:
1.根据要求在下面的( )里填上适当的数。
(1)2.58 ≈2.58, 里可以填( )。
(2)19. 4≈20, 里最小填( )。
(3)1. ≈2.0,第一个 里一定填( ),第二个□里可以填( )。
1、2、3、4
5
9
5、6、7、8、9
06
课堂练习
【知识技能类作业】
选做题:
2.在一次演讲比赛中,李浩、林龙、陈轩前三名,三人的成绩保留两位小数记录在下面的表格中,如果将他们的成绩保留一位小数, 那么都约等于10.0分,你能确定三人的成绩以及所得的名次吗?填一填。
姓 名 成 绩 名 次
李 浩 9.9 分 第2名
林 龙 . 8分 第( )名
陈 轩 .02分 第( )名
9
9
9
3
10
1
07
课堂小结
通过今天的学习,你有哪些收获?
我会求一个小数的近似数了。
我还知道在表示小数的近似数时,小数末尾的“0”不能去掉。
08
作业布置
【综合实践类作业】
找找生活中的近似数。
09
板书设计
小数的近似数
0.984≈0.98 保留两位小数,精确到百分位
0.984≈1.0 保留一位小数,精确到十分位 “四舍五入“法
0.984≈1 保留整数,精确到个位
在表示小数的近似数时,小数末尾的“0”不能去掉。
https://www.21cnjy.com/recruitment/home/fine
