沪科版七下(2024版)8.2.1 单项式与单项式相乘
文档属性
| 名称 | 沪科版七下(2024版)8.2.1 单项式与单项式相乘 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第8章 整式乘法与因式分解
8.2.1 单项式与单项式相乘
01
学习目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
学习目标
理解和掌握单项式与单项式相乘的运算法则,能够正确进行单项式乘法的计算。
01
通过观察和比较,探索单项式乘法的运算规律,提升观察能力和归纳能力。
02
通过具体的计算过程,提高运算能力和解决问题的能力。
03
02
新知导入
光的速度大约是3×105 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球,1年以3.15×107 s计算,试问地球与这颗恒星的距离约为多少千米?
路程=速度×时间
地球与比邻星的距离应是(3×105)×(4×3.15×107)
思考:这个式子应如何计算呢?
02
新知导入
(3×105)×(4×3.15×107)
=(4×3×3.15)×(105×107)
=37.8×1012
=3.78×1013(km).
所以,地球与这颗恒星的距离约为3.78×1013km.
思考:该运算运用了什么性质?
乘法交换律、乘法结合律
同底数幂的乘法
科学计数法
03
新知探究
如果把上面算式中的数字换成字母,例如bc5·abc7,该如何计算呢?
bc5·abc7
=a·b·b·c5·c7
=a·(b·b) ·(c5·c7)
=a·b2·c12
=ab2c12
乘法交换律
乘法结合律
同底数幂的乘法
“·”可省略
交流
完成下面计算:
4x2y·3xy2=(4×3)·(x ·_____)·(y·_____)=_________;
5abc·(-3ab)=[5×(-3)]·(a·_____)·(b·_____)·c =_________.
y2
x
12x3y2
b
a
-15a2b2c
从以上的计算过程中,你能归纳出单项式乘法的法则吗?
单项式乘法法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
03
新知探究
单项式乘单项式的一般步骤:
1.确定系数:积的系数等于各系数的积
2.确定相同的字母:同底数幂相乘,底数不变,指数相加
3.确定单独字母:只在一个单项式里含有的字母,连同它的指数一起作为积的因式
03
新知探究
计算:(1)abc)(ab); (2)(3a) ·(-5ab ).
例1
解:(1)abc)(ab)
=(-4×)·a2b2c
=-2a2b2c
注意:单项式与单项式相乘,凡在单项式里出现的字母,在结果中应全有,不能漏掉.
03
新知探究
计算:(1)abc)(ab); (2)(3a) ·(-5ab ).
例1
解:(2)(3a) ·(-5ab )
=27a ·(-5ab )
=-135a4b2.
注意:有乘方先算乘方,再算乘法。
03
新知探究
例2 2021年5月15日7时18分,天问一号探测器着陆火星,迈出了我国星际探测征程的重要一步,也使我国成为第二个成功登陆火星的国家.天问一号从地球飞行进入环火轨道的里程相当于绕地球赤道1.18×104圈,它的这一飞行里程约为多少千米?(地球半径r约6.4×10 km,π取 3.14)
解:1.18×104×2πr
≈1.18×104×2×3.14×6.4×10
≈4.74×108(km)
答:它的这一飞行里程约为4.74×108 km.
04
课堂练习
【知识技能类作业】必做题:
1.计算的结果可以用科学记数法表示为( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.若单项式和的积为,则的值为( )
A.2 B.30 C. D.15
D
C
D
04
课堂练习
【知识技能类作业】选做题:
4.长方形的长为,宽为,则它的面积为 .
5.若一个三角形的底边长为,这条底边上的高为,则它的面积为 .
6.已知有理数满足,则 .
-4
04
课堂练习
【综合拓展类作业】
7.计算:(1);
(2);
(3).
(1)解:
;
04
课堂练习
(2)解:
;
(3)解:
.
05
课堂小结
单项式乘法法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式乘单项式的一般步骤:
1.确定系数:积的系数等于各系数的积
2.确定相同的字母:同底数幂相乘,底数不变,指数相加
3.确定单独字母:只在一个单项式里含有的字母,连同它的指数一起作为积的因式
06
作业布置
【知识技能类作业】
1.计算的结果是( )
A. B. C. D.
2.若,则( )
A. B.
C. D.
B
C
06
作业布置
【知识技能类作业】
3.下列关于单项式乘法的说法中,不正确的是( )
A.几个单项式的积仍是单项式
B.几个单项式相乘,有一个因式为0,积一定为0
C.几个符号相同的单项式相乘,积为正数
D.几个不为0的单项式的积的次数不可能比各个单项式的次数低
C
06
作业布置
【综合拓展类作业】
4.先化简,再求值:,其中.
解:
,
当时,原式.
07
板书设计
单项式乘法法则:
单项式乘单项式的一般步骤:
1.确定系数
2.确定相同的字母
3.确定单独字母
8.2.1 单项式与单项式相乘
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第8章 整式乘法与因式分解
8.2.1 单项式与单项式相乘
01
学习目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
学习目标
理解和掌握单项式与单项式相乘的运算法则,能够正确进行单项式乘法的计算。
01
通过观察和比较,探索单项式乘法的运算规律,提升观察能力和归纳能力。
02
通过具体的计算过程,提高运算能力和解决问题的能力。
03
02
新知导入
光的速度大约是3×105 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球,1年以3.15×107 s计算,试问地球与这颗恒星的距离约为多少千米?
路程=速度×时间
地球与比邻星的距离应是(3×105)×(4×3.15×107)
思考:这个式子应如何计算呢?
02
新知导入
(3×105)×(4×3.15×107)
=(4×3×3.15)×(105×107)
=37.8×1012
=3.78×1013(km).
所以,地球与这颗恒星的距离约为3.78×1013km.
思考:该运算运用了什么性质?
乘法交换律、乘法结合律
同底数幂的乘法
科学计数法
03
新知探究
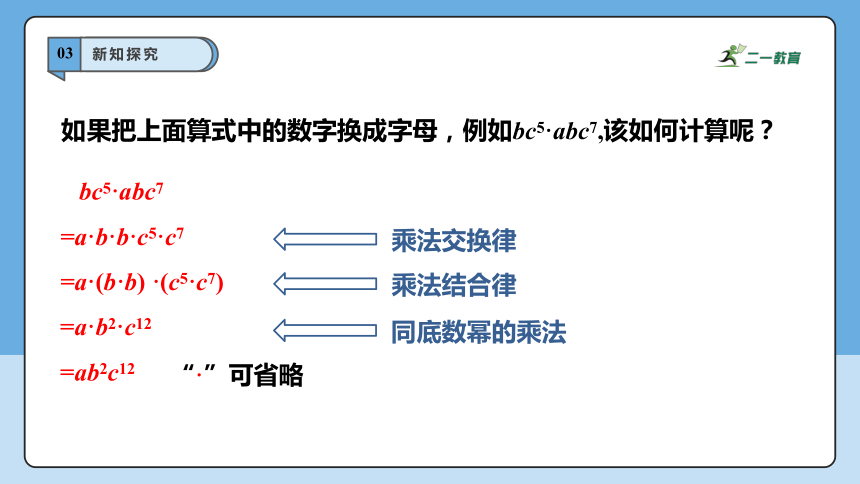
如果把上面算式中的数字换成字母,例如bc5·abc7,该如何计算呢?
bc5·abc7
=a·b·b·c5·c7
=a·(b·b) ·(c5·c7)
=a·b2·c12
=ab2c12
乘法交换律
乘法结合律
同底数幂的乘法
“·”可省略
交流
完成下面计算:
4x2y·3xy2=(4×3)·(x ·_____)·(y·_____)=_________;
5abc·(-3ab)=[5×(-3)]·(a·_____)·(b·_____)·c =_________.
y2
x
12x3y2
b
a
-15a2b2c
从以上的计算过程中,你能归纳出单项式乘法的法则吗?
单项式乘法法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
03
新知探究
单项式乘单项式的一般步骤:
1.确定系数:积的系数等于各系数的积
2.确定相同的字母:同底数幂相乘,底数不变,指数相加
3.确定单独字母:只在一个单项式里含有的字母,连同它的指数一起作为积的因式
03
新知探究
计算:(1)abc)(ab); (2)(3a) ·(-5ab ).
例1
解:(1)abc)(ab)
=(-4×)·a2b2c
=-2a2b2c
注意:单项式与单项式相乘,凡在单项式里出现的字母,在结果中应全有,不能漏掉.
03
新知探究
计算:(1)abc)(ab); (2)(3a) ·(-5ab ).
例1
解:(2)(3a) ·(-5ab )
=27a ·(-5ab )
=-135a4b2.
注意:有乘方先算乘方,再算乘法。
03
新知探究
例2 2021年5月15日7时18分,天问一号探测器着陆火星,迈出了我国星际探测征程的重要一步,也使我国成为第二个成功登陆火星的国家.天问一号从地球飞行进入环火轨道的里程相当于绕地球赤道1.18×104圈,它的这一飞行里程约为多少千米?(地球半径r约6.4×10 km,π取 3.14)
解:1.18×104×2πr
≈1.18×104×2×3.14×6.4×10
≈4.74×108(km)
答:它的这一飞行里程约为4.74×108 km.
04
课堂练习
【知识技能类作业】必做题:
1.计算的结果可以用科学记数法表示为( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.若单项式和的积为,则的值为( )
A.2 B.30 C. D.15
D
C
D
04
课堂练习
【知识技能类作业】选做题:
4.长方形的长为,宽为,则它的面积为 .
5.若一个三角形的底边长为,这条底边上的高为,则它的面积为 .
6.已知有理数满足,则 .
-4
04
课堂练习
【综合拓展类作业】
7.计算:(1);
(2);
(3).
(1)解:
;
04
课堂练习
(2)解:
;
(3)解:
.
05
课堂小结
单项式乘法法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式乘单项式的一般步骤:
1.确定系数:积的系数等于各系数的积
2.确定相同的字母:同底数幂相乘,底数不变,指数相加
3.确定单独字母:只在一个单项式里含有的字母,连同它的指数一起作为积的因式
06
作业布置
【知识技能类作业】
1.计算的结果是( )
A. B. C. D.
2.若,则( )
A. B.
C. D.
B
C
06
作业布置
【知识技能类作业】
3.下列关于单项式乘法的说法中,不正确的是( )
A.几个单项式的积仍是单项式
B.几个单项式相乘,有一个因式为0,积一定为0
C.几个符号相同的单项式相乘,积为正数
D.几个不为0的单项式的积的次数不可能比各个单项式的次数低
C
06
作业布置
【综合拓展类作业】
4.先化简,再求值:,其中.
解:
,
当时,原式.
07
板书设计
单项式乘法法则:
单项式乘单项式的一般步骤:
1.确定系数
2.确定相同的字母
3.确定单独字母
8.2.1 单项式与单项式相乘
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
