4.2 正比例和反比例 第二课时 反比例 同步练习 2024--2025学年小学数学人教版六年级下册
文档属性
| 名称 | 4.2 正比例和反比例 第二课时 反比例 同步练习 2024--2025学年小学数学人教版六年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.2 正比例和反比例 第二课时 反比例 同步练习
2024--2025学年小学数学人教版六年级下册
一、选择题
1.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.15a=9b B.-=0 C.8a= D.=a
2.如果xy=2k+3,当k为大于0的一个常数时,x和y( )。
A.成反比例 B.成正比例 C.不成比例 D.无法判断
3.用四根木条制作一个平行四边形框架,双手将它的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高( )。
A.成正比例关系 B.成反比例关系
C.不成比例 D.不确定
4.下面关于正比例、反比例的说法,正确的有( )个。
①因为直径×圆周率=圆的周长,所以当圆的周长一定时,直径与圆周率成反比例。
②因为爸爸的年龄÷亮亮的年龄=3,所以爸爸的年龄与亮亮的年龄成正比例。
③因为5x-2y=0,所以x与y不成比例。
④上图是甲、乙两车所行路程与时间的关系图,从图中可以看出甲、乙两车的路程与时间都是成正比例关系。
A.1 B.2 C.3 D.4
5.下面关于正比例和反比例的四个说法,正确的有( )。
①圆锥的高一定,它的体积和底面积成正比例关系。
②运动员的跳高成绩和身高不成比例关系。
③三角形的面积一定,它的底和高成反比例关系。
④路程一定,已走的路程和剩下的路程成正比例关系。
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
6.某商场所有物品都打同样的折扣销售。原价200元的衣服,现价140元。如果用a表示原价,b表示现价,用式子表示a和b之间的数量关系是( ),a和b成( )比例关系。
7.填空。
x 27 ?
y 3 9
(1)如果x和y成正比例,“?”处填 。
(2)如果x和y成反比例,“?”处填 。
8.把相同体积的水倒入底面积不同的长方体容器中,变化情况如下表:
底面积/cm2 10 15 20 25 …
水高度/cm 45 30 22.5 18 …
如果长方体容器底面积用S表示,水的高度用h表示,S和h成( )比例;如果底面积30cm2,水高度是( )cm。
9.如果xy=5(x、y均不为0),那么x和y成( )比例关系;如果y=5x(x、y均不为0),那么x和y成( )比例关系。
10.正方形的周长和边长成( )比例;(x、y是均不为0的自然数),k一定时,x和y成( )比例。
11.三个相关联的量,A表示单价,B表示数量,C表示总价。如果A一定,那么B和C成( )比例关系;如果C一定,那么A和B成( )比例关系。
三、判断题
12.长方体的体积一定,它的底面积和高成反比例。( )
13.李老师从家到学校已经走了的路程和剩下的路程成反比例关系。( )
14.如果,那么与不成比例。( )
15.路程一定,已行的千米数和余下的千米数成反比例。( )
四、解答题
16.六年级的同学参加广播体操展演,如果每行站12人,可以站8行;如果每行站16人,可以站几行?
(1)题目中相关联的两个量是( )和( )。
(2)根据“六年级的同学参加广播体操展演”可知,( )一定,所以每行站的人数和行数成( )比例关系。
(3)用比例的知识解答,解:设可以站x行,列出比例式为:( )。
17.看图回答问题。
(1)香蕉的总价和购买的质量成正比例吗?苹果呢?
(2)从图像上看,苹果和香蕉哪种水果贵一些?你是怎么看出来的?
(3)利用图像估计一下,苹果、香蕉各买2.5千克的总价分别是多少元?
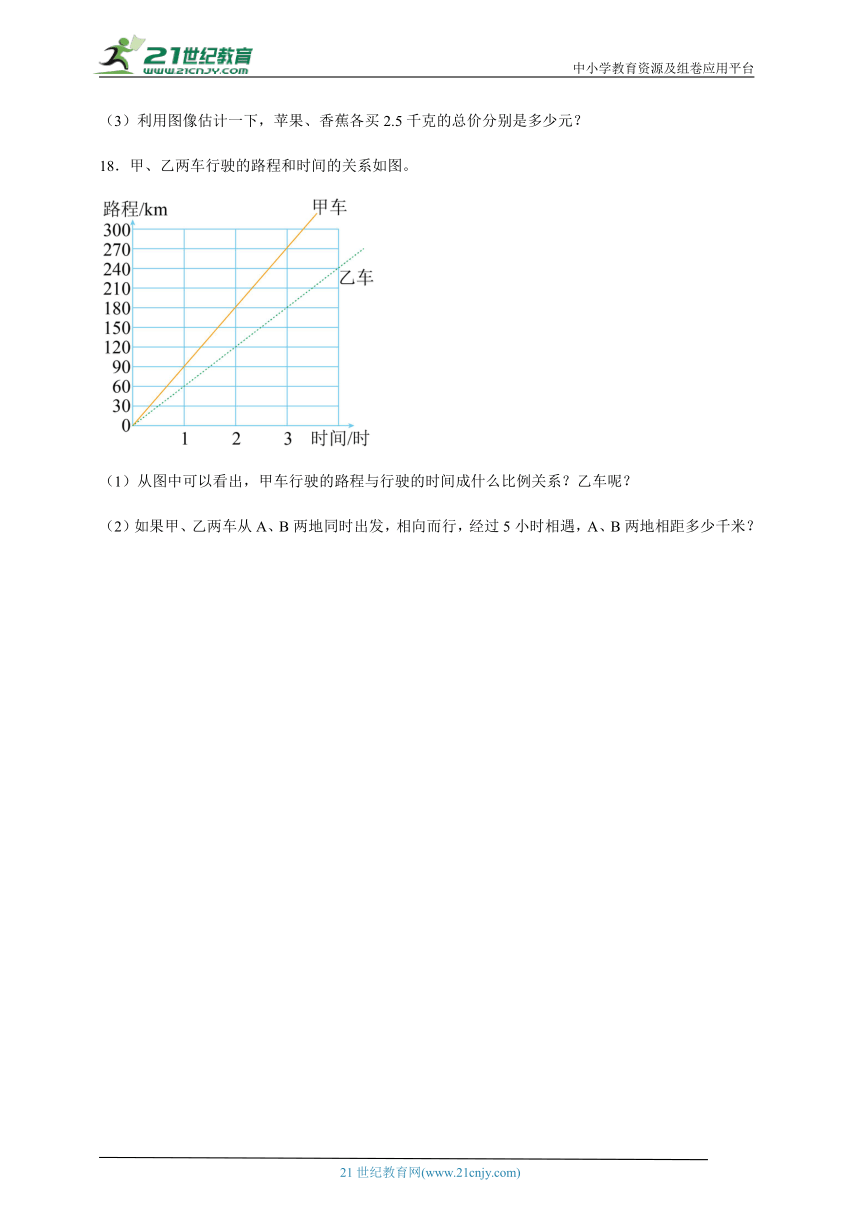
18.甲、乙两车行驶的路程和时间的关系如图。
(1)从图中可以看出,甲车行驶的路程与行驶的时间成什么比例关系?乙车呢?
(2)如果甲、乙两车从A、B两地同时出发,相向而行,经过5小时相遇,A、B两地相距多少千米?
参考答案
1.B
A.由15a=9b可得:=(一定),比值一定,则a和b成正比例;
B.由-=0可得:=,即ab=15×3=45(一定),积一定,则a和b成反比例;
C.由8a=可得:8a=b,即a∶b=∶8=÷8=×=(一定),比值一定,则a和b成正比例;
D.由=a可得:b-7=14a,即b-14a=7,既不是比值一定,也不是乘积一定,则a和b不成比例。
故答案为:B
2.A
判断x和y成不成比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果比值一定,就成正比例,如果乘积一定,就成反比例,如果是其他量一定或乘积、比值不一定,就不成比例。
已知方程:xy=2k+3,k为大于0的常数,若x增大,为了保持等式成立,y应变小,因为xy乘积为常数,所以如果xy=2k+3,当k为大于0的一个常数时,x和y成反比例。
故答案为:A
3.A
判断两个相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
因为在这个变化过程中平行四边形的底不变,根据平行四边形的面积÷高=底(一定),它们的比值不变,所以平行四边形的面积和高成正比例。
4.A
x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
①虽然直径×圆周率=圆的周长,但是圆周率是个定量,因此当圆的周长一定时,直径与圆周率不成比例关系,原说法错误;
②年龄差永不变,年龄之间的倍数关系会随着年龄的变化而变化,所以爸爸的年龄与亮亮的年龄不成比例关系,原说法错误;
③根据5x-2y=0,两边同时+2y,可得5x=2y,两边同时÷y,再÷5,可得x÷y=0.4,x与y成正比例关系,原说法错误;
④正比例图像是一条经过原点的直线,看图可知甲、乙两车的路程与时间都是成正比例关系,原说法正确。
正确的有1个。
故答案为:A
5.A
①圆锥的体积÷圆锥的底面积=高×3(一定),商一定,它的体积和底面积成正比例关系;
②运动员的跳高成绩和身高不成比例关系是正确的;
③三角形的高×底=2×三角形的面积(一定),乘积一定,它的高和底成反比例关系;
④已走的路程+剩下的路程=总路程(一定),和一定,已经走的路程和剩下的路程不成比例。
所以正确的有:①②③。
故答案为:A
6. a×70%=b 正
用现价÷原价×100%,求出打几折;把原价看作单位“1”,用原价×折扣=现价,据此用式子表示a和b之间的数量关系。判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
140÷200×100%
=0.7×100%
=70%
70%就是七折。
a×70%=b
=70%(一定),则a和b成正比例。
某商场所有物品都打同样的折扣销售。原价200元的衣服,现价140元。如果用a表示原价,b表示现价,用式子表示a和b之间的数量关系是a×70%=b,a和b成正比例关系。
7.(1)81
(2)9
(1)两个相关的量,如果它们的比值(商)一定,它们成正比例关系;
(2)两个相关的量,如果它们的乘积一定,它们成反比例关系;据此解答。
(1)如果x和y成正比例,x和y的比值一定。
27∶3=9,所以,x=9×9=81
x 27 81
y 3 9
即如果x和y成正比例,“?”处填81。
(2)如果x和y成反比例,x和y的乘积一定。
27×3=81,所以,x=81÷9=9
x 27 9
y 3 9
即如果x和y成反比例,“?”处填9。
8. 反 15
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。
先从表格中任意选取一组数据,根据V=Sh求出水的体积,再根据h=V÷S,求出底面积是30cm2时水的高度。
V=Sh,体积一定,即乘积一定,则底面积S与高h成反比例;
10×45÷30
=450÷30
=15(cm)
如果长方体容器底面积用S表示,水的高度用h表示,S和h成反比例;如果底面积30cm2,水高度是15cm。
9. 反 正
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
如果xy=5(x、y均不为0),那么x和y成反比例关系;如果y=5x(x、y均不为0),两边同时÷x,可得y÷x=5,那么x和y成正比例关系。
10. 正 反
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
正方形的周长÷边长=4(一定),所以正方形的周长和边长成正比例;
(x、y是均不为7的自然数),那么xy=k+7(一定),所以x和y成反比例。
11. 正 反
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
根据总价÷数量=单价,如果A一定,那么B和C成正比例关系;根据单价×数量=总价,如果C一定,那么A和B成反比例关系。
12.√
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
长方体底面积×高=体积,长方体的体积一定,它的底面积和高成反比例,说法正确。
故答案为:√
13.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
已经走了的路程+剩下的路程=总路程(一定),是和一定,所以李老师从家到学校已经走了的路程和剩下的路程不成比例关系。所以原题说法错误。
故答案为:×
14.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
因为2y=x×
x∶y=2∶
x∶y=2×5
x∶y=10
所以x∶y=10(一定),x和y成正比例。
如果2y=x×,那么x和y成正比例。
原题干说法错误。
故答案为:×
15.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答即可。
已行的千米数+余下的千米数=路程,所以已行的千米数和余下的千米数不成比例,本题说法错误。
故答案为:×
16.(1) 每行站的人数 行数
(2) 总人数 反
(3)16x=12×8
(1)根据题意,题目中相关联的两个量是每行站的人数和行数;
(2)根据“六年级的同学参加广播体操展演”可知,总人数一定,所以每行站的人数和行数成反比例关系。
(3)解:设可以站x行。
16x=12×8
16x=96
16x÷16=96÷16
x=6
答:可以站6行。
17.(1)香蕉的总价和购买的质量成正比例;苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;由图像可知,1千克香蕉8元,1千克苹果4元,所以香蕉贵一些。
(3)苹果总价10元;香蕉总价20元。
(1)香蕉:(元)
(元)
(元)
香蕉的单价为每千克8元(一定),所以香蕉的总价和购买的质量成正比例。
苹果:(元)
(元)
(元)
苹果的单价为每千克4元(一定),所以苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;观察图像可知,1千克苹果4元,1千克香蕉8元,所以香蕉贵一些。(合理即可,答案不唯一)
(3)苹果:(元)
香蕉:(元)
答:2.5千克苹果的总价为10元,2.5千克香蕉的总价为20元。
18.(1)甲车成正比例关系;乙车成正比例关系
(2)750千米
(1)答:从图中可以看出,甲车行驶的路程与行驶的时间成正比例关系,乙车行驶的路程与行驶的时间成正比例关系。
(2)(90+60)×5
=150×5
=750(千米)
答:A、B两地相距750千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.2 正比例和反比例 第二课时 反比例 同步练习
2024--2025学年小学数学人教版六年级下册
一、选择题
1.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.15a=9b B.-=0 C.8a= D.=a
2.如果xy=2k+3,当k为大于0的一个常数时,x和y( )。
A.成反比例 B.成正比例 C.不成比例 D.无法判断
3.用四根木条制作一个平行四边形框架,双手将它的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高( )。
A.成正比例关系 B.成反比例关系
C.不成比例 D.不确定
4.下面关于正比例、反比例的说法,正确的有( )个。
①因为直径×圆周率=圆的周长,所以当圆的周长一定时,直径与圆周率成反比例。
②因为爸爸的年龄÷亮亮的年龄=3,所以爸爸的年龄与亮亮的年龄成正比例。
③因为5x-2y=0,所以x与y不成比例。
④上图是甲、乙两车所行路程与时间的关系图,从图中可以看出甲、乙两车的路程与时间都是成正比例关系。
A.1 B.2 C.3 D.4
5.下面关于正比例和反比例的四个说法,正确的有( )。
①圆锥的高一定,它的体积和底面积成正比例关系。
②运动员的跳高成绩和身高不成比例关系。
③三角形的面积一定,它的底和高成反比例关系。
④路程一定,已走的路程和剩下的路程成正比例关系。
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
6.某商场所有物品都打同样的折扣销售。原价200元的衣服,现价140元。如果用a表示原价,b表示现价,用式子表示a和b之间的数量关系是( ),a和b成( )比例关系。
7.填空。
x 27 ?
y 3 9
(1)如果x和y成正比例,“?”处填 。
(2)如果x和y成反比例,“?”处填 。
8.把相同体积的水倒入底面积不同的长方体容器中,变化情况如下表:
底面积/cm2 10 15 20 25 …
水高度/cm 45 30 22.5 18 …
如果长方体容器底面积用S表示,水的高度用h表示,S和h成( )比例;如果底面积30cm2,水高度是( )cm。
9.如果xy=5(x、y均不为0),那么x和y成( )比例关系;如果y=5x(x、y均不为0),那么x和y成( )比例关系。
10.正方形的周长和边长成( )比例;(x、y是均不为0的自然数),k一定时,x和y成( )比例。
11.三个相关联的量,A表示单价,B表示数量,C表示总价。如果A一定,那么B和C成( )比例关系;如果C一定,那么A和B成( )比例关系。
三、判断题
12.长方体的体积一定,它的底面积和高成反比例。( )
13.李老师从家到学校已经走了的路程和剩下的路程成反比例关系。( )
14.如果,那么与不成比例。( )
15.路程一定,已行的千米数和余下的千米数成反比例。( )
四、解答题
16.六年级的同学参加广播体操展演,如果每行站12人,可以站8行;如果每行站16人,可以站几行?
(1)题目中相关联的两个量是( )和( )。
(2)根据“六年级的同学参加广播体操展演”可知,( )一定,所以每行站的人数和行数成( )比例关系。
(3)用比例的知识解答,解:设可以站x行,列出比例式为:( )。
17.看图回答问题。
(1)香蕉的总价和购买的质量成正比例吗?苹果呢?
(2)从图像上看,苹果和香蕉哪种水果贵一些?你是怎么看出来的?
(3)利用图像估计一下,苹果、香蕉各买2.5千克的总价分别是多少元?
18.甲、乙两车行驶的路程和时间的关系如图。
(1)从图中可以看出,甲车行驶的路程与行驶的时间成什么比例关系?乙车呢?
(2)如果甲、乙两车从A、B两地同时出发,相向而行,经过5小时相遇,A、B两地相距多少千米?
参考答案
1.B
A.由15a=9b可得:=(一定),比值一定,则a和b成正比例;
B.由-=0可得:=,即ab=15×3=45(一定),积一定,则a和b成反比例;
C.由8a=可得:8a=b,即a∶b=∶8=÷8=×=(一定),比值一定,则a和b成正比例;
D.由=a可得:b-7=14a,即b-14a=7,既不是比值一定,也不是乘积一定,则a和b不成比例。
故答案为:B
2.A
判断x和y成不成比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果比值一定,就成正比例,如果乘积一定,就成反比例,如果是其他量一定或乘积、比值不一定,就不成比例。
已知方程:xy=2k+3,k为大于0的常数,若x增大,为了保持等式成立,y应变小,因为xy乘积为常数,所以如果xy=2k+3,当k为大于0的一个常数时,x和y成反比例。
故答案为:A
3.A
判断两个相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
因为在这个变化过程中平行四边形的底不变,根据平行四边形的面积÷高=底(一定),它们的比值不变,所以平行四边形的面积和高成正比例。
4.A
x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
①虽然直径×圆周率=圆的周长,但是圆周率是个定量,因此当圆的周长一定时,直径与圆周率不成比例关系,原说法错误;
②年龄差永不变,年龄之间的倍数关系会随着年龄的变化而变化,所以爸爸的年龄与亮亮的年龄不成比例关系,原说法错误;
③根据5x-2y=0,两边同时+2y,可得5x=2y,两边同时÷y,再÷5,可得x÷y=0.4,x与y成正比例关系,原说法错误;
④正比例图像是一条经过原点的直线,看图可知甲、乙两车的路程与时间都是成正比例关系,原说法正确。
正确的有1个。
故答案为:A
5.A
①圆锥的体积÷圆锥的底面积=高×3(一定),商一定,它的体积和底面积成正比例关系;
②运动员的跳高成绩和身高不成比例关系是正确的;
③三角形的高×底=2×三角形的面积(一定),乘积一定,它的高和底成反比例关系;
④已走的路程+剩下的路程=总路程(一定),和一定,已经走的路程和剩下的路程不成比例。
所以正确的有:①②③。
故答案为:A
6. a×70%=b 正
用现价÷原价×100%,求出打几折;把原价看作单位“1”,用原价×折扣=现价,据此用式子表示a和b之间的数量关系。判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
140÷200×100%
=0.7×100%
=70%
70%就是七折。
a×70%=b
=70%(一定),则a和b成正比例。
某商场所有物品都打同样的折扣销售。原价200元的衣服,现价140元。如果用a表示原价,b表示现价,用式子表示a和b之间的数量关系是a×70%=b,a和b成正比例关系。
7.(1)81
(2)9
(1)两个相关的量,如果它们的比值(商)一定,它们成正比例关系;
(2)两个相关的量,如果它们的乘积一定,它们成反比例关系;据此解答。
(1)如果x和y成正比例,x和y的比值一定。
27∶3=9,所以,x=9×9=81
x 27 81
y 3 9
即如果x和y成正比例,“?”处填81。
(2)如果x和y成反比例,x和y的乘积一定。
27×3=81,所以,x=81÷9=9
x 27 9
y 3 9
即如果x和y成反比例,“?”处填9。
8. 反 15
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。
先从表格中任意选取一组数据,根据V=Sh求出水的体积,再根据h=V÷S,求出底面积是30cm2时水的高度。
V=Sh,体积一定,即乘积一定,则底面积S与高h成反比例;
10×45÷30
=450÷30
=15(cm)
如果长方体容器底面积用S表示,水的高度用h表示,S和h成反比例;如果底面积30cm2,水高度是15cm。
9. 反 正
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
如果xy=5(x、y均不为0),那么x和y成反比例关系;如果y=5x(x、y均不为0),两边同时÷x,可得y÷x=5,那么x和y成正比例关系。
10. 正 反
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
正方形的周长÷边长=4(一定),所以正方形的周长和边长成正比例;
(x、y是均不为7的自然数),那么xy=k+7(一定),所以x和y成反比例。
11. 正 反
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
根据总价÷数量=单价,如果A一定,那么B和C成正比例关系;根据单价×数量=总价,如果C一定,那么A和B成反比例关系。
12.√
两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
长方体底面积×高=体积,长方体的体积一定,它的底面积和高成反比例,说法正确。
故答案为:√
13.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
已经走了的路程+剩下的路程=总路程(一定),是和一定,所以李老师从家到学校已经走了的路程和剩下的路程不成比例关系。所以原题说法错误。
故答案为:×
14.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
因为2y=x×
x∶y=2∶
x∶y=2×5
x∶y=10
所以x∶y=10(一定),x和y成正比例。
如果2y=x×,那么x和y成正比例。
原题干说法错误。
故答案为:×
15.×
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答即可。
已行的千米数+余下的千米数=路程,所以已行的千米数和余下的千米数不成比例,本题说法错误。
故答案为:×
16.(1) 每行站的人数 行数
(2) 总人数 反
(3)16x=12×8
(1)根据题意,题目中相关联的两个量是每行站的人数和行数;
(2)根据“六年级的同学参加广播体操展演”可知,总人数一定,所以每行站的人数和行数成反比例关系。
(3)解:设可以站x行。
16x=12×8
16x=96
16x÷16=96÷16
x=6
答:可以站6行。
17.(1)香蕉的总价和购买的质量成正比例;苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;由图像可知,1千克香蕉8元,1千克苹果4元,所以香蕉贵一些。
(3)苹果总价10元;香蕉总价20元。
(1)香蕉:(元)
(元)
(元)
香蕉的单价为每千克8元(一定),所以香蕉的总价和购买的质量成正比例。
苹果:(元)
(元)
(元)
苹果的单价为每千克4元(一定),所以苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;观察图像可知,1千克苹果4元,1千克香蕉8元,所以香蕉贵一些。(合理即可,答案不唯一)
(3)苹果:(元)
香蕉:(元)
答:2.5千克苹果的总价为10元,2.5千克香蕉的总价为20元。
18.(1)甲车成正比例关系;乙车成正比例关系
(2)750千米
(1)答:从图中可以看出,甲车行驶的路程与行驶的时间成正比例关系,乙车行驶的路程与行驶的时间成正比例关系。
(2)(90+60)×5
=150×5
=750(千米)
答:A、B两地相距750千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
