2.1多边形 第二课时 教案(表格式)湘教版(2024)数学八年级下册
文档属性
| 名称 | 2.1多边形 第二课时 教案(表格式)湘教版(2024)数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 60.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 19:57:59 | ||
图片预览

文档简介
八 年级 数学 教案
课 题 2.1多边形 课 型 新授课
课 时 第二课时 设计者 年 级 八年级
教材分析 本节课是在学生学习了多边形的内角和,知道多边形的边数会求多边形内角和的基础上,来学习外角和的概念.它不仅是对前面所学知识的综合应用,也为后面学习其他几何图形的性质和运算打下基础.
教 学 目 标 1.了解多边形的外角定义,并能准确找出多边形的外角. 2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题. 3.经历探索多边形的外角和公式的过程,进一步发展合情推理意识和主动探究的习惯,体会数学与现实生活的紧密联系,发展说理和简单推理的意识及能力. 4.培养学生主动探索的习惯.
教学重点 经历探索多边形的内角和与外角和公式的过程.
教学难点 推导多边形的内角和与外角和公式,灵活运用公式解决简单的实际问题。
教具准备 课件,直尺
教学方法 阅读、练习、讨论与讲授相结合。
教学过程设计
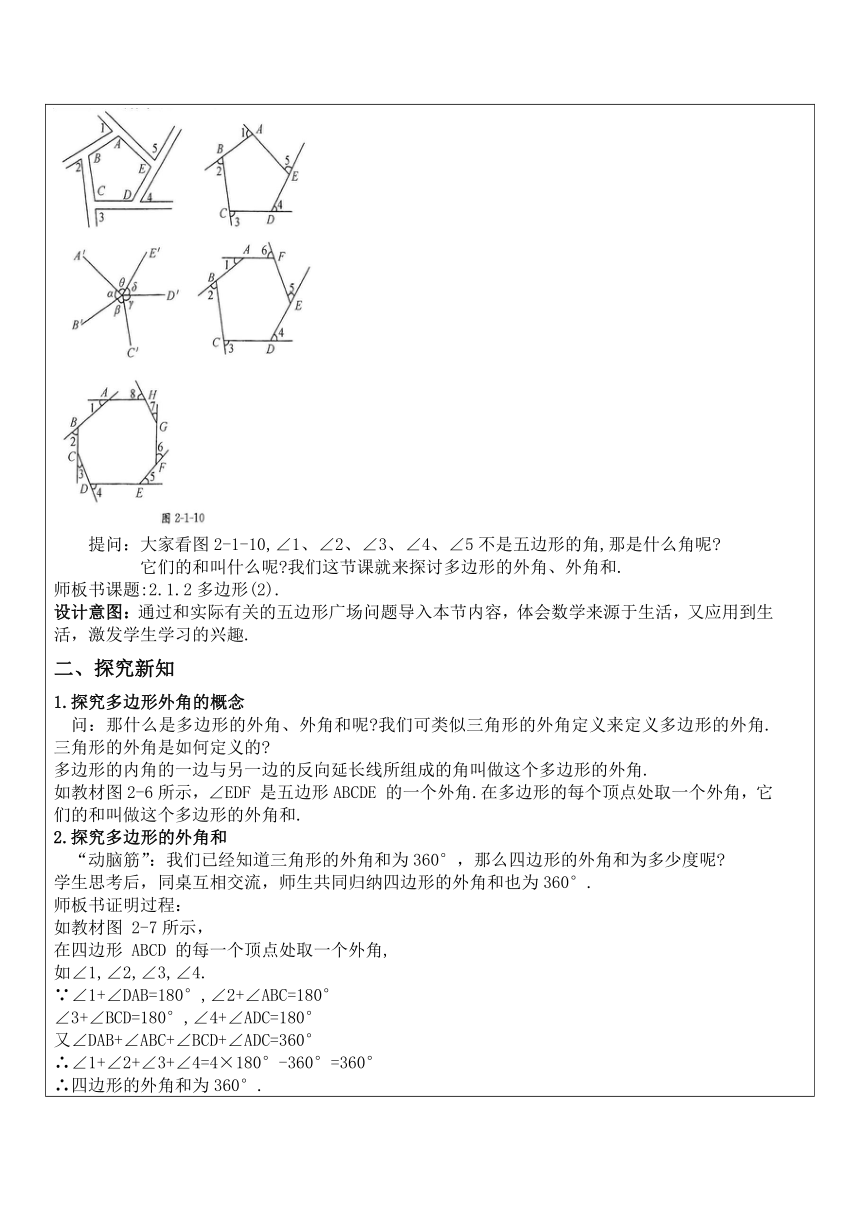
一、旧知导入 教师用多媒体课件展示如下内容,如图2-1-10: 小明沿一个五边形广场周围的小跑,按逆时针方向跑步. (1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角 (2)他每跑完一圈,身体转过的角度之和是多少 (3)在上图2-1-10中,你能求出∠1+∠2+∠3+∠4+∠5吗 你是怎样得到的 提问:大家看图2-1-10,∠1、∠2、∠3、∠4、∠5不是五边形的角,那是什么角呢 它们的和叫什么呢 我们这节课就来探讨多边形的外角、外角和. 师板书课题:2.1.2多边形(2). 设计意图:通过和实际有关的五边形广场问题导入本节内容,体会数学来源于生活,又应用到生活,激发学生学习的兴趣. 二、探究新知 1.探究多边形外角的概念 问:那什么是多边形的外角、外角和呢 我们可类似三角形的外角定义来定义多边形的外角.三角形的外角是如何定义的 多边形的内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 如教材图2-6所示,∠EDF 是五边形ABCDE 的一个外角.在多边形的每个顶点处取一个外角,它们的和叫做这个多边形的外角和. 2.探究多边形的外角和 “动脑筋”:我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢 学生思考后,同桌互相交流,师生共同归纳四边形的外角和也为360°. 师板书证明过程: 如教材图 2-7所示, 在四边形 ABCD 的每一个顶点处取一个外角, 如∠1,∠2,∠3,∠4. ∵∠1+∠DAB=180°,∠2+∠ABC=180° ∠3+∠BCD=180°,∠4+∠ADC=180° 又∠DAB+∠ABC+∠BCD+∠ADC=360° ∴∠1+∠2+∠3+∠4=4×180°-360°=360° ∴四边形的外角和为360°. “探究”三角形的外角和是360°,四边形的外角和是 360°,n边形(n为不小于3的任意整数)的外角和都是360°吗 n边形的外角和与边数有关系吗 提问:类似于求四边形外角和的思路,在n边形的每一个顶点处取一个外角,其中每一个外角与它相邻的内角之和为多少度 探究四边形的不稳定性 课件展示教材38页的“观察”:三角形具有稳定性,四边形呢?用四根木条钉成如教材的框木框,随意扭转四边形的边,它的形状会发生变化吗? 学生思考后,同桌相互交流,师生共同发现:四边形的边长不变,但是它的形状变了,这说明四边形具有不稳定性 三、例题解析 例2.一个多边形的内角和等于它外角和的5倍,它是几边形 解析:先让学生独立思考.学生的第一反应是多边形的内角和公式为(n—2)·180°,任意多边形的外角和都是360°,大部分学生能根据题意列出方程.教师给予适当的评价,让学生明确多边形内角和、外角和与多边形边数的关系,进而列方程求解. 解:设多边形的边数为 n,则它的内角和为(n-2)·180°,由题意得,(n-2)·180°=360°×5,解得n=12.因此这个多边形是十二边形. 例3.一个多边形的内角和比外角和多540°,它是几边形 解:任何多边形的外角和都是540°,则这个多边形的内角和为900°,设这个多边形的边数为n,则( ,解得n=7.所以它是七边形. 方法小结:任意多边形的外角和都等于360°,它是一个定值,不随边数的变化而变化.熟练掌握内角和公式和外角和定理是解决本题的关键. 课堂小结 通过本节课,你有什么收获? 五、巩固练习 1.下列说法不正确的是( ). 答案:C. A.一个多边形外角的个数与边数相同 B.一个多边形外角和一定是360° C.多边形的外角和一定小于它的内角和 D.多边形外角和是所有外角的和 2.多边形的内角和不可能的是( ). 答案:A. A.810° B.540° C.1800° D.180° 3.内角和等于外角和2倍的多边形是( ). 答案:B. A.五边形 B.六边形 C.七边形 D.八边形 4.若多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( ).答案:B. A.6 B.7 C.8 D.9 5、一个多边形边数增加2,则这个多边形内角增加 ,外角增加 . 【讲评】这个多边形内角和增加2×180=360,内角增加2个,多边形外角和不变,仍然为360°,外角增加2个. 答案:2个 2个
板书设计 2.1多边形 第二课时 (1)多边形外角的定义、多边形外角和定理及其证明. (2)任意多边形的外角和都等于360°,它是一个定值,不随边数的变化而变化.
教学后记:
课 题 2.1多边形 课 型 新授课
课 时 第二课时 设计者 年 级 八年级
教材分析 本节课是在学生学习了多边形的内角和,知道多边形的边数会求多边形内角和的基础上,来学习外角和的概念.它不仅是对前面所学知识的综合应用,也为后面学习其他几何图形的性质和运算打下基础.
教 学 目 标 1.了解多边形的外角定义,并能准确找出多边形的外角. 2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题. 3.经历探索多边形的外角和公式的过程,进一步发展合情推理意识和主动探究的习惯,体会数学与现实生活的紧密联系,发展说理和简单推理的意识及能力. 4.培养学生主动探索的习惯.
教学重点 经历探索多边形的内角和与外角和公式的过程.
教学难点 推导多边形的内角和与外角和公式,灵活运用公式解决简单的实际问题。
教具准备 课件,直尺
教学方法 阅读、练习、讨论与讲授相结合。
教学过程设计
一、旧知导入 教师用多媒体课件展示如下内容,如图2-1-10: 小明沿一个五边形广场周围的小跑,按逆时针方向跑步. (1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角 (2)他每跑完一圈,身体转过的角度之和是多少 (3)在上图2-1-10中,你能求出∠1+∠2+∠3+∠4+∠5吗 你是怎样得到的 提问:大家看图2-1-10,∠1、∠2、∠3、∠4、∠5不是五边形的角,那是什么角呢 它们的和叫什么呢 我们这节课就来探讨多边形的外角、外角和. 师板书课题:2.1.2多边形(2). 设计意图:通过和实际有关的五边形广场问题导入本节内容,体会数学来源于生活,又应用到生活,激发学生学习的兴趣. 二、探究新知 1.探究多边形外角的概念 问:那什么是多边形的外角、外角和呢 我们可类似三角形的外角定义来定义多边形的外角.三角形的外角是如何定义的 多边形的内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 如教材图2-6所示,∠EDF 是五边形ABCDE 的一个外角.在多边形的每个顶点处取一个外角,它们的和叫做这个多边形的外角和. 2.探究多边形的外角和 “动脑筋”:我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢 学生思考后,同桌互相交流,师生共同归纳四边形的外角和也为360°. 师板书证明过程: 如教材图 2-7所示, 在四边形 ABCD 的每一个顶点处取一个外角, 如∠1,∠2,∠3,∠4. ∵∠1+∠DAB=180°,∠2+∠ABC=180° ∠3+∠BCD=180°,∠4+∠ADC=180° 又∠DAB+∠ABC+∠BCD+∠ADC=360° ∴∠1+∠2+∠3+∠4=4×180°-360°=360° ∴四边形的外角和为360°. “探究”三角形的外角和是360°,四边形的外角和是 360°,n边形(n为不小于3的任意整数)的外角和都是360°吗 n边形的外角和与边数有关系吗 提问:类似于求四边形外角和的思路,在n边形的每一个顶点处取一个外角,其中每一个外角与它相邻的内角之和为多少度 探究四边形的不稳定性 课件展示教材38页的“观察”:三角形具有稳定性,四边形呢?用四根木条钉成如教材的框木框,随意扭转四边形的边,它的形状会发生变化吗? 学生思考后,同桌相互交流,师生共同发现:四边形的边长不变,但是它的形状变了,这说明四边形具有不稳定性 三、例题解析 例2.一个多边形的内角和等于它外角和的5倍,它是几边形 解析:先让学生独立思考.学生的第一反应是多边形的内角和公式为(n—2)·180°,任意多边形的外角和都是360°,大部分学生能根据题意列出方程.教师给予适当的评价,让学生明确多边形内角和、外角和与多边形边数的关系,进而列方程求解. 解:设多边形的边数为 n,则它的内角和为(n-2)·180°,由题意得,(n-2)·180°=360°×5,解得n=12.因此这个多边形是十二边形. 例3.一个多边形的内角和比外角和多540°,它是几边形 解:任何多边形的外角和都是540°,则这个多边形的内角和为900°,设这个多边形的边数为n,则( ,解得n=7.所以它是七边形. 方法小结:任意多边形的外角和都等于360°,它是一个定值,不随边数的变化而变化.熟练掌握内角和公式和外角和定理是解决本题的关键. 课堂小结 通过本节课,你有什么收获? 五、巩固练习 1.下列说法不正确的是( ). 答案:C. A.一个多边形外角的个数与边数相同 B.一个多边形外角和一定是360° C.多边形的外角和一定小于它的内角和 D.多边形外角和是所有外角的和 2.多边形的内角和不可能的是( ). 答案:A. A.810° B.540° C.1800° D.180° 3.内角和等于外角和2倍的多边形是( ). 答案:B. A.五边形 B.六边形 C.七边形 D.八边形 4.若多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( ).答案:B. A.6 B.7 C.8 D.9 5、一个多边形边数增加2,则这个多边形内角增加 ,外角增加 . 【讲评】这个多边形内角和增加2×180=360,内角增加2个,多边形外角和不变,仍然为360°,外角增加2个. 答案:2个 2个
板书设计 2.1多边形 第二课时 (1)多边形外角的定义、多边形外角和定理及其证明. (2)任意多边形的外角和都等于360°,它是一个定值,不随边数的变化而变化.
教学后记:
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
