2025年九年级数学中考三轮冲刺练习几何压轴题训练(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习几何压轴题训练(含解析) | 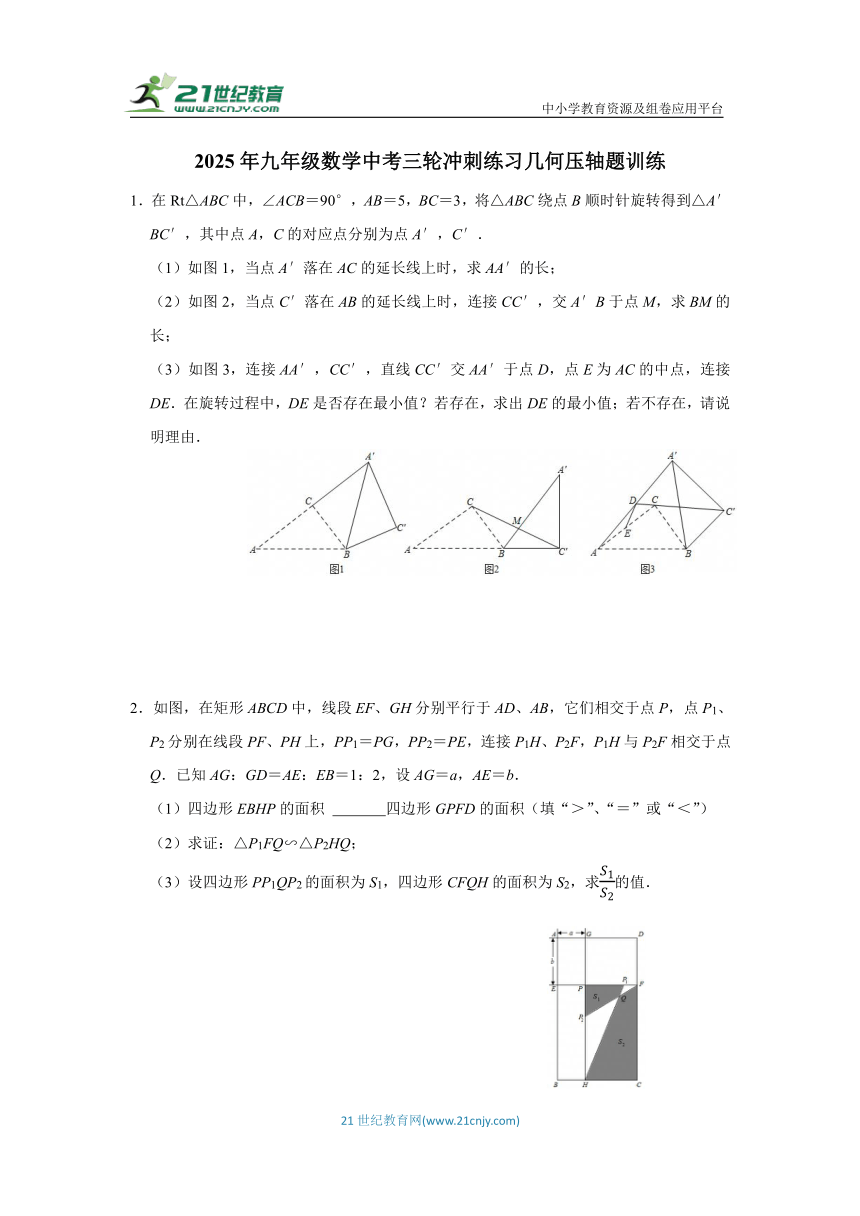 | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 19:33:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习几何压轴题训练
1.在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
2.如图,在矩形ABCD中,线段EF、GH分别平行于AD、AB,它们相交于点P,点P1、P2分别在线段PF、PH上,PP1=PG,PP2=PE,连接P1H、P2F,P1H与P2F相交于点Q.已知AG:GD=AE:EB=1:2,设AG=a,AE=b.
(1)四边形EBHP的面积 四边形GPFD的面积(填“>”、“=”或“<”)
(2)求证:△P1FQ∽△P2HQ;
(3)设四边形PP1QP2的面积为S1,四边形CFQH的面积为S2,求的值.
3.如图,△OAB的顶点坐标分别为O(0,0),A(3,4),B(6,0),动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作MN∥OB分别交AO、AB于点M、N,连接PM、PN.设运动时间为t(秒).
(1)求点M的坐标(用含t的式子表示);
(2)求四边形MNBP面积的最大值或最小值;
(3)是否存在这样的直线l,总能平分四边形MNBP的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;
(4)连接AP,当∠OAP=∠BPN时,求点N到OA的距离.
4.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
5.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: ,∠BDC= °;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系: ;
(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP= .
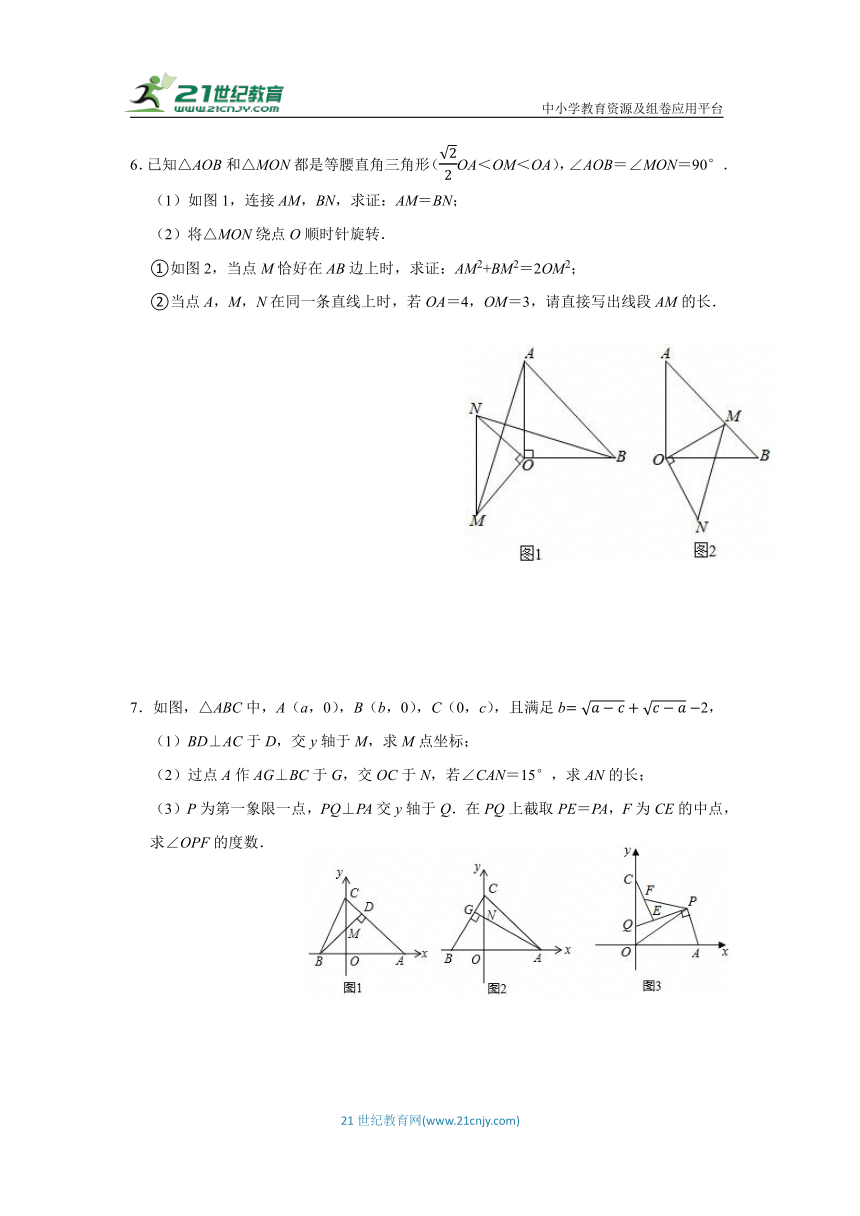
6.已知△AOB和△MON都是等腰直角三角形(OA<OM<OA),∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:AM=BN;
(2)将△MON绕点O顺时针旋转.
①如图2,当点M恰好在AB边上时,求证:AM2+BM2=2OM2;
②当点A,M,N在同一条直线上时,若OA=4,OM=3,请直接写出线段AM的长.
7.如图,△ABC中,A(a,0),B(b,0),C(0,c),且满足b2,
(1)BD⊥AC于D,交y轴于M,求M点坐标;
(2)过点A作AG⊥BC于G,交OC于N,若∠CAN=15°,求AN的长;
(3)P为第一象限一点,PQ⊥PA交y轴于Q.在PQ上截取PE=PA,F为CE的中点,求∠OPF的度数.
8.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠ADC=90°,点E、F分别在边BC、CD上,若∠EAB+∠FAD=∠EAF则线段BE、DF、EF之间的数量关系是 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,若EF=BE+FD,探究∠EAB、∠FAD、∠EAF的之间的数量关系,并说明理由.
(3)如图3,在△ABC中,AB=AC,∠BAC=90°,E是线段AB上一点,CE⊥CF,且CE=CF,过点F作FD⊥FC交CA的延长线于D,过E作EG⊥EC交BC于G,连接DG.若DF=7,EG=1,求DG的长.
9.如图①,△ABC是等边三角形,AB=6.点P从点A出发,沿折线AB﹣BC运动.当点P不与点A重合时,连结AP,以AP为边向其右侧作等腰三角形APQ,使∠AQP=120°,延长AQ交边BC于点D,当点D与点C重合,点P停止运动,连结PD
(1)当点P在边AB上运动时,AD的长为 .
(2)如图②,当点P在边BC上时,求证:.
(3)点P在整个运动过程中,当△PDQ是轴对称图形时,求PD的长.
(4)点P在整个运动过程中,当AB=3BP时,直接写出PD的长
10.如图,Rt△ABC中,∠ACB=90°,D为AB中点,点E在BC边上(点E不与点B,C重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF.
(1)求证:AF2+BE2=EF2
(2)若AC=7,BC=5,EC=1,直接写出线段AF的长.
11.如图,∠ABC=∠ADC=90°,AC与BD相交于点E,∠ABD=∠ADB.
(1)求证:AC垂直平分BD;
(2)过点B作BF∥CD交CA的延长线于F,如果AB=AF;
①求证:△BCD是等边三角形;
②如果G、H分别是线段AC、线段CD上的动点,当GH+AH为最小值时,请确定点H的位置,并思考此时GH与CH有怎样的数量关系.
12.如图,点E在正方形ABCD对角线BD上,连接AE、CE,点F为AB上一点,连接CF,
交BD于点G.连接EF,若AE=EF.
(1)求证:AE=CE;
(2)求∠ECF的度数;
(3)经探究,DE、BG、EG三条线段满足某种数量关系,请直接写出们之间的关系式.
13.如图,在△ABC中,∠BAC=90°,AB=AC,D,E分别为BC上两动点,BD=CE.
(1)如图1,若EH⊥AD于H交AB于K,求证:AE=EK;
(2)如图2,若EF∥AD交AC于F,GF⊥AG,AG=GF,求证:;
(3)如图3,若AB=4,将AE绕点E顺时针旋转90°得EM,N为BM中点,当取得最小值时,请直接写出△ACD的面积.
14.如图,在等腰三角形ABC中,AB=AC,∠ABC=30°,点O为BC的中点,点D是线段OB上的动点(点D不与点O,B重合),将△ABD沿直线AD折叠得到△AED,连接CE.
(1)若AB=AC=5,∠BAD=15°,求CE的长;
(2)若∠BAD=α,则∠AEC= ;
(3)若△ACE是等边三角形,请直接写出的值.
15.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG与DC的延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若CD=8,BE=2,求⊙O的半径长;
(3)若G是的中点,CECF=2,求GF的长.
16.如图1,F为正方形ABCD内一点,点E在边AD上(不与端点A,D重合),BE垂直平分AF交AF于点O,连接CF.过点D作DG∥CF交射线AF于点G.
(1)求∠AFC的大小;
(2)求证:.
(3)如图2,连接OD,若OD⊥DG,求的值.
17.△ABC中,AB=AC,将△ABC绕C逆时针旋转得△DEC,旋转角为α,连接BD,AD,BE,DE.
(1)如图1,求证:△ADC∽△BEC;
(2)如图2,若∠BAC=90°,α=30°,EC=1,求BE的长;
(3)如图3,若∠BAD=∠BCD,AB=4,BE的长为x,△ABE的面积为y,求y与x的函数关系.
18.如图,已知△ABC是等边三角形,AB=8,M为AC中点,D为BC边上一动点,将AD绕点A逆时针旋转60°得到AE,连接CE、DE、ME.
(1)求证:CD+CE=CA;
(2)求出点M到CE所在直线的距离;
(3)当ME时,求CE的值.
参考答案
1.【解答】解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC4,
∵∠ACB=90°,△ABC绕点B顺时针旋转得到△A′BC′,点A′落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
Rt△A'BC中,A'C4,
∴AA'=AC+A'C=8;
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠A'BC'=∠ABC,BC'=BC=3,
∵CE∥A'B,
∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,
∴CE=BC=3,
Rt△ABC中,S△ABCAC BCAB CD,AC=4,BC=3,AB=5,
∴CD,
Rt△CED中,DE,
同理BD,
∴BE=DE+BD,C'E=BC'+BE=3,
∵CE∥A'B,
∴,
∴,
∴BM;
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°﹣∠ACB﹣∠BCC'=90°﹣∠BCC',
∠A'C'D=∠A'C'B﹣∠BC'C=90°﹣∠BC'C,
∴∠ACP=∠A'C'D,
∵AP∥A'C',
∴∠P=∠A'C'D,
∴∠P=∠ACP,
∴AP=AC,
∴AP=A'C',
在△APD和△A'C'D中,
,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点,
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DEA'C,
要使DE最小,只需A'C最小,此时A'、C、B共线,A'C的最小值为A'B﹣BC=AB﹣BC=2,
∴DE最小为A'C=1.
2.【解答】解:(1)∵四边形ABCD为矩形,
∴∠A=∠B=∠C=90°,
∵GH∥AB,
∴∠B=∠GHC=90°,∠A=∠PGD=90°,
∵EF∥AD,
∴∠PGD=∠HPF=90°,
∴四边形PFCH为矩形,
同理可得,四边形AGPE、GDFP、EPHB均为矩形,
∵AG=a,AE=b,AG:GD=AE:EB=1:2,
∴PE=a,PG=b,GD=PF=2a,EB=PH=2b,
∴四边形EBHP的面积=PE PH=2ab,四边形GPFD的面积=PG PF=2ab,
故答案为:=;
(2)∵PP1=PG,PP2=PE,
由(1)知PE PH=2ab,PG PF=2ab,
∴PP2 PH=PP1 PF,
即,
又∵∠FPP2=∠HPP1,
∴△PP2F∽△PP1H,
∴∠PFP2=∠PHP1,
∵∠P1QF=∠P2QH,
∴△P1FQ∽△P2HQ;
(3)连接P1P2、FH,
∵,,
∴,
∵∠P1PP2=∠C=90°,
∴△PP1P2∽△CFH,
∴,()2,
由(2)中△P1FQ∽△P2HQ,得,
∴,
∵∠P1QP2=∠FQH,
∴△P1QP2∽△FQH,
∴()2,
∵S1,S2=S△CFH+S△FQH,
∴S1S△CFHS△FQHS2,
∴.
3.【解答】解:(1)过点A作x轴的垂线,交MN于点E,交OB于点F,
由题意得:OQ=2t,OP=3t,PB=6﹣3t,
∵O(0,0),A(3,4),B(6,0),
∴OF=FB=3,AF=4,OA=AB,
∵MN∥OB,
∴∠OQM=∠OFA,∠OMQ=∠AOF,
∴△OQM∽△AFO,
∴,
∴,
∴QM,
∴点M的坐标是().
(2)∵MN∥OB,
∴四边形QEFO是矩形,
∴QE=OF,
∴ME=OF﹣QM=3,
∵OA=AB,
∴ME=NE,
∴MN=2ME=6﹣3t,
∴S四边形MNBP=S△MNP+S△BNP
MN OQ BP OQ
=﹣6t2+12t
=﹣6(t﹣1)2+6,
∵点P到达点B时,P、Q同时停止,
∴0<t<2,
∴t=1时,四边形MNBP的最大面积为6,四边形
MNBP
面积不存在最小值.
(3)∵MN=6﹣3t,BP=6﹣3t,
∴MN=BP,
∵MN∥BP,
∴四边形MNBP是平行四边形,
∴平分四边形MNBP面积的直线经过四边形的中心,即MB的中点,
设中点为H(x,y),
∵M(),B(6,0),
∴x,
y.
∴x,
化简得:y,
∴直线l的解析式为:y.
(4)①当t=0时,点M和点P均在点O处,∠BPN=∠OAP=0°,
此时点N在点B处,
∴点N到OA的距离为△OAB边OA上的高,记为h,
∵S△OABOB AFOA h,
∴6×45h,
∴点N到OA的距离为:h;
②当0<t<2时,
∵OQ=2t,QMt,
∴OMt,
∵MN∥OB,
∴,
∴OM=BNt,
∵OA=AB,
∴∠AOB=∠PBN,
又∵∠OAP=∠BPN,
∴△AOP∽△PBN,
∴,
∴,
解得:t1,t2=0(舍去).
∵MN=6﹣3t,AE=AF﹣OQ,ME=3,
∴MN=6﹣3,
AE,
ME,
∴AM.
设点N到OA的距离为h,
∵S△AMNMN AEAM h,
∴,
解得:h;
③当t=2时,不符合题意;
综上所述:点N到OA的距离为或.
4.【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
5.【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示:
∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AE=AF,
又∵∠BAC=∠EAF=30°,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∴∠ABE=∠ACD,
∵∠AOE=∠ABE+∠BAC,
∠AOE=∠ACD+∠BDC,
∴∠BDC=∠BAC=30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2所示:
证明:∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
又∵△ABC和△AEF都是等腰三角形,
∴AB=AC,AE=AF,
∴△BAE≌△CAF(SAS)
∴BE=CF,
∴∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)BF=CF+2AM,
理由如下:如图3所示:
∵△ABC和△AEF都是等腰三角形,
∴∠CAB=∠EAF=90°,AB=AC,AE=AF,
∴∠CAB﹣∠CAE=∠FAE﹣∠CAE,
即:∠BAE=∠CAF,
∴△BAE≌△CAE(SAS),
∴BE=CF,
∵AM⊥BF,AE=AF,∠EAF=90°,
∴EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM;
(4))如图4所示:
连接BD,以BD为直径作圆,
由题意,取满足条件的点P,P′,则PD=P′D=1.∠BPD=∠BP′D=90°,
∴BD=2,
∴BP,
连接PA,作AF⊥PB于点F,在BP上截取BE=PD,
∵∠PDA=ABE,AD=AB,
∴△ADP≌△ABE(SAS),
∴AP=AE,∠BAE=∠DAP,
∴∠PAE=90°,
由(3)可得:PB﹣PD=2AF,
∴AF,
∴S△PABPB AF,
同理可得:S△P′AB,
故△ABP的面积为:或.
6.【解答】(1)证明:如图1,
∵∠AOB=∠MON=90°,
∴∠AOB+∠AON=∠MON+∠AON,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴AM=BN;
(2)①证明:如图2,连接BN,
∵∠AOB=∠MON=90°,
∴∠AOB﹣∠BOM=∠MON﹣∠BOM,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴∠MAO=∠NBO=45°,AM=BN,
∴∠MBN=90°,
∴MB2+BN2=MN2,
∵△MON是等腰直角三角形,
∴MN2=2ON2,
∴AM2+BM2=2OM2;
②解:如图3,
当点N在线段AM上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x﹣3)2+x2=(4)2,
解得:x,
∴AM=BN,
如图4,
当点M在线段AN上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x+3)2+x2=(4)2,
解得:x,
∴AM=BN,
综上所述,线段AM的长为或.
7.【解答】解:(1)由题可得,a﹣c≥0,c﹣a≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45°,
又∵BD⊥AC,
∴∠ABD=45°,
又∵∠BOM=90°,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵b2,且a=c,
∴b=﹣2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
,
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,BC=2BO=4,
∴AN=4;
(3)如图3,连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,
由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
,
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
,
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD∠FPD=45°.
8.【解答】解:(1)如图,在EB延长线上取点C,使BG=DF,连接AG.
在Rt△ADF和Rt△ABG中,AD=AB,DF=BG,
∴Rt△ADF≌Rt△ABG(HL).
∴AG=AF,∠FAD=∠GAB,
∵∠EAB+∠FAD=∠EAF,
∴∠EAG=∠EAB+∠GAB=∠EAF.
在△EAG和△EAF中,AG=AF,∠EAG=∠EAF,AE=AE,
∴△EAG≌△EAF(SAS).
∴EF=GE=BG+BE=BE+DF.
故答案为:BE+DF=EF.
(2)结论:∠EAB+∠FAD=∠EAF.
理由:在EB延长线上取点G,使BG=DF,连接AG.
∵∠ABE+∠D=180°.
∴∠ABG=∠D.
在△ADF和△ABG中,AB=AD,∠ABG=∠D,BG=DF,
∴△ADF≌△ABG(SAS).
∴AF=AG,∠FAD=∠GAB.
在△AEF和△AEG中,AF=AG,EF=BE+DF=BE+BG=EG,AE=AF,
∴△AEF≌△AEG(SSS).
∴∠EAF=∠EAG,
∴∠EAF=∠GAB+∠EAB=∠EAB+∠FAD.
(3)在DF上取点H,使HF=EG.根据题意△CEG和△CFH都是直角三角形.
∵EC=FC,HF=EG,
∴Rt△CEG≌Rt△CFH(HL).
∴CG=CH,∠ECG=∠FCH,
又∵∠ECH+∠FCH=90°,
∴∠HCG=∠ECH+∠ECG=90°,
∴∠DCG=∠DCH=45°.
在△DCG和△DCH中,CG=CH,∠DCG=∠DCH,DC=DC,
∴△DCG≌△DCH(SAS),
∴DG=DH=DF﹣HF=DF﹣EG=6.
9.【解答】解:(1)∵等腰三角形APQ,∠AQP=120°,
∴∠APQ=∠QPA=30°,
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∴∠DAC=30°,
∴AD平分∠BAC,
∴AD⊥BC,
∴BDBC=3,
∴ADBD=3.
(2)∵∠BAC=60°,∠PAQ=30°,
∴∠BAP+∠CAD=30°∠BAC.
(3)①如图,当PD=PQ时.
∵∠APQ=∠QPA=30°,
∴∠PQD=∠APQ+∠QPA=60°,
∴△PDQ为等边三角形,
∴∠ADP=60°,
∴∠DPA=90°,
∴PDAD.
②如图1,∠PQD=60°,
故当△PDQ有任意两边相等时,
△PDQ为等边三角形,
∴∠PDQ=60°,
则∠PDQ与∠ACB重合.
如图2所示:
则PDBC.
综上所述,PD或.
(4)①如图,当此时AB=3BP时,过P作PM⊥AD.
∴AP=4,
∴PMAP=2,
∴AMPM=2,
∴MD=AD﹣AM,
∴PD.
②如图,当此时AB=3BP时,
把△ABP绕点A逆时针旋转60°得△ACN,连ND、NC,
过N作NM⊥BC,交BC延长线于M.
∴CN=PB=2,∠ACN=∠B=60°,∠CAN=∠BAP.
∵∠PAQ=30°,
∴∠BAP+∠DAC=30°,
∴∠CAN+∠DAC=30°,
∴∠DAN=∠PAD=30°.
在△PAD和△NAD中,
,
∴△PAD≌△NAD(SAS),
∴DP=DN.
∵∠NCM=180°﹣∠ACB﹣∠ACN=60°,
∴∠CNM=30°,
∴CMCN=1,
∴NMCM.
∵BP=2,
∴PC=4,
∴PN=PC+CN=5,
∴DN=PN﹣PD=5﹣x,
∵DN2+MN2=DM2,
∴(5﹣x)2+3=x2,
∴x.
∴PD.
综上所述,PD或.
10.【解答】证明:(1)延长ED至M使DM=DE,连接AM,
∵D为AB中点,
∴AD=BD,
在△BDE与△ADM中,
,
∴△BDE≌△ADM(SAS),
∴AM=BE,∠DAM=∠B,
∴AM∥BC,
∴∠MAF=180°﹣∠C=90°,
连接MF,
∵FD⊥ME,DE=DM,
∴MF=FE,
∴在Rt△MAF中,
AM2+AF2=MF2,
即:AF2+BE2=EF2;
解:(2)设AF=x,
∵AC=7,BC=5,CE=1,
则CF=AC﹣AF=7﹣x,
BE=BC﹣CE=4,
∵∠C=90°,
∴CF2+CE2=EF2,
即:EF2=(7﹣x)2+1,
由(1)知:MF=EF,∠BAF=90°,AM=BE,
∴MF2=(7﹣x)2+1,AM=4,
∵∠BAF=90°,
∴AF2+AM2=MF2,
即:x2+42=(7﹣x)2+1,
解得:x,
即:AF.
11.【解答】(1)证明:∵∠ABD=∠ADB,∠ABC=∠ADC=90°,
∴AB=AD,∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴A在BD的垂直平分上,∠CBD=∠CDB,
∴CB=CD,
∴C在BD的垂直平分上,
∴AC垂直平分BD;
(2)①证明:设∠F=α,
∵AB=AF,
∴∠ABF=∠F=α,
∵∠BAC是△ABF的外角,
∴∠BAC=∠F+∠AFB=2α,
由(1)AC⊥BD,CB=CD,
∴∠BCE=∠DCE,
∵BF∥CD,
∴∠F=∠DCE,
∴∠F=∠BCE=α,
∵∠ABC=90°,
∴∠BCE+∠BAC=90°,即α+2α=90°,
则α=30°,
∴∠DCB=2∠BCE=60°,
∵BC=CD,
∴△BCD是等边三角形;
②GH+AH为最小值时,GH与CH的数量关系是CH=2GH,
理由:
延长AD至A′,使DA′=AD,
∵CD⊥AD,
∴A与A′关于CD成轴对称,过A′作A′G⊥AC于G交CD于H,连接AH,
∴AH=A′H,
∴AH+GH=A′H+GH=A′G,此时GH+AH为最小,
由①知:∠DCE=30°,即∠GCH=30°,
∵A′G⊥AC即GH⊥CG,
∴在Rt△GCH中,∠GCH=30°,
∴CH=2GH,
∴GH+AH为最小值时,GH与CH的数量关系是CH=2GH.
12.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=45°,
∵DA=DC,DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE.
(2)解:∵EA=EF,
∴∠EAF=∠EFA.
设∠DCE=∠DAE=x,则∠DEC=∠DEA=135°﹣x,∠EAF=∠EFA=90°﹣x,
∴∠AEF=180°﹣2∠EAF=2x,
∴∠FEC=360°﹣2∠DEC﹣∠AEF=90°.
∵EF=EC,
∴∠ECF45°.
(3)解:GE2=BG2+ED2,证明如下,
将△BCG绕点C顺时针方向旋转90°得到△DCG',连接EG',
∵∠ECF=45°,
∴∠ECG'=∠DCG'+∠ECD=∠BCG+∠ECD=45°=∠ECG,
∵GC=G'C,EC=EC,
∴△GCE≌△G'CE(SAS),
∴EG=EG'.
∵∠EDG'=∠EDC+∠G'DC=45°+45°=90°,
∴ED2+G'D2=G'E2,
即GE2=BG2+ED2.
13.【解答】(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABD=∠ACE,
在△ABD 和△ACE 中,
,
∴△ABD≌△ACE(SAS)
∴∠BAD=∠CAE,
又∵∠BAC=90°,EH⊥AD于H交AB于K,
∴∠AKE=90°﹣∠BAD,∠KAE=90°﹣∠CAE,
∴∠AKE=∠KAE,
∴AE=EK;
(2)证明:如图,过点C作CH⊥AC,交FE的延长线于点P,
∴∠PCA=90°,AB=AC,
∵△ABC是等腰直角三角形,
∴∠ACB=∠ABC=45°,
∵BD=CE,
∴△ABD≌△ACE,
∴AD=AE,AB=PC=AC,
∴AD+EF=PE+EF=PF,
过G作QG⊥GC,使GC=GQ,
∴△GCQ是等腰直角三角形,
∴,
连接FQ,CQ,
∵GF⊥AG,GF=AG,
∴△AGF是等腰直角三角形,
∴△GAC≌△GFQ,
∴AC=FQ,∠GAC=∠GFQ=45°,
∴∠AFQ=∠AFG+∠GFQ=90°,
∴∠QFC=∠PCF=90°,
∴PC∥FQ,
∵AC=PC=FQ,
∴四边形FPCQ是平行四边形,
∴PF=CQ,
∵PF=AD+EF,
∴AD+EFCG;
(3)解:如图,过点A作AG⊥BC于G,过点M作MP⊥BC延长线于P,连接MC,连接GN交AM于H,过点N作NF∥AM交AB于F,
∵AE=ME,∠AEM=90°,
∴∠GAE+∠GEA=∠PEM+∠GEA=90°,
∴∠GAE=∠PEM,
在AGAE 和△PEM 中,
,
∴△GAE≌△PEM(AAS),
∴AG=EP,GE=PM,
又∵AG=GC,
∴GC=EP,
∴GC﹣EC=EP﹣EC,
∴GE=CP,
∴PM=CP,
∴∠MCP=45°
∵G为BC中点,N为BM中点,
∴GN∥CM,
∴∠NGC=45°,
∵N为BM中点,FN∥AM,
∴FN是△BAM的中位线,
∴F是AB的中点,FNAM,
在△AGN和△CGN 中,
,
.∴△GNA≌△CGN(SAS),
∴AN=CN,
∴ANAM=CN+NF,
∴如图,当C、N、F三点共线时,CN+NF 的值最小(两点之间,线段最短),
此时ANAM取得最小值,
∵∠MCP=∠ABC=45°,
∴MC I∥AF,
又∵NF∥AM,
∴四边形AFCM是平行四边形,
∴MC=FAAB=2,
∴MP=EG,AG=BG=CG2,
∴BD=CE=2,CD=2,
∴S△ACD CD AG326.
14.【解答】解:(1)∵AB=AC,∠ABC=30°,
∴∠ABC=∠ACB=30°,
∴∠BAC=180°﹣2∠ABC=120°,
由折叠可得:∠BAE=2∠BAD=2×15°=30°,AE=AB,
∴∠CAE=∠BAC﹣∠BAE=90°,
∴△ACE是等腰直角三角形,
∴CEAC=5;
(2)由折叠可得:∠BAE=2∠BAD=2α,AE=AB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
由(1)知:∠BAC=120°,
∴∠CAE=∠BAC﹣∠BAE=120°﹣2α,
∴∠AEC30°+α,
故答案为:30°+α;
(3)若△ACE是等边三角形,
∴∠CAE=∠AEC=60°,AC=CE=AE,
由(1)知:∠BAC=120°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAE=∠CAE,
∵AB=AC,
∴AE⊥BC且过O点,
即CO⊥AE,
∵AC=CE,
∴OE=OAAE,
∴CE=2OE,
在Rt△COE中,
由勾股定理可得:COOE,
∵点O为BC的中点,
∴CB=2OE=2OE,
∴;
15.【解答】(1)证明:如图1,连接AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴弧AD=弧AC,
∴AD=AC,
∴∠ADC=∠ACD,
∵点A、D、C、G在⊙O上,
∴∠FGC=∠ADC,
∵∠AGD=∠ACD,
∴∠FGC=∠AGD;
(2)解:∵AB是⊙O的直径,CD⊥AB于E点,
∴DE=0.5CD=0.5×8=4,
∠ADB=90°,
∵CD⊥AB,
∴∠ADB=∠BED=∠AED=90°,
∴∠AB D+∠BAD=90°,
∠BAD+∠ADE=90°,
∴∠ADE=∠ABD,
∴Rt△ADE∽Rt△DBE,
∴,
∴DE2=AE BE,
∵BE=2,
∴AE=AB﹣BE=AB﹣2,
∴16=(AB﹣2)×2,
解得:AB=10,
∴OB=0.5AB=5,
∴⊙O的半径为:5;
(3)解:如图,过点G作GH⊥DF于点H,
∵∠DAG+∠DCG=180°,
∠DCG+∠FCG=180°,
∴∠DAG=∠FCG,
∵弧AG=弧GC,
∴AG=CG,
∵∠AGD=∠FGC,
∴△DAGE≌△FCG(ASA),
∴CF=AD=3,DG=FG,
∵GH⊥DF,
∴DH=FH,
∵AB⊥CD,
∴DE=EC=2,
∴DF=2+2+3=7,
∴DH=HF=3.5,
∴AE,
∴AF2=AE2+EF2
∴FA,
∵GH∥AE,
∴,
∴,
∴FG,
16.【解答】解:(1)连接BF,
∵BE垂直平分AF,
∴BA=BF,
∴∠BOF=90°,∠ABO=∠OBF,
作BQ⊥CF于Q,
∴∠BQF=90°
又∵AB=BC,
∴BF=BC,
∴∠CBQ=∠FBQ,
∵∠CBQ+∠FBQ+∠ABO+∠OBF=∠ABC=90°,
∴∠FBQ+∠OBF=45°即∠OBQ=45°,
又∵∠BOF+∠BQF=180°,
而四边形OBQ内角和为360°,
∴∠OBQ+∠AFQ=180°,
∴∠AFQ=135°,即∠AFC=135°;
(2)证明:过点D作DH⊥AG于点H,如图所示:
∴∠DHG=90°,
由(1)知:∠AFC=135°,
∴∠CFG=180°﹣∠AFC=45°,
∵DG∥CF,
∴∠DGF=∠CFG=45°,
∴∠DGF=∠GDH=45°,
∴DH=HG,
在Rt△DHG中,DG2=DH2+GH2,
∴,
∵∠AOB=∠DHA=∠BAD=90°,
∴∠DAH+∠BAO=∠ABO+∠BAO=90°,即∠ABO=∠DAH,
∵BA=AD,
∴△ABO≌△DAH(AAS),
∴AO=DH,
∴;
(3)连接AC、CG,
由(1)可知∠AFC=135°,
∵∠AFC+∠CFG=180°,
∴∠CFG=45°,
∵DG∥CF,
∴∠DGF=∠CFG=45°,
∵OG⊥DG,
∴∠ODG=90°,
∵∠DGF+∠DOG=90°,
∴∠DGF=∠DOG=45°,
∴△ODG是等腰直角三角形,
∴OGDG,CD=DG,
由(2)知AFDG,
∴AF=OG,
∴AO=FG,
∴AO=CG,
∵AF=2OA,
∴2OADG=2CG,
∴CG,
∴AG=AF+FGDGDGDG,
又∵AC为正方形ABCD对角线,
∴ACAD,
在RT△AGC中由勾股定理得:
AC2=CG2+AG2,
∴,
解得:.
17.【解答】(1)证明:如图1,
由旋转得,DC=AC,BC=EC,
∴AC:BC=DC:EC,
∵∠ACD=∠BCE=α,
∴△ADC∽△BEC.
(2)如图2,设DE,BC交于点M,
作MN⊥EC于N,
设MN=x,
∵∠MEN=45°,
∴EN=x,
∵∠MCN=30°,
∴CNx,
∵CE1,即x+x1,
∴x=1,
∴MEx,
∵∠EBM=∠ENB,
∴BE=EM.
(3)延长AB,作EF⊥AB于F,
设∠BAD=∠BCD=β,
∴∠ACB=α+β,
∵CA=CD,∠ACD=α,
∴∠CAD=90°α,
∴∠BAC=90°α+β,
∴90°α+β+2(α+β)=180°,
整理得,α+β=30°,
∵∠ABC=∠ACB=α+β,∠CAD=∠EBC=90°α,
∴∠EBF=180°﹣(α+β)﹣(90°α)=90﹣(α+β)=60°,
∵BE的长为x,
∴EF=sin60° xx,
∵AB=4,
∴△ABE的面积为y=4x,
∴.
18.【解答】解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵AD绕点A逆时针旋转60°得到AE,
∴AD=AE,∠DAE=60°,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵BC=BD+CD,
∴BC=CE+CD,
∴CD+CE=CA,
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE=60°,
∵点M为AC的中点,AC=AB=8,
∴AM=CMAC=4,
过点M作MH⊥CE所在的直线于点H,
∴∠MHC=90°,∠CMH=30°,
∴CH,
∴MH2.
(3)过点M作MH⊥CE所在的直线于点H,
由(2)可知MH=2,CH=2,
在Rt△MHE中,∠MHE=90°,ME,
∴HE,
当点H落在线段CE上时,
CE=CH+HE=2,
当点H落在线段CE的延长线上时,
CE=CH﹣HE=2,
∴CE的值为或.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺练习几何压轴题训练
1.在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
2.如图,在矩形ABCD中,线段EF、GH分别平行于AD、AB,它们相交于点P,点P1、P2分别在线段PF、PH上,PP1=PG,PP2=PE,连接P1H、P2F,P1H与P2F相交于点Q.已知AG:GD=AE:EB=1:2,设AG=a,AE=b.
(1)四边形EBHP的面积 四边形GPFD的面积(填“>”、“=”或“<”)
(2)求证:△P1FQ∽△P2HQ;
(3)设四边形PP1QP2的面积为S1,四边形CFQH的面积为S2,求的值.
3.如图,△OAB的顶点坐标分别为O(0,0),A(3,4),B(6,0),动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作MN∥OB分别交AO、AB于点M、N,连接PM、PN.设运动时间为t(秒).
(1)求点M的坐标(用含t的式子表示);
(2)求四边形MNBP面积的最大值或最小值;
(3)是否存在这样的直线l,总能平分四边形MNBP的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;
(4)连接AP,当∠OAP=∠BPN时,求点N到OA的距离.
4.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
5.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: ,∠BDC= °;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系: ;
(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP= .
6.已知△AOB和△MON都是等腰直角三角形(OA<OM<OA),∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:AM=BN;
(2)将△MON绕点O顺时针旋转.
①如图2,当点M恰好在AB边上时,求证:AM2+BM2=2OM2;
②当点A,M,N在同一条直线上时,若OA=4,OM=3,请直接写出线段AM的长.
7.如图,△ABC中,A(a,0),B(b,0),C(0,c),且满足b2,
(1)BD⊥AC于D,交y轴于M,求M点坐标;
(2)过点A作AG⊥BC于G,交OC于N,若∠CAN=15°,求AN的长;
(3)P为第一象限一点,PQ⊥PA交y轴于Q.在PQ上截取PE=PA,F为CE的中点,求∠OPF的度数.
8.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠ADC=90°,点E、F分别在边BC、CD上,若∠EAB+∠FAD=∠EAF则线段BE、DF、EF之间的数量关系是 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,若EF=BE+FD,探究∠EAB、∠FAD、∠EAF的之间的数量关系,并说明理由.
(3)如图3,在△ABC中,AB=AC,∠BAC=90°,E是线段AB上一点,CE⊥CF,且CE=CF,过点F作FD⊥FC交CA的延长线于D,过E作EG⊥EC交BC于G,连接DG.若DF=7,EG=1,求DG的长.
9.如图①,△ABC是等边三角形,AB=6.点P从点A出发,沿折线AB﹣BC运动.当点P不与点A重合时,连结AP,以AP为边向其右侧作等腰三角形APQ,使∠AQP=120°,延长AQ交边BC于点D,当点D与点C重合,点P停止运动,连结PD
(1)当点P在边AB上运动时,AD的长为 .
(2)如图②,当点P在边BC上时,求证:.
(3)点P在整个运动过程中,当△PDQ是轴对称图形时,求PD的长.
(4)点P在整个运动过程中,当AB=3BP时,直接写出PD的长
10.如图,Rt△ABC中,∠ACB=90°,D为AB中点,点E在BC边上(点E不与点B,C重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF.
(1)求证:AF2+BE2=EF2
(2)若AC=7,BC=5,EC=1,直接写出线段AF的长.
11.如图,∠ABC=∠ADC=90°,AC与BD相交于点E,∠ABD=∠ADB.
(1)求证:AC垂直平分BD;
(2)过点B作BF∥CD交CA的延长线于F,如果AB=AF;
①求证:△BCD是等边三角形;
②如果G、H分别是线段AC、线段CD上的动点,当GH+AH为最小值时,请确定点H的位置,并思考此时GH与CH有怎样的数量关系.
12.如图,点E在正方形ABCD对角线BD上,连接AE、CE,点F为AB上一点,连接CF,
交BD于点G.连接EF,若AE=EF.
(1)求证:AE=CE;
(2)求∠ECF的度数;
(3)经探究,DE、BG、EG三条线段满足某种数量关系,请直接写出们之间的关系式.
13.如图,在△ABC中,∠BAC=90°,AB=AC,D,E分别为BC上两动点,BD=CE.
(1)如图1,若EH⊥AD于H交AB于K,求证:AE=EK;
(2)如图2,若EF∥AD交AC于F,GF⊥AG,AG=GF,求证:;
(3)如图3,若AB=4,将AE绕点E顺时针旋转90°得EM,N为BM中点,当取得最小值时,请直接写出△ACD的面积.
14.如图,在等腰三角形ABC中,AB=AC,∠ABC=30°,点O为BC的中点,点D是线段OB上的动点(点D不与点O,B重合),将△ABD沿直线AD折叠得到△AED,连接CE.
(1)若AB=AC=5,∠BAD=15°,求CE的长;
(2)若∠BAD=α,则∠AEC= ;
(3)若△ACE是等边三角形,请直接写出的值.
15.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG与DC的延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若CD=8,BE=2,求⊙O的半径长;
(3)若G是的中点,CECF=2,求GF的长.
16.如图1,F为正方形ABCD内一点,点E在边AD上(不与端点A,D重合),BE垂直平分AF交AF于点O,连接CF.过点D作DG∥CF交射线AF于点G.
(1)求∠AFC的大小;
(2)求证:.
(3)如图2,连接OD,若OD⊥DG,求的值.
17.△ABC中,AB=AC,将△ABC绕C逆时针旋转得△DEC,旋转角为α,连接BD,AD,BE,DE.
(1)如图1,求证:△ADC∽△BEC;
(2)如图2,若∠BAC=90°,α=30°,EC=1,求BE的长;
(3)如图3,若∠BAD=∠BCD,AB=4,BE的长为x,△ABE的面积为y,求y与x的函数关系.
18.如图,已知△ABC是等边三角形,AB=8,M为AC中点,D为BC边上一动点,将AD绕点A逆时针旋转60°得到AE,连接CE、DE、ME.
(1)求证:CD+CE=CA;
(2)求出点M到CE所在直线的距离;
(3)当ME时,求CE的值.
参考答案
1.【解答】解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC4,
∵∠ACB=90°,△ABC绕点B顺时针旋转得到△A′BC′,点A′落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
Rt△A'BC中,A'C4,
∴AA'=AC+A'C=8;
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠A'BC'=∠ABC,BC'=BC=3,
∵CE∥A'B,
∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,
∴CE=BC=3,
Rt△ABC中,S△ABCAC BCAB CD,AC=4,BC=3,AB=5,
∴CD,
Rt△CED中,DE,
同理BD,
∴BE=DE+BD,C'E=BC'+BE=3,
∵CE∥A'B,
∴,
∴,
∴BM;
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°﹣∠ACB﹣∠BCC'=90°﹣∠BCC',
∠A'C'D=∠A'C'B﹣∠BC'C=90°﹣∠BC'C,
∴∠ACP=∠A'C'D,
∵AP∥A'C',
∴∠P=∠A'C'D,
∴∠P=∠ACP,
∴AP=AC,
∴AP=A'C',
在△APD和△A'C'D中,
,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点,
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DEA'C,
要使DE最小,只需A'C最小,此时A'、C、B共线,A'C的最小值为A'B﹣BC=AB﹣BC=2,
∴DE最小为A'C=1.
2.【解答】解:(1)∵四边形ABCD为矩形,
∴∠A=∠B=∠C=90°,
∵GH∥AB,
∴∠B=∠GHC=90°,∠A=∠PGD=90°,
∵EF∥AD,
∴∠PGD=∠HPF=90°,
∴四边形PFCH为矩形,
同理可得,四边形AGPE、GDFP、EPHB均为矩形,
∵AG=a,AE=b,AG:GD=AE:EB=1:2,
∴PE=a,PG=b,GD=PF=2a,EB=PH=2b,
∴四边形EBHP的面积=PE PH=2ab,四边形GPFD的面积=PG PF=2ab,
故答案为:=;
(2)∵PP1=PG,PP2=PE,
由(1)知PE PH=2ab,PG PF=2ab,
∴PP2 PH=PP1 PF,
即,
又∵∠FPP2=∠HPP1,
∴△PP2F∽△PP1H,
∴∠PFP2=∠PHP1,
∵∠P1QF=∠P2QH,
∴△P1FQ∽△P2HQ;
(3)连接P1P2、FH,
∵,,
∴,
∵∠P1PP2=∠C=90°,
∴△PP1P2∽△CFH,
∴,()2,
由(2)中△P1FQ∽△P2HQ,得,
∴,
∵∠P1QP2=∠FQH,
∴△P1QP2∽△FQH,
∴()2,
∵S1,S2=S△CFH+S△FQH,
∴S1S△CFHS△FQHS2,
∴.
3.【解答】解:(1)过点A作x轴的垂线,交MN于点E,交OB于点F,
由题意得:OQ=2t,OP=3t,PB=6﹣3t,
∵O(0,0),A(3,4),B(6,0),
∴OF=FB=3,AF=4,OA=AB,
∵MN∥OB,
∴∠OQM=∠OFA,∠OMQ=∠AOF,
∴△OQM∽△AFO,
∴,
∴,
∴QM,
∴点M的坐标是().
(2)∵MN∥OB,
∴四边形QEFO是矩形,
∴QE=OF,
∴ME=OF﹣QM=3,
∵OA=AB,
∴ME=NE,
∴MN=2ME=6﹣3t,
∴S四边形MNBP=S△MNP+S△BNP
MN OQ BP OQ
=﹣6t2+12t
=﹣6(t﹣1)2+6,
∵点P到达点B时,P、Q同时停止,
∴0<t<2,
∴t=1时,四边形MNBP的最大面积为6,四边形
MNBP
面积不存在最小值.
(3)∵MN=6﹣3t,BP=6﹣3t,
∴MN=BP,
∵MN∥BP,
∴四边形MNBP是平行四边形,
∴平分四边形MNBP面积的直线经过四边形的中心,即MB的中点,
设中点为H(x,y),
∵M(),B(6,0),
∴x,
y.
∴x,
化简得:y,
∴直线l的解析式为:y.
(4)①当t=0时,点M和点P均在点O处,∠BPN=∠OAP=0°,
此时点N在点B处,
∴点N到OA的距离为△OAB边OA上的高,记为h,
∵S△OABOB AFOA h,
∴6×45h,
∴点N到OA的距离为:h;
②当0<t<2时,
∵OQ=2t,QMt,
∴OMt,
∵MN∥OB,
∴,
∴OM=BNt,
∵OA=AB,
∴∠AOB=∠PBN,
又∵∠OAP=∠BPN,
∴△AOP∽△PBN,
∴,
∴,
解得:t1,t2=0(舍去).
∵MN=6﹣3t,AE=AF﹣OQ,ME=3,
∴MN=6﹣3,
AE,
ME,
∴AM.
设点N到OA的距离为h,
∵S△AMNMN AEAM h,
∴,
解得:h;
③当t=2时,不符合题意;
综上所述:点N到OA的距离为或.
4.【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
5.【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示:
∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AE=AF,
又∵∠BAC=∠EAF=30°,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∴∠ABE=∠ACD,
∵∠AOE=∠ABE+∠BAC,
∠AOE=∠ACD+∠BDC,
∴∠BDC=∠BAC=30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2所示:
证明:∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
又∵△ABC和△AEF都是等腰三角形,
∴AB=AC,AE=AF,
∴△BAE≌△CAF(SAS)
∴BE=CF,
∴∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)BF=CF+2AM,
理由如下:如图3所示:
∵△ABC和△AEF都是等腰三角形,
∴∠CAB=∠EAF=90°,AB=AC,AE=AF,
∴∠CAB﹣∠CAE=∠FAE﹣∠CAE,
即:∠BAE=∠CAF,
∴△BAE≌△CAE(SAS),
∴BE=CF,
∵AM⊥BF,AE=AF,∠EAF=90°,
∴EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM;
(4))如图4所示:
连接BD,以BD为直径作圆,
由题意,取满足条件的点P,P′,则PD=P′D=1.∠BPD=∠BP′D=90°,
∴BD=2,
∴BP,
连接PA,作AF⊥PB于点F,在BP上截取BE=PD,
∵∠PDA=ABE,AD=AB,
∴△ADP≌△ABE(SAS),
∴AP=AE,∠BAE=∠DAP,
∴∠PAE=90°,
由(3)可得:PB﹣PD=2AF,
∴AF,
∴S△PABPB AF,
同理可得:S△P′AB,
故△ABP的面积为:或.
6.【解答】(1)证明:如图1,
∵∠AOB=∠MON=90°,
∴∠AOB+∠AON=∠MON+∠AON,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴AM=BN;
(2)①证明:如图2,连接BN,
∵∠AOB=∠MON=90°,
∴∠AOB﹣∠BOM=∠MON﹣∠BOM,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴∠MAO=∠NBO=45°,AM=BN,
∴∠MBN=90°,
∴MB2+BN2=MN2,
∵△MON是等腰直角三角形,
∴MN2=2ON2,
∴AM2+BM2=2OM2;
②解:如图3,
当点N在线段AM上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x﹣3)2+x2=(4)2,
解得:x,
∴AM=BN,
如图4,
当点M在线段AN上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x+3)2+x2=(4)2,
解得:x,
∴AM=BN,
综上所述,线段AM的长为或.
7.【解答】解:(1)由题可得,a﹣c≥0,c﹣a≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45°,
又∵BD⊥AC,
∴∠ABD=45°,
又∵∠BOM=90°,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵b2,且a=c,
∴b=﹣2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
,
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,BC=2BO=4,
∴AN=4;
(3)如图3,连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,
由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
,
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
,
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD∠FPD=45°.
8.【解答】解:(1)如图,在EB延长线上取点C,使BG=DF,连接AG.
在Rt△ADF和Rt△ABG中,AD=AB,DF=BG,
∴Rt△ADF≌Rt△ABG(HL).
∴AG=AF,∠FAD=∠GAB,
∵∠EAB+∠FAD=∠EAF,
∴∠EAG=∠EAB+∠GAB=∠EAF.
在△EAG和△EAF中,AG=AF,∠EAG=∠EAF,AE=AE,
∴△EAG≌△EAF(SAS).
∴EF=GE=BG+BE=BE+DF.
故答案为:BE+DF=EF.
(2)结论:∠EAB+∠FAD=∠EAF.
理由:在EB延长线上取点G,使BG=DF,连接AG.
∵∠ABE+∠D=180°.
∴∠ABG=∠D.
在△ADF和△ABG中,AB=AD,∠ABG=∠D,BG=DF,
∴△ADF≌△ABG(SAS).
∴AF=AG,∠FAD=∠GAB.
在△AEF和△AEG中,AF=AG,EF=BE+DF=BE+BG=EG,AE=AF,
∴△AEF≌△AEG(SSS).
∴∠EAF=∠EAG,
∴∠EAF=∠GAB+∠EAB=∠EAB+∠FAD.
(3)在DF上取点H,使HF=EG.根据题意△CEG和△CFH都是直角三角形.
∵EC=FC,HF=EG,
∴Rt△CEG≌Rt△CFH(HL).
∴CG=CH,∠ECG=∠FCH,
又∵∠ECH+∠FCH=90°,
∴∠HCG=∠ECH+∠ECG=90°,
∴∠DCG=∠DCH=45°.
在△DCG和△DCH中,CG=CH,∠DCG=∠DCH,DC=DC,
∴△DCG≌△DCH(SAS),
∴DG=DH=DF﹣HF=DF﹣EG=6.
9.【解答】解:(1)∵等腰三角形APQ,∠AQP=120°,
∴∠APQ=∠QPA=30°,
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∴∠DAC=30°,
∴AD平分∠BAC,
∴AD⊥BC,
∴BDBC=3,
∴ADBD=3.
(2)∵∠BAC=60°,∠PAQ=30°,
∴∠BAP+∠CAD=30°∠BAC.
(3)①如图,当PD=PQ时.
∵∠APQ=∠QPA=30°,
∴∠PQD=∠APQ+∠QPA=60°,
∴△PDQ为等边三角形,
∴∠ADP=60°,
∴∠DPA=90°,
∴PDAD.
②如图1,∠PQD=60°,
故当△PDQ有任意两边相等时,
△PDQ为等边三角形,
∴∠PDQ=60°,
则∠PDQ与∠ACB重合.
如图2所示:
则PDBC.
综上所述,PD或.
(4)①如图,当此时AB=3BP时,过P作PM⊥AD.
∴AP=4,
∴PMAP=2,
∴AMPM=2,
∴MD=AD﹣AM,
∴PD.
②如图,当此时AB=3BP时,
把△ABP绕点A逆时针旋转60°得△ACN,连ND、NC,
过N作NM⊥BC,交BC延长线于M.
∴CN=PB=2,∠ACN=∠B=60°,∠CAN=∠BAP.
∵∠PAQ=30°,
∴∠BAP+∠DAC=30°,
∴∠CAN+∠DAC=30°,
∴∠DAN=∠PAD=30°.
在△PAD和△NAD中,
,
∴△PAD≌△NAD(SAS),
∴DP=DN.
∵∠NCM=180°﹣∠ACB﹣∠ACN=60°,
∴∠CNM=30°,
∴CMCN=1,
∴NMCM.
∵BP=2,
∴PC=4,
∴PN=PC+CN=5,
∴DN=PN﹣PD=5﹣x,
∵DN2+MN2=DM2,
∴(5﹣x)2+3=x2,
∴x.
∴PD.
综上所述,PD或.
10.【解答】证明:(1)延长ED至M使DM=DE,连接AM,
∵D为AB中点,
∴AD=BD,
在△BDE与△ADM中,
,
∴△BDE≌△ADM(SAS),
∴AM=BE,∠DAM=∠B,
∴AM∥BC,
∴∠MAF=180°﹣∠C=90°,
连接MF,
∵FD⊥ME,DE=DM,
∴MF=FE,
∴在Rt△MAF中,
AM2+AF2=MF2,
即:AF2+BE2=EF2;
解:(2)设AF=x,
∵AC=7,BC=5,CE=1,
则CF=AC﹣AF=7﹣x,
BE=BC﹣CE=4,
∵∠C=90°,
∴CF2+CE2=EF2,
即:EF2=(7﹣x)2+1,
由(1)知:MF=EF,∠BAF=90°,AM=BE,
∴MF2=(7﹣x)2+1,AM=4,
∵∠BAF=90°,
∴AF2+AM2=MF2,
即:x2+42=(7﹣x)2+1,
解得:x,
即:AF.
11.【解答】(1)证明:∵∠ABD=∠ADB,∠ABC=∠ADC=90°,
∴AB=AD,∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴A在BD的垂直平分上,∠CBD=∠CDB,
∴CB=CD,
∴C在BD的垂直平分上,
∴AC垂直平分BD;
(2)①证明:设∠F=α,
∵AB=AF,
∴∠ABF=∠F=α,
∵∠BAC是△ABF的外角,
∴∠BAC=∠F+∠AFB=2α,
由(1)AC⊥BD,CB=CD,
∴∠BCE=∠DCE,
∵BF∥CD,
∴∠F=∠DCE,
∴∠F=∠BCE=α,
∵∠ABC=90°,
∴∠BCE+∠BAC=90°,即α+2α=90°,
则α=30°,
∴∠DCB=2∠BCE=60°,
∵BC=CD,
∴△BCD是等边三角形;
②GH+AH为最小值时,GH与CH的数量关系是CH=2GH,
理由:
延长AD至A′,使DA′=AD,
∵CD⊥AD,
∴A与A′关于CD成轴对称,过A′作A′G⊥AC于G交CD于H,连接AH,
∴AH=A′H,
∴AH+GH=A′H+GH=A′G,此时GH+AH为最小,
由①知:∠DCE=30°,即∠GCH=30°,
∵A′G⊥AC即GH⊥CG,
∴在Rt△GCH中,∠GCH=30°,
∴CH=2GH,
∴GH+AH为最小值时,GH与CH的数量关系是CH=2GH.
12.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=45°,
∵DA=DC,DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE.
(2)解:∵EA=EF,
∴∠EAF=∠EFA.
设∠DCE=∠DAE=x,则∠DEC=∠DEA=135°﹣x,∠EAF=∠EFA=90°﹣x,
∴∠AEF=180°﹣2∠EAF=2x,
∴∠FEC=360°﹣2∠DEC﹣∠AEF=90°.
∵EF=EC,
∴∠ECF45°.
(3)解:GE2=BG2+ED2,证明如下,
将△BCG绕点C顺时针方向旋转90°得到△DCG',连接EG',
∵∠ECF=45°,
∴∠ECG'=∠DCG'+∠ECD=∠BCG+∠ECD=45°=∠ECG,
∵GC=G'C,EC=EC,
∴△GCE≌△G'CE(SAS),
∴EG=EG'.
∵∠EDG'=∠EDC+∠G'DC=45°+45°=90°,
∴ED2+G'D2=G'E2,
即GE2=BG2+ED2.
13.【解答】(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABD=∠ACE,
在△ABD 和△ACE 中,
,
∴△ABD≌△ACE(SAS)
∴∠BAD=∠CAE,
又∵∠BAC=90°,EH⊥AD于H交AB于K,
∴∠AKE=90°﹣∠BAD,∠KAE=90°﹣∠CAE,
∴∠AKE=∠KAE,
∴AE=EK;
(2)证明:如图,过点C作CH⊥AC,交FE的延长线于点P,
∴∠PCA=90°,AB=AC,
∵△ABC是等腰直角三角形,
∴∠ACB=∠ABC=45°,
∵BD=CE,
∴△ABD≌△ACE,
∴AD=AE,AB=PC=AC,
∴AD+EF=PE+EF=PF,
过G作QG⊥GC,使GC=GQ,
∴△GCQ是等腰直角三角形,
∴,
连接FQ,CQ,
∵GF⊥AG,GF=AG,
∴△AGF是等腰直角三角形,
∴△GAC≌△GFQ,
∴AC=FQ,∠GAC=∠GFQ=45°,
∴∠AFQ=∠AFG+∠GFQ=90°,
∴∠QFC=∠PCF=90°,
∴PC∥FQ,
∵AC=PC=FQ,
∴四边形FPCQ是平行四边形,
∴PF=CQ,
∵PF=AD+EF,
∴AD+EFCG;
(3)解:如图,过点A作AG⊥BC于G,过点M作MP⊥BC延长线于P,连接MC,连接GN交AM于H,过点N作NF∥AM交AB于F,
∵AE=ME,∠AEM=90°,
∴∠GAE+∠GEA=∠PEM+∠GEA=90°,
∴∠GAE=∠PEM,
在AGAE 和△PEM 中,
,
∴△GAE≌△PEM(AAS),
∴AG=EP,GE=PM,
又∵AG=GC,
∴GC=EP,
∴GC﹣EC=EP﹣EC,
∴GE=CP,
∴PM=CP,
∴∠MCP=45°
∵G为BC中点,N为BM中点,
∴GN∥CM,
∴∠NGC=45°,
∵N为BM中点,FN∥AM,
∴FN是△BAM的中位线,
∴F是AB的中点,FNAM,
在△AGN和△CGN 中,
,
.∴△GNA≌△CGN(SAS),
∴AN=CN,
∴ANAM=CN+NF,
∴如图,当C、N、F三点共线时,CN+NF 的值最小(两点之间,线段最短),
此时ANAM取得最小值,
∵∠MCP=∠ABC=45°,
∴MC I∥AF,
又∵NF∥AM,
∴四边形AFCM是平行四边形,
∴MC=FAAB=2,
∴MP=EG,AG=BG=CG2,
∴BD=CE=2,CD=2,
∴S△ACD CD AG326.
14.【解答】解:(1)∵AB=AC,∠ABC=30°,
∴∠ABC=∠ACB=30°,
∴∠BAC=180°﹣2∠ABC=120°,
由折叠可得:∠BAE=2∠BAD=2×15°=30°,AE=AB,
∴∠CAE=∠BAC﹣∠BAE=90°,
∴△ACE是等腰直角三角形,
∴CEAC=5;
(2)由折叠可得:∠BAE=2∠BAD=2α,AE=AB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
由(1)知:∠BAC=120°,
∴∠CAE=∠BAC﹣∠BAE=120°﹣2α,
∴∠AEC30°+α,
故答案为:30°+α;
(3)若△ACE是等边三角形,
∴∠CAE=∠AEC=60°,AC=CE=AE,
由(1)知:∠BAC=120°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAE=∠CAE,
∵AB=AC,
∴AE⊥BC且过O点,
即CO⊥AE,
∵AC=CE,
∴OE=OAAE,
∴CE=2OE,
在Rt△COE中,
由勾股定理可得:COOE,
∵点O为BC的中点,
∴CB=2OE=2OE,
∴;
15.【解答】(1)证明:如图1,连接AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴弧AD=弧AC,
∴AD=AC,
∴∠ADC=∠ACD,
∵点A、D、C、G在⊙O上,
∴∠FGC=∠ADC,
∵∠AGD=∠ACD,
∴∠FGC=∠AGD;
(2)解:∵AB是⊙O的直径,CD⊥AB于E点,
∴DE=0.5CD=0.5×8=4,
∠ADB=90°,
∵CD⊥AB,
∴∠ADB=∠BED=∠AED=90°,
∴∠AB D+∠BAD=90°,
∠BAD+∠ADE=90°,
∴∠ADE=∠ABD,
∴Rt△ADE∽Rt△DBE,
∴,
∴DE2=AE BE,
∵BE=2,
∴AE=AB﹣BE=AB﹣2,
∴16=(AB﹣2)×2,
解得:AB=10,
∴OB=0.5AB=5,
∴⊙O的半径为:5;
(3)解:如图,过点G作GH⊥DF于点H,
∵∠DAG+∠DCG=180°,
∠DCG+∠FCG=180°,
∴∠DAG=∠FCG,
∵弧AG=弧GC,
∴AG=CG,
∵∠AGD=∠FGC,
∴△DAGE≌△FCG(ASA),
∴CF=AD=3,DG=FG,
∵GH⊥DF,
∴DH=FH,
∵AB⊥CD,
∴DE=EC=2,
∴DF=2+2+3=7,
∴DH=HF=3.5,
∴AE,
∴AF2=AE2+EF2
∴FA,
∵GH∥AE,
∴,
∴,
∴FG,
16.【解答】解:(1)连接BF,
∵BE垂直平分AF,
∴BA=BF,
∴∠BOF=90°,∠ABO=∠OBF,
作BQ⊥CF于Q,
∴∠BQF=90°
又∵AB=BC,
∴BF=BC,
∴∠CBQ=∠FBQ,
∵∠CBQ+∠FBQ+∠ABO+∠OBF=∠ABC=90°,
∴∠FBQ+∠OBF=45°即∠OBQ=45°,
又∵∠BOF+∠BQF=180°,
而四边形OBQ内角和为360°,
∴∠OBQ+∠AFQ=180°,
∴∠AFQ=135°,即∠AFC=135°;
(2)证明:过点D作DH⊥AG于点H,如图所示:
∴∠DHG=90°,
由(1)知:∠AFC=135°,
∴∠CFG=180°﹣∠AFC=45°,
∵DG∥CF,
∴∠DGF=∠CFG=45°,
∴∠DGF=∠GDH=45°,
∴DH=HG,
在Rt△DHG中,DG2=DH2+GH2,
∴,
∵∠AOB=∠DHA=∠BAD=90°,
∴∠DAH+∠BAO=∠ABO+∠BAO=90°,即∠ABO=∠DAH,
∵BA=AD,
∴△ABO≌△DAH(AAS),
∴AO=DH,
∴;
(3)连接AC、CG,
由(1)可知∠AFC=135°,
∵∠AFC+∠CFG=180°,
∴∠CFG=45°,
∵DG∥CF,
∴∠DGF=∠CFG=45°,
∵OG⊥DG,
∴∠ODG=90°,
∵∠DGF+∠DOG=90°,
∴∠DGF=∠DOG=45°,
∴△ODG是等腰直角三角形,
∴OGDG,CD=DG,
由(2)知AFDG,
∴AF=OG,
∴AO=FG,
∴AO=CG,
∵AF=2OA,
∴2OADG=2CG,
∴CG,
∴AG=AF+FGDGDGDG,
又∵AC为正方形ABCD对角线,
∴ACAD,
在RT△AGC中由勾股定理得:
AC2=CG2+AG2,
∴,
解得:.
17.【解答】(1)证明:如图1,
由旋转得,DC=AC,BC=EC,
∴AC:BC=DC:EC,
∵∠ACD=∠BCE=α,
∴△ADC∽△BEC.
(2)如图2,设DE,BC交于点M,
作MN⊥EC于N,
设MN=x,
∵∠MEN=45°,
∴EN=x,
∵∠MCN=30°,
∴CNx,
∵CE1,即x+x1,
∴x=1,
∴MEx,
∵∠EBM=∠ENB,
∴BE=EM.
(3)延长AB,作EF⊥AB于F,
设∠BAD=∠BCD=β,
∴∠ACB=α+β,
∵CA=CD,∠ACD=α,
∴∠CAD=90°α,
∴∠BAC=90°α+β,
∴90°α+β+2(α+β)=180°,
整理得,α+β=30°,
∵∠ABC=∠ACB=α+β,∠CAD=∠EBC=90°α,
∴∠EBF=180°﹣(α+β)﹣(90°α)=90﹣(α+β)=60°,
∵BE的长为x,
∴EF=sin60° xx,
∵AB=4,
∴△ABE的面积为y=4x,
∴.
18.【解答】解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵AD绕点A逆时针旋转60°得到AE,
∴AD=AE,∠DAE=60°,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵BC=BD+CD,
∴BC=CE+CD,
∴CD+CE=CA,
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE=60°,
∵点M为AC的中点,AC=AB=8,
∴AM=CMAC=4,
过点M作MH⊥CE所在的直线于点H,
∴∠MHC=90°,∠CMH=30°,
∴CH,
∴MH2.
(3)过点M作MH⊥CE所在的直线于点H,
由(2)可知MH=2,CH=2,
在Rt△MHE中,∠MHE=90°,ME,
∴HE,
当点H落在线段CE上时,
CE=CH+HE=2,
当点H落在线段CE的延长线上时,
CE=CH﹣HE=2,
∴CE的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
