2025年九年级数学中考三轮冲刺训练动点问题的函数图象问题选填题(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练动点问题的函数图象问题选填题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 19:31:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练动点问题的函数图象问题选填题
一、选择题
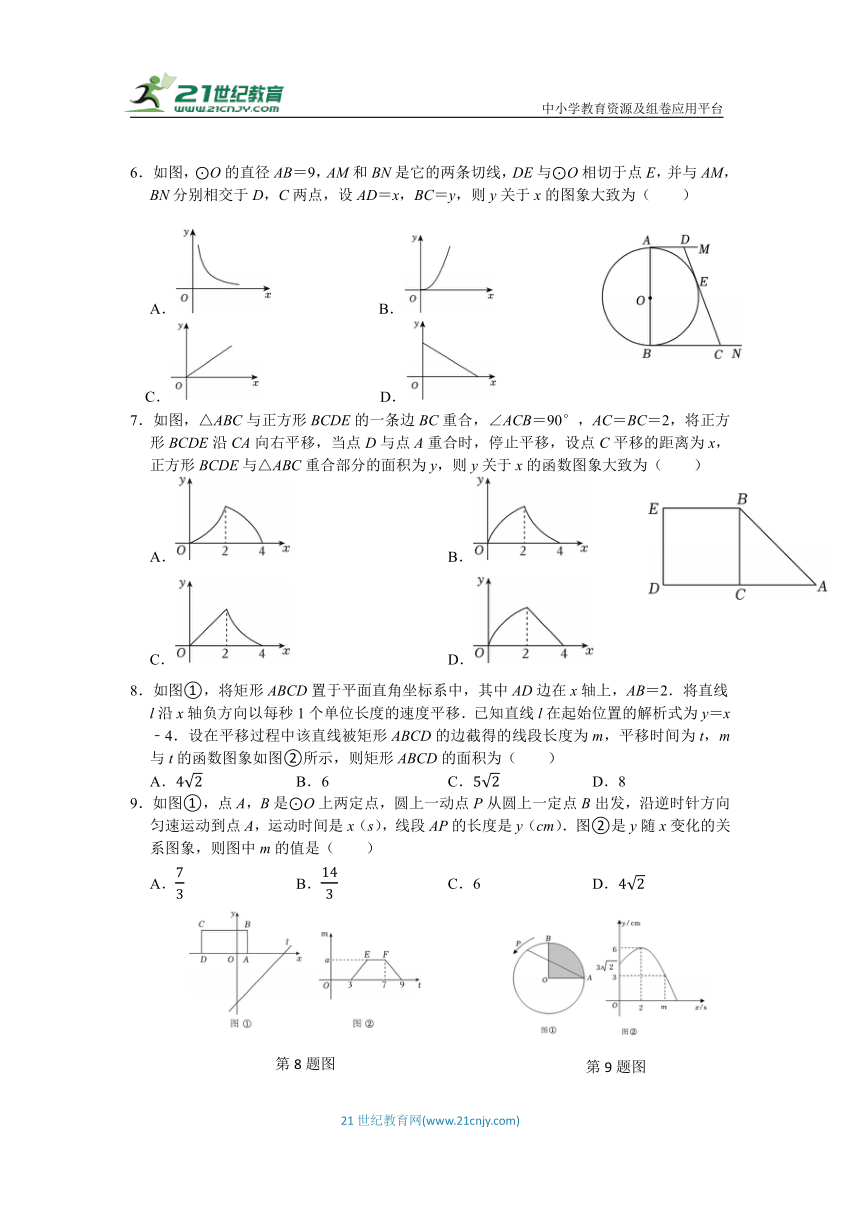
1.如图(1),点M从正方形ABCD的顶点A出发,沿直线运动到正方形ABCD内部一点,再从该点沿直线运动到顶点D,设点M运动的路程为x,点M到线段AD的距离为m,到线段CD的距离为n,且(当点M与D重合时,设y=1),图(2)是点M运动时y随x变化的关系图象,则AB=( )
A. B. C.4 D.
2.如图1,在△ABC中,动点P从点A出发沿折线AB→BC→CA匀速运动至点A后停止.设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的图象,其中点F为曲线DE的最低点,则△ABC的高CG的长度为( )
A.3 B.4 C. D.5
3.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动,如图1所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图2所示,则y的最大值为( )
A.3 B.4 C.5 D.6
4.如图1,在矩形ABCD中,动点P从点B出发,以2cm/s速度沿折线B﹣C﹣D﹣A匀速运动至点A停止.设点P的运动时间为t(s),△PAB的面积为y(m2),y关于t的函数图象如图2所示,则矩形ABCD的对角线长为( )
A. B. C.5cm D.10cm
5.如图,在等腰△ABC中,AC=BC,动点P从点B出发,沿BC→CA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图所示,则AB的值为( )
A. B.5
C. D.3
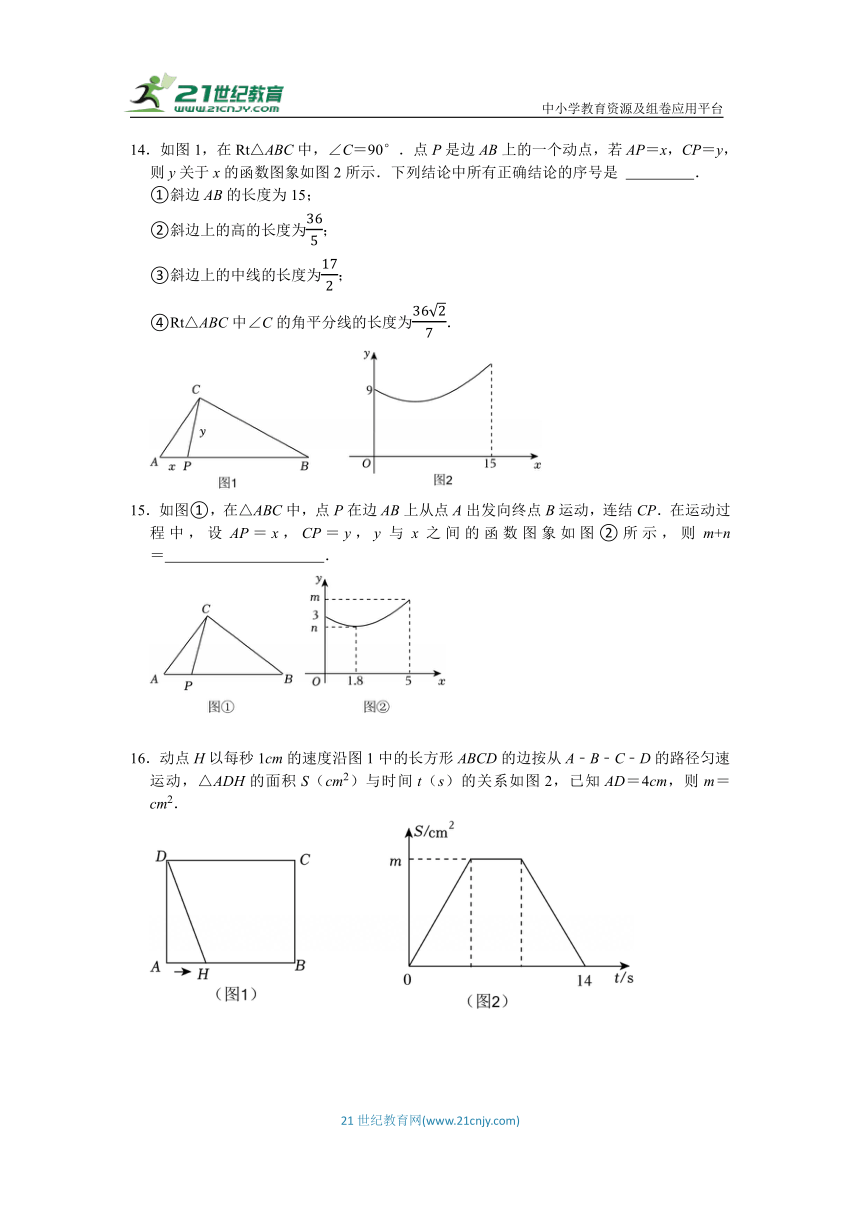
如图,⊙O的直径AB=9,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点,设AD=x,BC=y,则y关于x的图象大致为( )
B.
C. D.
7.如图,△ABC与正方形BCDE的一条边BC重合,∠ACB=90°,AC=BC=2,将正方形BCDE沿CA向右平移,当点D与点A重合时,停止平移,设点C平移的距离为x,正方形BCDE与△ABC重合部分的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
8.如图①,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2.将直线l沿x轴负方向以每秒1个单位长度的速度平移.已知直线l在起始位置的解析式为y=x﹣4.设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图②所示,则矩形ABCD的面积为( )
A. B.6 C. D.8
9.如图①,点A,B是⊙O上两定点,圆上一动点P从圆上一定点B出发,沿逆时针方向匀速运动到点A,运动时间是x(s),线段AP的长度是y(cm).图②是y随x变化的关系图象,则图中m的值是( )
A. B. C.6 D.
10.如图1,在平行四边形ABCD中,BC⊥BD,点F从点B出发,以2cm/s的速度沿B→C→D匀速运动,点E同时从点A出发,以2cm/s的速度沿A→B匀速运动,当其中一个点到达终点时,另一点也随之停止运动,图2是△BEF的面积S(cm2)随时间t(s)变化的函数图象(图中MN为线段),当△BEF的面积为cm2时,运动时间t为( )
A.s B.s或s
C.s D.s
二、填空题
11.如图1,在△ABC中,∠B=60°,点D从点B出发,沿BC向点C运动,速度为1cm/s.过点D作PD⊥BC,交AB边或AC边于点P.当点D运动1s时,点P与点A重合.△PBD的面积S(cm2)与运动时间t(s)之间的关系如图2所示,点E是图象的最高点.当S(cm2)取最大值时,D点的运动时间为 s.
12.如图1,在矩形ABCD中,点P从点A出发,匀速沿AB→BD向点D运动,连接DP,设点P的运动距离为x,DP的长为y,y关于x的函数图象如图2所示,则当点P为AB中点时,DP的长为 .
13.如图,在长方形ABCD中,点P是BC中点,点Q从点P开始,沿着P→B→A→D的路线匀速运动,设△DPQ的面积是y,点Q经过的路线长度为x,如图坐标系中折线表示y与x之间的函数关系,根据图象信息,长方形ABCD的周长为 .
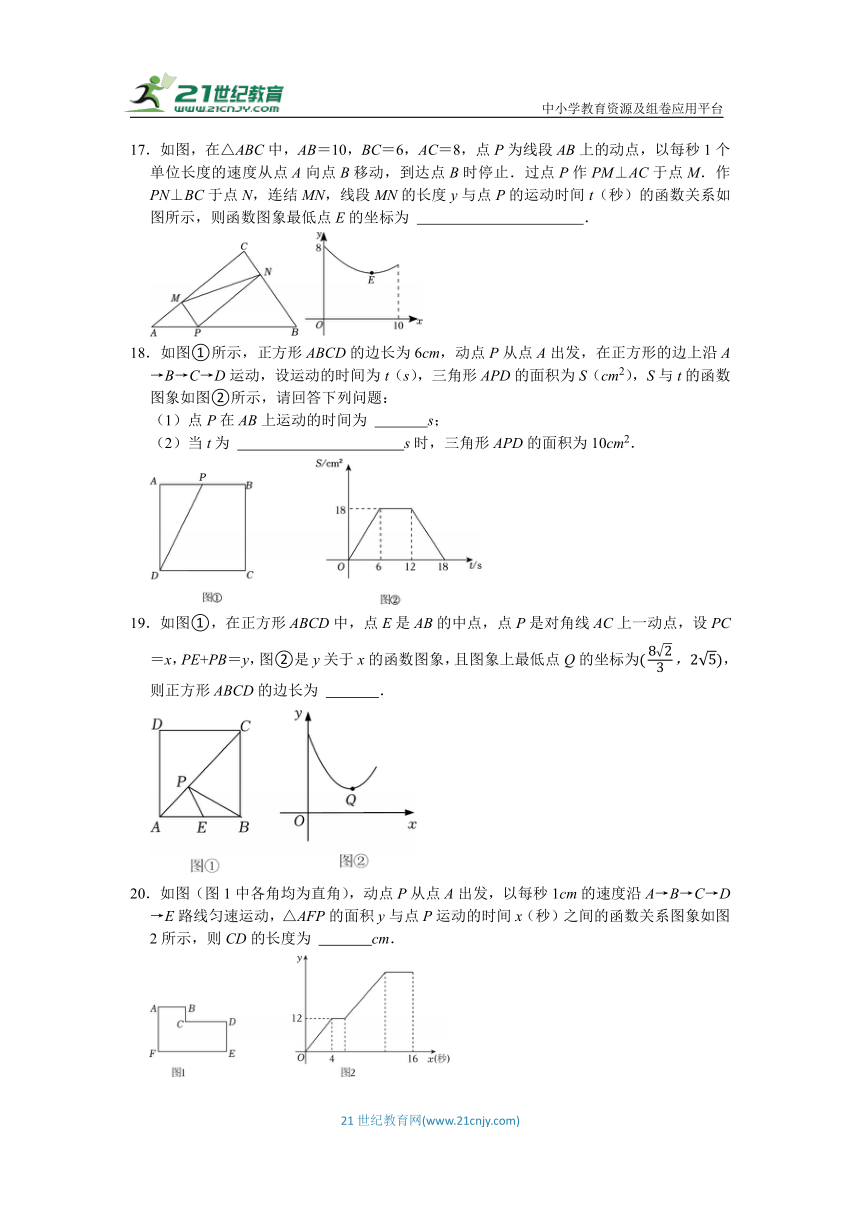
14.如图1,在Rt△ABC中,∠C=90°.点P是边AB上的一个动点,若AP=x,CP=y,则y关于x的函数图象如图2所示.下列结论中所有正确结论的序号是 .
①斜边AB的长度为15;
②斜边上的高的长度为;
③斜边上的中线的长度为;
④Rt△ABC中∠C的角平分线的长度为.
15.如图①,在△ABC中,点P在边AB上从点A出发向终点B运动,连结CP.在运动过程中,设AP=x,CP=y,y与x之间的函数图象如图②所示,则m+n= .
16.动点H以每秒1cm的速度沿图1中的长方形ABCD的边按从A﹣B﹣C﹣D的路径匀速运动,△ADH的面积S(cm2)与时间t(s)的关系如图2,已知AD=4cm,则m= cm2.
17.如图,在△ABC中,AB=10,BC=6,AC=8,点P为线段AB上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作PM⊥AC于点M.作PN⊥BC于点N,连结MN,线段MN的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为 .
18.如图①所示,正方形ABCD的边长为6cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为 s;
(2)当t为 s时,三角形APD的面积为10cm2.
19.如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC=x,PE+PB=y,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形ABCD的边长为 .
20.如图(图1中各角均为直角),动点P从点A出发,以每秒1cm的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y与点P运动的时间x(秒)之间的函数关系图象如图2所示,则CD的长度为 cm.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A D A A B D B C
1.【解答】解:设点N为点M运动的转折点,如图,
结合题图可知,,,DN>AN,点M沿直线DN运动时,,
∴故点N在∠ADC的平分线上,
∴∠ADN=45°,
过点A作AH⊥DN于点H,则AH=DH,DH>HN,
设AH=DH=a,则,
在Rt△AHN中,AH2+HN2=AN2,
∴,
解得:(舍去),,
∴,
∴AB=AD=4,
故选:C.
2.【解答】解:如图过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+BQ=8时,点P到达点Q,此时当P在BC上运动时,AP最小,
∴AB=5,BC=10﹣5=5,BQ=8﹣5=3,
∴QC=2,
∴,
∵,
∴.
故选:B.
3.【解答】解:根据题意得,当x=4时,点P与点C重合,BC=4,AC=7﹣4=3,
∵∠ACB=90°,点D为AB的中点,
∴当x=4时,yS△ABC,
∵S△ABC3×4=3.
∴此时函数有最大值,则y的最大值为3.
故选:A.
4.【解答】解:∵点P以2cm/s速度运动t秒,
∴点P路程为2t cm,
当点P运动到点C处时,t=3,
∴BC=2×3=6(cm),
当点P运动到点D处时,t=7,
∴BC+CD=2×7=14(cm),
∴CD=8cm,
∵四边形ABCD为矩形,
∴AB=CD=8cm,
∴AC10(cm).
故选:D.
5.【解答】解:过A作AD⊥BC于点D,由函数图象可知:AC=BC=5,S△ABC=7.5,
∴∠ADC=∠ADB=90°,
∴,
∴,
∴AD=3,
在直角三角形ACD中,由勾股定理得:,
∴BD=BC﹣CD=5﹣4=1,
在直角三角形ABD中,由勾股定理得:,
故选:A.
6.【解答】解:过D作DF⊥BN交BC于F,
∵AM、BN与⊙O切于点A、B,
∴AB⊥AM,AB⊥BN,
由条件可知∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=9,
∵BC=y,
∴FC=BC﹣BF=y﹣x,
∵DE切⊙O于E,AM、BN与⊙O切于点A、B,
∴DE=DA=x,CE=CB=y,则DC=DE+CE=x+y,
在Rt△DFC中,由勾股定理得:(x+y)2=(y﹣x)2+92,
整理为(x>0),
∴y是x的反比例函数,
故选:A.
7.【解答】解:设点C平移的距离为x,正方形BCDE与△ABC重合部分的面积为y,
∴当0≤x≤2时,如图:
∴;
当2<x≤4时,如图:
∴;
∴,
由分段函数可看出B选项中的函数图象与所求的分段函数对应,
故选:B.
8.【解答】解:由图象可知,当t=3时,m=0,此时直线l平移后过点A,图②中点E时,直线l平移后过点B;点F时,直线l平移后过点D,
当t=9时,m=0,此时直线l平移后过点C,如图①,
∴当t=3时,平移后的解析式为y=x﹣4+3=x﹣1,
令y=0,则x=1,即A(1,0),
当t从7变化到9时,直线l从点D平移到点C,
∴CD=9﹣7=2,
∴直线l从点A平移到点B,t从3变化到5时,
∴BC=9﹣5=4,
∴S矩形ABCD=BC×CD=4×2=8,
故选:D.
9.【解答】解:从图②看,当x=2时,y=AP=6cm,即此时A、O、P三点共线,
则圆的半径为3cm,
当x=0时,OB2+OA2=AP2,
∴△OAB是直角三角形,且OA⊥OB,
则点P从点B走到A、O、P三点共线的位置时(点P与M重合),如图所示,
此时x=2,走过的角度为90°,则走过的弧长为(cm),
∴点P的运动速度是(cm/s),
当t=m时,AP=OA=OB,即△OAP是等边三角形,
∴∠AOP=60°,
∴∠BOP=360°﹣90°﹣60°=210°,
此时点P走过的弧长为:2r(cm),
∴m,
故选:B.
10.【解答】解:由图1、图2可知,当t=4.5时,点F与点C重合;
当4.5<t≤7.5时,点F在CD上运动,而点E继续在AB上运动3s,
∵四边形ABCD是平行四边形,点F、点E的速度都是2cm/s,
∴CD=AB=2×7.5=15(cm),BC=2×4.5=9(cm),
∵BC⊥BD,
∴∠CBD=90°,
∴BD12(cm),
当0<t≤4.5时,如图3,作FG⊥AB,交AB的延长线于点G,则∠G=∠CBD=90°,
∵AB∥CD,
∴∠GBF=∠C,
∴△BGF∽△CBD,
∴,
∴GF BFt(cm),
∴St(15﹣2t)t2+12t,
当S时,则t2+12t,
解得t1=t2s;
当4.5<t≤7.5时,如图4,作CH⊥AB,交AB的延长线于点H,
∵CD CHBC BD=S△CBD,
∴15×CH9×12,
解得CH,
∴S(15﹣2t)t+54,
当S时,则t+54,
解得t,不符合题意,舍去,
综上所述,运动时间t为s;
故选:C.
二、填空题
11.【解答】解:在△ABC中,∠B=60°,点D从点B出发,沿BC向点C运动,速度为1cm/s,当点D运动1s时,点P与点A重合,如图所示,
∴BD=1×1=1(cm),∠BAD=30°,
∴AB=2,
∴AD,
∴,
∴当点P在AB上时,t=1(s)时,△PBD的面积S(cm2)的最大值为,
根据图2可得,t=4(s)时,点D与点C重合,
∴BD=1×4=4(cm),
∴点P与点A重合时,CD=BC﹣BD=3(cm),
在Rt△ACD中,,
∴∠C=30°,
如图所示,当1<t≤4时,点P在AC上,BD=t(cm),CD=BC﹣BD=4﹣t(cm),
∴,
∴,
∴S△PBD(t﹣2)2,
∴当t=2时,△PBD的面积S(cm2)的最大值为,
∵,
∴当S(cm2)取最大值时,D点的运动时间为2s,
故答案为:2.
12.【解答】解:因为P点是从A点出发的,A为初始点,观察图象x=0时y=3,则AD=3,
P从A向B移动的过程中,DP是不断增加的,而P从B向D移动的过程中,DP是不断减少的,
因此转折点为B点,P运动到B点时,即x=a时,AB=a,此时y=a+1,
即BD=a+1,AD=3,AB=a,
在Rt△BAD中,由勾股定理得:AB2+AD2=BD2,
∴a2+32=(a+1)2,
解得a=4,
∴AB=4,
∴当P为AB的中点时,
∴,
故答案为:.
13.【解答】解:由题意得:当点Q从点P运动到点B时,路程为4cm,
∴BP=4cm,
∵点P是BC的中点,
∴BC=2BP=8cm,
∵四边形ABCD是长方形,
∴AD=BC=8cm,
当点Q运动到点A时,△DPQ的面积是24cm2,
∴AB6cm,
∴长方形ABCD的周长为2(8+6)=28(cm).
故答案为:28cm.
14.【解答】解:由图2可知,当x=15时,y取得最大值,即y=CB,
∴斜边AB的长度为15,
故①正确;
由图2可知,当x=0时,y=9,即AC=9,
∴BC12,
∴斜边上的高的长度为:,
故②正确;
∵斜边AB的长度为15,
∴斜边上的中线为,
故③错误;
∵∠C的角平分线是一条直线,
∴不能计算长度,
故④错误;
故答案为:①②.
15.【解答】解:由图2知:当x=0,P和A重合,则AC=3,
当x=1.8时,y最小,最小值为n,此时CP⊥AB,,
∴,
当x=5时,P和B重合,则BC=m,AB=5,
∴,
∴.
故答案为:.
16.【解答】解:观察图2可得:当点H运动到点D时,运动路程为AB+BC+CD,运动时间为14秒,
∵动点H以每秒1cm的速度运动,
∴AB+BC+CD=14cm,
∵AD=4cm,四边形ABCD是矩形,
∴BC=4cm,AB=CD,
∴AB=DC=5cm,
∴当点H运动到点B时,S=m,如图:
∴AD AB=m,
∴m4×5=10.
故答案为:10.
17.【解答】解:连接CP,如图,
∵AB=10,BC=6,AC=8,
∴BC2+AC2=36+64=100,AB2=100,
∴BC2+AC2=AB2,
∴∠ACB=90°.
∵PM⊥AC,PN⊥BC,
∴四边形MPNC为矩形,
∴MN=CP.
∵点P为线段AB上的动点,由于垂线段最短,
∴当CP⊥AB时,CP取得最小值,即y=MN取得最小值.
过点C作CP⊥AB于点P,
∵∠ACB=90°,CP⊥AB,
∴△ACP∽△ABC,
∴,
∴,
∴CP,AP.
∴当t时,y取得最小值为.
∴函数图象最低点E的坐标为(,).
故答案为:(,).
18.【解答】解:(1)由图①、图②可知,当t=6时,点P与点B重合,
∴点P在AB上运动的时间为6s,
故答案为:6.
(2)设点P运动的速度为x cm/s,则6x=6,
∴x=1,
∴点P运动的速度为1cm/s,
当点P在AB边上运动时,则AP=t cm,
∴S6t=3t,
当三角形APD的面积为10cm2时,则S=10,
∴3t=10,
解得t;
当点P在BC边上运动时,三角形APD的面积为6×6=18(cm2),
∴此时不存在三角形APD的面积为10cm2的情况;
当点P在CD边上运动时,则S6(18﹣t)=54﹣3t,
当S=10时,则54﹣3t=10,
解得t,
综上所述,当t为s或s时,三角形APD的面积为10cm2,
故答案为:或.
19.【解答】解:如图,连接DE交AC于点P,
则点D是点B关于直线AC的对称点,
根据点的对称性,PB=PD,则y=PE+PB=PD+PE=DE为最小,
故ED=2,
设正方形的边长为m,则AEm,
在Rt△ADE中,由勾股定理得:DE2=AD2+AE2,
即,
解得:m=4(负值已舍去),
故答案为:4.
20.【解答】解:由图可得,AB=4,S△AFB=12,
∴,即AF=6,
如图,过点C作CG⊥AF,
∵∠A=∠B=∠AGC=90°,∠F=∠E=∠D=90°,
∴四边形ABCG和四边形GFED是矩形,
∴BC=AG,GF=DE,
∴BC+DE=AF=6,
又∵AB+BC+CD+DE=16,
∴CD=6(cm),
故答案为:6.
.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练动点问题的函数图象问题选填题
一、选择题
1.如图(1),点M从正方形ABCD的顶点A出发,沿直线运动到正方形ABCD内部一点,再从该点沿直线运动到顶点D,设点M运动的路程为x,点M到线段AD的距离为m,到线段CD的距离为n,且(当点M与D重合时,设y=1),图(2)是点M运动时y随x变化的关系图象,则AB=( )
A. B. C.4 D.
2.如图1,在△ABC中,动点P从点A出发沿折线AB→BC→CA匀速运动至点A后停止.设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的图象,其中点F为曲线DE的最低点,则△ABC的高CG的长度为( )
A.3 B.4 C. D.5
3.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动,如图1所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图2所示,则y的最大值为( )
A.3 B.4 C.5 D.6
4.如图1,在矩形ABCD中,动点P从点B出发,以2cm/s速度沿折线B﹣C﹣D﹣A匀速运动至点A停止.设点P的运动时间为t(s),△PAB的面积为y(m2),y关于t的函数图象如图2所示,则矩形ABCD的对角线长为( )
A. B. C.5cm D.10cm
5.如图,在等腰△ABC中,AC=BC,动点P从点B出发,沿BC→CA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图所示,则AB的值为( )
A. B.5
C. D.3
如图,⊙O的直径AB=9,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点,设AD=x,BC=y,则y关于x的图象大致为( )
B.
C. D.
7.如图,△ABC与正方形BCDE的一条边BC重合,∠ACB=90°,AC=BC=2,将正方形BCDE沿CA向右平移,当点D与点A重合时,停止平移,设点C平移的距离为x,正方形BCDE与△ABC重合部分的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
8.如图①,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2.将直线l沿x轴负方向以每秒1个单位长度的速度平移.已知直线l在起始位置的解析式为y=x﹣4.设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图②所示,则矩形ABCD的面积为( )
A. B.6 C. D.8
9.如图①,点A,B是⊙O上两定点,圆上一动点P从圆上一定点B出发,沿逆时针方向匀速运动到点A,运动时间是x(s),线段AP的长度是y(cm).图②是y随x变化的关系图象,则图中m的值是( )
A. B. C.6 D.
10.如图1,在平行四边形ABCD中,BC⊥BD,点F从点B出发,以2cm/s的速度沿B→C→D匀速运动,点E同时从点A出发,以2cm/s的速度沿A→B匀速运动,当其中一个点到达终点时,另一点也随之停止运动,图2是△BEF的面积S(cm2)随时间t(s)变化的函数图象(图中MN为线段),当△BEF的面积为cm2时,运动时间t为( )
A.s B.s或s
C.s D.s
二、填空题
11.如图1,在△ABC中,∠B=60°,点D从点B出发,沿BC向点C运动,速度为1cm/s.过点D作PD⊥BC,交AB边或AC边于点P.当点D运动1s时,点P与点A重合.△PBD的面积S(cm2)与运动时间t(s)之间的关系如图2所示,点E是图象的最高点.当S(cm2)取最大值时,D点的运动时间为 s.
12.如图1,在矩形ABCD中,点P从点A出发,匀速沿AB→BD向点D运动,连接DP,设点P的运动距离为x,DP的长为y,y关于x的函数图象如图2所示,则当点P为AB中点时,DP的长为 .
13.如图,在长方形ABCD中,点P是BC中点,点Q从点P开始,沿着P→B→A→D的路线匀速运动,设△DPQ的面积是y,点Q经过的路线长度为x,如图坐标系中折线表示y与x之间的函数关系,根据图象信息,长方形ABCD的周长为 .
14.如图1,在Rt△ABC中,∠C=90°.点P是边AB上的一个动点,若AP=x,CP=y,则y关于x的函数图象如图2所示.下列结论中所有正确结论的序号是 .
①斜边AB的长度为15;
②斜边上的高的长度为;
③斜边上的中线的长度为;
④Rt△ABC中∠C的角平分线的长度为.
15.如图①,在△ABC中,点P在边AB上从点A出发向终点B运动,连结CP.在运动过程中,设AP=x,CP=y,y与x之间的函数图象如图②所示,则m+n= .
16.动点H以每秒1cm的速度沿图1中的长方形ABCD的边按从A﹣B﹣C﹣D的路径匀速运动,△ADH的面积S(cm2)与时间t(s)的关系如图2,已知AD=4cm,则m= cm2.
17.如图,在△ABC中,AB=10,BC=6,AC=8,点P为线段AB上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作PM⊥AC于点M.作PN⊥BC于点N,连结MN,线段MN的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为 .
18.如图①所示,正方形ABCD的边长为6cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为 s;
(2)当t为 s时,三角形APD的面积为10cm2.
19.如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC=x,PE+PB=y,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形ABCD的边长为 .
20.如图(图1中各角均为直角),动点P从点A出发,以每秒1cm的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y与点P运动的时间x(秒)之间的函数关系图象如图2所示,则CD的长度为 cm.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A D A A B D B C
1.【解答】解:设点N为点M运动的转折点,如图,
结合题图可知,,,DN>AN,点M沿直线DN运动时,,
∴故点N在∠ADC的平分线上,
∴∠ADN=45°,
过点A作AH⊥DN于点H,则AH=DH,DH>HN,
设AH=DH=a,则,
在Rt△AHN中,AH2+HN2=AN2,
∴,
解得:(舍去),,
∴,
∴AB=AD=4,
故选:C.
2.【解答】解:如图过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+BQ=8时,点P到达点Q,此时当P在BC上运动时,AP最小,
∴AB=5,BC=10﹣5=5,BQ=8﹣5=3,
∴QC=2,
∴,
∵,
∴.
故选:B.
3.【解答】解:根据题意得,当x=4时,点P与点C重合,BC=4,AC=7﹣4=3,
∵∠ACB=90°,点D为AB的中点,
∴当x=4时,yS△ABC,
∵S△ABC3×4=3.
∴此时函数有最大值,则y的最大值为3.
故选:A.
4.【解答】解:∵点P以2cm/s速度运动t秒,
∴点P路程为2t cm,
当点P运动到点C处时,t=3,
∴BC=2×3=6(cm),
当点P运动到点D处时,t=7,
∴BC+CD=2×7=14(cm),
∴CD=8cm,
∵四边形ABCD为矩形,
∴AB=CD=8cm,
∴AC10(cm).
故选:D.
5.【解答】解:过A作AD⊥BC于点D,由函数图象可知:AC=BC=5,S△ABC=7.5,
∴∠ADC=∠ADB=90°,
∴,
∴,
∴AD=3,
在直角三角形ACD中,由勾股定理得:,
∴BD=BC﹣CD=5﹣4=1,
在直角三角形ABD中,由勾股定理得:,
故选:A.
6.【解答】解:过D作DF⊥BN交BC于F,
∵AM、BN与⊙O切于点A、B,
∴AB⊥AM,AB⊥BN,
由条件可知∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=9,
∵BC=y,
∴FC=BC﹣BF=y﹣x,
∵DE切⊙O于E,AM、BN与⊙O切于点A、B,
∴DE=DA=x,CE=CB=y,则DC=DE+CE=x+y,
在Rt△DFC中,由勾股定理得:(x+y)2=(y﹣x)2+92,
整理为(x>0),
∴y是x的反比例函数,
故选:A.
7.【解答】解:设点C平移的距离为x,正方形BCDE与△ABC重合部分的面积为y,
∴当0≤x≤2时,如图:
∴;
当2<x≤4时,如图:
∴;
∴,
由分段函数可看出B选项中的函数图象与所求的分段函数对应,
故选:B.
8.【解答】解:由图象可知,当t=3时,m=0,此时直线l平移后过点A,图②中点E时,直线l平移后过点B;点F时,直线l平移后过点D,
当t=9时,m=0,此时直线l平移后过点C,如图①,
∴当t=3时,平移后的解析式为y=x﹣4+3=x﹣1,
令y=0,则x=1,即A(1,0),
当t从7变化到9时,直线l从点D平移到点C,
∴CD=9﹣7=2,
∴直线l从点A平移到点B,t从3变化到5时,
∴BC=9﹣5=4,
∴S矩形ABCD=BC×CD=4×2=8,
故选:D.
9.【解答】解:从图②看,当x=2时,y=AP=6cm,即此时A、O、P三点共线,
则圆的半径为3cm,
当x=0时,OB2+OA2=AP2,
∴△OAB是直角三角形,且OA⊥OB,
则点P从点B走到A、O、P三点共线的位置时(点P与M重合),如图所示,
此时x=2,走过的角度为90°,则走过的弧长为(cm),
∴点P的运动速度是(cm/s),
当t=m时,AP=OA=OB,即△OAP是等边三角形,
∴∠AOP=60°,
∴∠BOP=360°﹣90°﹣60°=210°,
此时点P走过的弧长为:2r(cm),
∴m,
故选:B.
10.【解答】解:由图1、图2可知,当t=4.5时,点F与点C重合;
当4.5<t≤7.5时,点F在CD上运动,而点E继续在AB上运动3s,
∵四边形ABCD是平行四边形,点F、点E的速度都是2cm/s,
∴CD=AB=2×7.5=15(cm),BC=2×4.5=9(cm),
∵BC⊥BD,
∴∠CBD=90°,
∴BD12(cm),
当0<t≤4.5时,如图3,作FG⊥AB,交AB的延长线于点G,则∠G=∠CBD=90°,
∵AB∥CD,
∴∠GBF=∠C,
∴△BGF∽△CBD,
∴,
∴GF BFt(cm),
∴St(15﹣2t)t2+12t,
当S时,则t2+12t,
解得t1=t2s;
当4.5<t≤7.5时,如图4,作CH⊥AB,交AB的延长线于点H,
∵CD CHBC BD=S△CBD,
∴15×CH9×12,
解得CH,
∴S(15﹣2t)t+54,
当S时,则t+54,
解得t,不符合题意,舍去,
综上所述,运动时间t为s;
故选:C.
二、填空题
11.【解答】解:在△ABC中,∠B=60°,点D从点B出发,沿BC向点C运动,速度为1cm/s,当点D运动1s时,点P与点A重合,如图所示,
∴BD=1×1=1(cm),∠BAD=30°,
∴AB=2,
∴AD,
∴,
∴当点P在AB上时,t=1(s)时,△PBD的面积S(cm2)的最大值为,
根据图2可得,t=4(s)时,点D与点C重合,
∴BD=1×4=4(cm),
∴点P与点A重合时,CD=BC﹣BD=3(cm),
在Rt△ACD中,,
∴∠C=30°,
如图所示,当1<t≤4时,点P在AC上,BD=t(cm),CD=BC﹣BD=4﹣t(cm),
∴,
∴,
∴S△PBD(t﹣2)2,
∴当t=2时,△PBD的面积S(cm2)的最大值为,
∵,
∴当S(cm2)取最大值时,D点的运动时间为2s,
故答案为:2.
12.【解答】解:因为P点是从A点出发的,A为初始点,观察图象x=0时y=3,则AD=3,
P从A向B移动的过程中,DP是不断增加的,而P从B向D移动的过程中,DP是不断减少的,
因此转折点为B点,P运动到B点时,即x=a时,AB=a,此时y=a+1,
即BD=a+1,AD=3,AB=a,
在Rt△BAD中,由勾股定理得:AB2+AD2=BD2,
∴a2+32=(a+1)2,
解得a=4,
∴AB=4,
∴当P为AB的中点时,
∴,
故答案为:.
13.【解答】解:由题意得:当点Q从点P运动到点B时,路程为4cm,
∴BP=4cm,
∵点P是BC的中点,
∴BC=2BP=8cm,
∵四边形ABCD是长方形,
∴AD=BC=8cm,
当点Q运动到点A时,△DPQ的面积是24cm2,
∴AB6cm,
∴长方形ABCD的周长为2(8+6)=28(cm).
故答案为:28cm.
14.【解答】解:由图2可知,当x=15时,y取得最大值,即y=CB,
∴斜边AB的长度为15,
故①正确;
由图2可知,当x=0时,y=9,即AC=9,
∴BC12,
∴斜边上的高的长度为:,
故②正确;
∵斜边AB的长度为15,
∴斜边上的中线为,
故③错误;
∵∠C的角平分线是一条直线,
∴不能计算长度,
故④错误;
故答案为:①②.
15.【解答】解:由图2知:当x=0,P和A重合,则AC=3,
当x=1.8时,y最小,最小值为n,此时CP⊥AB,,
∴,
当x=5时,P和B重合,则BC=m,AB=5,
∴,
∴.
故答案为:.
16.【解答】解:观察图2可得:当点H运动到点D时,运动路程为AB+BC+CD,运动时间为14秒,
∵动点H以每秒1cm的速度运动,
∴AB+BC+CD=14cm,
∵AD=4cm,四边形ABCD是矩形,
∴BC=4cm,AB=CD,
∴AB=DC=5cm,
∴当点H运动到点B时,S=m,如图:
∴AD AB=m,
∴m4×5=10.
故答案为:10.
17.【解答】解:连接CP,如图,
∵AB=10,BC=6,AC=8,
∴BC2+AC2=36+64=100,AB2=100,
∴BC2+AC2=AB2,
∴∠ACB=90°.
∵PM⊥AC,PN⊥BC,
∴四边形MPNC为矩形,
∴MN=CP.
∵点P为线段AB上的动点,由于垂线段最短,
∴当CP⊥AB时,CP取得最小值,即y=MN取得最小值.
过点C作CP⊥AB于点P,
∵∠ACB=90°,CP⊥AB,
∴△ACP∽△ABC,
∴,
∴,
∴CP,AP.
∴当t时,y取得最小值为.
∴函数图象最低点E的坐标为(,).
故答案为:(,).
18.【解答】解:(1)由图①、图②可知,当t=6时,点P与点B重合,
∴点P在AB上运动的时间为6s,
故答案为:6.
(2)设点P运动的速度为x cm/s,则6x=6,
∴x=1,
∴点P运动的速度为1cm/s,
当点P在AB边上运动时,则AP=t cm,
∴S6t=3t,
当三角形APD的面积为10cm2时,则S=10,
∴3t=10,
解得t;
当点P在BC边上运动时,三角形APD的面积为6×6=18(cm2),
∴此时不存在三角形APD的面积为10cm2的情况;
当点P在CD边上运动时,则S6(18﹣t)=54﹣3t,
当S=10时,则54﹣3t=10,
解得t,
综上所述,当t为s或s时,三角形APD的面积为10cm2,
故答案为:或.
19.【解答】解:如图,连接DE交AC于点P,
则点D是点B关于直线AC的对称点,
根据点的对称性,PB=PD,则y=PE+PB=PD+PE=DE为最小,
故ED=2,
设正方形的边长为m,则AEm,
在Rt△ADE中,由勾股定理得:DE2=AD2+AE2,
即,
解得:m=4(负值已舍去),
故答案为:4.
20.【解答】解:由图可得,AB=4,S△AFB=12,
∴,即AF=6,
如图,过点C作CG⊥AF,
∵∠A=∠B=∠AGC=90°,∠F=∠E=∠D=90°,
∴四边形ABCG和四边形GFED是矩形,
∴BC=AG,GF=DE,
∴BC+DE=AF=6,
又∵AB+BC+CD+DE=16,
∴CD=6(cm),
故答案为:6.
.
21世纪教育网(www.21cnjy.com)
同课章节目录
