2025年九年级数学中考三轮冲刺训练一次函数的应用—行程信息问题(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练一次函数的应用—行程信息问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 19:37:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练一次函数的应用—行程信息问题
一、选择题
1.在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.客车、货车离C站的路程y1,y2(km)与行驶时间x(h)之间的函数图象如图所示.有下列说法:①A,B两地相距为420km;②两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=30x﹣60;③客车离C站的路程y1与行驶时间x之间的函数关系式为:y1=﹣60x+360;④客、货两车在小时相遇.其中正确的个数有( )
A.4 B.3 C.2 D.1
2.如图,甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后1.5小时追上甲车;
④当乙追上甲后,甲乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列说法错误的是( )
A.乙用12分钟追上甲
B.乙追上甲后,再走1440米才到达
C.甲乙两人之间的最远距离是300米
D.甲到终点时,乙已经在终点处休息了6分钟
4.人工智能的发展使得智能机器人送餐成为时尚.如图,某餐厅的机器人小数和小文从厨房门口出发,准备给相距450cm的客人送餐,小数比小文先出发,且速度保持不变,小文出发一段时间后将速度提高到原来的2倍.设小数行走的时间为x(s),小数和小文行走的路程分别为y1(cm),y2(cm),y1,y2与x之间的函数图象如图所示,则下列说法不正确的是( )
A.小数比小文先出发15秒
B.小文提速后的速度为30cm/s
C.n=40
D.从小数出发至送餐结束,小文和小数最远相距150cm
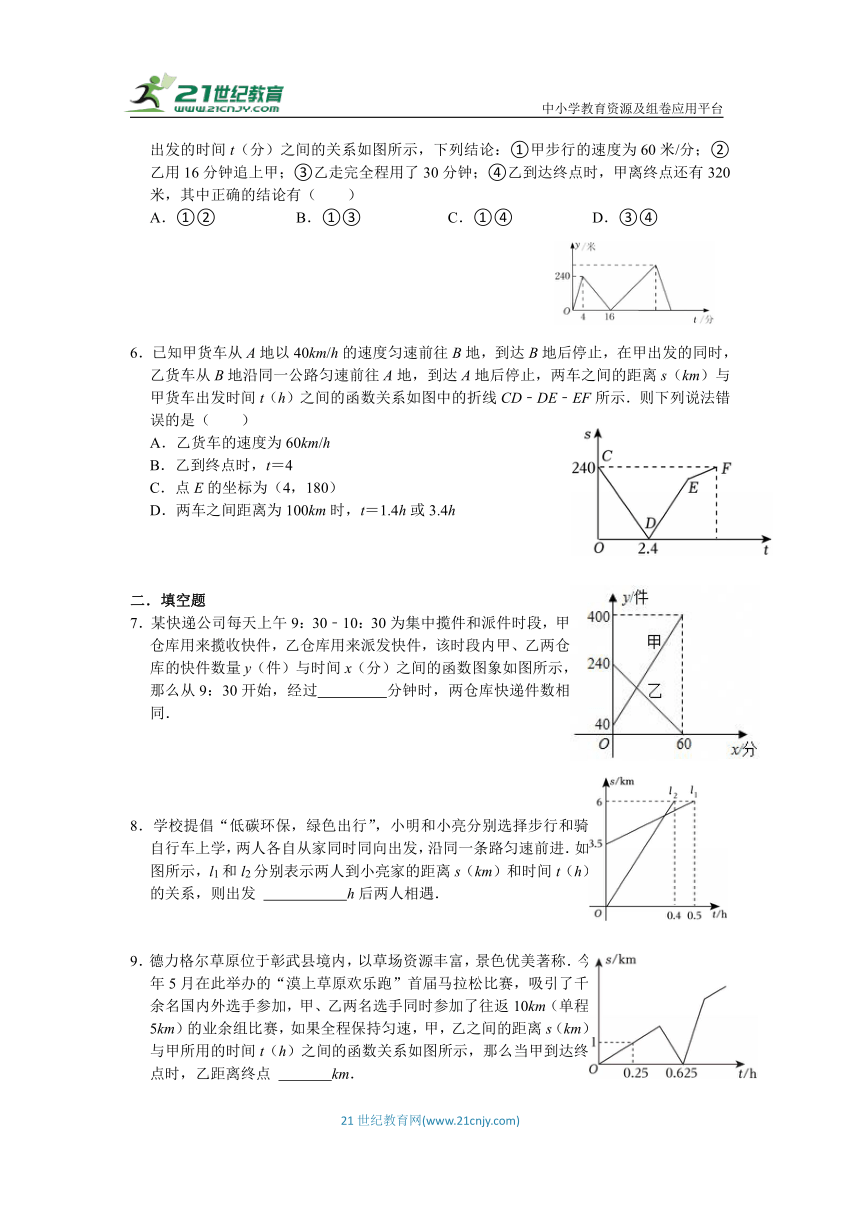
5.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时,甲离终点还有320米,其中正确的结论有( )
A.①② B.①③ C.①④ D.③④
6.已知甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的距离s(km)与甲货车出发时间t(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.则下列说法错误的是( )
A.乙货车的速度为60km/h
B.乙到终点时,t=4
C.点E的坐标为(4,180)
D.两车之间距离为100km时,t=1.4h或3.4h
二.填空题
7.某快递公司每天上午9:30﹣10:30为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么从9:30开始,经过 分钟时,两仓库快递件数相同.
8.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进.如图所示,l1和l2分别表示两人到小亮家的距离s(km)和时间t(h)的关系,则出发 h后两人相遇.
9.德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加,甲、乙两名选手同时参加了往返10km(单程5km)的业余组比赛,如果全程保持匀速,甲,乙之间的距离s(km)与甲所用的时间t(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 km.
10.快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离s(km)与行驶时间t(h)之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 km/h.
三.解答题
11.大运河畔有一条笔直的健身步道,小明、小亮分别从相距1500米的M、N两点同时出发,相向而行.两人离M点的距离s关于时间t的函数关系如图中折线所示.小明跑了一段路之后与小亮相距250米,休息1分钟之后与小亮相距400米,小明继续跑了4分钟后与小亮同时到达各自终点.
(1)a的值为 ;
(2)求图中BC所对应的函数表达式;
(3)求小明、小亮相遇的时间.
12.一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早小时到达目的地.甲、乙两车之间的路程y km与两车行驶时间x h的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
13.领航无人机表演团队进行无人机表演训练,甲无人机以a米/秒的速度从地面起飞,乙无人机从距离地面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙无人机按照训练计划准时到达距离地面的高度为96米时,进行了时长为t秒的联合表演,表演完成后以相同的速度大小同时返回地面.甲、乙两架无人机所在的位置距离地面的高度y(米)与无人机飞行的时间x(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)a= 米/秒,t= 秒;
(2)求线段MN所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米?(直接写出答案即可)
14.一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地,小时后,一辆货车从A地出发,沿同一路线每小时行驶80千米匀速驶向B地,货车到达B地填装货物耗时15分钟,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是 千米,a= ;
(2)求线段FG所在直线的函数解析式;
(3)货车出发多少小时两车相距15千米?(直接写出答案即可)
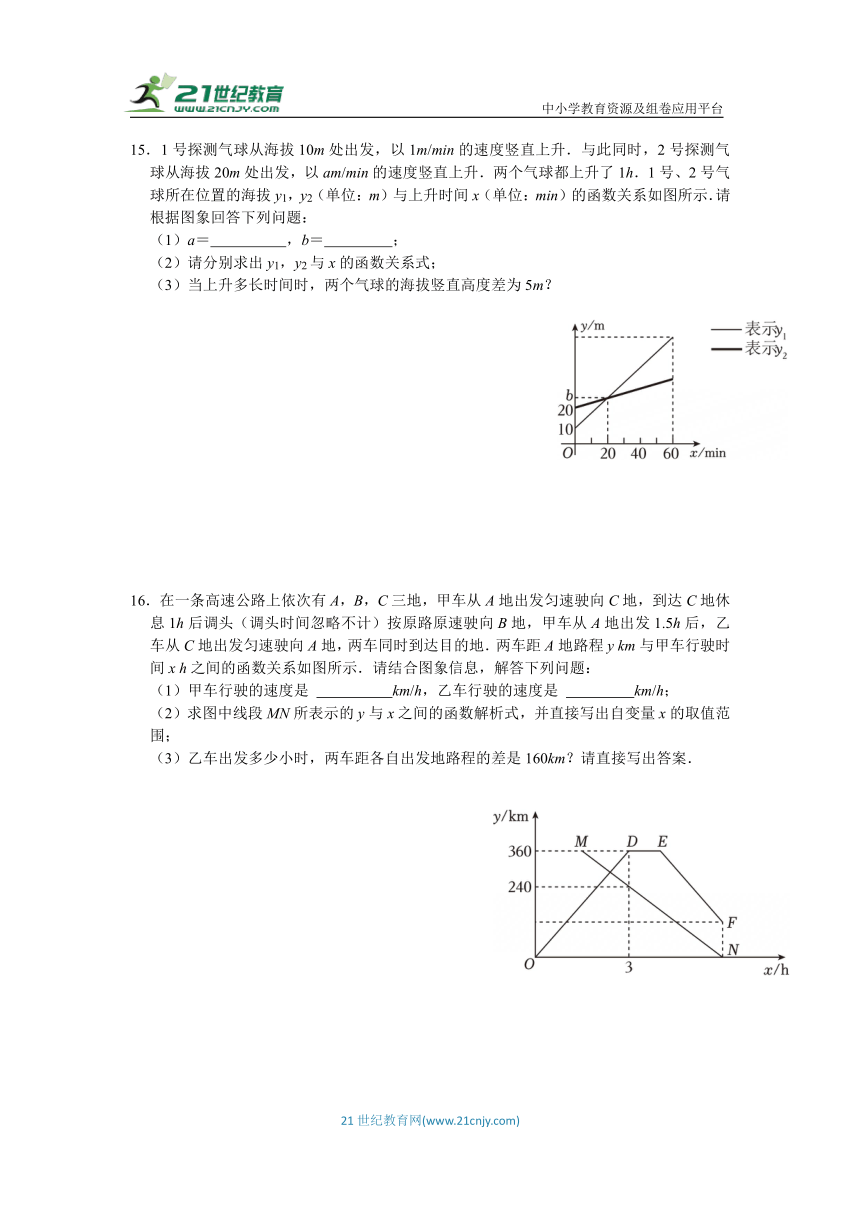
15.1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.两个气球都上升了1h.1号、2号气球所在位置的海拔y1,y2(单位:m)与上升时间x(单位:min)的函数关系如图所示.请根据图象回答下列问题:
(1)a= ,b= ;
(2)请分别求出y1,y2与x的函数关系式;
(3)当上升多长时间时,两个气球的海拔竖直高度差为5m?
16.在一条高速公路上依次有A,B,C三地,甲车从A地出发匀速驶向C地,到达C地休息1h后调头(调头时间忽略不计)按原路原速驶向B地,甲车从A地出发1.5h后,乙车从C地出发匀速驶向A地,两车同时到达目的地.两车距A地路程y km与甲车行驶时间x h之间的函数关系如图所示.请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,乙车行驶的速度是 km/h;
(2)求图中线段MN所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时,两车距各自出发地路程的差是160km?请直接写出答案.
17.已知甲,乙两地相距480km,一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车继续出发h后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是 ;
(2)求货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数关系式;
(3)直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距12km.
18.已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
(1)m= ,n= ;
(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的路程.
19.在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米?(直接写出答案即可)
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 A D C C B C
1.【解答】解:由图象可得:A,B两地相距为360+60=420(km),故①正确;
货车的速度为:60÷2=30(km/h),
故货车到达A地一共需要2+360÷30=14(h),
设两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=kx+b,
由题意可得:,
解得:,
∴y2=30x﹣60,故②正确;
设客车离C站的路程y1与行驶时间x之间的函数关系式为y=mx+n,
由题意可得:,
解得,
∴y1=﹣60x+360,故③正确;
由y1=y2得﹣60x+360=30x﹣60,
解得:,
∵,
∴符合题意,即客、货两车在小时相遇,故④正确;
故选:A.
2.【解答】解:图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③正确;
当乙追上甲后,令y乙﹣y甲=50,100t﹣100﹣60t=50
解得,
当乙到达目的地,甲自己行走时,y甲=60t=250,
解得,
∴综上所述,当乙追上甲后,甲乙两车相距50千米时,或.故④正确;
综上可知正确的有①②③④,共4个.
故选:D.
3.【解答】解:16﹣4=12(分),
∴乙用12分钟追上甲,
∴A正确,不符合题意;
甲的速度为240÷4=60(米/分),
乙追上甲时,二人离起点的距离为2400﹣60×16=1440(米),
∴乙追上甲后,再走1440米才到达,
∴B正确,不符合题意;
乙的速度为60×16÷(16﹣4)=80(米/分),
乙到达终点所用的时间为2400÷80=30(分),
当乙到达终点时甲走的路程为60×(30+4)=2040(米),
当乙到达终点时,甲、乙二人的距离最远,为2400﹣2040=360(米),
∴C错误,符合题意;
∵当乙到达终点时甲走的路程为2040米,
∴甲还需要(2400﹣2040)÷60=6(分)到达终点,
∴甲到终点时,乙已经在终点处休息了6分钟,
∴D正确,不符合题意.
故选:C.
4.【解答】解:根据图象,小数比小文先出发15秒,
∴A正确,不符合题意;
小文提速前的速度为30÷(17﹣15)=15(cm/s),
∴小文提速后的速度为15×2=30(cm/s),
∴B正确,不符合题意;
∵30(m﹣17)=450﹣30,
∴m=31,
∴小数的速度为310÷31=10(cm/s),
∴小数到达目的地所用时间为450÷10=45(s),
∴n=45,
∴C不正确,符合题意;
小数和小文相遇前,当x=15时小文和小数相距最远,为10×15=150(cm),
小数和小文相遇后,当x=m=31时小文和小数相距最远,为450﹣10×31=140(cm),
∵150>140,
∴从小数出发至送餐结束,小文和小数最远相距150cm,
∴D正确,不符合题意.
故选:C.
5.【解答】解:甲步行的速度为240÷4=60(米/分),
∴①正确,符合题意;
乙用16﹣4=12(分)追上甲,
∴②不正确,不符合题意;
设乙的速度为v米/分,则12(v﹣60)=240,
解得v=80,
则乙走完全程用了2400÷80=30(分),
∴③正确,符合题意;
乙到达终点时,甲离终点还有2400﹣60×(30+4)=360(米),
∴④不正确,不符合题意.
综上,①③正确.
故选:B.
6.【解答】解:设乙货车的速度为v km/h,则2.4(40+v)=240,
解得v=60,
∴乙货车的速度为60km/h,
∴A正确,不符合题意;
乙到终点时所用时间为240÷60=4(h),
∴B正确,不符合题意;
根据②,当乙到达终点时,甲距离A地40×4=160(km),
∴当乙到终点时,甲乙相距160km,
点E的坐标为(4,160),
∴C不正确,符合题意;
设线段CD对应的函数关系式为s=k1t+b1(k1、b1为常数,且k1≠0),
将坐标C(0,240)和D(2.4,0)分别代入s=k1t+b1,
得,
解得,
∴线段CD对应的函数关系式为s=﹣100t+240(0≤t≤2.4),
当s=100时,得﹣100t+240=100,
解得t=1.4;
设线段DE对应的函数关系式为s=k2t+b2(k2、b2为常数,且k2≠0),
将坐标D(2.4,0)和E(4,160)分别代入s=k2t+b2,
得,
解得,
∴线段DE对应的函数关系式为s=100t﹣240,
当s=100时,得100t﹣240=100,
解得t=3.4,
∴当t=1.4h或3.4h时,两车之间距离为100km,
∴D正确,不符合题意.
故选:C.
二、填空题
7.【解答】解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=﹣4,
∴y2=﹣4x+240,
联立,
解得,
∴经过20分钟时,当两仓库快递件数相同.
故答案为:20
8.【解答】解:设l1的函数解析式为y1=kx+b,
则,
解得,
∴l1的函数解析式为S1=5t+3.5;
设l2的函数解析式为S2=mt,
则0.4m=6,
解得m=15,
∴l2的函数解析式为S2=15t;
令S1=S2,即5t+3.5=15t,
解得t=0.35,
∴出发0.35小时后两人相遇.
故答案为:0.35.
9.【解答】解:设甲的速度为x千米/小时,则乙的速度为(x﹣4)千米/小时,
则:[(x﹣4)+x]=10,
解得:x=10,
乙的速度为 10﹣4=6km/h,甲到终点的时间为:10÷10=1h,
此时,乙走过的路程为:1×6=6km,
所以,乙距离终点:10﹣6=4km.
10.【解答】解:∵快递员始终匀速行驶,
∴快递员的行驶速度是35(km/h).
故答案为:35.
三、解答题
11.【解答】解:(1)由题意可知,小亮的速度是400﹣250=150(m/min),
1500÷150=10(min),
∴a=10.
故答案为:10.
(2)10﹣4=6(min),
6min时小亮与N点的距离为150×6=900(m),则此时小明与M点的距离为1500﹣900+400=1000(m),
∴B(6,1000).
设BC所对应的函数表达式为s=kt+b(k、b为常数,且k≠0),
将B(6,1000)和C(10,1500)分别代入s=kt+b,
得,
解得,
∴BC所对应的函数表达式为s=125t+250(6≤t≤10).
(3)∵B(6,1000),
∴A(5,1000),
∴小明的速度为1000÷5=200(m/min),
1500÷(200+150)(min).
答:小明、小亮相遇的时间为min.
12.【解答】解:(1)由图可知,甲车小时行驶的路程为(200﹣180)km,
∴甲车行驶的速度是,
70×(4)=300(km),
填图如下:
故答案为:70;
(2)由图可知E,F的坐标分别为,(4,180),
设线段EF所在直线的函数解析式为y=kx+b,
则,
解得,
∴线段EF所在直线的函数解析式为y=120x﹣300;
(3)由题意知,A、C两地的距离为:,
乙车行驶的速度为:,
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300﹣200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况:
甲在AB之间时:
200﹣50x=3(100﹣70x),
解得;
甲在BC之间时:
200﹣50x=3(70x﹣100),
解得;
综上可知,两车出发或时,乙车距B地的路程是甲车距B地路程的3倍.
13.【解答】解:(1)由题意得甲无人机的速度为 a=48÷6=8(米/秒),
t=39﹣19=20(秒).
故答案为:8,20;
(2)由图象知,N(19,96),
∵甲无人机的速度为8米/秒,
∴甲无人机匀速从0米到96米所用时间为96÷8=12(秒),
∴甲无人机单独表演所用时间为19﹣12=7(秒),
6+7=13(秒),
∴M(13,48),
设线段MN所在直线的函数解析式为y=kx+b,
将M(13,48),N(19,96)代入得
,
解得
∴线段MN所在直线的函数解析式为y=8x﹣56.
(3)由题意A(0,20),B(6,48),
同理线段OB所在直线的函数解析式为y=8x,
线段AN所在直线的函数解析式为y=4x+20,
线段BM所在直线的函数解析式为y=48,
当0≤x≤6时,由题意得|4x+20﹣8x|=12,
解得x=2或x=8(舍去),
当6<x≤13时,由题意得|4x+20﹣48|=12,
解得x=10或x=4(舍去),
当13<x≤19时,由题意得|8x﹣56﹣4x﹣20|=12,
解得x=16或x=22(舍去),
综上,两架无人机表演训练到2秒或10秒或16秒时,它们距离地面的高度差为12米.
14.【解答】解:(1)∵8060(千米),
∴A,B两地之间的距离是60千米;
∵货车到达B地填装货物耗时15分钟,
∴a1,
故答案为:60,1;
(2)设线段FG所在直线的解析式为y=kx+b(k≠0),将F(1,60),G(2,0)代入得:
,
解得 ,
∴线段FG所在直线的函数解析式为y=﹣60x+120;
(3)巡逻车速度为60÷(2)=25(千米/小时),
∴线段CD的解析式为y=25x+2525x+10(0≤x≤2),
当货车第一次追上巡逻车后,80x﹣(25x+10)=15,
解得x;
当货车返回与巡逻车未相遇时,(﹣60x+120)﹣(25x+10)=15,
解得x;
当货车返回与巡逻车相遇后,(25x+10)﹣(﹣60x+120)=15,
解得x;
综上所述,货车出发小时或 小时或小时,两车相距15千米.
15.【解答】解:(1)∵1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.
当x=20时,两球相遇,
y1=10+x=10+20=30,
∴b=30,
设2号探测气球解析式为y2=20+ax,
∵y2=20+ax过(20,30),
∴30=20+20a,
解得a=0.5,
∴y2=20+0.5x,
故答案为:0.5,30;
(2)根据题意得:
1号探测气球所在位置的海拔:y1=10+x,
2号探测气球所在位置的海拔:y2=20+0.5x;
(3)分两种情况:
①2号探测气球比1号探测气球海拔高5米,根据题意得:
(20+0.5x)﹣(x+10)=5,
解得x=10;
②1号探测气球比2号探测气球海拔高5米,根据题意得:
(x+10)﹣(0.5x+20)=5,
解得x=30.
综上所述,上升了10或30min后这两个气球相距5m.
16.【解答】解:(1)由图可得D(3,360),即甲出发3时后与A地相距360km,
∴甲车行驶速度为120(km/h),
由题意可得,乙车出发1.5h行驶120km,
∴乙车行驶速度为 80(km/h),
故答案为:120,80;
(2)设线段MN所在直线的解析式为 y=kx+b(k≠0),
将(1.5,360),(3,240)代入y=kx+b,
得,
解得,
∴线段MN所在直线的解析式为y=﹣80x+480(1.5≤x≤6);
(3)由题意可得,当y=0时,x=6,
∴N(6,0),
∵两车同时到达目的地,
∴乙到达目的地时,甲距离A地的距离为360﹣120×(6﹣3﹣1)=120(km),
∴F(6,120),E(4,360),
设乙车出发t时,两车距各自出发地路程的差是160km,
当0<t≤1.5时,此时甲在到达C地前,则|80t﹣120×(t+1.5)|=160,
解得t为负数,不合题意;
当1.5<t≤2.5时,此时甲在C地休息,则|80t﹣360|=160,
解得t1=2.5,t2=6.5(不合题意,舍去);
当2.5<t≤4.5时,此时甲掉头驶向B地,则|80t﹣[2×360﹣120×(t+1.5﹣1)]|=160,
解得t1=2.5(不合题意,舍去),t2=4.1;
综上,乙车出发2.5h或4.1h,两车距各自出发地路程的差是160km.
17.【解答】解:(1)由图象知,C(4,480),
设直线OC的解析式为y=kx,把C(4,480)代入得,480=4k,
解得k=120,
∴直线OC的解析式为y=120x;把(1,a)代入y=120x,得a=120,
故答案为:120;
(2)由停下来装完货物后,发现此时与出租车相距120km,货车行驶时间为小时,
∵a=120(km),
∴货车卸货时与乙地相距120km,
∴出租车距离乙地为120+120=240(km),
∴出租车距离甲地为480﹣240=240(km),
把y=240代入y=120x得,240=120x,
解得x=2,
∴货车装完货物时,x=2,B(2,120),
根据货车继续出发h后与出租车相遇,
可得(出租车的速度+货车的速度)=120,
根据直线OC的解析式为y=120x(0≤x≤4),
可得出租车的速度为120km/h,
∴相遇时,货车的速度为120120=60(km/h),
故可设直线BG的解析式为y=60x+b,
将B(2,120)代入y=60x+b,可得120=120+b,
解得b=0,
∴直线BG的解析式为y=60x(2≤x≤8),
故货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数关系式为y=60x,
(3)把y=480代入y=60x,可得480=60x,
解得x=8,
∴G(8,480),
∴F(8,0),
根据出租车到达乙地后立即按原路返回,经过比货车早15分钟到达甲地,可得EF,
∴,
∴出租车返回后的速度为480÷()=128km/h,
设在出租车返回的行驶过程中,货车出发t小时,与出租车相距12km,
此时货车距离乙地为60t km,出租车距离乙地为128(t﹣4)=(128t﹣512)km,
①出租车和货车第二次相遇前,相距12km时,可得60t1﹣(128t1﹣512)=12,
解得t1;
②出租车和货车第二次相遇后,相距12km时,可得(128t2﹣512)﹣60t2=12,
解得t2,
故在出租车返回的行驶过程中,货车出发h或h与出租车相距12km.
18.【解答】解:(1)由题意知:m=200÷100=2,
n=m+4=2+4=6,
故答案为:2,6;
(2)设y=kx+b,将(2,200),(6,440)代入得:
,
解得,
∴y=60x+80,(2≤x≤6);
(3)乙车的速度为(440﹣200)÷2=120(千米/小时),
∴乙车到达A地所需时间为440÷120(小时),
当x时,y=6080=300,
∴甲车距A地的路程为300千米.
19.【解答】解:(1)由图象知:当x=0时,y=1200,
∴A、B两地之间的距离是1200米;
由图象知:乙经过20分钟到达A,
∴乙的速度为60(米/分).
故答案为:1200;60;
(2)由图象知:当x时,y=0,
∴甲乙二人的速度和为:1200140(米/分),
设甲的速度为x米/分,则乙的速度为(140﹣x)米/分,
∴140﹣x==60,
∴x=80.
∴甲的速度为80(米/分),
∵点M的实际意义是经过c分钟甲到达B地,
∴c=1200÷80=15(分钟),
∴a=60×15=900(米).
∵点N的实际意义是经过20分钟乙到达A地,
∴b=900﹣(80﹣60)×5=800(米);
故答案为:900;800;15;
(3)由题意得:M(15,900),N(20,800),
设线段MN的解析式为y=kx+n,
∴,
解得:,
∴线段MN的解析式为y=﹣20x+1200(15≤x≤20);
(4)在乙运动的过程中,二人出发后第8分钟和第分钟两人相距80米.理由:
①相遇前两人相距80米时,二人的所走路程和为1200﹣80=1120(米),
∴1120÷140=8(分钟);
②相遇后两人相距80米时,二人的所走路程和为1200+80=1280(米),
∴1280÷140(分钟).
综上,在乙运动的过程中,二人出发后第8分钟和第分钟两人相距80米.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练一次函数的应用—行程信息问题
一、选择题
1.在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.客车、货车离C站的路程y1,y2(km)与行驶时间x(h)之间的函数图象如图所示.有下列说法:①A,B两地相距为420km;②两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=30x﹣60;③客车离C站的路程y1与行驶时间x之间的函数关系式为:y1=﹣60x+360;④客、货两车在小时相遇.其中正确的个数有( )
A.4 B.3 C.2 D.1
2.如图,甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后1.5小时追上甲车;
④当乙追上甲后,甲乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列说法错误的是( )
A.乙用12分钟追上甲
B.乙追上甲后,再走1440米才到达
C.甲乙两人之间的最远距离是300米
D.甲到终点时,乙已经在终点处休息了6分钟
4.人工智能的发展使得智能机器人送餐成为时尚.如图,某餐厅的机器人小数和小文从厨房门口出发,准备给相距450cm的客人送餐,小数比小文先出发,且速度保持不变,小文出发一段时间后将速度提高到原来的2倍.设小数行走的时间为x(s),小数和小文行走的路程分别为y1(cm),y2(cm),y1,y2与x之间的函数图象如图所示,则下列说法不正确的是( )
A.小数比小文先出发15秒
B.小文提速后的速度为30cm/s
C.n=40
D.从小数出发至送餐结束,小文和小数最远相距150cm
5.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时,甲离终点还有320米,其中正确的结论有( )
A.①② B.①③ C.①④ D.③④
6.已知甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的距离s(km)与甲货车出发时间t(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.则下列说法错误的是( )
A.乙货车的速度为60km/h
B.乙到终点时,t=4
C.点E的坐标为(4,180)
D.两车之间距离为100km时,t=1.4h或3.4h
二.填空题
7.某快递公司每天上午9:30﹣10:30为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么从9:30开始,经过 分钟时,两仓库快递件数相同.
8.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进.如图所示,l1和l2分别表示两人到小亮家的距离s(km)和时间t(h)的关系,则出发 h后两人相遇.
9.德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加,甲、乙两名选手同时参加了往返10km(单程5km)的业余组比赛,如果全程保持匀速,甲,乙之间的距离s(km)与甲所用的时间t(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 km.
10.快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离s(km)与行驶时间t(h)之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 km/h.
三.解答题
11.大运河畔有一条笔直的健身步道,小明、小亮分别从相距1500米的M、N两点同时出发,相向而行.两人离M点的距离s关于时间t的函数关系如图中折线所示.小明跑了一段路之后与小亮相距250米,休息1分钟之后与小亮相距400米,小明继续跑了4分钟后与小亮同时到达各自终点.
(1)a的值为 ;
(2)求图中BC所对应的函数表达式;
(3)求小明、小亮相遇的时间.
12.一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早小时到达目的地.甲、乙两车之间的路程y km与两车行驶时间x h的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
13.领航无人机表演团队进行无人机表演训练,甲无人机以a米/秒的速度从地面起飞,乙无人机从距离地面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙无人机按照训练计划准时到达距离地面的高度为96米时,进行了时长为t秒的联合表演,表演完成后以相同的速度大小同时返回地面.甲、乙两架无人机所在的位置距离地面的高度y(米)与无人机飞行的时间x(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)a= 米/秒,t= 秒;
(2)求线段MN所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米?(直接写出答案即可)
14.一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地,小时后,一辆货车从A地出发,沿同一路线每小时行驶80千米匀速驶向B地,货车到达B地填装货物耗时15分钟,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是 千米,a= ;
(2)求线段FG所在直线的函数解析式;
(3)货车出发多少小时两车相距15千米?(直接写出答案即可)
15.1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.两个气球都上升了1h.1号、2号气球所在位置的海拔y1,y2(单位:m)与上升时间x(单位:min)的函数关系如图所示.请根据图象回答下列问题:
(1)a= ,b= ;
(2)请分别求出y1,y2与x的函数关系式;
(3)当上升多长时间时,两个气球的海拔竖直高度差为5m?
16.在一条高速公路上依次有A,B,C三地,甲车从A地出发匀速驶向C地,到达C地休息1h后调头(调头时间忽略不计)按原路原速驶向B地,甲车从A地出发1.5h后,乙车从C地出发匀速驶向A地,两车同时到达目的地.两车距A地路程y km与甲车行驶时间x h之间的函数关系如图所示.请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,乙车行驶的速度是 km/h;
(2)求图中线段MN所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时,两车距各自出发地路程的差是160km?请直接写出答案.
17.已知甲,乙两地相距480km,一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车继续出发h后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是 ;
(2)求货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数关系式;
(3)直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距12km.
18.已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
(1)m= ,n= ;
(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的路程.
19.在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米?(直接写出答案即可)
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 A D C C B C
1.【解答】解:由图象可得:A,B两地相距为360+60=420(km),故①正确;
货车的速度为:60÷2=30(km/h),
故货车到达A地一共需要2+360÷30=14(h),
设两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=kx+b,
由题意可得:,
解得:,
∴y2=30x﹣60,故②正确;
设客车离C站的路程y1与行驶时间x之间的函数关系式为y=mx+n,
由题意可得:,
解得,
∴y1=﹣60x+360,故③正确;
由y1=y2得﹣60x+360=30x﹣60,
解得:,
∵,
∴符合题意,即客、货两车在小时相遇,故④正确;
故选:A.
2.【解答】解:图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③正确;
当乙追上甲后,令y乙﹣y甲=50,100t﹣100﹣60t=50
解得,
当乙到达目的地,甲自己行走时,y甲=60t=250,
解得,
∴综上所述,当乙追上甲后,甲乙两车相距50千米时,或.故④正确;
综上可知正确的有①②③④,共4个.
故选:D.
3.【解答】解:16﹣4=12(分),
∴乙用12分钟追上甲,
∴A正确,不符合题意;
甲的速度为240÷4=60(米/分),
乙追上甲时,二人离起点的距离为2400﹣60×16=1440(米),
∴乙追上甲后,再走1440米才到达,
∴B正确,不符合题意;
乙的速度为60×16÷(16﹣4)=80(米/分),
乙到达终点所用的时间为2400÷80=30(分),
当乙到达终点时甲走的路程为60×(30+4)=2040(米),
当乙到达终点时,甲、乙二人的距离最远,为2400﹣2040=360(米),
∴C错误,符合题意;
∵当乙到达终点时甲走的路程为2040米,
∴甲还需要(2400﹣2040)÷60=6(分)到达终点,
∴甲到终点时,乙已经在终点处休息了6分钟,
∴D正确,不符合题意.
故选:C.
4.【解答】解:根据图象,小数比小文先出发15秒,
∴A正确,不符合题意;
小文提速前的速度为30÷(17﹣15)=15(cm/s),
∴小文提速后的速度为15×2=30(cm/s),
∴B正确,不符合题意;
∵30(m﹣17)=450﹣30,
∴m=31,
∴小数的速度为310÷31=10(cm/s),
∴小数到达目的地所用时间为450÷10=45(s),
∴n=45,
∴C不正确,符合题意;
小数和小文相遇前,当x=15时小文和小数相距最远,为10×15=150(cm),
小数和小文相遇后,当x=m=31时小文和小数相距最远,为450﹣10×31=140(cm),
∵150>140,
∴从小数出发至送餐结束,小文和小数最远相距150cm,
∴D正确,不符合题意.
故选:C.
5.【解答】解:甲步行的速度为240÷4=60(米/分),
∴①正确,符合题意;
乙用16﹣4=12(分)追上甲,
∴②不正确,不符合题意;
设乙的速度为v米/分,则12(v﹣60)=240,
解得v=80,
则乙走完全程用了2400÷80=30(分),
∴③正确,符合题意;
乙到达终点时,甲离终点还有2400﹣60×(30+4)=360(米),
∴④不正确,不符合题意.
综上,①③正确.
故选:B.
6.【解答】解:设乙货车的速度为v km/h,则2.4(40+v)=240,
解得v=60,
∴乙货车的速度为60km/h,
∴A正确,不符合题意;
乙到终点时所用时间为240÷60=4(h),
∴B正确,不符合题意;
根据②,当乙到达终点时,甲距离A地40×4=160(km),
∴当乙到终点时,甲乙相距160km,
点E的坐标为(4,160),
∴C不正确,符合题意;
设线段CD对应的函数关系式为s=k1t+b1(k1、b1为常数,且k1≠0),
将坐标C(0,240)和D(2.4,0)分别代入s=k1t+b1,
得,
解得,
∴线段CD对应的函数关系式为s=﹣100t+240(0≤t≤2.4),
当s=100时,得﹣100t+240=100,
解得t=1.4;
设线段DE对应的函数关系式为s=k2t+b2(k2、b2为常数,且k2≠0),
将坐标D(2.4,0)和E(4,160)分别代入s=k2t+b2,
得,
解得,
∴线段DE对应的函数关系式为s=100t﹣240,
当s=100时,得100t﹣240=100,
解得t=3.4,
∴当t=1.4h或3.4h时,两车之间距离为100km,
∴D正确,不符合题意.
故选:C.
二、填空题
7.【解答】解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=﹣4,
∴y2=﹣4x+240,
联立,
解得,
∴经过20分钟时,当两仓库快递件数相同.
故答案为:20
8.【解答】解:设l1的函数解析式为y1=kx+b,
则,
解得,
∴l1的函数解析式为S1=5t+3.5;
设l2的函数解析式为S2=mt,
则0.4m=6,
解得m=15,
∴l2的函数解析式为S2=15t;
令S1=S2,即5t+3.5=15t,
解得t=0.35,
∴出发0.35小时后两人相遇.
故答案为:0.35.
9.【解答】解:设甲的速度为x千米/小时,则乙的速度为(x﹣4)千米/小时,
则:[(x﹣4)+x]=10,
解得:x=10,
乙的速度为 10﹣4=6km/h,甲到终点的时间为:10÷10=1h,
此时,乙走过的路程为:1×6=6km,
所以,乙距离终点:10﹣6=4km.
10.【解答】解:∵快递员始终匀速行驶,
∴快递员的行驶速度是35(km/h).
故答案为:35.
三、解答题
11.【解答】解:(1)由题意可知,小亮的速度是400﹣250=150(m/min),
1500÷150=10(min),
∴a=10.
故答案为:10.
(2)10﹣4=6(min),
6min时小亮与N点的距离为150×6=900(m),则此时小明与M点的距离为1500﹣900+400=1000(m),
∴B(6,1000).
设BC所对应的函数表达式为s=kt+b(k、b为常数,且k≠0),
将B(6,1000)和C(10,1500)分别代入s=kt+b,
得,
解得,
∴BC所对应的函数表达式为s=125t+250(6≤t≤10).
(3)∵B(6,1000),
∴A(5,1000),
∴小明的速度为1000÷5=200(m/min),
1500÷(200+150)(min).
答:小明、小亮相遇的时间为min.
12.【解答】解:(1)由图可知,甲车小时行驶的路程为(200﹣180)km,
∴甲车行驶的速度是,
70×(4)=300(km),
填图如下:
故答案为:70;
(2)由图可知E,F的坐标分别为,(4,180),
设线段EF所在直线的函数解析式为y=kx+b,
则,
解得,
∴线段EF所在直线的函数解析式为y=120x﹣300;
(3)由题意知,A、C两地的距离为:,
乙车行驶的速度为:,
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300﹣200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况:
甲在AB之间时:
200﹣50x=3(100﹣70x),
解得;
甲在BC之间时:
200﹣50x=3(70x﹣100),
解得;
综上可知,两车出发或时,乙车距B地的路程是甲车距B地路程的3倍.
13.【解答】解:(1)由题意得甲无人机的速度为 a=48÷6=8(米/秒),
t=39﹣19=20(秒).
故答案为:8,20;
(2)由图象知,N(19,96),
∵甲无人机的速度为8米/秒,
∴甲无人机匀速从0米到96米所用时间为96÷8=12(秒),
∴甲无人机单独表演所用时间为19﹣12=7(秒),
6+7=13(秒),
∴M(13,48),
设线段MN所在直线的函数解析式为y=kx+b,
将M(13,48),N(19,96)代入得
,
解得
∴线段MN所在直线的函数解析式为y=8x﹣56.
(3)由题意A(0,20),B(6,48),
同理线段OB所在直线的函数解析式为y=8x,
线段AN所在直线的函数解析式为y=4x+20,
线段BM所在直线的函数解析式为y=48,
当0≤x≤6时,由题意得|4x+20﹣8x|=12,
解得x=2或x=8(舍去),
当6<x≤13时,由题意得|4x+20﹣48|=12,
解得x=10或x=4(舍去),
当13<x≤19时,由题意得|8x﹣56﹣4x﹣20|=12,
解得x=16或x=22(舍去),
综上,两架无人机表演训练到2秒或10秒或16秒时,它们距离地面的高度差为12米.
14.【解答】解:(1)∵8060(千米),
∴A,B两地之间的距离是60千米;
∵货车到达B地填装货物耗时15分钟,
∴a1,
故答案为:60,1;
(2)设线段FG所在直线的解析式为y=kx+b(k≠0),将F(1,60),G(2,0)代入得:
,
解得 ,
∴线段FG所在直线的函数解析式为y=﹣60x+120;
(3)巡逻车速度为60÷(2)=25(千米/小时),
∴线段CD的解析式为y=25x+2525x+10(0≤x≤2),
当货车第一次追上巡逻车后,80x﹣(25x+10)=15,
解得x;
当货车返回与巡逻车未相遇时,(﹣60x+120)﹣(25x+10)=15,
解得x;
当货车返回与巡逻车相遇后,(25x+10)﹣(﹣60x+120)=15,
解得x;
综上所述,货车出发小时或 小时或小时,两车相距15千米.
15.【解答】解:(1)∵1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.
当x=20时,两球相遇,
y1=10+x=10+20=30,
∴b=30,
设2号探测气球解析式为y2=20+ax,
∵y2=20+ax过(20,30),
∴30=20+20a,
解得a=0.5,
∴y2=20+0.5x,
故答案为:0.5,30;
(2)根据题意得:
1号探测气球所在位置的海拔:y1=10+x,
2号探测气球所在位置的海拔:y2=20+0.5x;
(3)分两种情况:
①2号探测气球比1号探测气球海拔高5米,根据题意得:
(20+0.5x)﹣(x+10)=5,
解得x=10;
②1号探测气球比2号探测气球海拔高5米,根据题意得:
(x+10)﹣(0.5x+20)=5,
解得x=30.
综上所述,上升了10或30min后这两个气球相距5m.
16.【解答】解:(1)由图可得D(3,360),即甲出发3时后与A地相距360km,
∴甲车行驶速度为120(km/h),
由题意可得,乙车出发1.5h行驶120km,
∴乙车行驶速度为 80(km/h),
故答案为:120,80;
(2)设线段MN所在直线的解析式为 y=kx+b(k≠0),
将(1.5,360),(3,240)代入y=kx+b,
得,
解得,
∴线段MN所在直线的解析式为y=﹣80x+480(1.5≤x≤6);
(3)由题意可得,当y=0时,x=6,
∴N(6,0),
∵两车同时到达目的地,
∴乙到达目的地时,甲距离A地的距离为360﹣120×(6﹣3﹣1)=120(km),
∴F(6,120),E(4,360),
设乙车出发t时,两车距各自出发地路程的差是160km,
当0<t≤1.5时,此时甲在到达C地前,则|80t﹣120×(t+1.5)|=160,
解得t为负数,不合题意;
当1.5<t≤2.5时,此时甲在C地休息,则|80t﹣360|=160,
解得t1=2.5,t2=6.5(不合题意,舍去);
当2.5<t≤4.5时,此时甲掉头驶向B地,则|80t﹣[2×360﹣120×(t+1.5﹣1)]|=160,
解得t1=2.5(不合题意,舍去),t2=4.1;
综上,乙车出发2.5h或4.1h,两车距各自出发地路程的差是160km.
17.【解答】解:(1)由图象知,C(4,480),
设直线OC的解析式为y=kx,把C(4,480)代入得,480=4k,
解得k=120,
∴直线OC的解析式为y=120x;把(1,a)代入y=120x,得a=120,
故答案为:120;
(2)由停下来装完货物后,发现此时与出租车相距120km,货车行驶时间为小时,
∵a=120(km),
∴货车卸货时与乙地相距120km,
∴出租车距离乙地为120+120=240(km),
∴出租车距离甲地为480﹣240=240(km),
把y=240代入y=120x得,240=120x,
解得x=2,
∴货车装完货物时,x=2,B(2,120),
根据货车继续出发h后与出租车相遇,
可得(出租车的速度+货车的速度)=120,
根据直线OC的解析式为y=120x(0≤x≤4),
可得出租车的速度为120km/h,
∴相遇时,货车的速度为120120=60(km/h),
故可设直线BG的解析式为y=60x+b,
将B(2,120)代入y=60x+b,可得120=120+b,
解得b=0,
∴直线BG的解析式为y=60x(2≤x≤8),
故货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数关系式为y=60x,
(3)把y=480代入y=60x,可得480=60x,
解得x=8,
∴G(8,480),
∴F(8,0),
根据出租车到达乙地后立即按原路返回,经过比货车早15分钟到达甲地,可得EF,
∴,
∴出租车返回后的速度为480÷()=128km/h,
设在出租车返回的行驶过程中,货车出发t小时,与出租车相距12km,
此时货车距离乙地为60t km,出租车距离乙地为128(t﹣4)=(128t﹣512)km,
①出租车和货车第二次相遇前,相距12km时,可得60t1﹣(128t1﹣512)=12,
解得t1;
②出租车和货车第二次相遇后,相距12km时,可得(128t2﹣512)﹣60t2=12,
解得t2,
故在出租车返回的行驶过程中,货车出发h或h与出租车相距12km.
18.【解答】解:(1)由题意知:m=200÷100=2,
n=m+4=2+4=6,
故答案为:2,6;
(2)设y=kx+b,将(2,200),(6,440)代入得:
,
解得,
∴y=60x+80,(2≤x≤6);
(3)乙车的速度为(440﹣200)÷2=120(千米/小时),
∴乙车到达A地所需时间为440÷120(小时),
当x时,y=6080=300,
∴甲车距A地的路程为300千米.
19.【解答】解:(1)由图象知:当x=0时,y=1200,
∴A、B两地之间的距离是1200米;
由图象知:乙经过20分钟到达A,
∴乙的速度为60(米/分).
故答案为:1200;60;
(2)由图象知:当x时,y=0,
∴甲乙二人的速度和为:1200140(米/分),
设甲的速度为x米/分,则乙的速度为(140﹣x)米/分,
∴140﹣x==60,
∴x=80.
∴甲的速度为80(米/分),
∵点M的实际意义是经过c分钟甲到达B地,
∴c=1200÷80=15(分钟),
∴a=60×15=900(米).
∵点N的实际意义是经过20分钟乙到达A地,
∴b=900﹣(80﹣60)×5=800(米);
故答案为:900;800;15;
(3)由题意得:M(15,900),N(20,800),
设线段MN的解析式为y=kx+n,
∴,
解得:,
∴线段MN的解析式为y=﹣20x+1200(15≤x≤20);
(4)在乙运动的过程中,二人出发后第8分钟和第分钟两人相距80米.理由:
①相遇前两人相距80米时,二人的所走路程和为1200﹣80=1120(米),
∴1120÷140=8(分钟);
②相遇后两人相距80米时,二人的所走路程和为1200+80=1280(米),
∴1280÷140(分钟).
综上,在乙运动的过程中,二人出发后第8分钟和第分钟两人相距80米.
21世纪教育网(www.21cnjy.com)
同课章节目录
