2025年数学中考专题一轮复习课件:3.11 函数 (共36张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:3.11 函数 (共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 17:14:07 | ||
图片预览











文档简介
(共36张PPT)
2025年数学中考复习
基础知识
项目三 函数
考点要求
壹
能在实际问题中列出一次函数的表达式,并结合一次函数的图像与表达式的性质等解决简单的实际问题.
核心知识点
贰
常见问题类型 常用关系式
购买、销售、分配问题 费用=单价×数量;
利润=售价一进价;
总销售额=销售单价×总销售量;
利润率= ×100%.
常见问题类型 常用关系式
生产、工程问题 工作效率=
生产总量=生产效率×生产时间
路程问题 路程=速度×时间.
考点攻坚
叁
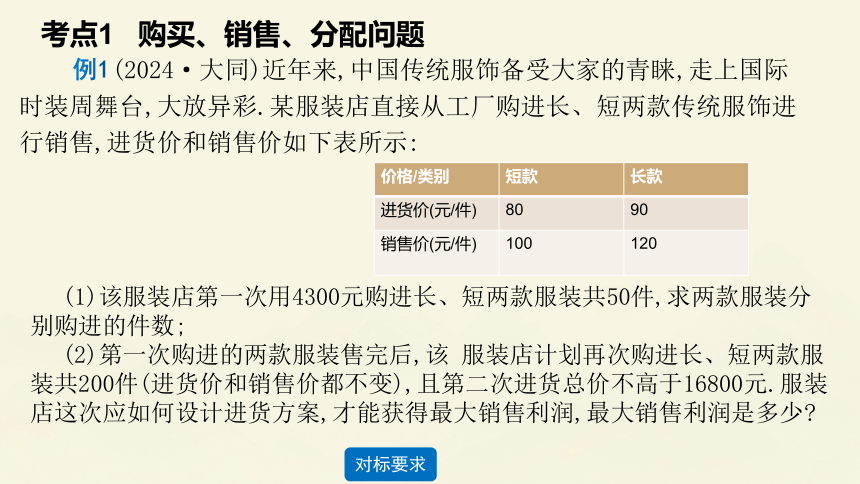
(2024·大同)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如下表所示:
考点1 购买、销售、分配问题
例1
(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数;
(2)第一次购进的两款服装售完后,该 服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
价格/类别 短款 长款
进货价(元/件) 80 90
销售价(元/件) 100 120
【解析】
(1)设购进短款服装件,购进长款服装件,由题意,得
答:长款服装购进30件,短款服装购进20件.
(2)设第二次购进件短款服装,则购进件长款服装,由题意,得
∴.
解得
又设利润为元,
则.
∵,
∴随的增大而减小.
∴当时,利润最大为:(元).
答:当购进120件短款服装和80件长款服装时有最大利润,最大利润是4800元.
(2024·东莞)
例2
考点2 生产、工程问题
背景
【缤纷618,优惠送大家】今年618各大电商平台促销火热, 线下购物中心也亮出大招,年中大促进 入“白热化”.深圳各大购物中心早在5月 就开始推出618活动,进入6月更是持续 加码,如图所示,某商场为迎接即将到来 的618优惠节,采购了若干辆购物车.
素材
右图为某商场叠放的购物车,图为购物车叠放在一起的示意图,若一辆购物车车身长1m,每增加一辆购物车,车身增加0.2m.
问题解决
任务 1
若某商场采购了辆购物车,求车身总长与购物车辆数的表达式;
任务 2
若该商场用直立电梯从一楼运输该批购物车到二楼,已知该商场的直立电梯长为2.6m,且一次可以运输两列购物车,求直立电梯一次性最多可以运输多少辆购物车
任务 3
若该商场扶手电梯一次性可以运输24辆购物车,若要运输100辆购物车,且共使用电梯5次,求:共有多少种运输方案
【解析】解:任务1.
根据题意得:,
∴车身总长与购物车辆数的表达式为,为正整数;
任务2.
当时,, 解得, (辆),
答:直立电梯一次性最多可以运输18辆购物车;
任务3.
设用扶手电梯运输次,直立电梯运输次,
∵100÷244 ,
∴根据题意得: 解得≥53,
∵为正整数,且, ∴2,3,4,5, ∴共有4种运输方案.
专项训练
肆
达标训练
1.(2024·青岛)同一条公路连接三地,地在两地之间.甲、乙两车分别从地、地同时出发前往地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离(km)与时间(h)的函数关系.下列结论正确的是( A)
A.甲车行驶 h与乙车相遇
B.A,C两地相距220 km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
2.(2023·洛阳)甲乙两地相距千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离(千米)与两人行驶时刻(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为(A)
A.8:28 B.8:30 C.8:32 D.8:35
3.(2022·长沙)桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐甲、乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程(km)随时间(h)变化的图像如图所示.依据图中信息,下列说法中错误的是( C)
A.甲大巴比乙大巴先到达景点
B.甲大巴中途停留了0.5h
C.甲大巴停留后用1.5h追上乙大巴
D.甲大巴停留前的平均速度是60km/h
4.(2023·广西)【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心。”某兴趣小组将利用物理学中杠杆原理制作简易杆秤,小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务。
【知识背景】如下页图所示,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得,其中秤盘质量克,重物质量克,秤砣质量克,秤纽与秤盘的水平距离为1厘米,秤组与零刻线的水平距离为厘米,秤砣与零刻线的水平距离为厘米.
【方案设计】目标:设计简易杆秤.设定,最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
任务一:确定和的值.
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于的方程;
(2)当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于的方程;
(3)根据(1)和(2)所列方程,求出和的值;
任务二:确定刻线的位置.
(4)根据任务一,求关于的函数解析式;
(5)从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离.
4.解:(1)由题意得:
(2)由题意得:
(3)由(1)(2)可得:
(4)由(3)可知:
答案
(5)由(4)可知:
∴当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;
∴相邻刻线间的距离为5厘米.
答案
课堂练习
伍
1.(2023·南京)某品牌鞋子的长度cm与鞋子的码数之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )
B
A.23cm B.24cm C.25cm D.26cm
2.(2022·嘉兴)下表中记录了一次试验中时间和温度的数据.
若温度的变化是均匀的,则14分钟时的温度是 ℃.
52
时间/分钟 0 5 10 15 20 25
温度/℃ 10 25 40 55 70 85
3.(2022·齐齐哈尔)某超市糯米的价格为5元/千克,端午节推出促销活动:一次购买的数量不超过2千克时,按原价售出,超过2千克时,超过的部分打8折.若某人付款14元,则他购买了 3千克糯米;设某人的付款金额为元,购买量为千克,则购买量关于付款金额()的函数解析式为 .
4.(2023· 丽水)2022年8月27日至29日,以“新能源、新智造、新时代”为主题的世界清洁能源装备大会在德阳举行.大会聚焦清洁能源装备产业发展热点和前 瞻性问题,着力实现会展聚集带动产业聚 集,其中德阳清洁能源装备特色小镇位于德 阳经济技术开发区,规划面积4.82平方公里,计划2025年基本建成.若甲、乙两个工程队计划参与修建“特色小镇”中的某项工程,已知由甲单独施工需要18个月完成任务,若由乙先单独施工2个月,再由甲、乙合作施工10个月恰好完成任务.承建公司每个月需要向甲工程队支付施工费用8万元,向乙工程队支付施工费用5万元.
(1)乙队单独施工需要几个月才能完成任务
(2)为保证该工程在两年内完工,且尽可能的减少成本,承建公司决定让甲、乙两个工程队同时施工,并将该工程分成两部分,甲队完成其中一部分工程用了个月,乙队完成另一部分工程用了个月,已知甲队施工时间不超过6个月,乙队施工时间不超过24个月,且,为正整数,则甲、乙两队实际施工的时间安排有几种方式 哪种安排方式所支付费用最低
答案
4.解。(1)设乙队单独施工需要个月才能完成任务,根据题意得,
解得=27。经检验=27是原方程的根。
答:乙队单独施工需要27个月才能完成任务;
2 +(+=1
(2)根据题意得
整理得,
∵a,b是正整数,a≤6,b≤24,
∴b为3的倍数,
∴b=24时,a=2;b=21时,a=4;b=18时,a=6,
=18-
∴方案一:甲队施工2个月,乙队施工24个月;方案二:甲队施工4个月,乙队施工21个月;方案三:甲队施工6个月,乙队施工18个月;
设:甲乙两队实际施工的费用为w万元,
得,w=8a+5b=8×(18-)+5b=-+144
∵k=-<0
∴w 随b的增大而减小,即当b最大=24时,所支付费用w最低。∴方案一:甲队施工2个月,乙队施工24个月,所支付费用最低。
5.(2022·陕西)龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(表示兔子和乌龟从起点出发所走的时间,,分别表示兔子与乌龟所走的路程).下列说法错误的是(C)
A.兔子和乌龟的比赛路程是500米
B.中途,兔子比乌龟多休息了35分钟
C.兔子比乌龟多走了50米
D.比赛结果,兔子比乌龟早5分钟到达终点
6.(2023·武汉)我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之 ”下图是善行者与不善行者行走路程(单位:步) 关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 .
250
7.(2023·大理)某食用油的沸点温度远高于水的沸点温度.小聪想用刻度不超过100℃的温度计测算出这种食用油沸点的温度.在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔10s测量一次锅中油温,得到的数据记录如下.
时间t/s 0 10 20 30 40
温度y/℃ 10 30 40 50 70
(1)小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温(单位:℃)与加热的时间(单位:s)符合初中学习过的某种函数关系,填空:
可能是 函数关系(选填“正比例”“一次”“二次”“反比例”);
(2)根据以上判断,求关于的函数解析式;
(3)当加热110s时,油沸腾了,请推算沸点的温度.
一次
答案
7.(1)根据表格中两个变量对应值变化的规律可知,时间每增加10s,油的温度就升高20℃,故锅中油温与加热的时间可能是一次函数关系;故答案为:一次;
(2)设锅中油温与加热的时间的函数关系式为(),.将点(,10),(10,30)代入得,解得:
∴;
(3)当时,,∴经过推算,该油的沸点温度是230℃.
谢谢观看
2025年数学中考复习
基础知识
项目三 函数
考点要求
壹
能在实际问题中列出一次函数的表达式,并结合一次函数的图像与表达式的性质等解决简单的实际问题.
核心知识点
贰
常见问题类型 常用关系式
购买、销售、分配问题 费用=单价×数量;
利润=售价一进价;
总销售额=销售单价×总销售量;
利润率= ×100%.
常见问题类型 常用关系式
生产、工程问题 工作效率=
生产总量=生产效率×生产时间
路程问题 路程=速度×时间.
考点攻坚
叁
(2024·大同)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如下表所示:
考点1 购买、销售、分配问题
例1
(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数;
(2)第一次购进的两款服装售完后,该 服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
价格/类别 短款 长款
进货价(元/件) 80 90
销售价(元/件) 100 120
【解析】
(1)设购进短款服装件,购进长款服装件,由题意,得
答:长款服装购进30件,短款服装购进20件.
(2)设第二次购进件短款服装,则购进件长款服装,由题意,得
∴.
解得
又设利润为元,
则.
∵,
∴随的增大而减小.
∴当时,利润最大为:(元).
答:当购进120件短款服装和80件长款服装时有最大利润,最大利润是4800元.
(2024·东莞)
例2
考点2 生产、工程问题
背景
【缤纷618,优惠送大家】今年618各大电商平台促销火热, 线下购物中心也亮出大招,年中大促进 入“白热化”.深圳各大购物中心早在5月 就开始推出618活动,进入6月更是持续 加码,如图所示,某商场为迎接即将到来 的618优惠节,采购了若干辆购物车.
素材
右图为某商场叠放的购物车,图为购物车叠放在一起的示意图,若一辆购物车车身长1m,每增加一辆购物车,车身增加0.2m.
问题解决
任务 1
若某商场采购了辆购物车,求车身总长与购物车辆数的表达式;
任务 2
若该商场用直立电梯从一楼运输该批购物车到二楼,已知该商场的直立电梯长为2.6m,且一次可以运输两列购物车,求直立电梯一次性最多可以运输多少辆购物车
任务 3
若该商场扶手电梯一次性可以运输24辆购物车,若要运输100辆购物车,且共使用电梯5次,求:共有多少种运输方案
【解析】解:任务1.
根据题意得:,
∴车身总长与购物车辆数的表达式为,为正整数;
任务2.
当时,, 解得, (辆),
答:直立电梯一次性最多可以运输18辆购物车;
任务3.
设用扶手电梯运输次,直立电梯运输次,
∵100÷244 ,
∴根据题意得: 解得≥53,
∵为正整数,且, ∴2,3,4,5, ∴共有4种运输方案.
专项训练
肆
达标训练
1.(2024·青岛)同一条公路连接三地,地在两地之间.甲、乙两车分别从地、地同时出发前往地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离(km)与时间(h)的函数关系.下列结论正确的是( A)
A.甲车行驶 h与乙车相遇
B.A,C两地相距220 km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
2.(2023·洛阳)甲乙两地相距千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离(千米)与两人行驶时刻(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为(A)
A.8:28 B.8:30 C.8:32 D.8:35
3.(2022·长沙)桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐甲、乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程(km)随时间(h)变化的图像如图所示.依据图中信息,下列说法中错误的是( C)
A.甲大巴比乙大巴先到达景点
B.甲大巴中途停留了0.5h
C.甲大巴停留后用1.5h追上乙大巴
D.甲大巴停留前的平均速度是60km/h
4.(2023·广西)【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心。”某兴趣小组将利用物理学中杠杆原理制作简易杆秤,小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务。
【知识背景】如下页图所示,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得,其中秤盘质量克,重物质量克,秤砣质量克,秤纽与秤盘的水平距离为1厘米,秤组与零刻线的水平距离为厘米,秤砣与零刻线的水平距离为厘米.
【方案设计】目标:设计简易杆秤.设定,最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
任务一:确定和的值.
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于的方程;
(2)当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于的方程;
(3)根据(1)和(2)所列方程,求出和的值;
任务二:确定刻线的位置.
(4)根据任务一,求关于的函数解析式;
(5)从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离.
4.解:(1)由题意得:
(2)由题意得:
(3)由(1)(2)可得:
(4)由(3)可知:
答案
(5)由(4)可知:
∴当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;当时,则有;
∴相邻刻线间的距离为5厘米.
答案
课堂练习
伍
1.(2023·南京)某品牌鞋子的长度cm与鞋子的码数之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )
B
A.23cm B.24cm C.25cm D.26cm
2.(2022·嘉兴)下表中记录了一次试验中时间和温度的数据.
若温度的变化是均匀的,则14分钟时的温度是 ℃.
52
时间/分钟 0 5 10 15 20 25
温度/℃ 10 25 40 55 70 85
3.(2022·齐齐哈尔)某超市糯米的价格为5元/千克,端午节推出促销活动:一次购买的数量不超过2千克时,按原价售出,超过2千克时,超过的部分打8折.若某人付款14元,则他购买了 3千克糯米;设某人的付款金额为元,购买量为千克,则购买量关于付款金额()的函数解析式为 .
4.(2023· 丽水)2022年8月27日至29日,以“新能源、新智造、新时代”为主题的世界清洁能源装备大会在德阳举行.大会聚焦清洁能源装备产业发展热点和前 瞻性问题,着力实现会展聚集带动产业聚 集,其中德阳清洁能源装备特色小镇位于德 阳经济技术开发区,规划面积4.82平方公里,计划2025年基本建成.若甲、乙两个工程队计划参与修建“特色小镇”中的某项工程,已知由甲单独施工需要18个月完成任务,若由乙先单独施工2个月,再由甲、乙合作施工10个月恰好完成任务.承建公司每个月需要向甲工程队支付施工费用8万元,向乙工程队支付施工费用5万元.
(1)乙队单独施工需要几个月才能完成任务
(2)为保证该工程在两年内完工,且尽可能的减少成本,承建公司决定让甲、乙两个工程队同时施工,并将该工程分成两部分,甲队完成其中一部分工程用了个月,乙队完成另一部分工程用了个月,已知甲队施工时间不超过6个月,乙队施工时间不超过24个月,且,为正整数,则甲、乙两队实际施工的时间安排有几种方式 哪种安排方式所支付费用最低
答案
4.解。(1)设乙队单独施工需要个月才能完成任务,根据题意得,
解得=27。经检验=27是原方程的根。
答:乙队单独施工需要27个月才能完成任务;
2 +(+=1
(2)根据题意得
整理得,
∵a,b是正整数,a≤6,b≤24,
∴b为3的倍数,
∴b=24时,a=2;b=21时,a=4;b=18时,a=6,
=18-
∴方案一:甲队施工2个月,乙队施工24个月;方案二:甲队施工4个月,乙队施工21个月;方案三:甲队施工6个月,乙队施工18个月;
设:甲乙两队实际施工的费用为w万元,
得,w=8a+5b=8×(18-)+5b=-+144
∵k=-<0
∴w 随b的增大而减小,即当b最大=24时,所支付费用w最低。∴方案一:甲队施工2个月,乙队施工24个月,所支付费用最低。
5.(2022·陕西)龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(表示兔子和乌龟从起点出发所走的时间,,分别表示兔子与乌龟所走的路程).下列说法错误的是(C)
A.兔子和乌龟的比赛路程是500米
B.中途,兔子比乌龟多休息了35分钟
C.兔子比乌龟多走了50米
D.比赛结果,兔子比乌龟早5分钟到达终点
6.(2023·武汉)我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之 ”下图是善行者与不善行者行走路程(单位:步) 关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 .
250
7.(2023·大理)某食用油的沸点温度远高于水的沸点温度.小聪想用刻度不超过100℃的温度计测算出这种食用油沸点的温度.在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔10s测量一次锅中油温,得到的数据记录如下.
时间t/s 0 10 20 30 40
温度y/℃ 10 30 40 50 70
(1)小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温(单位:℃)与加热的时间(单位:s)符合初中学习过的某种函数关系,填空:
可能是 函数关系(选填“正比例”“一次”“二次”“反比例”);
(2)根据以上判断,求关于的函数解析式;
(3)当加热110s时,油沸腾了,请推算沸点的温度.
一次
答案
7.(1)根据表格中两个变量对应值变化的规律可知,时间每增加10s,油的温度就升高20℃,故锅中油温与加热的时间可能是一次函数关系;故答案为:一次;
(2)设锅中油温与加热的时间的函数关系式为(),.将点(,10),(10,30)代入得,解得:
∴;
(3)当时,,∴经过推算,该油的沸点温度是230℃.
谢谢观看
同课章节目录
