2025年数学中考专题一轮复习课件 3.12 反比例函数的图象与性质及其应用(共37张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件 3.12 反比例函数的图象与性质及其应用(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 20:33:08 | ||
图片预览










文档简介
(共37张PPT)
2025年数学中考复习
3.12 反比例函数的图象
与性质及其应用
基础知识
项目三 函数
考点要求
壹
1.结合具体情境,体会反比例函数的意义,能根据已知条件确定反比例函数的表达式;
2.能画出反比例函数的图像,根据图象和表达式探索并理解和时图象的变化情况;
3.能用反比例函数解决简单实际问题.
核心知识点
贰
知识点1 反比例函数的定义
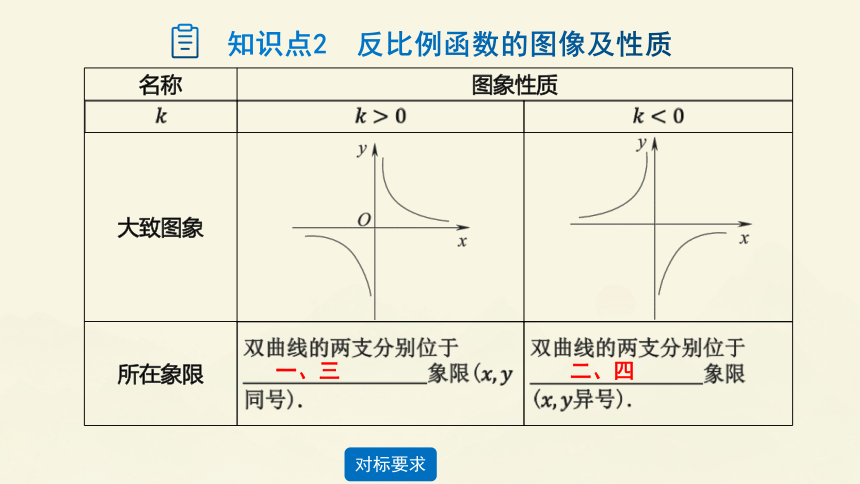
知识点2 反比例函数的图像及性质
名称 图象性质
大致图象
所在象限 双曲线的两支分别位于 象限(同号). 双曲线的两支分别位于
象限(异号).
一、三
二、四
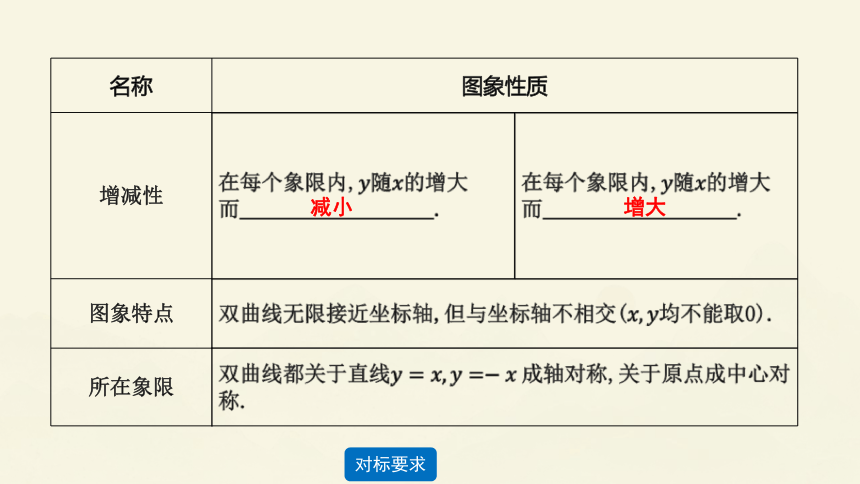
名称 图象性质 增减性 在每个象限内,的增大而 . 在每个象限内,的增大而 .
图象特点 双曲线无限接近坐标轴,但与坐标轴不相交(均不能取0). 所在象限 双曲线都关于直线成轴对称,关于原点成中心对称. 减小
增大
知识点3 的几何意义
在反比例函数的图象上任取一点,并过点分别作坐标轴的垂线段,所围成的矩形面积.
注意:此时可以为负.
知识点4 求反比例函数解析式
待定系数法
需要一个点
利用的几何意义来求解
由矩形面积得,再通过观察函数图像中双曲线所在象限来判断的符号.
温馨提示:不管是实际问题还是通过函数图像得到的点的坐标,一定要注意的取值范围.
考点攻坚
叁
考点1 反比例函数图像的性质
例1
(2022·上海)已知反比例函数(),且在各自象限内随的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(2,3)
C.(3,0) D.(3,0)
【解析】因为反比例函数(),且在各自象限内随的增大而增大,所以A选项不符合题意;B选项符合题意;C选项不符合题意;D选项不符合题意.故选B.
(2024·广西)已知点,在反比例函数的图象上,若,则有( )
例2
【解析】本题考查了反比例函数的图象,熟练掌握反比例函数图象上点的坐标特征是解题的关键.根据点在反比例函数图象上,则满足关系式,横纵坐标的积等于2,结合即可得出答案.∵点
在反比例函数的图象上,∴,,∵,∴,,∴.故选A.
A.B. C.D
(2022·广西河池)如图所示,点,则该反比例函数的解析式为 .
例3
考点2 的几何意义
【解析】∵,∴.∵ 2,∴2.∴.∴,∴.∴该反比例函数的解析式为.
(2022·海南)若反比例函数的图象经过点(2,3),则它的图象也一定经过的点是( )
A.(2,3) B.(3,2)
C.(1,6) D.(6,1)
例4
考点3 求反比例函数解析式
【解析】,故C正确;,故D不正确.故选C.
专项训练
肆
1.(2023·太仓)函数与自变量的部分对应值如表所示,则下列函数表达式中,符合表中对应关系的可能是()
A.B.
C.D.
1 2 4
4 2 1
2.(2023·甘孜)已知点),在反比例函数的图象上,且,则下列结论一定正确的是( )
A.+B.+ C.- D.+
3.(2023·淄博)正在建设中的临滕高速是山东省“十四五”重点建设项目.一段工程施工需要运送的土石方总量为m ,设土石方日平均运送量为(单位:m /天),完成运送任务所需要的时间为(单位:天),则与满足()
A.反比例函数关系 B.正比例函数关系
C.一次函数关系 D.二次函数关系
4.如图所示,反比例函数()的图象与相交,某同学在内做随机扎针实验,针头落在阴影区域内的概率为 .
提升训练
5.(2023·广西)如图所示,过的图象上点,分别作轴,轴的平行线交的图象于,两点,以,为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为,,,,若,则的值为( )
A.4 B.3 C.2 D.1
6.(2024·徐州)如图所示,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点.
(1)求一次函数、反比例函数的表达式;
(2)连接求的面积.
答案
6.解:(1)∵一次函数y=k十b的图象与反比例函数y=的图象相交于点A(-1,n),B(2,1)
∴m=-n=2,
∴m=-2,n=-2,
∴反比例函数解析式为y=,
一次函数y=k十b的图象过A(-1,-2)、B(2,1)
2k+b=1
b=-1
∴一次函数解析式为y=-1
课堂练习
伍
1.(2024·成都)已知点(,)在反比例函数的图象上,则的值为( )
A. B. C. D.
2.(2023·四川)已知点,,均在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
3.近视眼镜的度数(度)与片焦距(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则之间的函数关系式是 .
4.(2024·江阴)杠杆平衡时,“阻力×阻力臂=动力×动力臂”.已知阻力和阻力臂分别为1600和0.5m,动力为(),动力臂为(m).则动力关于动力臂的函数表达式为 .
5.(2024·山西)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度(m/s)是载重后总质量(kg)的反比例函数.已知一款机器狗载重后总质量60kg时,它的最快移动速度6m/s;当其载重后总质量90kg时,它的最快移动速度 m/s
6.(2024·福州)如图,在平面直角坐标系中,反比例函数的图象与交于两点,且点都在第一象限.若(1,2),则点的坐标为 .
7.(2022·贵阳)如图所示,在平面直角坐标系中,等腰直角三角形的斜边轴于点,直角顶点在轴经过上,双曲线边的中点,若,则 .
8.(2024·长春)已知蓄电池电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的解析式(不要求写出自变量的取值范围).
(2)当电阻为3Ω时,求此时的电流.
答案
8.解:(1)设I=
由题意得:U=RI=9X4=36,
∴这个反比例函数的解析式为I=
(2)电阻R为3 时,I=12(A)。
9.(2024·东莞)一个人的脚印信息往往对应着这个人某些方面的基本特征. 某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高之间近似存在一个函数关系,部分数据如下表所示:
脚长(cm) … 23 24 25 26 27 28 …
身高y(cm) … 156 163 170 177 184 191 …
(1)在图1中描出表中数据对应的点;
(2)根据表中数据,从和中选择一个函数模型,它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出的取值范围);
(3)如图2,某场所发现了一个人的脚印,脚长约为25.8cm,请根据(2)中求出的函数解析式,估计这个人的身高.
答案
答案
(2)∵y=(k≠0)转化为k=y=23×156≠24×163≠25×170≠…
∴y与x的函数不可能是y=
故选一次函数y=a+b(a≠0),将点(23,156)、(24,163)代人解析式得:
解得
一次函数解析式为y=7—5。
(3)当x=25.8时,y=7×25.8—5=175.6(cmm)。
答:脚长约为25.8 cm,估计这个人的身高为175.6
-5
谢谢观看
2025年数学中考复习
3.12 反比例函数的图象
与性质及其应用
基础知识
项目三 函数
考点要求
壹
1.结合具体情境,体会反比例函数的意义,能根据已知条件确定反比例函数的表达式;
2.能画出反比例函数的图像,根据图象和表达式探索并理解和时图象的变化情况;
3.能用反比例函数解决简单实际问题.
核心知识点
贰
知识点1 反比例函数的定义
知识点2 反比例函数的图像及性质
名称 图象性质
大致图象
所在象限 双曲线的两支分别位于 象限(同号). 双曲线的两支分别位于
象限(异号).
一、三
二、四
名称 图象性质 增减性 在每个象限内,的增大而 . 在每个象限内,的增大而 .
图象特点 双曲线无限接近坐标轴,但与坐标轴不相交(均不能取0). 所在象限 双曲线都关于直线成轴对称,关于原点成中心对称. 减小
增大
知识点3 的几何意义
在反比例函数的图象上任取一点,并过点分别作坐标轴的垂线段,所围成的矩形面积.
注意:此时可以为负.
知识点4 求反比例函数解析式
待定系数法
需要一个点
利用的几何意义来求解
由矩形面积得,再通过观察函数图像中双曲线所在象限来判断的符号.
温馨提示:不管是实际问题还是通过函数图像得到的点的坐标,一定要注意的取值范围.
考点攻坚
叁
考点1 反比例函数图像的性质
例1
(2022·上海)已知反比例函数(),且在各自象限内随的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(2,3)
C.(3,0) D.(3,0)
【解析】因为反比例函数(),且在各自象限内随的增大而增大,所以A选项不符合题意;B选项符合题意;C选项不符合题意;D选项不符合题意.故选B.
(2024·广西)已知点,在反比例函数的图象上,若,则有( )
例2
【解析】本题考查了反比例函数的图象,熟练掌握反比例函数图象上点的坐标特征是解题的关键.根据点在反比例函数图象上,则满足关系式,横纵坐标的积等于2,结合即可得出答案.∵点
在反比例函数的图象上,∴,,∵,∴,,∴.故选A.
A.B. C.D
(2022·广西河池)如图所示,点,则该反比例函数的解析式为 .
例3
考点2 的几何意义
【解析】∵,∴.∵ 2,∴2.∴.∴,∴.∴该反比例函数的解析式为.
(2022·海南)若反比例函数的图象经过点(2,3),则它的图象也一定经过的点是( )
A.(2,3) B.(3,2)
C.(1,6) D.(6,1)
例4
考点3 求反比例函数解析式
【解析】,故C正确;,故D不正确.故选C.
专项训练
肆
1.(2023·太仓)函数与自变量的部分对应值如表所示,则下列函数表达式中,符合表中对应关系的可能是()
A.B.
C.D.
1 2 4
4 2 1
2.(2023·甘孜)已知点),在反比例函数的图象上,且,则下列结论一定正确的是( )
A.+B.+ C.- D.+
3.(2023·淄博)正在建设中的临滕高速是山东省“十四五”重点建设项目.一段工程施工需要运送的土石方总量为m ,设土石方日平均运送量为(单位:m /天),完成运送任务所需要的时间为(单位:天),则与满足()
A.反比例函数关系 B.正比例函数关系
C.一次函数关系 D.二次函数关系
4.如图所示,反比例函数()的图象与相交,某同学在内做随机扎针实验,针头落在阴影区域内的概率为 .
提升训练
5.(2023·广西)如图所示,过的图象上点,分别作轴,轴的平行线交的图象于,两点,以,为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为,,,,若,则的值为( )
A.4 B.3 C.2 D.1
6.(2024·徐州)如图所示,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点.
(1)求一次函数、反比例函数的表达式;
(2)连接求的面积.
答案
6.解:(1)∵一次函数y=k十b的图象与反比例函数y=的图象相交于点A(-1,n),B(2,1)
∴m=-n=2,
∴m=-2,n=-2,
∴反比例函数解析式为y=,
一次函数y=k十b的图象过A(-1,-2)、B(2,1)
2k+b=1
b=-1
∴一次函数解析式为y=-1
课堂练习
伍
1.(2024·成都)已知点(,)在反比例函数的图象上,则的值为( )
A. B. C. D.
2.(2023·四川)已知点,,均在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
3.近视眼镜的度数(度)与片焦距(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则之间的函数关系式是 .
4.(2024·江阴)杠杆平衡时,“阻力×阻力臂=动力×动力臂”.已知阻力和阻力臂分别为1600和0.5m,动力为(),动力臂为(m).则动力关于动力臂的函数表达式为 .
5.(2024·山西)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度(m/s)是载重后总质量(kg)的反比例函数.已知一款机器狗载重后总质量60kg时,它的最快移动速度6m/s;当其载重后总质量90kg时,它的最快移动速度 m/s
6.(2024·福州)如图,在平面直角坐标系中,反比例函数的图象与交于两点,且点都在第一象限.若(1,2),则点的坐标为 .
7.(2022·贵阳)如图所示,在平面直角坐标系中,等腰直角三角形的斜边轴于点,直角顶点在轴经过上,双曲线边的中点,若,则 .
8.(2024·长春)已知蓄电池电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的解析式(不要求写出自变量的取值范围).
(2)当电阻为3Ω时,求此时的电流.
答案
8.解:(1)设I=
由题意得:U=RI=9X4=36,
∴这个反比例函数的解析式为I=
(2)电阻R为3 时,I=12(A)。
9.(2024·东莞)一个人的脚印信息往往对应着这个人某些方面的基本特征. 某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高之间近似存在一个函数关系,部分数据如下表所示:
脚长(cm) … 23 24 25 26 27 28 …
身高y(cm) … 156 163 170 177 184 191 …
(1)在图1中描出表中数据对应的点;
(2)根据表中数据,从和中选择一个函数模型,它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出的取值范围);
(3)如图2,某场所发现了一个人的脚印,脚长约为25.8cm,请根据(2)中求出的函数解析式,估计这个人的身高.
答案
答案
(2)∵y=(k≠0)转化为k=y=23×156≠24×163≠25×170≠…
∴y与x的函数不可能是y=
故选一次函数y=a+b(a≠0),将点(23,156)、(24,163)代人解析式得:
解得
一次函数解析式为y=7—5。
(3)当x=25.8时,y=7×25.8—5=175.6(cmm)。
答:脚长约为25.8 cm,估计这个人的身高为175.6
-5
谢谢观看
同课章节目录
