第11章 单元测试卷 平面直角坐标系 2024-2025学年沪科版八年级数学上册(含答案)
文档属性
| 名称 | 第11章 单元测试卷 平面直角坐标系 2024-2025学年沪科版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 345.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 00:00:00 | ||
图片预览


文档简介
数学八年级上册第11章 平面直角坐标系
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在平面直角坐标系中,点P(-2,1)所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,象棋盘上,若“将”位于点(3,-2),“车”位于点(-1,-2),则“马”位于
A.(6,1)
B.(5,3)
C.(1,3)
D.(8,2)
3.若点N在第二象限,且到x轴的距离是1,到y轴的距离是3,则点N的坐标是
A.(3,1) B.(-3,-1)
C.(-1,3) D.(-3,1)
4.若点P(m-2,-1-3m)落在坐标轴上,则m的值是
A.m=2 B.m=-
C.m=2或m=- D.m=-2或m=
5.甲、乙、丙三人在看地图时,对四个地标作了如下描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到博物馆.
丙:博物馆在体育馆正西方向200米处.
根据三人的描述,若从图书馆出发,其终点是体育馆,则下列选项正确的是
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走600米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
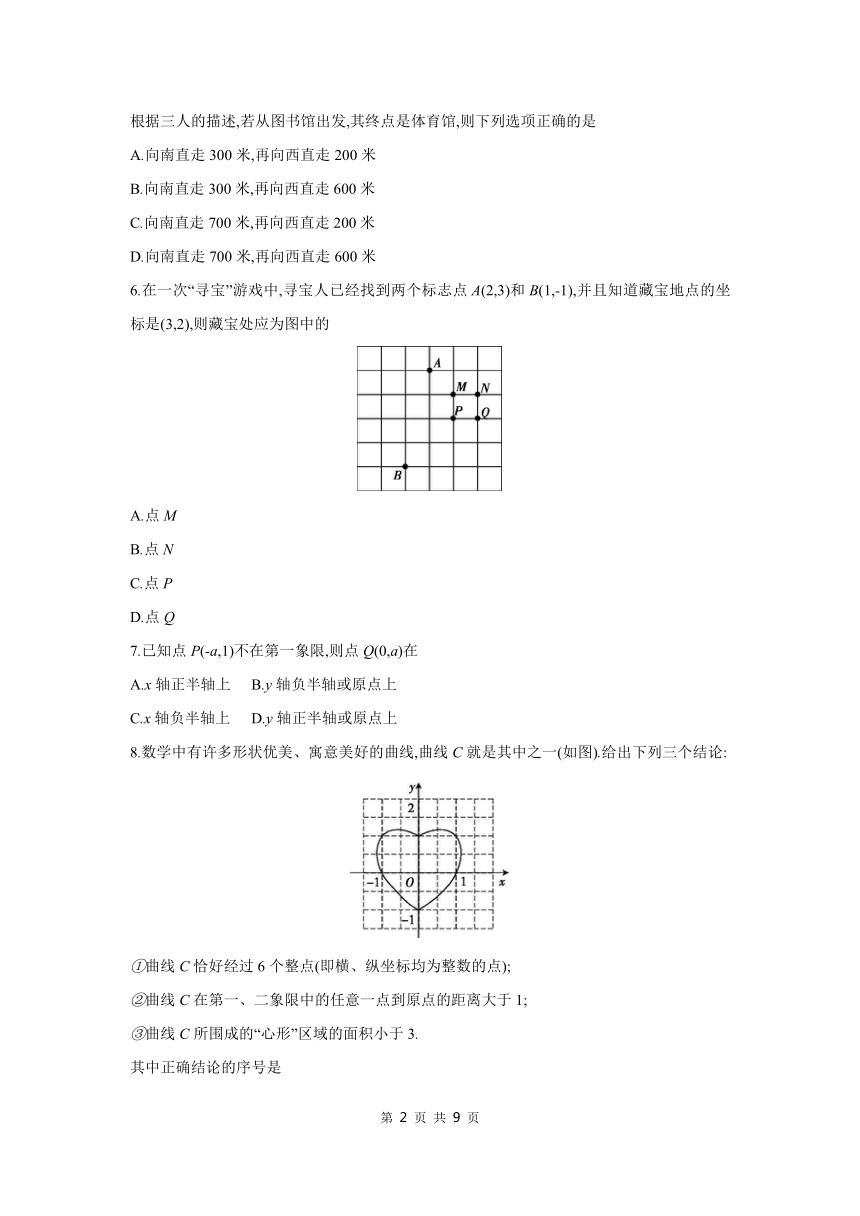
6.在一次“寻宝”游戏中,寻宝人已经找到两个标志点A(2,3)和B(1,-1),并且知道藏宝地点的坐标是(3,2),则藏宝处应为图中的
A.点M
B.点N
C.点P
D.点Q
7.已知点P(-a,1)不在第一象限,则点Q(0,a)在
A.x轴正半轴上 B.y轴负半轴或原点上
C.x轴负半轴上 D.y轴正半轴或原点上
8.数学中有许多形状优美、寓意美好的曲线,曲线C就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C在第一、二象限中的任意一点到原点的距离大于1;
③曲线C所围成的“心形”区域的面积小于3.
其中正确结论的序号是
A.① B.②
C.①② D.①②③
9.在平面直角坐标系中,点A的坐标为(-2,3),若线段AB∥y轴,且AB的长为4,则点B的坐标为
A.(-2,-1) B.(-2,7)
C.(-2,-1)或(-2,7) D.(2,3)
10.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,第一次移动到A1,第二次移动到A2,…,第n次移动到An,则三角形OA2A2023的面积是
A.505 B. C. D.1011
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在平面直角坐标系中,将点P(3,1)向上平移 个单位长度后得到点Q(3,3).
12.若(x-y-1)2+|3x+2y-1|=0,则点P(x,y)在第 象限.
13.已知点A(3,4),B(-1,-2),将线段AB平移到线段CD,点A平移到点C,若平移后点C,D恰好都在坐标轴上,则点C的坐标为 .
14.在平面直角坐标系中,A(0,1),B(2,0),C(4,3),连接AB,BC,AC.
(1)△ABC的面积为 .
(2)P是x轴正半轴上一点,且△ABP与△ABC的面积相等,则点P的坐标为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知点M(3|a|-9,4-2a)在y轴的负半轴上,求代数式(2-a)2023+1的值.
16.在下面的平面直角坐标系中,完成下列各题:
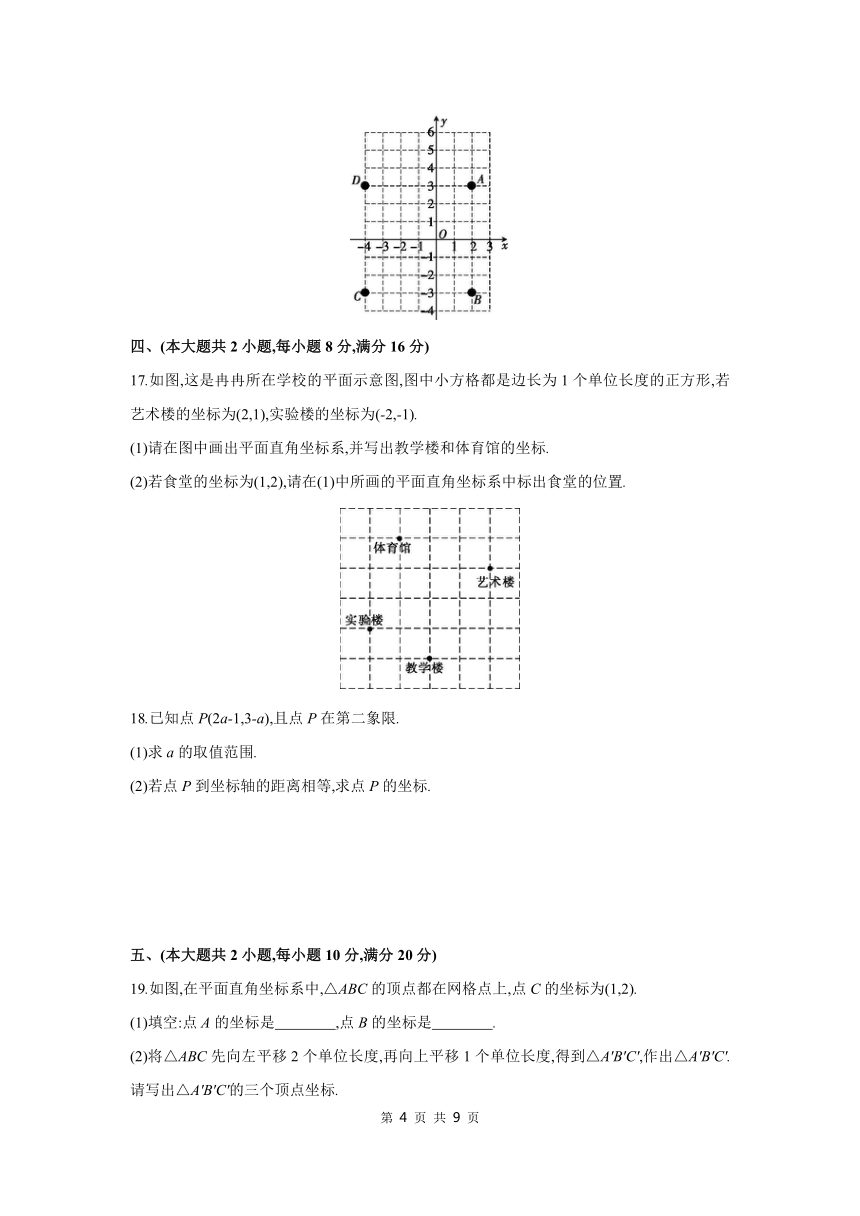
(1)写出图中A,B,C,D各点的坐标,顺次连接A,B,C,D各点,围成的封闭图形是什么图形
(2)描出点E(1,0),F(-1,3),G(-3,0),H(-1,-3),并顺次连接E,F,G,H.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,这是冉冉所在学校的平面示意图,图中小方格都是边长为1个单位长度的正方形,若艺术楼的坐标为(2,1),实验楼的坐标为(-2,-1).
(1)请在图中画出平面直角坐标系,并写出教学楼和体育馆的坐标.
(2)若食堂的坐标为(1,2),请在(1)中所画的平面直角坐标系中标出食堂的位置.
18.已知点P(2a-1,3-a),且点P在第二象限.
(1)求a的取值范围.
(2)若点P到坐标轴的距离相等,求点P的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,点C的坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 .
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',作出△A'B'C'.请写出△A'B'C'的三个顶点坐标.
(3)求△ABC的面积.
20.在平面直角坐标系中,点P从原点O出发,速度为每秒1个单位长度,且点P只能向上或向右运动,请回答下列问题:
(1)将表格填写完整:
点P出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1),(1,0) 2
2秒 (1,1),(2,0),(0,2) 3
3秒 4
(2)当点P从点O出发11秒时,可得到的整数点的个数是 .
(3)当点P从点O出发 秒时,可得到整数点(28,8).
六、(本题满分12分)
21.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着方格线运动.它从A处出发去看望B,C,D处的其他甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为A→B(+1,+4),从B到A记为B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)A→C( , ),B→C( , ),C→D( , ).
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最少路程.
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置.
七、(本题满分12分)
22.如图,同时将点A(-1,0),B(3,0)向上平移2个单位长度,再向右平移1个单位长度,分别得到对应点C,D,连接AC,BD,CD,得到四边形ABDC.
(1)线段AB与CD的关系是 .
(2)若在y轴上存在点 M,连接MA,MB,使S三角形MAB=S四边形ABDC,求出点M的坐标.
(3)若P是边BD上的一个动点,连接PC,PO,请画出图形,并探究∠CPO、∠DCP、∠BOP之间的数量关系.
八、(本题满分14分)
23.阅读下列材料:
材料1 如果点A(x1,y1),B(x2,y2)关于x轴对称,那么x1=x2,y1=-y2;反过来,如果x1=x2,y1=-y2,那么点A(x1,y1),B(x2,y2)关于x轴对称.
材料2 已知点P(x,y),我们把点Q(x+ay,ax+y)叫做点P(x,y)的“a系联动点”,其中a为常数,且a≠0.例如,点(2,5)的“-3系联动点”是(-13,-1).
解答下列问题:
(1)点(4,-1)关于x轴对称的点的坐标是 ;点(4,-1)的“3系联动点”的坐标是 .
(2)已知点P(x,y)的“3系联动点”是(5,7),求x+y的值.
(3)已知点P(x,y)的“a系联动点”与点P(x,y)的“-a系联动点”关于x轴对称,试说明点P(x,y)一定在x轴上.
参考答案
1.B 2.A 3.D 4.C 5.A 6.A 7.D 8.C 9.C
10.B 提示:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
由题意知,OA4n=2n.
因为2023÷4=505……3,
所以点A2023的横坐标为+2=1012,纵坐标为1,
所以A2A2023=1012-1=1011,
所以三角形OA2A2023的面积为×1×1011=,故选B.
11.2 12.四 13.(0,6)或(4,0) 14.(1)4 (2)(10,0)
15.解:因为M(3|a|-9,4-2a)在y轴的负半轴上,
所以解得a=3, 5分
所以(2-a)2023+1=(2-3)2023+1=-1+1=0. 8分
16.解:(1)由题意得A(2,3),B(2,-3),C(-4,-3),D(-4,3),四边形ABCD是正方形. 5分
(2)如图所示. 8分
17.解:(1)教学楼的坐标为(0,-2),体育馆的坐标为(-1,2). 4分
(2)食堂的位置如图所示. 8分
18.解:(1)∵点P(2a-1,3-a),且点P在第二象限,
∴解得a<. 4分
(2)∵点P到坐标轴的距离相等,
∴2a-1+3-a=0,
解得a=-2,
故2a-1=-5,3-a=5,
故点P的坐标为(-5,5). 8分
19.解:(1)(2,-1);(4,3). 2分
(2)如图,△A'B'C'为所作.A'(0,0),B'(2,4),C'(-1,3). 7分
(3)△ABC的面积=3×4-×2×4-×3×1-×3×1=5. 10分
20.解:(1)(0,3),(1,2),(2,1),(3,0). 4分
(2)12. 7分
(3)36. 10分
21.解:(1)A→C(+3,+4),B→C(+2,0),C→D(+1,-2). 6分
(2)1+4+2+1+2=10. 8分
(3)点P如图所示. 12分
22.解:(1)平行且相等(或AB∥CD,AB=CD). 4分
(2)因为AB=4,CO=2,所以S平行四边形ABDC=AB·CO=4×2=8.
设点M的坐标为(0,m),所以×4×|m|=8,解得m=±4,
所以点M的坐标为(0,4)或(0,-4). 8分
(3)如图,过点P作PE∥AB,由平移的性质得AB∥CD,则PE∥CD,
所以∠DCP=∠CPE,∠BOP=∠OPE,
所以∠CPO=∠CPE+∠OPE=∠DCP+∠BOP. 12分
23.解:(1)(4,1);(1,11). 4分
提示:关于x轴对称的两点的横坐标相等,纵坐标互为相反数;点(4,-1)的“3系联动点”的横坐标是4+3×(-1)=1,纵坐标是3×4+(-1)=11.
(2)根据题意得则4x+4y=12,即x+y的值为3. 8分
(3)点P(x,y)的“a系联动点”是(x+ay,ax+y),
点P(x,y)的“-a系联动点”是(x-ay,-ax+y),
因为它们关于x轴对称,所以即
而a≠0,y=0,这说明点P(x,y)一定在x轴上. 14分
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在平面直角坐标系中,点P(-2,1)所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,象棋盘上,若“将”位于点(3,-2),“车”位于点(-1,-2),则“马”位于
A.(6,1)
B.(5,3)
C.(1,3)
D.(8,2)
3.若点N在第二象限,且到x轴的距离是1,到y轴的距离是3,则点N的坐标是
A.(3,1) B.(-3,-1)
C.(-1,3) D.(-3,1)
4.若点P(m-2,-1-3m)落在坐标轴上,则m的值是
A.m=2 B.m=-
C.m=2或m=- D.m=-2或m=
5.甲、乙、丙三人在看地图时,对四个地标作了如下描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到博物馆.
丙:博物馆在体育馆正西方向200米处.
根据三人的描述,若从图书馆出发,其终点是体育馆,则下列选项正确的是
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走600米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
6.在一次“寻宝”游戏中,寻宝人已经找到两个标志点A(2,3)和B(1,-1),并且知道藏宝地点的坐标是(3,2),则藏宝处应为图中的
A.点M
B.点N
C.点P
D.点Q
7.已知点P(-a,1)不在第一象限,则点Q(0,a)在
A.x轴正半轴上 B.y轴负半轴或原点上
C.x轴负半轴上 D.y轴正半轴或原点上
8.数学中有许多形状优美、寓意美好的曲线,曲线C就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C在第一、二象限中的任意一点到原点的距离大于1;
③曲线C所围成的“心形”区域的面积小于3.
其中正确结论的序号是
A.① B.②
C.①② D.①②③
9.在平面直角坐标系中,点A的坐标为(-2,3),若线段AB∥y轴,且AB的长为4,则点B的坐标为
A.(-2,-1) B.(-2,7)
C.(-2,-1)或(-2,7) D.(2,3)
10.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,第一次移动到A1,第二次移动到A2,…,第n次移动到An,则三角形OA2A2023的面积是
A.505 B. C. D.1011
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在平面直角坐标系中,将点P(3,1)向上平移 个单位长度后得到点Q(3,3).
12.若(x-y-1)2+|3x+2y-1|=0,则点P(x,y)在第 象限.
13.已知点A(3,4),B(-1,-2),将线段AB平移到线段CD,点A平移到点C,若平移后点C,D恰好都在坐标轴上,则点C的坐标为 .
14.在平面直角坐标系中,A(0,1),B(2,0),C(4,3),连接AB,BC,AC.
(1)△ABC的面积为 .
(2)P是x轴正半轴上一点,且△ABP与△ABC的面积相等,则点P的坐标为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知点M(3|a|-9,4-2a)在y轴的负半轴上,求代数式(2-a)2023+1的值.
16.在下面的平面直角坐标系中,完成下列各题:
(1)写出图中A,B,C,D各点的坐标,顺次连接A,B,C,D各点,围成的封闭图形是什么图形
(2)描出点E(1,0),F(-1,3),G(-3,0),H(-1,-3),并顺次连接E,F,G,H.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,这是冉冉所在学校的平面示意图,图中小方格都是边长为1个单位长度的正方形,若艺术楼的坐标为(2,1),实验楼的坐标为(-2,-1).
(1)请在图中画出平面直角坐标系,并写出教学楼和体育馆的坐标.
(2)若食堂的坐标为(1,2),请在(1)中所画的平面直角坐标系中标出食堂的位置.
18.已知点P(2a-1,3-a),且点P在第二象限.
(1)求a的取值范围.
(2)若点P到坐标轴的距离相等,求点P的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,点C的坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 .
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',作出△A'B'C'.请写出△A'B'C'的三个顶点坐标.
(3)求△ABC的面积.
20.在平面直角坐标系中,点P从原点O出发,速度为每秒1个单位长度,且点P只能向上或向右运动,请回答下列问题:
(1)将表格填写完整:
点P出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1),(1,0) 2
2秒 (1,1),(2,0),(0,2) 3
3秒 4
(2)当点P从点O出发11秒时,可得到的整数点的个数是 .
(3)当点P从点O出发 秒时,可得到整数点(28,8).
六、(本题满分12分)
21.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着方格线运动.它从A处出发去看望B,C,D处的其他甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为A→B(+1,+4),从B到A记为B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)A→C( , ),B→C( , ),C→D( , ).
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最少路程.
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置.
七、(本题满分12分)
22.如图,同时将点A(-1,0),B(3,0)向上平移2个单位长度,再向右平移1个单位长度,分别得到对应点C,D,连接AC,BD,CD,得到四边形ABDC.
(1)线段AB与CD的关系是 .
(2)若在y轴上存在点 M,连接MA,MB,使S三角形MAB=S四边形ABDC,求出点M的坐标.
(3)若P是边BD上的一个动点,连接PC,PO,请画出图形,并探究∠CPO、∠DCP、∠BOP之间的数量关系.
八、(本题满分14分)
23.阅读下列材料:
材料1 如果点A(x1,y1),B(x2,y2)关于x轴对称,那么x1=x2,y1=-y2;反过来,如果x1=x2,y1=-y2,那么点A(x1,y1),B(x2,y2)关于x轴对称.
材料2 已知点P(x,y),我们把点Q(x+ay,ax+y)叫做点P(x,y)的“a系联动点”,其中a为常数,且a≠0.例如,点(2,5)的“-3系联动点”是(-13,-1).
解答下列问题:
(1)点(4,-1)关于x轴对称的点的坐标是 ;点(4,-1)的“3系联动点”的坐标是 .
(2)已知点P(x,y)的“3系联动点”是(5,7),求x+y的值.
(3)已知点P(x,y)的“a系联动点”与点P(x,y)的“-a系联动点”关于x轴对称,试说明点P(x,y)一定在x轴上.
参考答案
1.B 2.A 3.D 4.C 5.A 6.A 7.D 8.C 9.C
10.B 提示:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
由题意知,OA4n=2n.
因为2023÷4=505……3,
所以点A2023的横坐标为+2=1012,纵坐标为1,
所以A2A2023=1012-1=1011,
所以三角形OA2A2023的面积为×1×1011=,故选B.
11.2 12.四 13.(0,6)或(4,0) 14.(1)4 (2)(10,0)
15.解:因为M(3|a|-9,4-2a)在y轴的负半轴上,
所以解得a=3, 5分
所以(2-a)2023+1=(2-3)2023+1=-1+1=0. 8分
16.解:(1)由题意得A(2,3),B(2,-3),C(-4,-3),D(-4,3),四边形ABCD是正方形. 5分
(2)如图所示. 8分
17.解:(1)教学楼的坐标为(0,-2),体育馆的坐标为(-1,2). 4分
(2)食堂的位置如图所示. 8分
18.解:(1)∵点P(2a-1,3-a),且点P在第二象限,
∴解得a<. 4分
(2)∵点P到坐标轴的距离相等,
∴2a-1+3-a=0,
解得a=-2,
故2a-1=-5,3-a=5,
故点P的坐标为(-5,5). 8分
19.解:(1)(2,-1);(4,3). 2分
(2)如图,△A'B'C'为所作.A'(0,0),B'(2,4),C'(-1,3). 7分
(3)△ABC的面积=3×4-×2×4-×3×1-×3×1=5. 10分
20.解:(1)(0,3),(1,2),(2,1),(3,0). 4分
(2)12. 7分
(3)36. 10分
21.解:(1)A→C(+3,+4),B→C(+2,0),C→D(+1,-2). 6分
(2)1+4+2+1+2=10. 8分
(3)点P如图所示. 12分
22.解:(1)平行且相等(或AB∥CD,AB=CD). 4分
(2)因为AB=4,CO=2,所以S平行四边形ABDC=AB·CO=4×2=8.
设点M的坐标为(0,m),所以×4×|m|=8,解得m=±4,
所以点M的坐标为(0,4)或(0,-4). 8分
(3)如图,过点P作PE∥AB,由平移的性质得AB∥CD,则PE∥CD,
所以∠DCP=∠CPE,∠BOP=∠OPE,
所以∠CPO=∠CPE+∠OPE=∠DCP+∠BOP. 12分
23.解:(1)(4,1);(1,11). 4分
提示:关于x轴对称的两点的横坐标相等,纵坐标互为相反数;点(4,-1)的“3系联动点”的横坐标是4+3×(-1)=1,纵坐标是3×4+(-1)=11.
(2)根据题意得则4x+4y=12,即x+y的值为3. 8分
(3)点P(x,y)的“a系联动点”是(x+ay,ax+y),
点P(x,y)的“-a系联动点”是(x-ay,-ax+y),
因为它们关于x轴对称,所以即
而a≠0,y=0,这说明点P(x,y)一定在x轴上. 14分
