期末模拟卷(含答案)2024-2025学年沪科版八年级数学上册
文档属性
| 名称 | 期末模拟卷(含答案)2024-2025学年沪科版八年级数学上册 | 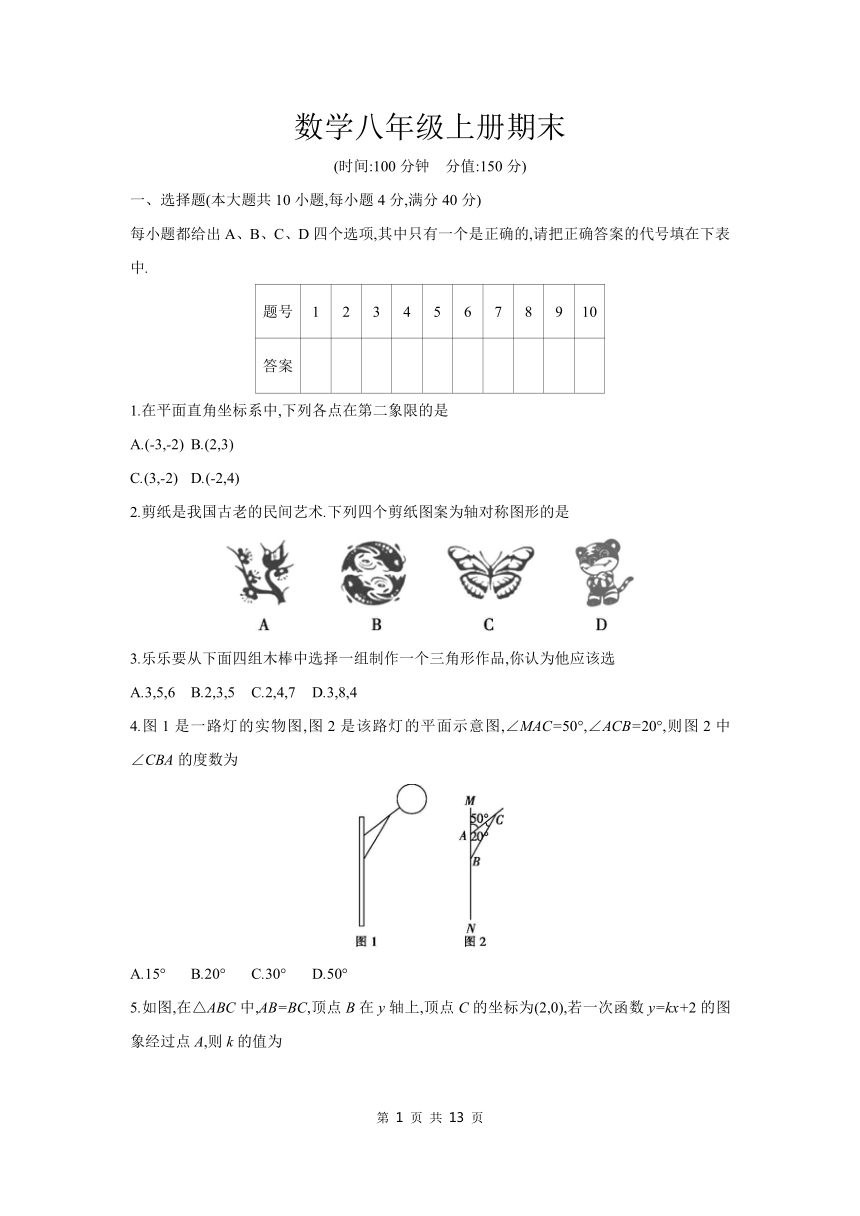 | |
| 格式 | docx | ||
| 文件大小 | 310.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 15:05:57 | ||
图片预览




文档简介
数学八年级上册期末
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在平面直角坐标系中,下列各点在第二象限的是
A.(-3,-2) B.(2,3)
C.(3,-2) D.(-2,4)
2.剪纸是我国古老的民间艺术.下列四个剪纸图案为轴对称图形的是
3.乐乐要从下面四组木棒中选择一组制作一个三角形作品,你认为他应该选
A.3,5,6 B.2,3,5 C.2,4,7 D.3,8,4
4.图1是一路灯的实物图,图2是该路灯的平面示意图,∠MAC=50°,∠ACB=20°,则图2中∠CBA的度数为
A.15° B.20° C.30° D.50°
5.如图,在△ABC中,AB=BC,顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A,则k的值为
A. B.-
C.1 D.-1
6.小明把一副含有45°,30°角的直角三角板如图所示摆放,使得AC和DE垂直交于点F,AD与BC交于点G,则∠AGB的度数为
A.80° B.75°
C.70° D.60°
7.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,须补充的条件是
A.∠B=∠C
B.∠D=∠E
C.∠1=∠2
D.∠CAD=∠DAC
8.如图,在△ABC中,EF∥BC,∠BAC的平分线交BC于点D,若∠ADC=80°,∠ACH=115°,则∠AEF的度数为
A.40°
B.45°
C.50°
D.55°
9.如图,在等边三角形ABC中,M、N是边BC上的动点,MN=BC,D、E分别是边AB、AC上的点,且DM⊥BC,EN⊥BC,垂足分别为M、N,则AD+AE的值
A.保持不变
B.先变小后变大
C.先变大后变小
D.一直变大
10.在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°,且CD=CA=AB,则y与x之间不可能存在的关系式是
A.y=90-x B.y=x-90
C.y=180-x D.y=120-x
二、填空题(本大题共4小题,每小题5分,满分20分)
11.命题:“同角或等角的补角相等”的逆命题是 .
12.在平面直角坐标系中,点P(x-2,x+4)不可能在第 象限.
13.如图,在平面直角坐标系中,△ABC是等腰直角三角形,AC=BC.已知点A(0,3),点B(-9,0),则点C的坐标为 .
14.如图,在△ABC中,DM、EN分别垂直平分边AC和边BC,交边AB于M、N两点,DM与EN相交于点F.
(1)若AB=3 cm,则△CMN的周长为 .
(2)若∠MFN=70°,则∠MCN的度数为 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,∠C=∠E,AC=AE,点D在BC边上,∠1=∠2,AC和DE相交于点O.求证:△ABC≌△ADE.
16.判断下列命题的真假,是假命题的用举反例的方法说明.
(1)若a,b是无理数,则a+b是无理数.
(2)全等三角形的面积相等.
四、(本大题共2小题,每小题8分,满分16分)
17.已知点P(5-m,6-3m)在平面直角坐标系内.
(1)若点P在第四象限,求m的取值范围.
(2)若点P在坐标轴上,求m的值.
18.如图,秤是我国传统的计重工具,方便了人们的生活,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的质量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米),秤钩所挂物体的质量为y(千克),则y是x的一次函数.若干次称重时所记录的一些数据如下表.
x(厘米) 1 2 4 7 11 12
y(千克) 0.75 1.00 1.50 2.25 3.25 3.50
(1)求y与x之间的函数关系式.
(2)当秤杆上秤砣到秤纽的水平距离为14厘米时,秤钩所挂物体的质量是多少千克
(3)当秤钩所挂物体的质量为4.50千克时,秤杆上秤砣到秤纽的水平距离是多少厘米
五、(本大题共2小题,每小题10分,满分20分)
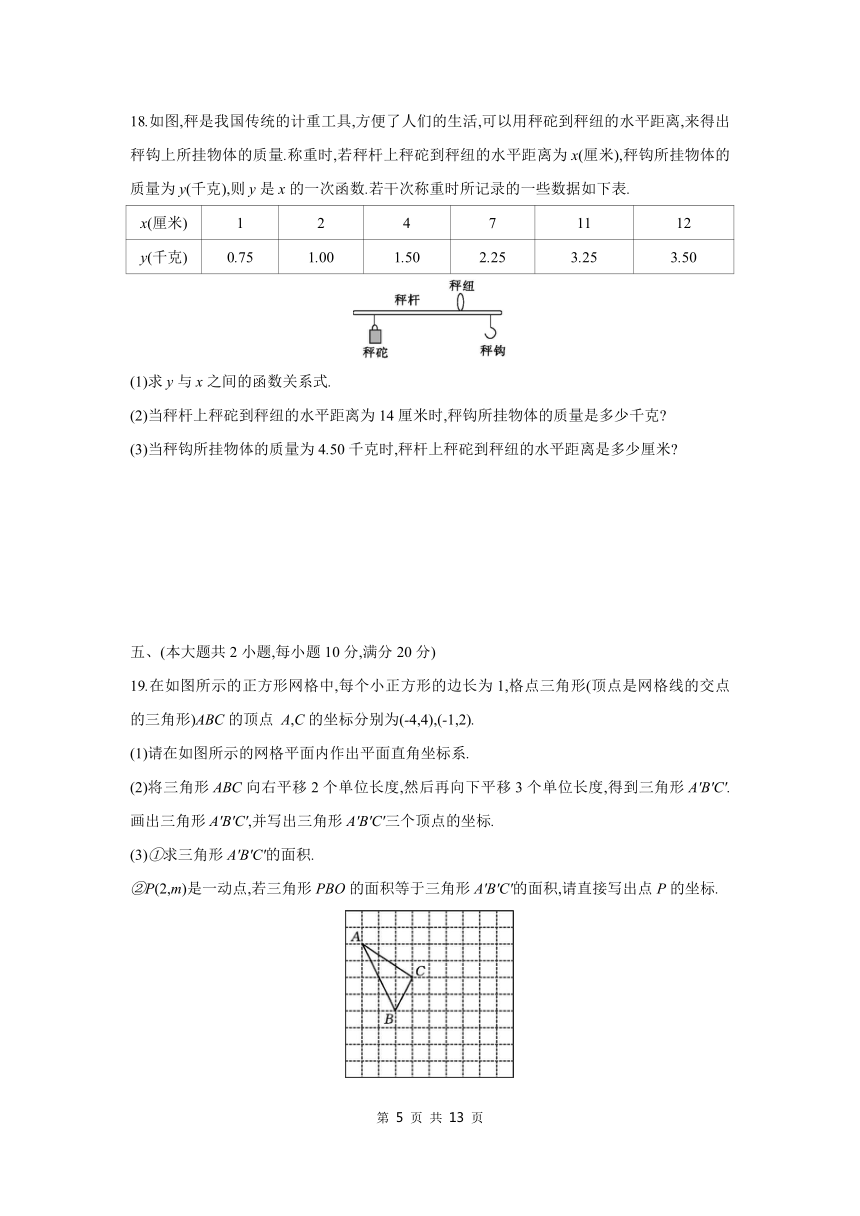
19.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点 A,C的坐标分别为(-4,4),(-1,2).
(1)请在如图所示的网格平面内作出平面直角坐标系.
(2)将三角形ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到三角形A'B'C'.画出三角形A'B'C',并写出三角形A'B'C'三个顶点的坐标.
(3)①求三角形A'B'C'的面积.
②P(2,m)是一动点,若三角形PBO的面积等于三角形A'B'C'的面积,请直接写出点P的坐标.
20.如图,直线l1:y1=2x+1与坐标轴交于A,C两点,直线l2:y2=-x-2与坐标轴交于B,D两点,两直线的交点为点P.
(1)求C,D两点的坐标.
(2)求△DCP的面积.
(3)当y1>y2时,求自变量x的取值范围.
六、(本题满分12分)
21.某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)A,B两种奖品的单价各是多少元
(2)学校计划购买A,B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元.写出W(元)与m(件)的函数关系式,求出自变量m的取值范围,并确定最少费用W的值.
七、(本题满分12分)
22.如图,△ABC和△ADE都是等腰直角三角形,BC和DE分别是其斜边,连接BE,CD交于点O,连接OA.
(1)求证:△BAE≌△CAD.
(2)求证:BE⊥CD.
(3)问OA是∠BOD的平分线吗 请说明理由.
八、(本题满分14分)
23.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,交CB的延长线于点F.
(1)求证:△ABC≌△ADE.
(2)求∠FAE的度数.
(3)求证:CD=2BF+DE.
参考答案
1.D 2.C 3.A 4.C 5.C 6.B 7.C 8.B 9.A
10.D 提示:如图1,当点D在线段BC上时,
∵∠ABC=x°,CA=AB,
∴∠C=∠ABC=x°.
∵CD=CA,
∴∠ADC=∠CAD==90°-x°.
∵∠ADC=∠B+∠BAD,
∴90-x=x+y,即y=90-x.
如图2,当点D在线段BC的延长线上时.
同理可得y=180-x.
如图3,当点D在线段CB的延长线上时,
同理可得y=x-90.
故选D.
11.如果两个角的补角相等,那么这两个角相等或为同一个角
12.四 13.(-6,6) 14.(1)3 cm (2)40°
15.证明:∵∠ADC=∠1+∠B,
即∠ADE+∠2=∠1+∠B.
∵∠1=∠2,
∴∠ADE=∠B. 4分
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS). 8分
16.解: (1)假命题.反例:若a=2+,b=2-,则a+b=4,是有理数. 5分
(2)真命题. 8分
17.解:(1)根据题意,若点P在第四象限,
可得
解得2(2)根据题意,若点P在坐标轴上,
当点P(5-m,6-3m)在x轴上时,有6-3m=0,解得m=2,
当点P(5-m,6-3m)在y轴上,有5-m=0,解得m=5,
综上所述,m的值为2或5. 8分
18.解:(1)依题意,设y与x之间的函数关系式为y=kx+b(k≠0),
把x=1,y=0.75,x=2,y=1代入,
可得解得
∴y与x之间的函数关系式是y=x+. 4分
(2)当x=14时,y=×14+=4,
∴秤杆上秤砣到秤纽的水平距离为14厘米时,秤钩所挂物体的质量是4千克. 6分
(3)当y=4.50时,x+=4.50,
解得x=16,
∴当秤钩所挂物体的质量为4.50千克时,秤杆上秤砣到秤纽的水平距离是16厘米. 8分
19.解:(1)如图,建立平面直角坐标系. 3分
(2)如图,△A'B'C'为所求,A'(-2,1),B'(0,-3),C'(1,-1). 6分
(3)①S△A'B'C'=3×4-×2×1-×2×3-×2×4=4. 8分
②P(2,4)或(2,-4). 10分
20.解:(1)令y1=0,得0=2x+1,解得x=-,
令y2=0,得0=-x-2,解得x=-2,
∴C(-,0),D(-2,0). 4分
(2)由解得
所以P(-1,-1),
则S△DCP=×(-+2)×1=. 8分
(3)由图象可知:当y1>y2时,x的取值范围是x>-1. 10分
21.解:(1)设A种奖品的单价是x元,B种奖品的单价是y元.
由题意,得解得
答:A种奖品的单价是10元,B种奖品的单价是15元. 6分
(2)由题意,得W=10m+15(100-m)=-5m+1500,
∴解得70≤m≤75.
∵m是整数,∴m=70,71,72,73,74,75.
∵W=-5m+1500,-5<0,
∴W随m的增大而减小,
∴当m=75时,W最小=1125,
∴应买A种奖品75件,B种奖品25件,才能使总费用最少,最少费用为1125元. 12分
22.解:(1)证明:∵△ABC和△ADE都是等腰直角三角形,
∴∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD,
∴△BAE≌△CAD(SAS). 4分
(2)证明:∵△BAE≌△CAD,
∴∠ABO=∠ACO,
∴∠OBC+∠OCB=∠ABC+∠ACB=90°,
∴∠BOC=90°,即BE⊥CD. 7分
(3)OA是∠BOD的平分线.
理由:如图,过点A分别作AG⊥BE,AH⊥CD,垂足分别为G,H. 8分
∵△BAE≌△CAD,
∴S△BAE=S△CAD,且BE=CD,
∴AG=AH,
∴OA平分∠BOD. 12分
23.解: (1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS). 4分
(2)∵∠CAE=90°,AC=AE,∴∠E=45°.
由(1)知△ABC≌△ADE,
∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠CAF+∠CAE=45°+90°=135°. 7分
(3)证明:如图,延长BF到点G,使得FG=FB,连接AG.
∵AF⊥BC,∴∠AFG=∠AFB=90°.
在△AFB和△AFG中,
∴△AFB≌△AFG(SAS), 10分
∴AB=AG,∠ABF=∠G.
∵AB=AD,∴AG=AD.
∵△ABC≌△ADE,
∴∠CBA=∠EDA,CB=ED,
∴∠ABF=∠CDA,
∴∠G=∠CDA.
由题意易得∠GCA=∠DCA=45°,∴∠CAG=∠CAD.
在△CGA和△CDA中,
∴△CGA≌△CDA(ASA),
∴CG=CD.
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE. 14分
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在平面直角坐标系中,下列各点在第二象限的是
A.(-3,-2) B.(2,3)
C.(3,-2) D.(-2,4)
2.剪纸是我国古老的民间艺术.下列四个剪纸图案为轴对称图形的是
3.乐乐要从下面四组木棒中选择一组制作一个三角形作品,你认为他应该选
A.3,5,6 B.2,3,5 C.2,4,7 D.3,8,4
4.图1是一路灯的实物图,图2是该路灯的平面示意图,∠MAC=50°,∠ACB=20°,则图2中∠CBA的度数为
A.15° B.20° C.30° D.50°
5.如图,在△ABC中,AB=BC,顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A,则k的值为
A. B.-
C.1 D.-1
6.小明把一副含有45°,30°角的直角三角板如图所示摆放,使得AC和DE垂直交于点F,AD与BC交于点G,则∠AGB的度数为
A.80° B.75°
C.70° D.60°
7.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,须补充的条件是
A.∠B=∠C
B.∠D=∠E
C.∠1=∠2
D.∠CAD=∠DAC
8.如图,在△ABC中,EF∥BC,∠BAC的平分线交BC于点D,若∠ADC=80°,∠ACH=115°,则∠AEF的度数为
A.40°
B.45°
C.50°
D.55°
9.如图,在等边三角形ABC中,M、N是边BC上的动点,MN=BC,D、E分别是边AB、AC上的点,且DM⊥BC,EN⊥BC,垂足分别为M、N,则AD+AE的值
A.保持不变
B.先变小后变大
C.先变大后变小
D.一直变大
10.在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°,且CD=CA=AB,则y与x之间不可能存在的关系式是
A.y=90-x B.y=x-90
C.y=180-x D.y=120-x
二、填空题(本大题共4小题,每小题5分,满分20分)
11.命题:“同角或等角的补角相等”的逆命题是 .
12.在平面直角坐标系中,点P(x-2,x+4)不可能在第 象限.
13.如图,在平面直角坐标系中,△ABC是等腰直角三角形,AC=BC.已知点A(0,3),点B(-9,0),则点C的坐标为 .
14.如图,在△ABC中,DM、EN分别垂直平分边AC和边BC,交边AB于M、N两点,DM与EN相交于点F.
(1)若AB=3 cm,则△CMN的周长为 .
(2)若∠MFN=70°,则∠MCN的度数为 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,∠C=∠E,AC=AE,点D在BC边上,∠1=∠2,AC和DE相交于点O.求证:△ABC≌△ADE.
16.判断下列命题的真假,是假命题的用举反例的方法说明.
(1)若a,b是无理数,则a+b是无理数.
(2)全等三角形的面积相等.
四、(本大题共2小题,每小题8分,满分16分)
17.已知点P(5-m,6-3m)在平面直角坐标系内.
(1)若点P在第四象限,求m的取值范围.
(2)若点P在坐标轴上,求m的值.
18.如图,秤是我国传统的计重工具,方便了人们的生活,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的质量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米),秤钩所挂物体的质量为y(千克),则y是x的一次函数.若干次称重时所记录的一些数据如下表.
x(厘米) 1 2 4 7 11 12
y(千克) 0.75 1.00 1.50 2.25 3.25 3.50
(1)求y与x之间的函数关系式.
(2)当秤杆上秤砣到秤纽的水平距离为14厘米时,秤钩所挂物体的质量是多少千克
(3)当秤钩所挂物体的质量为4.50千克时,秤杆上秤砣到秤纽的水平距离是多少厘米
五、(本大题共2小题,每小题10分,满分20分)
19.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点 A,C的坐标分别为(-4,4),(-1,2).
(1)请在如图所示的网格平面内作出平面直角坐标系.
(2)将三角形ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到三角形A'B'C'.画出三角形A'B'C',并写出三角形A'B'C'三个顶点的坐标.
(3)①求三角形A'B'C'的面积.
②P(2,m)是一动点,若三角形PBO的面积等于三角形A'B'C'的面积,请直接写出点P的坐标.
20.如图,直线l1:y1=2x+1与坐标轴交于A,C两点,直线l2:y2=-x-2与坐标轴交于B,D两点,两直线的交点为点P.
(1)求C,D两点的坐标.
(2)求△DCP的面积.
(3)当y1>y2时,求自变量x的取值范围.
六、(本题满分12分)
21.某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)A,B两种奖品的单价各是多少元
(2)学校计划购买A,B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元.写出W(元)与m(件)的函数关系式,求出自变量m的取值范围,并确定最少费用W的值.
七、(本题满分12分)
22.如图,△ABC和△ADE都是等腰直角三角形,BC和DE分别是其斜边,连接BE,CD交于点O,连接OA.
(1)求证:△BAE≌△CAD.
(2)求证:BE⊥CD.
(3)问OA是∠BOD的平分线吗 请说明理由.
八、(本题满分14分)
23.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,交CB的延长线于点F.
(1)求证:△ABC≌△ADE.
(2)求∠FAE的度数.
(3)求证:CD=2BF+DE.
参考答案
1.D 2.C 3.A 4.C 5.C 6.B 7.C 8.B 9.A
10.D 提示:如图1,当点D在线段BC上时,
∵∠ABC=x°,CA=AB,
∴∠C=∠ABC=x°.
∵CD=CA,
∴∠ADC=∠CAD==90°-x°.
∵∠ADC=∠B+∠BAD,
∴90-x=x+y,即y=90-x.
如图2,当点D在线段BC的延长线上时.
同理可得y=180-x.
如图3,当点D在线段CB的延长线上时,
同理可得y=x-90.
故选D.
11.如果两个角的补角相等,那么这两个角相等或为同一个角
12.四 13.(-6,6) 14.(1)3 cm (2)40°
15.证明:∵∠ADC=∠1+∠B,
即∠ADE+∠2=∠1+∠B.
∵∠1=∠2,
∴∠ADE=∠B. 4分
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS). 8分
16.解: (1)假命题.反例:若a=2+,b=2-,则a+b=4,是有理数. 5分
(2)真命题. 8分
17.解:(1)根据题意,若点P在第四象限,
可得
解得2
当点P(5-m,6-3m)在x轴上时,有6-3m=0,解得m=2,
当点P(5-m,6-3m)在y轴上,有5-m=0,解得m=5,
综上所述,m的值为2或5. 8分
18.解:(1)依题意,设y与x之间的函数关系式为y=kx+b(k≠0),
把x=1,y=0.75,x=2,y=1代入,
可得解得
∴y与x之间的函数关系式是y=x+. 4分
(2)当x=14时,y=×14+=4,
∴秤杆上秤砣到秤纽的水平距离为14厘米时,秤钩所挂物体的质量是4千克. 6分
(3)当y=4.50时,x+=4.50,
解得x=16,
∴当秤钩所挂物体的质量为4.50千克时,秤杆上秤砣到秤纽的水平距离是16厘米. 8分
19.解:(1)如图,建立平面直角坐标系. 3分
(2)如图,△A'B'C'为所求,A'(-2,1),B'(0,-3),C'(1,-1). 6分
(3)①S△A'B'C'=3×4-×2×1-×2×3-×2×4=4. 8分
②P(2,4)或(2,-4). 10分
20.解:(1)令y1=0,得0=2x+1,解得x=-,
令y2=0,得0=-x-2,解得x=-2,
∴C(-,0),D(-2,0). 4分
(2)由解得
所以P(-1,-1),
则S△DCP=×(-+2)×1=. 8分
(3)由图象可知:当y1>y2时,x的取值范围是x>-1. 10分
21.解:(1)设A种奖品的单价是x元,B种奖品的单价是y元.
由题意,得解得
答:A种奖品的单价是10元,B种奖品的单价是15元. 6分
(2)由题意,得W=10m+15(100-m)=-5m+1500,
∴解得70≤m≤75.
∵m是整数,∴m=70,71,72,73,74,75.
∵W=-5m+1500,-5<0,
∴W随m的增大而减小,
∴当m=75时,W最小=1125,
∴应买A种奖品75件,B种奖品25件,才能使总费用最少,最少费用为1125元. 12分
22.解:(1)证明:∵△ABC和△ADE都是等腰直角三角形,
∴∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD,
∴△BAE≌△CAD(SAS). 4分
(2)证明:∵△BAE≌△CAD,
∴∠ABO=∠ACO,
∴∠OBC+∠OCB=∠ABC+∠ACB=90°,
∴∠BOC=90°,即BE⊥CD. 7分
(3)OA是∠BOD的平分线.
理由:如图,过点A分别作AG⊥BE,AH⊥CD,垂足分别为G,H. 8分
∵△BAE≌△CAD,
∴S△BAE=S△CAD,且BE=CD,
∴AG=AH,
∴OA平分∠BOD. 12分
23.解: (1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS). 4分
(2)∵∠CAE=90°,AC=AE,∴∠E=45°.
由(1)知△ABC≌△ADE,
∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠CAF+∠CAE=45°+90°=135°. 7分
(3)证明:如图,延长BF到点G,使得FG=FB,连接AG.
∵AF⊥BC,∴∠AFG=∠AFB=90°.
在△AFB和△AFG中,
∴△AFB≌△AFG(SAS), 10分
∴AB=AG,∠ABF=∠G.
∵AB=AD,∴AG=AD.
∵△ABC≌△ADE,
∴∠CBA=∠EDA,CB=ED,
∴∠ABF=∠CDA,
∴∠G=∠CDA.
由题意易得∠GCA=∠DCA=45°,∴∠CAG=∠CAD.
在△CGA和△CDA中,
∴△CGA≌△CDA(ASA),
∴CG=CD.
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE. 14分
同课章节目录
